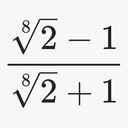ζ(s,∙∙∙,s)の一般項
定義
$\bm s:1\to m \Defarrow \bm s \coloneqq
(s_1,\range s2m)$
$a\vbin<\bm x_{[1\to m]} \Defarrow a< x_1< x_2<\cdots< x_m$\mathbin{{#1}\!\llap|\ }で表示できる。
$\displaystyle \prod_{1\to m} \bm n^{-\bm s} \coloneqq
\prod_{k=1}^m n_k^{-s_k}$
$\beginend{align}{ S_m(s,t) \acoloneqq \sum_{k=0}^m \zeta{\qty(\{s\}^k,t,\{s\}^{m-k})} \\ S^\star_m(s,t) \acoloneqq \sum_{k=0}^m \zeta^\star{\qty(\{s\}^k,t,\{s\}^{m-k})} }$
定理
$\beginend{alignat}{2 &S_m(s,t) = \zeta{\qty(\{s\}^m)}\zeta(t) &&- S_{m-1}(s,s+t) \\ &S^\star_m(s,t) = \zeta^\star{\qty(\{s\}^m)}\zeta(t) &&+ S^\star_{m-1}(s,s+t) }$
$\beginend{alignat}{2 &\zeta{\qty(\{s\}^m)} &&= \sum_{j=1}^m (-1)^{m-j} &&\sum_{0=\vbin<\bm k_{[0\to j]}=m} \prod_{l=1}^j \frac{\zeta((k_l-k_{l-1})s)}{k_l} \\ &\zeta^\star{\qty(\{s\}^m)} &&= \sum_{j=1}^m &&\sum_{0=\vbin<\bm k_{[0\to j]}=m} \prod_{l=1}^j \frac{\zeta((k_l-k_{l-1})s)}{k_l} }$
1行目
$\beginend{align}{ \sahen &= \frac{S_{m-1}(s,s)}m \\&= \frac1m\sum_{n=1}^m (-1)^{n-1}\zeta(ns)\zeta{\qty(\{s\}^{m-n})} \quad\because\textsf{補題1} \\&= \frac1m\sum_{n=0}^{m-1} (-1)^{m-1-n}\zeta((m-n)s)\zeta{\qty(\{s\}^n)} \\&= \frac{(-1)^{m-1}}m\qty[\zeta(ms) + \sum_{0< n< m} (-1)^n\zeta((m-n)s)\zeta{\qty(\{s\}^n)}] \\&= \frac{(-1)^{m-1}}m\qty(\zeta{(ms)} - \sum_{0< n_1< m} \frac{\zeta((m-n_1)s)}{n_1}\qty(\zeta{(n_1s)} - \sum_{0< n_2< n_1} \frac{\zeta((n_1-n_2)s)}{n_2}\qty(\zeta{(n_2s)} - \sum_{0< n_3< n_2} \frac{\zeta((n_2-n_3)s)}{n_3}\Bigg(\cdots\Bigg)))) \\&= \uhen }$
2行目
$S^\star_m(s,t)$の漸化式は$S_m(s,t)
$のものと比較して第2項の符号が$+$である為、
$-$が生じず、それ以外は1行目と同じである。
一般化
$\bm f:1\to m$
$\beginend{alignat}{3
&G(\bm f) &\acoloneqq
\sum_{-1\vbin<\bm n_{[1\to m]}} \prod \bm f(\bm n)\\
&G^\star(\bm f) &\acoloneqq
\sum_{0\vbin\le\bm n_{[1\to m]}} \prod \bm f(\bm n)
}$
$\beginend{alignat}{2
&G{\qty(\{f\}^m)} &&=
\sum_{j=1}^m (-1)^{m-j} &&\sum_{0=\vbin<\bm k_{[0\to j]}=m}
\prod_{l=1}^j \frac{G{\qty(f^{k_l-k_{l-1}})}}{k_l} \\
&G^\star{\qty(\{f\}^m)} &&=
\sum_{j=1}^m &&\sum_{0=\vbin<\bm k_{[0\to j]}=m}
\prod_{l=1}^j \frac{G{\qty(f^{k_l-k_{l-1}})}}{k_l}
}$
これは本題の左辺を交項級数等の類似物に置き換えても展開できることを意味します。
表
$\displaystyle H^\pm_m(f) \coloneqq
\sum_{j=1}^m (\pm1)^{m-j} \sum_{0=\vbin<\bm k_{[0\to j]}=m}
\prod_{l=1}^j \frac{G{\qty(f^{k_l-k_{l-1}})}}{k_l}$
$G{\qty(\{f\}^m)}=H^-_m(f),
G^\star{\qty(\{f\}^m)}=H^+_m(f)$
| $m$ | $m!H^\pm_m(f)$ |
|---|---|
| $1$ | $G(f)$ |
| $2$ | $G(f)^2 \pm G{\qty(f^2)}$ |
| $3$ | $G(f)^3 \pm3G(f)G{\qty(f^2)} +2G{\qty(f^3)}$ |
| $4$ | $G(f)^4 \pm6G(f)^2G{\qty(f^2)} + 8G(f)G{\qty(f^3)} +3G{\qty(f^2)}^2 \pm6G{\qty(f^4)}$ |