保型形式入門:Γ\ℍの複素構造
はじめに
この記事では 前回の記事 に引き続き保型形式の基礎理論について要所を掻い摘んで解説していきます。
$\G\backslash\H^*$の成すリーマン面
この記事では$\G\backslash\H^*$にリーマン面の構造を入れていく。
位相空間$X$とその開集合$U_\la$上の写像$\varphi_\la:U_\la\to\C$が
・$X$は連結なハウスドルフ空間
・$\{U_\la\}_{\la\in\La}$は$X$の被覆、つまり$X=\bigcup_{\la\in\La}U_\la$
・$\varphi_\la:U_\la\to\varphi_\la(U_\la)$は同相写像
・$U_\a\cap U_\b\neq\emptyset$なら$\varphi_\a\circ\varphi_\b^{-1}:\varphi_\a(U_\a\cap U_\b)\to\varphi_\b(U_\a\cap U_\b)$は正則関数
を満たすとき、$(X,\{(U_\la,\varphi_\la)\}_{\la\in\La})$はリーマン面、あるいは単に$X$はリーマン面であるという。
この各写像$\varphi_\la$のことを局所座標系、$(U_\la,\varphi_\la)$のことを座標近傍、その組$\{(U_\la,\varphi_\la)\}_{\la\in\La}$のことを座標近傍系という。
以下$\H^*$から$\G\backslash\H^*$への自然な写像を$\pi:z\mapsto\G z$とおき、$\G\backslash\H^*$の各点$\A=\pi(z_0)$に対しその座標近傍$(U_\A,\varphi_\A)\;(\A\in U_\A)$を次のように定める。
方針
前回の記事
の補題3から$z_0\in\H^*$の近傍$U$であって
$\g U\cap U\neq\emptyset\iff\g\in\G_{z_0}$
を満たすようなものが存在する。必要に応じて$\bigcap_{\g\in\G_{z_0}}\g U$を再び$U$と置くことで$U$は$\G_{z_0}$の作用に対して不変であるものとしてよい。
このとき$\pi|_U:U\to\pi(U)$の逆像は$\pi^{-1}(\G z)=\G_{z_0}z$によって与えられる。実際$\G z=\G w$が成り立つとき、ある$\g\in\G$によって$\g z=w$と表せるので$w\in\g U\cap U$となり、$U$の取り方から$\g\in\G_{z_0}$つまり$w\in \G_{z_0}z$がわかる。また$\pi$は連続な開写像であったのでこれによって位相同型$\pi(U)\simeq\G_{z_0}\backslash U$が得られる。
したがって正則写像$f:U\to\C$を$\G_{z_0}$の作用に対して不変で、$f\circ\pi|_U^{-1}:\pi(U)\to\C$が単射であるように取れれば、これは座標近傍$(\pi(U),f\circ\pi|_U^{-1})$を成すことになる。
通常点における座標近傍
$\A$が通常点のとき、$\G_{z_0}=Z(\G)$より恒等写像$f:z\mapsto z$は上のような性質を満たすので、座標近傍$(\pi(U),\pi|_U^{-1})$が得られる。
楕円点における座標近傍
$\A$が楕円点のとき、$\;e=|\G_{z_0}/Z(\G)|$とし、$\s z_0=i$なる$\s\in SL_2(\R)$を取ると$\G_{z_0}\cdot\{\pm I\}$は
$$\g=\s^{-1}k(\pi/e)\s\quad(k(\t)=\M{\cos\t}{-\sin\t}{\sin\t}{\cos\t})$$
によって生成される。また$k(\t)$の固有値は$e^{\pm i\t}$なので
$$\M{-\ol{z_0}}{z_0}{-1}{1}^{-1}\g\M{-\ol{z_0}}{z_0}{-1}1=\M\z00{\z^{-1}}\quad(\z=e^{\pm\pi i/e})$$
と対角化できる。特に
$$\M1{-z_0}1{-\ol{z_0}}\g=\M\z00{\z^{-1}}\M1{-z_0}1{-\ol{z_0}}$$
つまり
$$\frac{\g z-z_0}{\g z-\ol{z_0}}=e^{\pm 2\pi i/e}\frac{z-z_0}{z-\ol{z_0}}$$
が成り立つので
$$f:z\mapsto\l(\frac{z-z_0}{z-\ol{z_0}}\r)^e$$
は$\G_{z_0}$の作用に対し不変であり、座標近傍$(\pi(U),f\circ\pi|_U^{-1})$が得られる(単射性については省略)。
尖点における座標近傍
$\A$が楕円点のとき、$\s z_0=\infty$なる$\s\in SL_2(\R)$を取るとある$h>0$によって
$$\s\G_{z_0}\s^{-1}\cdot\{\pm I\}=\l\{\pm\M1{nh}01\mid n\in\Z\r\}$$
が成り立っていたので
$$f(z)=\l\{\begin{array}{cl}e^{2\pi i\s z/h}&(z\neq z_0)\\0&(z=z_0)\end{array}\r.$$
は$\G_{z_0}$の作用に対し不変であり、座標近傍$(\pi(U),f\circ\pi|_U^{-1})$が得られる。
補足
通常点近傍と基本領域との対応
前々回の記事
で紹介した領域
$\O=\{z\in\H\mid d(z,z_0)< d(z,\g z_0)\;,\forall\g\in\G\setminus Z(\G)\}$
は$z_0$が通常点であることから$z_0\in\O$であり、また基本領域であることから
$\g\O\cap\O\neq\emptyset\iff\g\in Z(\G)$
を満たす。
したがって✔方針のような$U$としてこの$\O$が取れ、通常点近傍に定まる局所座標系は$\G\backslash\H^*$と適当な基本領域を対応付ける写像に他ならないことがわかる(これによって$\O$の境界を除くすべての通常点を包む座標近傍が定まる)。
楕円点近傍のイメージ
$\rho=\M 1{-z_0}1{-\ol{z_0}}$
に対して
$W_r=\{z\in\C\mid|z|< r\},\quad U_r=\rho^{-1}W_r=\{z\in\H\mid|\rho z|< r\}$
とおくと、上での議論から$\G_{z_0}$の生成元$\g$に対して
$\rho(\g z)=\z^2\rho z$
特に
$|\rho(\g z)|=|\rho z|$
が成り立っていたので$U_r$は$\G_{z_0}$の作用に対して不変となる。また一次変換の円円対応に注意すると、$r$を十分小さく取れば✔方針のような$U$として$U_r$が取れることがわかる。
したがって楕円点近傍の局所座標は
$\pi(U_r)\to\G_{z_0}\backslash U_r\to\rho\G_{z_0}\rho^{-1}\backslash W_r\to W_{r^e}$
という図式によって定まっていることがわかる。
この説明だけだと少しイメージしづらいので具体的に$\G=SL_2(\Z)$の楕円点$z_0=e^{2\pi i/3}$(位数$3$)の場合を考えてみよう。
画像がデカいので折りたたみ
$\G$の基本領域を以下のように取り、$z_0$の周りに円を書いてみる。
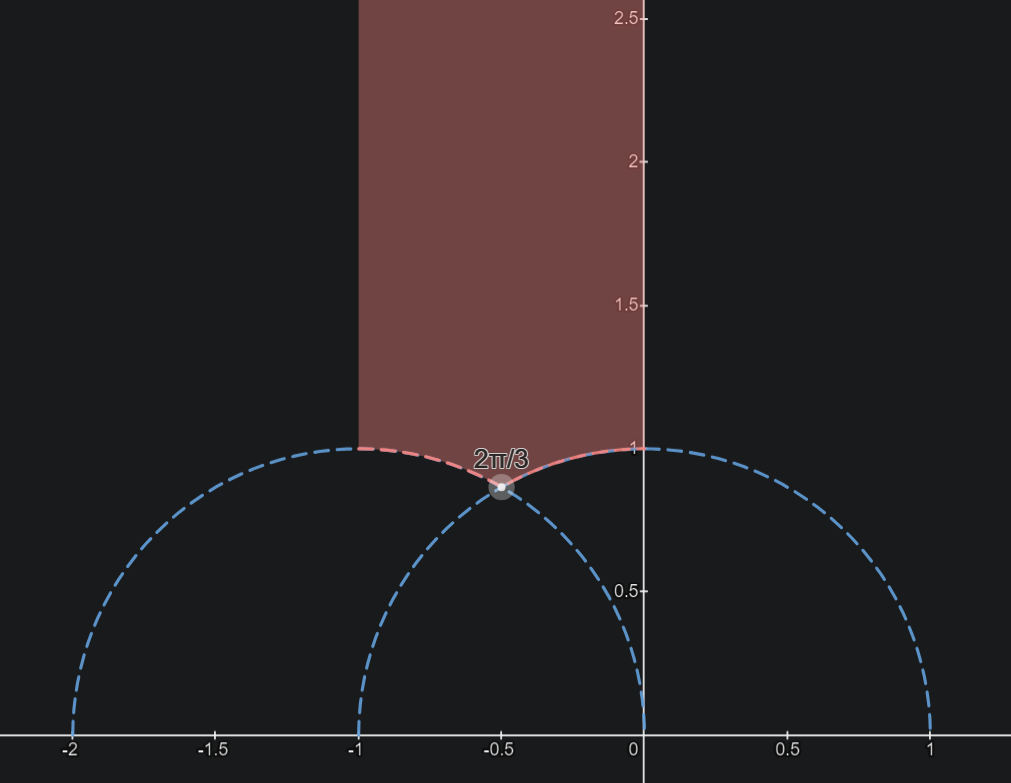 Γ\ℍのイメージ
Γ\ℍのイメージ
 Γ\Uのイメージ
Γ\Uのイメージ
この白い円の中身は$\rho$によって次のような領域に写される。
 ρΓρ^-1\Wのイメージ
ρΓρ^-1\Wのイメージ
そしてこれは$z\mapsto z^3$によって開円盤に写されることとなる。
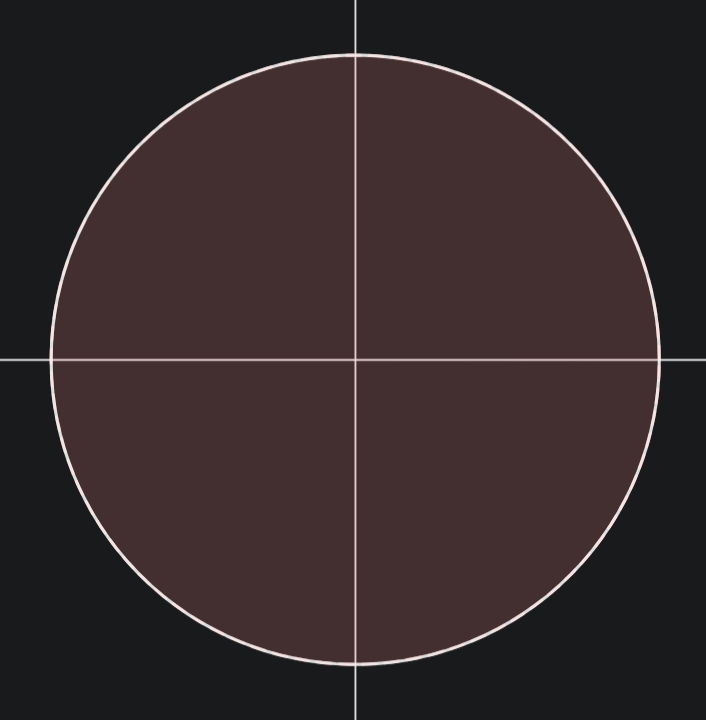 Wのイメージ
Wのイメージ
これが楕円点近傍における座標近傍の大まかなイメージとなる。
尖点近傍のイメージ
$\H^*$における尖点の近傍(基本近傍系)は$\infty$の近傍
$U_l^*=\{z\in\H\mid\Im(z)>l\}\cup\{\infty\}$
の$\s\;(\s z_0=\infty)$による引き戻し$U^*=\s^{-1}U_l^*$によって定めていたのであった。
また明らかに$\s\G_{z_0}\s^{-1}$の作用に対して$U_l^*$は不変なので$U^*$も$\G_{z_0}$の作用に対して不変となる。特に$l$を十分大きく取れば✔方針のような$U$として$U^*$が取れることがわかる。
したがって尖点近傍の局所座標は
$\pi(U^*)\to\G_{z_0}\backslash U^*\to\rho\G_{z_0}\rho^{-1}\backslash U_l^*\to W_r\quad(r=e^{-2\pi l/h})$
という図式によって定まっていることがわかる。
リーマン面全体としてのイメージ
結局のところ$\G\backslash\H^*$はどのような図形を定めるのか、ということについてはtsujimotterさんの
この記事
や
こちらの記事
で直感的・視覚的に説明されているのでよければ参照されたい。
