箱と玉の微分（４） シューア多項式の微分
はじめに
こんにちは、Kambing ゆっくんです。シリーズ「箱と玉の微分」の第四回です。
第一回
では、箱と玉に微分に似た数理構造があることを発見し、箱と玉の微分として定式化しました。
第二回
では、完全対称式、基本対称式の微分を紹介しました。
第三回
では、完全対称式と基本対称式の関係を考えました。
今回は、対称式の中でも中心的な役割を持つ シューア多項式 の微分について考えます。
完全対称式や基本対称式は、主に代数方程式の解法を巡る研究の中で、１９世紀までには知られていたようです。そして20世紀初頭にイサイ・シューア(Issai Schur)という数学者が、表現論の研究の中で新しい対称式を導入しました。それが今日シューア多項式（および歪みシューア多項式）と呼ばれている対称式です。シューア多項式は、対称式の中でも中心的な役割を果たし、対称群$\mathfrak{S}_n$の既約指標として組合せ論、幾何学、物理学の様々な文脈で現れる重要な存在です。シューア多項式は自然数の分割（またはヤング図形）を変数に持ちます。
自然数の分割
自然数の分割$\lambda=(\lambda_1,\lambda_2,\cdots)$とは$\lambda_i\in\mathbb{Z}_{\ge0},\; \lambda_1\ge\lambda_2\ge\cdots\ge0$を満たす整数列で、$|\lambda|=\lambda_1+\lambda_2+\cdots$を$\lambda$の大きさ、$\lambda$の非零要素の数$l(\lambda)$を$\lambda$の長さと呼びます。たとえば$\lambda=(5,3,1,1)$とすると、大きさは$|\lambda|=5+3+1+1=10$、長さは$l(\lambda)=4$となります。
ヤング図形
自然数の分割$\lambda$に対して、「第１行に$\lambda_1$個のマス」、「第２行に$\lambda_2$個のマス」、・・・というようにマスを並べて図形を作ることができます。これをヤング図形$\lambda$と言います。
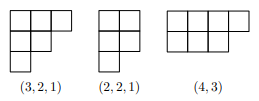ヤング図形の例
ヤング図形$\lambda$を、左上から右下への斜め４５度の対角線を軸にして180度回転させた形を転置と呼び、$\lambda'$と書きます。
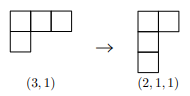転置の例
大きなヤング図形$\lambda$と小さなヤング図形$\mu$があるとき、$\lambda$から$\mu$の形のマスを取り除いた図形を歪みヤング図形と呼び、$\lambda/\mu$と書きます。
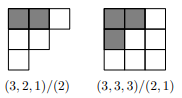歪みヤング図形の例
また歪みヤング図形が次に示す形となるときには、特別な名前を付けます。
分割$\lambda, \mu$について
- 各$i\in\{0,1,\cdots\}$で$0\le\lambda_i-\mu_i\le1$であるとき、$\lambda/\mu$を縦帯(vertical strip)と呼びます。
- 転置$\lambda',\mu'$について$\lambda'/\mu'$が縦帯であるとき、$\lambda/\mu$を横帯(horizontal strip)と呼びます。
つまり、横帯は下の図のように、白いマスが縦に二つ以上ない形となります。
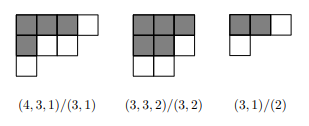横帯の例
さてこれでようやくシューア多項式（と歪みシューア多項式）を定義できます。
シューア多項式と歪みシューア多項式
シューア多項式と歪みシューア多項式は、基本対称式$\boldsymbol{e}_n$を用いて次の行列式で定義される対称式です。
$$
\begin{array}{ccc}
\boldsymbol{s}_\lambda \!\!\!&=&\!\!\! \det \bigl( \boldsymbol{e}_{\lambda_i'-i+j} \bigr)_{1\le \,i,\,j \,\le \,l'} \\[6pt]
\boldsymbol{s}_{\lambda/\mu} \!\!\!&=&\!\!\! \det \bigl( \boldsymbol{e}_{\lambda_i'-\mu_j'-i+j} \bigr)_{1\le \,i,\,j \,\le \,l'}
\end{array}
$$
ただし
- $i, j$はそれぞれ行、列方向のインデックス
- $l'=l(\lambda')$
- $n\lt0$ のとき $\boldsymbol{e}_n=0$
- $j \gt l(\mu')$のとき$\mu_j'=0$
とします。
実際に書き出してみましょう。$\lambda=(3,2,1)$とすると、シューア多項式$\boldsymbol{s}_{\!\lambda}$は
$$
\boldsymbol{s}_{(3,2,1)}=
\left|
\vphantom{\begin{matrix} a \\[28pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{e}_{3-1+1} & \boldsymbol{e}_{3-1+2} & \boldsymbol{e}_{3-1+3} \\
\boldsymbol{e}_{2-2+1} & \boldsymbol{e}_{2-2+2} & \boldsymbol{e}_{2-2+3} \\
\boldsymbol{e}_{1-3+1} & \boldsymbol{e}_{1-3+2} & \boldsymbol{e}_{1-3+3}
\end{matrix}
\right|
=
\left|
\vphantom{\begin{matrix} a \\[28pt] a \end{matrix}}
\begin{matrix}
\;\;\boldsymbol{e}_3 & \!\!\!\boldsymbol{e}_4 & \!\!\!\boldsymbol{e}_5\;\; \\[4pt]
\;\;\boldsymbol{e}_1 & \!\!\!\boldsymbol{e}_2 & \!\!\!\boldsymbol{e}_3\;\; \\[4pt]
\;\;0 & \!\!\!1 & \!\!\!\boldsymbol{e}_1\;\;
\end{matrix}
\right|
$$
となります。$\boldsymbol{e}$の大きさに注目すると、各行は左から右へ順に1ずつ大きくなること（列逓増性）が分かります。
また$\lambda=(3,2,1),\;\mu=(2)$とすると、これらの転置は$\lambda'=(3,2,1),\;\mu'=(1,1)$なので、歪みシューア多項式$\boldsymbol{s}_{\!\lambda/\mu}$は
$$
\boldsymbol{s}_{(3,2,1)/(2)}
=\left|
\vphantom{\begin{matrix} a \\[28pt] a \end{matrix}}
\begin{matrix}
\;\;\boldsymbol{e}_{3-1-1+1} & \!\!\!\boldsymbol{e}_{3-1-1+2} & \!\!\!\boldsymbol{e}_{3-0-1+3}\;\; \\[4pt]
\;\;\boldsymbol{e}_{2-1-2+1} & \!\!\!\boldsymbol{e}_{2-1-2+2} & \!\!\!\boldsymbol{e}_{2-0-2+3}\;\; \\[4pt]
\;\;\boldsymbol{e}_{1-1-3+1} & \!\!\!\boldsymbol{e}_{1-1-3+2} & \!\!\!\boldsymbol{e}_{1-0-3+3}\;\;
\end{matrix}
\right|
=\left|
\vphantom{\begin{matrix} a \\[28pt] a \end{matrix}}
\begin{matrix}
\;\;\boldsymbol{e}_{2} & \!\!\!\boldsymbol{e}_{3} & \!\!\!\boldsymbol{e}_{5}\;\; \\[4pt]
\;\;1 & \!\!\!\boldsymbol{e}_{1} & \!\!\!\boldsymbol{e}_{3}\;\; \\[4pt]
\;\;0 & \!\!\!0 & \!\!\!\boldsymbol{e}_{1}\;\;
\end{matrix}
\right|
$$
となります。
行列式の微分
行列式の微分を考えてみましょう。そもそも行列式の定義は、
$$
\det\boldsymbol{F}=\sum_{\sigma\in\mathfrak{S}_n}\mathrm{sgn}(\sigma)\boldsymbol{f}_{1\,\sigma(1)}\boldsymbol{f}_{2\,\sigma(2)}\cdots\boldsymbol{f}_{n\,\sigma(n)}
$$
でした。これは本質的に$n$項の積なので、行列式の微分は積の法則をｎ項に拡張した場合と同じと考えることができます。3×3の行列を例に考えれば、
一階微分の形
$$
\bigcirc_1\boldsymbol{F}=
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\bigcirc_1\boldsymbol{f}_{\!11} & \boldsymbol{f}_{\!12} & \boldsymbol{f}_{\!12} \\[13pt]
\bigcirc_1\boldsymbol{f}_{\!21} & \boldsymbol{f}_{\!22} & \boldsymbol{f}_{\!23} \\[13pt]
\bigcirc_1\boldsymbol{f}_{\!31} & \boldsymbol{f}_{\!32} & \boldsymbol{f}_{\!33} \\
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{f}_{\!11} & \bigcirc_1\boldsymbol{f}_{\!12} & \boldsymbol{f}_{\!13}\\[13pt]
\boldsymbol{f}_{\!21} & \bigcirc_1\boldsymbol{f}_{\!22} & \boldsymbol{f}_{\!23}\\[13pt]
\boldsymbol{f}_{\!31} & \bigcirc_1\boldsymbol{f}_{\!32} & \boldsymbol{f}_{\!33}\\
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{f}_{\!11} & \boldsymbol{f}_{\!12} & \bigcirc_1\boldsymbol{f}_{\!13}\\[13pt]
\boldsymbol{f}_{\!21} & \boldsymbol{f}_{\!22} & \bigcirc_1\boldsymbol{f}_{\!23}\\[13pt]
\boldsymbol{f}_{\!31} & \boldsymbol{f}_{\!32} & \bigcirc_1\boldsymbol{f}_{\!33}
\end{matrix}
\right|
$$
これは$\bigcirc_1$の三項の積の法則と同じ形をしています。
$$
\bigcirc_1 \left(\boldsymbol{ABC}\right)=\left(\bigcirc_1\boldsymbol{A}\right)\boldsymbol{BC}+\boldsymbol{A}\left(\bigcirc_1\boldsymbol{B}\right)\boldsymbol{C}+\boldsymbol{AB}\left(\bigcirc_1\boldsymbol{C}\right)
$$
二階微分の形
$$
\bigcirc_2\boldsymbol{F}=
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\bigcirc_2\boldsymbol{f}_{\!11} & \boldsymbol{f}_{\!12} & \boldsymbol{f}_{\!12} \\[13pt]
\bigcirc_2\boldsymbol{f}_{\!21} & \boldsymbol{f}_{\!22} & \boldsymbol{f}_{\!23} \\[13pt]
\bigcirc_2\boldsymbol{f}_{\!31} & \boldsymbol{f}_{\!32} & \boldsymbol{f}_{\!33} \\
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{f}_{\!11} & \bigcirc_2\boldsymbol{f}_{\!12} & \boldsymbol{f}_{\!13}\\[13pt]
\boldsymbol{f}_{\!21} & \bigcirc_2\boldsymbol{f}_{\!22} & \boldsymbol{f}_{\!23}\\[13pt]
\boldsymbol{f}_{\!31} & \bigcirc_2\boldsymbol{f}_{\!32} & \boldsymbol{f}_{\!33}\\
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{f}_{\!11} & \boldsymbol{f}_{\!12} & \bigcirc_2\boldsymbol{f}_{\!13}\\[13pt]
\boldsymbol{f}_{\!21} & \boldsymbol{f}_{\!22} & \bigcirc_2\boldsymbol{f}_{\!23}\\[13pt]
\boldsymbol{f}_{\!31} & \boldsymbol{f}_{\!32} & \bigcirc_2\boldsymbol{f}_{\!33}
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\bigcirc_1\boldsymbol{f}_{\!11} & \!\!\!\!\!\bigcirc_1\boldsymbol{f}_{\!12} & \!\!\!\boldsymbol{f}_{\!13}\\[13pt]
\bigcirc_1\boldsymbol{f}_{\!21} & \!\!\!\!\!\bigcirc_1\boldsymbol{f}_{\!22} & \!\!\!\boldsymbol{f}_{\!23}\\[13pt]
\bigcirc_1\boldsymbol{f}_{\!31} & \!\!\!\!\!\bigcirc_1\boldsymbol{f}_{\!32} & \!\!\!\boldsymbol{f}_{\!33}
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{f}_{\!11} & \!\!\!\!\bigcirc_1\boldsymbol{f}_{\!12} & \!\!\!\!\bigcirc_1\boldsymbol{f}_{\!13}\\[13pt]
\boldsymbol{f}_{\!21} & \!\!\!\!\bigcirc_1\boldsymbol{f}_{\!22} & \!\!\!\!\bigcirc_1\boldsymbol{f}_{\!23}\\[13pt]
\boldsymbol{f}_{\!31} & \!\!\!\!\bigcirc_1\boldsymbol{f}_{\!32} & \!\!\!\!\bigcirc_1\boldsymbol{f}_{\!33}
\end{matrix}
\right|
+
\left|
\vphantom{\begin{matrix} a \\[52pt] a \end{matrix}}
\begin{matrix}
\bigcirc_1\boldsymbol{f}_{\!11} & \!\!\!\boldsymbol{f}_{\!12} & \!\!\!\!\!\bigcirc_1\boldsymbol{f}_{\!13}\\[13pt]
\bigcirc_1\boldsymbol{f}_{\!21} & \!\!\!\boldsymbol{f}_{\!22} & \!\!\!\!\!\bigcirc_1\boldsymbol{f}_{\!23}\\[13pt]
\bigcirc_1\boldsymbol{f}_{\!31} & \!\!\!\boldsymbol{f}_{\!32} & \!\!\!\!\!\bigcirc_1\boldsymbol{f}_{\!33}
\end{matrix}
\right|
$$
これは$\bigcirc_2$の三項の積の法則と同じ形をしています。
$$
\bigcirc_2 \left(\boldsymbol{ABC}\right)=\left(\bigcirc_2\boldsymbol{A}\right)\boldsymbol{BC}+\boldsymbol{A}\left(\bigcirc_2\boldsymbol{B}\right)\boldsymbol{C}+\boldsymbol{AB}\left(\bigcirc_2\boldsymbol{C}\right)+\left(\bigcirc_1\boldsymbol{A}\right)\left(\bigcirc_1\boldsymbol{B}\right)\boldsymbol{C}+\boldsymbol{A}\left(\bigcirc_1\boldsymbol{B}\right)\left(\bigcirc_1\boldsymbol{C}\right)+\left(\bigcirc_1\boldsymbol{A}\right)\boldsymbol{B}\left(\bigcirc_1\boldsymbol{C}\right)
$$
以上の例から、高階の微分や n×n の行列式も直感的に理解できると思います。
シューア多項式の微分
先ほど書き出した$\boldsymbol{s}_{(3,2,1)}$のヤコビ・トゥルーディの行列式に$\bigcirc_2$を入れて、行列式の微分公式で展開してみましょう。
$$
\begin{align}
\bigcirc_2\boldsymbol{s}_{(3,2,1)}
&=
\bigcirc_2\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\;\;\boldsymbol{e}_3 & \boldsymbol{e}_4 & \boldsymbol{e}_5\;\;\; \\[11pt]
\;\;\;\boldsymbol{e}_1 & \boldsymbol{e}_2 & \boldsymbol{e}_3\;\;\; \\[11pt]
\;\;\;0 & 1 & \boldsymbol{e}_1\;\;\;
\end{matrix}
\right| \\[10pt]
&=\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\:\bigcirc_2\boldsymbol{e}_3 & \!\boldsymbol{e}_4 & \!\boldsymbol{e}_5\;\; \\[11pt]
\:\bigcirc_2\boldsymbol{e}_1 & \!\boldsymbol{e}_2 & \!\boldsymbol{e}_3\;\; \\[11pt]
\:\bigcirc_2\:0 & \!1 & \!\boldsymbol{e}_1\;\;
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\boldsymbol{e}_3 & \!\!\bigcirc_2\boldsymbol{e}_4 & \!\boldsymbol{e}_5\; \\[11pt]
\;\boldsymbol{e}_1 & \!\!\bigcirc_2\boldsymbol{e}_2 & \!\boldsymbol{e}_3\; \\[11pt]
\;0 & \!\!\bigcirc_2\:1 & \!\boldsymbol{e}_1\;\;
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\boldsymbol{e}_3 & \!\boldsymbol{e}_4 & \bigcirc_2\boldsymbol{e}_5\; \\[11pt]
\;\boldsymbol{e}_1 & \!\boldsymbol{e}_2 & \bigcirc_2\boldsymbol{e}_3\; \\[11pt]
\;0 & \!1 & \bigcirc_2\boldsymbol{e}_1
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\bigcirc_1\boldsymbol{e}_3 & \!\!\!\bigcirc_1\boldsymbol{e}_4 & \!\!\!\boldsymbol{e}_5 \\[11pt]
\bigcirc_1\boldsymbol{e}_1 & \!\!\!\bigcirc_1\boldsymbol{e}_2 & \!\!\!\boldsymbol{e}_3 \\[11pt]
\bigcirc_1\,0 & \!\!\!\bigcirc_1\,1 & \!\!\!\boldsymbol{e}_1
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\boldsymbol{e}_3 & \!\!\!\bigcirc_1\boldsymbol{e}_4 & \!\!\!\bigcirc_1\boldsymbol{e}_5 \\[11pt]
\boldsymbol{e}_1 & \!\!\!\bigcirc_1\boldsymbol{e}_2 & \!\!\!\bigcirc_1\boldsymbol{e}_3 \\[11pt]
0 & \!\!\!\bigcirc_1\,1 & \!\!\!\bigcirc_1\boldsymbol{e}_1
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\bigcirc_1\boldsymbol{e}_3 & \!\!\!\boldsymbol{e}_4 & \!\!\!\bigcirc_1\boldsymbol{e}_5 \\[11pt]
\bigcirc_1\boldsymbol{e}_1 & \!\!\!\boldsymbol{e}_2 & \!\!\!\bigcirc_1\boldsymbol{e}_3 \\[11pt]
\bigcirc_1\,0 & \!\!\!1 & \!\!\!\bigcirc_1\boldsymbol{e}_1
\end{matrix}
\right|
\end{align}
$$
ヤコビ・トゥルーディの行列式は、要素が$\boldsymbol{e}$のみから成ること、列逓増性を持つことから、次の面白い特徴を持っています。
フェルミオン的性質
同じ色の玉が二つ以上入ることはできません。これは要素$\boldsymbol{e}$の性質を、行列式が引き継いだものです。つまり、
$$
\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\:\bigcirc_2\boldsymbol{e}_3 & \!\boldsymbol{e}_4 & \!\boldsymbol{e}_5\;\; \\[11pt]
\:\bigcirc_2\boldsymbol{e}_1 & \!\boldsymbol{e}_2 & \!\boldsymbol{e}_3\;\; \\[11pt]
\:\bigcirc_2\:0 & \!1 & \!\boldsymbol{e}_1\;\;
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\boldsymbol{e}_3 & \!\!\bigcirc_2\boldsymbol{e}_4 & \!\boldsymbol{e}_5\; \\[11pt]
\;\boldsymbol{e}_1 & \!\!\bigcirc_2\boldsymbol{e}_2 & \!\boldsymbol{e}_3\; \\[11pt]
\;0 & \!\!\bigcirc_2\:1 & \!\boldsymbol{e}_1\;\;
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\boldsymbol{e}_3 & \!\boldsymbol{e}_4 & \bigcirc_2\boldsymbol{e}_5\; \\[11pt]
\;\boldsymbol{e}_1 & \!\boldsymbol{e}_2 & \bigcirc_2\boldsymbol{e}_3\; \\[11pt]
\;0 & \!1 & \bigcirc_2\boldsymbol{e}_1
\end{matrix}
\right|
\quad=\quad
\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\;\;0 & \boldsymbol{e}_4 & \boldsymbol{e}_5\;\;\; \\[11pt]
\;\;\;0 & \boldsymbol{e}_2 & \boldsymbol{e}_3\;\;\; \\[11pt]
\;\;\;0 & 1 & \boldsymbol{e}_1\;\;\;
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\;\;\boldsymbol{e}_3 & 0 & \boldsymbol{e}_5\;\;\; \\[11pt]
\;\;\;\boldsymbol{e}_1 & 0 & \boldsymbol{e}_3\;\;\; \\[11pt]
\;\;\;0 & 0 & \boldsymbol{e}_1\;\;\;
\end{matrix}
\right|
+\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\;\;\boldsymbol{e}_3 & \boldsymbol{e}_4 & 0\;\;\; \\[11pt]
\;\;\;\boldsymbol{e}_1 & \boldsymbol{e}_2 & 0\;\;\; \\[11pt]
\;\;\;0 & 1 & 0\;\;\;
\end{matrix}
\right|
\quad=\quad0
$$
となります。
絶対零度的性質
玉は左端の列（第１列）から右方向へ隙間なく埋まっていきます。これは$\boldsymbol{e}$が右方向へ1ずつ大きくなること（列逓増性）から生まれる性質です。
もう少し詳しく見てみましょう。行列式には、同じ列があるとき 0 になるという性質があります。$\bigcirc_1$の微分により列の各$\boldsymbol{e}$の大きさが1だけ小さくなったとき、左隣の列の各$\boldsymbol{e}$の大きさと一致して、行列式が 0 になることがあります。今回の場合は、次の２つの行列式で 列の一致 が起こります。
$$ \left| \vphantom{\begin{matrix} a \\[48pt] a \end{matrix}} \begin{matrix} \boldsymbol{e}_3 & \!\!\!\bigcirc_1\boldsymbol{e}_4 & \!\!\!\bigcirc_1\boldsymbol{e}_5 \\[11pt] \boldsymbol{e}_1 & \!\!\!\bigcirc_1\boldsymbol{e}_2 & \!\!\!\bigcirc_1\boldsymbol{e}_3 \\[11pt] 0 & \!\!\!\bigcirc_1\,1 & \!\!\!\bigcirc_1\boldsymbol{e}_1 \end{matrix} \right| \;\:=\;\: \left| \vphantom{\begin{matrix} a \\[48pt] a \end{matrix}} \begin{matrix} \;\;\;\boldsymbol{e}_3 & \boldsymbol{e}_3 & \boldsymbol{e}_4\;\;\; \\[11pt] \;\;\;\boldsymbol{e}_1 & \boldsymbol{e}_1 & \boldsymbol{e}_2\;\;\; \\[11pt] \;\;\;0 & 0 & 1\;\;\; \end{matrix} \right| \;\:=\;\:0 \quad\quad\quad \leftarrow\:\text{第１列と第２列が同じ} $$
$$ \left| \vphantom{\begin{matrix} a \\[48pt] a \end{matrix}} \begin{matrix} \bigcirc_1\boldsymbol{e}_3 & \!\!\!\boldsymbol{e}_4 & \!\!\!\bigcirc_1\boldsymbol{e}_5 \\[11pt] \bigcirc_1\boldsymbol{e}_1 & \!\!\!\boldsymbol{e}_2 & \!\!\!\bigcirc_1\boldsymbol{e}_3 \\[11pt] \bigcirc_1\,0 & \!\!\!1 & \!\!\!\bigcirc_1\boldsymbol{e}_1 \end{matrix} \right| \;\:=\;\: \left| \vphantom{\begin{matrix} a \\[48pt] a \end{matrix}} \begin{matrix} \;\;\;\boldsymbol{e}_2 & \boldsymbol{e}_4 & \boldsymbol{e}_4\;\;\; \\[11pt] \;\;\;1 & \boldsymbol{e}_2 & \boldsymbol{e}_2\;\;\; \\[11pt] \;\;\;0 & 1 & 1\;\;\; \end{matrix} \right| \;\:=\;\:0\quad\quad\quad \leftarrow\:\text{第２列と第３列が同じ} $$
つまり「玉が入っている列」の「左隣の列」が空だと、列の一致が起こることが分かります。
これら二つの性質から、第１列から第２列まで$\bigcirc_1$が隙間なく玉が入る項だけが残り、
$$
\bigcirc_2\boldsymbol{s}_{(3,2,1)}
=\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\bigcirc_1\boldsymbol{e}_3 & \!\!\!\bigcirc_1\boldsymbol{e}_4 & \!\!\!\boldsymbol{e}_5 \\[11pt]
\bigcirc_1\boldsymbol{e}_1 & \!\!\!\bigcirc_1\boldsymbol{e}_2 & \!\!\!\boldsymbol{e}_3 \\[11pt]
\bigcirc_1\,0 & \!\!\!\bigcirc_1\,1 & \!\!\!\boldsymbol{e}_1
\end{matrix}
\right|
\;\:=\;\:
\left|
\vphantom{\begin{matrix} a \\[48pt] a \end{matrix}}
\begin{matrix}
\;\;\;\boldsymbol{e}_2 & \boldsymbol{e}_3 & \boldsymbol{e}_5\;\;\; \\[11pt]
\;\;\;1 & \boldsymbol{e}_1 & \boldsymbol{e}_3\;\;\; \\[11pt]
\;\;\;0 & 0 & \boldsymbol{e}_1\;\;\;
\end{matrix}
\right|
$$
となります。ところでこれは上で計算した歪みシューア多項式$\boldsymbol{s}_{(3,2,1)/(2)}$のヤコビ・トゥルーディの行列式と一致します。他の場合でも同じで、結局、
$$
\bigcirc_n\boldsymbol{s}_\lambda=\boldsymbol{s}_{\lambda/(n)}
$$
と分かります。さらに
リトルウッド・リチャードソンの規則
と呼ばれる関係式から、
$$
\boldsymbol{s}_{\lambda/(n)}=\sum_\mu \boldsymbol{s}_{\!\mu}
$$
（ここで$|\mu|=|\lambda|-n$かつ$\lambda/\mu$は横帯）なので、シューア多項式の微分は次の形となります。
$$
\bigcirc_n \,\boldsymbol{s}_{\!\lambda} = \sum_\mu \boldsymbol{s}_{\!\mu} \tag{微1}
$$
ここで$\mu$は大きさ$|\lambda|-n$の分割で、$\lambda/\mu$が横帯(horizontal strip)となるように動きます。
検算しましょう
$\boldsymbol{s}_{(2,1)}$の場合について計算してみましょう。ただし簡単のため、
$$
\boldsymbol{s}_{(2)}=\frac{1}{2}\boldsymbol{p}_2+\frac{1}{2}\boldsymbol{p}_1^2, \quad \boldsymbol{s}_{(1,1)}=-\frac{1}{2}\boldsymbol{p}_2+\frac{1}{2}\boldsymbol{p}_1^2
$$
は分かっているものとします。$\boldsymbol{s}_{(2,1)}$は大きさ3の箱なので、
$$
\boldsymbol{s}_{(2,1)}=a\,\boldsymbol{p}_3+b\,\boldsymbol{p}_2\boldsymbol{p}_1+c\,\boldsymbol{p}_1^3 \tag{検1}
$$
と置きます。(微1)より
$$
\begin{align}
\bigcirc_1 \boldsymbol{s}_{(2,1)}&=\boldsymbol{s}_{(2)}+\boldsymbol{s}_{(1,1)}=\boldsymbol{p}_1^2\\[10pt]
\bigcirc_3 \boldsymbol{s}_{(2,1)}&=0
\end{align}
$$
となります。また(検1)より、
$$
\begin{align}
\bigcirc_1 \left( a\,\boldsymbol{p}_3+b\,\boldsymbol{p}_2\boldsymbol{p}_1+c\,\boldsymbol{p}_1^3 \right)
&= b\,\boldsymbol{p}_2 + 3c\,\boldsymbol{p}_1^2 \\[10pt]
\bigcirc_3 \left( a\,\boldsymbol{p}_3+b\,\boldsymbol{p}_2\boldsymbol{p}_1+c\,\boldsymbol{p}_1^3 \right)
&= a+b+c
\end{align}
$$
となるので、次の連立方程式が成り立ちます。
$$
\begin{align}
b &= 0\\
3c &= 1\\
a+b+c &= 0
\end{align}
$$
これを解いて(検1)に代入することにより
$$
\boldsymbol{s}_{(2,1)}=-\frac{1}{3}\boldsymbol{p}_3+\frac{1}{3}\boldsymbol{p}_1^3
$$
が求まります。これは実際にヤコビ・トゥルーディの行列式から求める場合と一致しますので、気になる方は確かめてみてください。
コストカ数
コストカ数 という組合せ論に出てくる数は、箱と玉の微分を使うと、次のように簡潔に書けます。
$$
K_{\lambda\mu}=\bigcirc_{\!\mu} \boldsymbol{s}_{\!\lambda}
$$
ここで$\bigcirc_{\!\mu}\!=\!\bigcirc_{\!\mu_1}\!\!\bigcirc_{\!\mu_2}\!\cdots$とします。
つまりシューア多項式を一種の図形と考えると、コストカ数は、ある種の傾きのようなものと考えられます。
この記事を高評価した人
この記事に送られたバッジ
投稿者
