応用数学解説

文献あり

鏡映：ベクトルから八元数まで

四元数,鏡映,クリフォード代数

262

鏡映は、幾何学の基本的かつ重要な概念です。本記事は、この鏡映を様々な数学的構造の中で考察します。

ベクトル（任意次元）
複素数（2次元）
四元数（3次元および4次元）
八元数（7次元および8次元）
クリフォード代数（任意次元）

各代数に対して、鏡映の数学的表現を導出します。特に注目すべきは、次元が上がるにつれて背後の代数的構造が変化する点です。

鏡映

鏡映は、ある対象をある平面（鏡面）に関して反転させる幾何学的操作です。日常生活では鏡に映る像として経験されますが、数学的には非常に重要で基本的な変換の一つです。

$n$次元ユークリッド空間$V$において、ベクトル$\mathbf{v}$を単位法線ベクトル$\mathbf{n}\ (\|\mathbf{n}\| = 1)$で定義される超平面に関して鏡映したベクトル$\mathbf{v}'$は以下の式で与えられます：

法線による鏡映

$$ \mathbf{v}' = \mathbf{v} - 2(\mathbf{v} \cdot \mathbf{n})\mathbf{n} = (I - 2\mathbf{n}\mathbf{n}^{\mathsf T})\mathbf{v} $$

ここで$\cdot$はベクトルの内積で、$(\mathbf{v} \cdot \mathbf{n})\mathbf{n}$は$\mathbf v$の$\mathbf n$上への射影を表します。法線$\mathbf n$は鏡映面方向とは逆向きのベクトルです。$\mathbf v$から射影の逆向きに動かした$\mathbf{v} - (\mathbf{v} \cdot \mathbf{n})\mathbf{n}$は鏡映面との交点で、そこから更に同じだけ動かすことで鏡像を得ます。

右辺は、ベクトル$\mathbf{v}$に対する作用としての表現です。$\mathbf{n}\mathbf{n}^{\mathsf T}$は射影行列です。

中辺から右辺

$$ \begin{aligned} \mathbf{v} - 2(\mathbf{v} \cdot \mathbf{n})\mathbf{n} &=\mathbf{v} - 2\mathbf{n}(\mathbf{n} \cdot \mathbf{v}) \\ &=\mathbf{v} - 2\mathbf{n}(\mathbf{n}^{\mathsf T}\mathbf{v}) \\ &=(I - 2\mathbf{n}\mathbf{n}^{\mathsf T})\mathbf{v} \end{aligned} $$

鏡映面は、$n$次元では$n-1$次元の超平面となります。具体的には、2次元では1次元直線、3次元では2次元平面、4次元では3次元立体となります。

鏡映面

集合$\{\mathbf{v} - (\mathbf{v} \cdot \mathbf{n})\mathbf{n} \mid \mathbf{v} \in V \}$により構成される$n-1$次元の超平面が鏡映面となります。なお、3次元においては、ベクトル三重積の公式により$(\mathbf n × \mathbf v) × \mathbf n = \mathbf v - (\mathbf v \cdot \mathbf n)\mathbf n$となります。

鏡映の主な特徴：

等長変換：距離と角度を保存する。
向きを変える：左手系を右手系に、またはその逆に変換する。
二回適用すると元に戻る：$M^2 = I$（$M$は鏡映、$I$は恒等変換）

内積

鏡映の導出に必要となる内積について説明します。

ベクトル$\mathbf{a} = (a_1, a_2, \dots, a_n)$と$\mathbf{b} = (b_1, b_2, \dots, b_n)$の内積は以下のように定義されます。

ベクトルの内積

$$ \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + \dots + a_nb_n $$

内積の主な性質：

対称性：$\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$
線形性：$(\mathbf{a} + \mathbf{b}) \cdot \mathbf{c} = \mathbf{a} \cdot \mathbf{c} + \mathbf{b} \cdot \mathbf{c}$
スカラー倍：$(k\,\mathbf{a}) \cdot \mathbf{b} = k(\mathbf{a} \cdot \mathbf{b})$
ノルムとの関係：$\mathbf{a} \cdot \mathbf{a} = \|\mathbf{a}\|^2$

内積は、ベクトル間の角度$\theta$を計算する際にも使用されます：

内積と角度の関係

$$ \mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\| \|\mathbf{b}\| \cos \theta \iff \cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|} $$

射影

ベクトルの内積を視覚的に表すと、2本のベクトルの向きを揃えて長さを掛けた値となります。向きを揃えるには垂線を引いて交点を求めます。これを射影と呼びます。どちらのベクトルを射影しても結果は同じです。7shi-ip

!FORMULA[33][36647][0]を!FORMULA[34][36678][0]に射影 $A$を$B$に射影
$\mathrm A \cdot \mathrm B = \mathrm A' \cdot \mathrm B = 2 \cdot 3 = 6$
$\mathrm A \cdot \mathrm B = \|\mathrm A\| \|\mathrm B\| \cos\theta$

特別な場合として、単位ベクトルとの内積が頻出で、鏡映でも使用されます。

ベクトル$\mathbf{v}$と単位ベクトル$\mathbf{n}$の内積は、射影されたベクトル$\mathbf{v_p}$の長さになります：$\mathbf{v} \cdot \mathbf{n}=\|\mathbf{v_p}\|$
内積に更に$\mathbf{n}$を掛ければ、射影されたベクトル$\mathbf{v_p}$が得られます：$(\mathbf{v} \cdot \mathbf{n})\mathbf{n}=\|\mathbf{v_p}\|\mathbf{n}=\mathbf{v_p}$
射影の作用を取り出せば射影行列（射影作用素）が得られますproj：$(\cdot \mathbf{n})\mathbf{n}=\mathbf{n}(\mathbf{n}\cdot)=\mathbf{n}\mathbf{n}^{\mathsf T}$

冪等行列

$\mathbf{n}^{\mathsf T}\mathbf{n}=I$より、射影行列は冪等行列です：$(\mathbf{n}\mathbf{n}^{\mathsf T})^2=\mathbf{n}\mathbf{n}^{\mathsf T}\mathbf{n}\mathbf{n}^{\mathsf T}=\mathbf{n}\mathbf{n}^{\mathsf T}$

代数系と幾何学の関係

鏡映は、様々な代数系の中で表現することができます。これらの代数系と幾何学の関係を理解することは、高次元空間や複雑な幾何学的操作を扱う上で非常に重要です。

主な代数系と対応する幾何学的空間：

実数ベクトル空間$\mathbb{R}^n$：n次元ユークリッド空間
複素数$\mathbb{C}$（可換、結合的）：2次元ユークリッド空間
四元数$\mathbb{H}$（非可換、結合的）：3次元ユークリッド空間、4次元ユークリッド空間
八元数$\mathbb{O}$（非可換、非結合的）：7次元ユークリッド空間、8次元ユークリッド空間
クリフォード代数$\mathrm{Cl}_{n,0}(\mathbb{R})$（非可換、結合的）：n次元ユークリッド空間

これらの代数系を用いることで、鏡映をより一般的かつ抽象的に表現することができます。特にクリフォード代数は、次元に依存せずに鏡映を表現できるため、高次元空間や複雑な幾何学的構造での操作の理解を深めるのに役立ちます。

次章からは、各代数系における鏡映の具体的な表現と性質について詳しく見ていきます。クリフォード代数については、他の代数系を扱った後に、それらを統合する形で導入し、その統一的な性質を強調します。

複素数

複素数$z = a + bi\ (a, b \in \mathbb{R})$に対して：

基底の2乗：$i^2=-1$
共役：$z^* = a - bi$
絶対値：$|z| = \sqrt{zz^*} = \sqrt{a^2 + b^2}$
実部：$\mathrm{Re}(z) = (z+z^*)/2 = a$
虚部：$\mathrm{Im}(z) = -i(z-z^*)/2 = b$（基底を含まない）
複素数の積：$(a + bi)(c + di) = (ac - bd) + (ad + bc)i$

複素数$z_1,z_2,z_3$について、以下の性質が成り立ちます。

可換性：$z_1z_2=z_2z_1$
結合性：$(z_1z_2)z_3=z_1(z_2z_3)$

複素数の実軸を$x$軸、虚軸を$y$軸と同一視します。

2次元ベクトルと複素数の同一視（複素数平面）

$$ (a,b) \cong a + bi $$

内積

複素数の内積は、共役との積の実部から得られます：

複素数の内積

$$ a \cdot b = \mathrm{Re}(a^*b) = \frac12(a^*b+b^*a) $$

$$ \begin{aligned} a^*b &=(a_0-a_1i)(b_0+b_1i) \\ &=(a_0b_0+a_1b_1)+(a_0b_1-a_1b_0)i \\ \end{aligned} $$
$\therefore \mathrm{Re}(a^*b)=a_0b_0+a_1b_1$

鏡映

2次元空間において、複素数$z$を単位複素数$n\ (|n| = 1)$で定義される直線に関して鏡映で移した複素数$z'$は以下の式で与えられます：

複素数による鏡映

$$ z'=-z^*n^2 $$

$$ \begin{aligned} z' &= z - 2(z \cdot n)n \\ &= z - (z^*n + n^*z)n \\ &= z - z^*n^2 - |n|^2z \\ &= -z^*n^2 \end{aligned} $$

四元数

四元数$q = a + bi + cj + dk\ (a,b,c,d \in \mathbb{R})$に対して：

基底の2乗：$i^2 = j^2 = k^2 = ijk = -1$
基底の積：$ij=k,\ jk=i,\ ki=j$
反交換性：$ij=-ji,\ jk=-kj,\ ki=-ik$
共役：$q^* = a - bi - cj - dk$
ノルム：$|q| = \sqrt{qq^*} = \sqrt{a^2 + b^2 + c^2 + d^2}$
逆元：$q^{-1} = q^* / |q|^2\ (q \neq 0)$
実部：$\mathrm{Re}(q) = (q+q^*)/2 = a$
虚部：$\mathrm{Im}(q) = (q-q^*)/2 = bi + cj + dk$（基底を含む）

四元数$q_1,q_2,q_3$について、以下の性質が成り立ちます。

非可換性：一般に$q_1q_2 \neq q_2q_1$（特定の条件下で可換）
結合性：$(q_1q_2)q_3=q_1(q_2q_3)$

四元数（3次元）

四元数は3次元と4次元が扱えますが、使い勝手がかなり異なります。まず扱いが簡単な3次元について見ていきます。

3次元ベクトルと純虚四元数の同一視

$$ (x, y, z) \cong xi + yj + zk $$

内積

純虚四元数の内積は、積の実部の符号反転から得られます：

純虚四元数の内積（3次元）

$$ v \cdot w = -\mathrm{Re}(vw) = -\frac12(vw+wv) $$

$$ \begin{aligned} vw &=(v_xi+v_yj+v_zk)(w_xi+w_yj+w_zk) \\ &=-(v_xw_x+v_yw_y+v_zw_z) \\ &\quad+(v_yw_z-v_zw_y)i+(v_zw_x-v_xw_z)j+(v_yw_z-v_zw_y)k \end{aligned} $$
$$ \therefore -\mathrm{Re}(vw)=v_xw_x+v_yw_y+v_zw_z = v \cdot w $$

外積

$vw$の虚部は外積です。外積の反交換性により、$\mathrm{Im}(vw)=-\mathrm{Im}(wv)$となり、反交換子$vw+wv$によって実部だけが残ります。

複素数との比較

四元数の反交換性により、複素数のような共役が不要となります。

鏡映

3次元空間において、純虚四元数$v$を単位純虚四元数$n\ (n^2 = -1)$で定義される平面に関して鏡映で移した純虚四元数$v'$は以下の式で与えられます：

純虚四元数による鏡映（3次元）

$$ v'=-nv^*n=nvn $$

$$ \begin{aligned} v' &= v - 2(v \cdot n)n \\ &= v + (vn + nv)n \\ &= v + vn^2 + nvn \\ &= nvn \end{aligned} $$

$v$が純虚四元数であることから、$v^* = -v$より$-nv^*n$とも表現できます。複素数の表現$-z^*n^2$と比べると、複素数では積が可換であることから、2つの$n$がまとまって$n^2$になっていると解釈できます。

八元数

八元数$o = a_0 + a_1e_1 + a_2e_2 + \dots + a_7e_7\ (a_i \in \mathbb{R})$に対して：

基底の2乗：$e_i^2 = -1\ (i = 1, \dots, 7)$
基底の積：$e_ie_j = e_k$（$i,j,k$が特定の巡回順序を満たす場合）
反交換性：$e_ie_j = -e_je_i\ (i \neq j)$
共役：$o^* = a_0 - a_1e_1 - a_2e_2 - \dots - a_7e_7$
ノルム：$|o| = \sqrt{oo^*} = \sqrt{a_0^2 + a_1^2 + a_2^2 + \dots + a_7^2}$
逆元：$o^{-1} = o^* / |o|^2\ (o \neq 0)$
実部：$\mathrm{Re}(o) = (o + o^*) / 2 = a_0$
虚部：$\mathrm{Im}(o) = (o - o^*) / 2 = a_1e_1 + a_2e_2 + \dots + a_7e_7$（基底を含む）

八元数$o_1,o_2,o_3$について、以下の性質が成り立ちます。

非可換性：一般に$o_1o_2 \neq o_2o_1$（特定の条件下で可換）
非結合性：一般に$(o_1o_2)o_3 \neq o_1(o_2o_3)$（特定の条件下で結合的）

特定の巡回順序は480種類あります。どれを採用しても代数的な性質は同じなため、本記事では古典的な定義を採用します。7shi-480

グレイブスとケイリーによる三つ組

$$ e_1e_2=e_3,\ e_1e_4=e_5,\ e_2e_4=e_6,\ e_3e_4=e_7,\ e_2e_5=e_7,\ e_3e_6=e_5,\ e_1e_7=e_6 $$

これら7種類の積の組み合わせのそれぞれを三つ組 (triad) と呼びます。実部と1つの三つ組に閉じた部分代数は四元数と同型で、結合性を満たします。

部分代数

$$ e_1e_2=-e_2e_1=e_3,\ e_2e_3=-e_3e_2=e_1,\ e_3e_1=-e_1e_3=e_2 $$

八元数（7次元）

八元数は7次元と8次元が扱えますが、使い勝手がかなり異なります。まず扱いが簡単な7次元について見ていきます。

7次元ベクトルと純虚八元数の同一視

$$ (x_1,x_2,\dots,x_7) \cong x_1e_1+x_2e_2+\dots+x_7e_7 $$

結合性に注意すれば、基本的には3次元の四元数の延長線上で扱えます。

内積

純虚八元数の内積は、純虚四元数と同じ形をしています：

純虚八元数の内積（7次元）

$$ v \cdot w = -\mathrm{Re}(vw) = -\frac12(vw+wv) $$

導出過程は、項が多いだけで四元数と同様のため省略します。計算過程に2項の積しか現れないため、非結合性による影響を受けません。

外積

純虚八元数の積の虚部は、特殊な空間構成により外積となります。7shi-ort

鏡映

7次元空間において、純虚八元数$v$を単位純虚八元数$n\ (n^2 = -1)$で定義される平面に関して鏡映で移した純虚八元数$v'$は以下の式で与えられます：

純虚八元数による鏡映（7次元）

$$ v'=-nv^*n=nvn $$

純虚四元数と同じ形をしています。導出も同様です。

$$ \begin{aligned} v' &= v - 2(v \cdot n)n \\ &= v + (vn + nv)n \\ &= v + vn^2 + nvn \\ &= nvn \end{aligned} $$

八元数の非結合性により、一般的には$(o_1o_2)o_3 \neq o_1(o_2o_3)$です。ただし八元数には交代性という弱い形での結合性があり、同一の八元数を2つ含む積においては$(vn)n=v(nn),(nv)n=n(vn)$が成り立ちます。そのため$nvn$では括弧を省略しています。wiki-alt nakajima

ただし、鏡映の合成では結合性が問題となるため、括弧を外すことはできません。例：$m(nvn)m$

非結合性の影響：

連続的な鏡映の合成（回転など）が複雑になる
代数的な性質の証明がより難しくなる
鏡映の基本的な性質（等長性、冪等性）は保たれる

四元数（4次元）

四元数は名前の通り4成分あるため、4次元を扱うことが可能です。ただし実部と虚部では性質が異なることから、その扱いはやや複雑となります。

4次元ベクトルと四元数の同一視

$$ (w, x, y, z) \cong w + xi + yj + zk $$

空間軸

四元数が表すのは4次元ユークリッド空間です。4番目の次元は空間軸であり、相対性理論のような時間軸ではありません。時間軸を含むミンコフスキー空間を扱うには、双曲四元数やクリフォード代数など別の代数系が必要となります。7shi-hc

内積

実部を含む四元数の内積を示します：

四元数の内積（4次元）

$$ \begin{aligned} v \cdot w &= \frac12(vw-wv+v^*w+vw^*) \\ &= \frac12\mathrm{Re}(v^*w + vw^*) \end{aligned} $$

2行目の方が式の形としては対称性がありきれいですが、鏡映の計算ではステップ数が増えるため、本記事では1行目を使用します。

四元数$v,w$を実部と虚部に分けます：

$$ v_r=\mathrm{Re}(v),\ v_i=\mathrm{Im}(v),\ w_r=\mathrm{Re}(w),\ w_i=\mathrm{Im}(w) $$

これを用いて内積を表現します：

$$ v \cdot w=v_rw_r-\frac12(v_iw_i+w_iv_i) $$

この形が得られる積の組み合わせを探します。

交換子と反交換子を確認します：

$$ \begin{aligned} vw-wv &=(v_r+v_i)(w_r+w_i)-(w_r+w_i)(v_r+v_i) \\ &=v_iw_i-w_iv_i \\ vw+wv &=(v_r+v_i)(w_r+w_i)+(w_r+w_i)(v_r+v_i) \\ &=2v_rw_r+2v_rw_i+2w_rv_i \end{aligned} $$

反交換子を参考に、不要な項が含まれないように、共役の付け方を工夫します：

$$ \begin{aligned} v^*w+vw^* &=(v_r-v_i)(w_r+w_i)+(v_r+v_i)(w_r-w_i) \\ &=2(v_rw_r-v_iw_i) \end{aligned} $$

これを交換子と足し合わせれば、内積の2倍が得られます。

$$ \begin{aligned} vw-wv+v^*w+vw^* &=v_iw_i-w_iv_i+2(v_rw_r-v_iw_i) \\ &=2v_rw_r-(v_iw_i+w_iv_i) \\ &=2(v \cdot w) \end{aligned} $$

なお、$v^*w+vw^*$の実部を取れば、別の表式が得られます。

$$ \mathrm{Re}(v^*w+vw^*) =2\left\{v_rw_r-\mathrm{Re}(v_iw_i)\right\} =2(v \cdot w) $$

鏡映

4次元空間において、四元数$q$を単位四元数$n\ (|n| = 1)$で定義される超平面に関して鏡映で移した四元数$q'$は以下の式で与えられます：

四元数による鏡映（4次元）

$$ q'=-nq^*n $$

$$ \begin{aligned} q' &=q-2(q \cdot n)n \\ &=q-(qn-nq+q^*n+qn^*)n \\ &=q-(qn-nq+q^*n)n-q|n|^2 \\ &=-(qn-nq+q^*n)n \\ \end{aligned} $$

$q^*n$の交換子から、交換後の形を確認します。

$$ \begin{aligned} q^*n-nq^* &=(q_r-q_i)(n_r+n_i)-(n_r+n_i)(q_r-q_i) \\ &=-q_in_i+n_iq_i \\ &=nq-qn \\ q^*n&=nq^*+nq-qn \end{aligned} $$

これを使って計算を続行します。

$$ \begin{aligned} q' &=-(qn-nq+q^*n)n \\ &=-(qn-nq+nq^*+nq-qn)n \\ &=-nq^*n \end{aligned} $$

3次元鏡映との関係

3次元鏡映（純虚四元数）：$v' = -nv^*n = nvn$
4次元鏡映（一般の四元数）：$q' = -nq^*n$

$q=v$とすれば一致するため、4次元鏡映は3次元鏡映を特殊ケースとして含みます。

7次元鏡映との関係

4次元鏡映（一般の四元数）：$q' = -nq^*n$
7次元鏡映（純虚八元数）：$v' = -nv^*n=nvn$

四元数の実部を八元数の$e_4$、虚部$i,j,k$を$e_1,e_2,e_3$に対応させます。

$$ w+xi+yj+zk \mapsto we_4+xe_1+ye_2+ze_3 $$

この対応によって、7次元鏡映は4次元鏡映を特殊ケースとして含みます。

鏡映は内積に依存しているため、内積の等価性から示せます。以下では$e_4$がどのように振舞うかの確認を兼ねて、実部と虚部に分けて成分計算します。

$$ \begin{alignedat}{2} v &= v_r + \underbrace{v_xi + v_yj + v_zk}_{v_i} &&\mapsto v_re_4 + \underbrace{v_xe_1 + v_ye_2 + v_ze_3}_{v_i} \\ n &= n_r + \underbrace{n_xi + n_yj + n_zk}_{n_i} &&\mapsto n_re_4 + \underbrace{n_xe_1 + n_ye_2 + n_ze_3}_{n_i} \\ \end{alignedat} $$

三つ組

本記事では$e_1e_2=e_3$の定義を採用しているため、$i,j,k$と$e_1,e_2,e_3$は代数として同型で、$v_i,n_i$の振る舞いは変換後も同一です。

$$ \begin{aligned} q' &=-(n_r+n_i)q^*(n_r+n_i) \\ &=-n_r^2q^*-n_rq^*n_i-n_iq^*n_r-n_iq^*n_i \\ &=-n_r^2(q_r-q_i)-n_r(q_r-q_i)n_i-n_i(q_r-q_i)n_r-n_i(q_r-q_i)n_i \\ &=-n_r^2q_r+n_r^2q_i-n_rq_rn_i+n_rq_in_i-n_iq_rn_r+n_iq_in_r-n_iq_rn_i+n_iq_in_i \\ &=-(n_r^2+n_i^2)q_r+n_r(q_in_i+n_iq_i)-n_r(2q_rn_i-n_rq_i)+n_iq_in_i \\ \end{aligned} $$
八元数では$n=n_re_4+n_i,\ v=q_re_4+q_i$として同様に計算します。$e_4$は$n_i$や$q_i$と反交換です。
$$ \begin{aligned} v' &=(n_re_4+n_i)v(n_re_4+n_i) \\ &=n_r^2e_4ve_4+n_re_4vn_i+n_ivn_re_4+n_ivn_i \\ &=n_r^2e_4(q_re_4+q_i)e_4+n_re_4(q_re_4+q_i)n_i+n_i(q_re_4+q_i)n_re_4+n_i(q_re_4+q_i)n_i \\ &=-n_r^2q_re_4+n_r^2q_i-n_rq_rn_i+n_rq_in_ie_4-n_iq_rn_r+n_iq_in_re_4-n_iq_rn_ie_4+n_iq_in_i \\ &=\{-(n_r^2+n_i^2)q_r+n_r(q_in_i+n_iq_i)\}e_4-n_r(2q_rn_i-n_rq_i)+n_iq_in_i \\ \end{aligned} $$
$e_4$の係数は実数になります。逆変換で$e_4 \mapsto 1$とすれば、四元数の計算結果と一致します。

八元数（8次元）

八元数は名前の通り8成分あるため、8次元を扱うことが可能です。実部と虚部では性質が異なりますが、四元数での4次元と同様に扱います。

8次元ベクトルと八元数の同一視

$$ (x_0,x_1,x_2,\dots,x_7) \cong x_0 + x_1e_1 + x_2e_2 + \dots + x_7e_7 $$

空間軸

八元数が表すのは8次元ユークリッド空間です。すべての次元は空間軸であり、相対性理論のような時間軸は含みません。時間軸を含むミンコフスキー空間を扱うには、分解型八元数やクリフォード代数など別の代数系が必要となります。

内積

八元数の内積は、四元数（4次元）と同じ形をしています：

八元数の内積（8次元）

$$ \begin{aligned} v \cdot w &= \frac12(vw-wv+v^*w+vw^*) \\ &= \frac12\mathrm{Re}(v^*w + vw^*) \end{aligned} $$

導出過程は、四元数と同様のため省略します。計算過程に2項の積しか現れないため、非結合性による影響は受けません。

鏡映

8次元空間において、八元数$o$を単位八元数$n\ (|n| = 1)$で定義される超平面に関して鏡映で移した八元数$o'$は以下の式で与えられます：

八元数による鏡映（8次元）

$$ o' = -no^*n $$

四元数（4次元）と同じ形をしています。非結合性の影響を受けないことにより、導出過程は四元数と同様のため省略します。

7次元鏡映との関係

7次元鏡映（純虚八元数）：$v' = -nv^*n = nvn$
8次元鏡映（一般の八元数）：$o' = -no^*n$

$o=v$とすれば一致するため、8次元鏡映は7次元鏡映を特殊ケースとして含みます。

クリフォード代数

これまでの章で現れた様々な次元での鏡映を統一的に理解する枠組みとして、クリフォード代数を導入します。

クリフォード代数$\mathrm{Cl}_{p,q}(\mathrm K)$は、体$\mathrm K$上のベクトル空間$V$に対して定義される代数系です。ベクトル空間の次元は$p+q$で、計量$1$の基底が$p$個、計量$-1$の基底が$q$個あります。基底の2乗は計量となります。

基底の2乗と計量

$$ e_i^2= \begin{cases} 1&(1 \le i \le p) \\ -1&(p+1 \le i \le p+q) \end{cases} $$

添え字

$\mathrm{Cl}_{p,q}(\mathrm K)$は英語版Wikipediaの表記法です。wiki-clifこの表記法は統一されておらず、異なる流儀があります。具体的には$p$が計量-1、$q$が計量1の基底の個数を表す場合があります。テキストによって異なるため、どのような流儀を採用しているか必ずご確認ください。

基底は反交換性$e_ie_j=-e_je_i\ (i \ne j)$を持ちます。基底の積はそのまま2次の基底として扱い、別の基底に変化することはありません。これはクリフォード代数が八元数とは異なる代数であることを意味しますが、複素数や四元数はクリフォード代数に含まれます。

代数の同型

$$ \mathrm{Cl}_{0,1}(\mathbb R)\cong\mathbb C,\quad \mathrm{Cl}_{0,2}(\mathbb R)\cong\mathbb H $$

四元数との対応

$e_1 \cong i,e_2 \cong j$とすれば$e_1e_2 \cong ij=k$となります。$e_1e_2$は2乗が$-1$となり、$e_1$や$e_2$と反交換性を持つため、四元数と同じ振る舞いをします。

$k^2 \cong (e_1e_2)^2=e_1e_2e_1e_2=-e_1e_1e_2e_2=-e_1^2e_2^2=-(-1)(-1)=-1$
$ik \cong \underbrace{e_1}_i\underbrace{e_1e_2}_k = -\underbrace{e_1e_2}_k\underbrace{e_1}_i \cong -ki,\ jk \cong \underbrace{e_2}_j\underbrace{e_1e_2}_k = -\underbrace{e_1e_2}_k\underbrace{e_2}_j \cong -kj$

クリフォード代数$a,b,c$について、以下の性質が成り立ちます。

非可換性：一般に$ab \neq ba$（特定の条件下で可換）
結合性：$(ab)c=a(bc)$

n次元ユークリッド空間は$\mathrm{Cl}_{n,0}(\mathbb R)$で扱います。

n次元ベクトルのクリフォード代数の表現

$$ (a_1,a_2,\dots,a_n) \cong a_1e_1 + a_2e_2 + \dots + a_ne_n $$

実用上、クリフォード代数は、3次元における四元数の振る舞いに基づいて、任意次元に拡張したものとなります。例えば8次元を扱う場合でも、八元数のような非結合性に煩わされる心配がありません。

3次元

3次元は$\mathrm{Cl}_{3,0}(\mathbb R)$となり、四元数と同型の$\mathrm{Cl}_{0,2}(\mathbb R)$とは異なる代数です。そのため細かい部分の符号などが四元数とは異なります。ただし、四元数のように3次元と4次元で計算方法が変わるようなことはなく、次元が変わっても使い勝手は基本的に同じです。

内積

クリフォード代数の内積は、純虚四元数と似た形をしていますが、符号が異なります：

クリフォード代数の内積

$$ v \cdot w = \frac12(vw+wv) $$

$$ \begin{aligned} vw &=(v_1e_1+v_2e_2+\dots+v_ne_n)(w_1e_1+w_2e_2+\dots+w_ne_n) \\ &=v_1w_1+v_2w_2+\dots+v_nw_n \\ &\quad+(v_1w_2-v_2w_1)e_1e_2+(v_2w_3-v_3w_2)e_2e_3+\dots+(v_{n-1}w_n-v_nw_{n-1})e_{n-1}e_n \\ wv &=(w_1e_1+w_2e_2+\dots+w_ne_n)(v_1e_1+v_2e_2+\dots+v_ne_n) \\ &=w_1v_1+w_2v_2+\dots+w_nv_n \\ &\quad+(w_1v_2-w_2v_1)e_1e_2+(w_2v_3-w_3v_2)e_2e_3+\dots+(w_{n-1}v_n-w_nv_{n-1})e_{n-1}e_n \end{aligned} $$
$$ \therefore vw+wv=2(v_1w_1+v_2w_2+\dots+v_nw_n)=2(v \cdot w) $$

クリフォード代数では基底が付かない実部に相当する部分をスカラーと呼びます。

ウェッジ積

$vw$のスカラー以外の部分は、基底についての2次式となります。これは任意次元に拡張した外積で、ウェッジ積と呼ばれる演算に相当します。

鏡映

任意次元のクリフォード代数において、ベクトル$v$を単位ベクトル$n\ (n^2 = 1)$で定義される超平面に関して鏡映で移したベクトル$v'$は以下の式で与えられます：

クリフォード代数による鏡映

$$ v'=-nvn $$

クリフォード代数の式、任意の次元で統一的に成り立ちます。純虚四元数と似た形をしていますが、符号が異なります。

$$ \begin{aligned} v' &= v - 2(v \cdot n)n \\ &= v - (vn+nv)n \\ &= v - vn^2 - nvn \\ &= -nvn \end{aligned} $$

四元数との比較

四元数における3次元鏡映$v'=nvn$と比較すれば符号が異なります。4次元鏡映$q'=-nq^*n$と比較すれば共役がありません。

まとめ

次元が上がるにつれて鏡映の式は以下のように変化しました：

ベクトル：$\mathbf{v}' = \mathbf{v} - 2(\mathbf{v} \cdot \mathbf{n})\mathbf{n} = (I - 2\mathbf{n}\mathbf{n}^{\mathsf T})\mathbf{v}$
複素数 (2D)：$z' = -nz^*n = -z^*n^2$
四元数 (3D)：$v' = -nv^*n = nvn$
八元数 (7D)：$v' = -nv^*n = nvn$
四元数 (4D)：$q' = -nq^*n$
八元数 (8D)：$o' = -no^*n$
クリフォード代数：$v' = -nvn$

別記事にまとめる予定ですが、2回の鏡映の合成は回転になります：

複素数 (2D)：$-m(-nz^*n)^*m = z(n^*m)^2$（鏡映を経由しなくても、積自体が回転）
四元数 (3D)：$-m(-nv^*n)^*m = mnvnm$
八元数 (7D)：$-m(-nv^*n)^*m = m(nvn)m$（非結合性により括弧は外せない）
四元数 (4D)：$-m(-nq^*n)^*m = mn^*qn^*m$
八元数 (8D)：$-m(-no^*n)^*m = m(n^*on^*)m$（非結合性により括弧は外せない）
クリフォード代数：$-m(-nvn)m = mnvnm$

クリフォード代数は、これらの代数系での鏡映表現を統一的に扱う枠組みを提供します。これにより、任意の次元での鏡映や回転を一貫した方法で記述することが可能になります。

この性質は、以下の分野で重要な役割を果たします：

群論：鏡映の合成が回転群を生成
量子力学：スピンの概念との関連
コンピュータグラフィックス：3D回転の効率的な実装
ロボット工学：関節動作の表現

線対称な鏡映

通常の鏡映とは符号を反転した式は、$\mathbf n$が表す直線に対して線対称な鏡映となります。

線対称な鏡映

ある対象をある直線に関して反転させる幾何学的操作

ベクトル$\mathbf{v}$を単位ベクトル$\mathbf{n}$で定義される線対称な鏡映で移したベクトル$\mathbf{v}''$は以下の式で与えられます：

線対称な鏡映

$$ \begin{aligned} \mathbf{v}'' &= \mathbf{v} + 2\{(\mathbf{v} \cdot \mathbf{n})\mathbf{n} - \mathbf{v}\} \\ &= 2(\mathbf{v} \cdot \mathbf{n})\mathbf{n} - \mathbf{v} \\ &= -\mathbf{v}' \end{aligned} $$

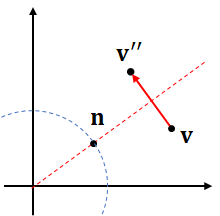線対称な鏡映