文献あり

量子情報とHaar測度

554

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

はじめに

はじめてまして、理物B2のぴろしきです。色々な分野をつまみ食いしています。今回はPhysics Labのアドベントカレンダー企画の一環で初めて記事を執筆しました。この記事では、個人的に興味を持っている量子情報におけるランダムネスの話に簡単に触れていきたいと考えています。
ところどころ厳密じゃないところがあると思いますが物理数学の記事ということでご容赦ください。

数学的な準備

Haar測度とは

まず最初に今回のトピックとなるHaar測度について紹介しようと思います。

（左）Haar測度

$G$を局所コンパクト群、$B$をGのコンパクト集合全体から生成される完全加法族とする。この時測度空間($G$,$B$)上の確率測度$\mu$であって以下の条件を満たすものを（左）Haar測度という。

$G$の元$g$による左移動作用に関して任意の$G$の部分集合$S$の測度は不変である。すなわち$\mu(g(S))=\mu(S)$を満たす。

（左）Haar測度と書きましたが、右の場合は右移動作用に関して成り立てば良いです。これはどのようなモチベーションに基づいたものなのか考えてみます。
まず普通の$\mathbb{R}^n$に対するルベーグ測度を思い出してみます。その時にルベーグ可測集合$A$に並行移動$A+x$を施してもルベーグ可測集合でありかつ測度が等しいというものがあったと思います。これを一般化したものがHaar測度になってくれていれば嬉しいですね。定義1に出てきた局所コンパクト群というのは以下の性質を持つものでした。（本質的なところじゃないので飛ばしてOKです）

局所コンパクト空間

位相空間$X$が局所コンパクトであるとは、任意の点$x\in X$ に対して、$x$の$X$における近傍$U$でコンパクトなものが存在することである。

位相群

位相空間$X$が位相群であるとは、$X$に定義される群演算が連続になることである。

ハウスドロフ空間

位相空間$X$がハウスドロフ空間であるとは、任意の2点$x,y\in X$について各点のある近傍$U_x,U_y$があって$U_x\bigcap U_y= \varnothing$であることである。

実際$\mathbb{R}^n$は以上の性質を満たしています。この時に群演算として普通の足し算を考え、$\mathbb{R}^n$の左移動作用を考えれば、Haar測度の定義がルベーグ測度に一致していることがわかります。
今回の文脈においては量子状態の存在するヒルベルト空間と作用となるユニタリオペレーターに対してHaar測度を入れたいので、以下のような形で扱って行きます。

Haar測度(for 量子物理)

$H$をヒルベルト空間とし、$H$に作用するユニタリ群を$U(H)$とする。この時確率測度$\mu$であって、以下の条件を満たすものをHaar測度という。

$U(H)$の可測な部分集合$w$と$U(H)$の元$u$に対して
$\mu(uw)=\mu(wu)=\mu(w)$を満たす。

例えばユニタリ群$U(1)$について考えてみましょう。$U(1)$は複素平面上の単位円とみなすことができますが、もし単位円上の確率測度が不規則に分布しているとしたらどうでしょう。ある$U(1)$の元を全体に作用させれば、それは分布をぐるっと回すことに相当するので測度は変化してしまいます。一方で一様に分布しているとすればぐるっと回しても測度は変わらないですね。というわけで$U(1)$上のHaar測度としては一様分布を考えることができるわけです。
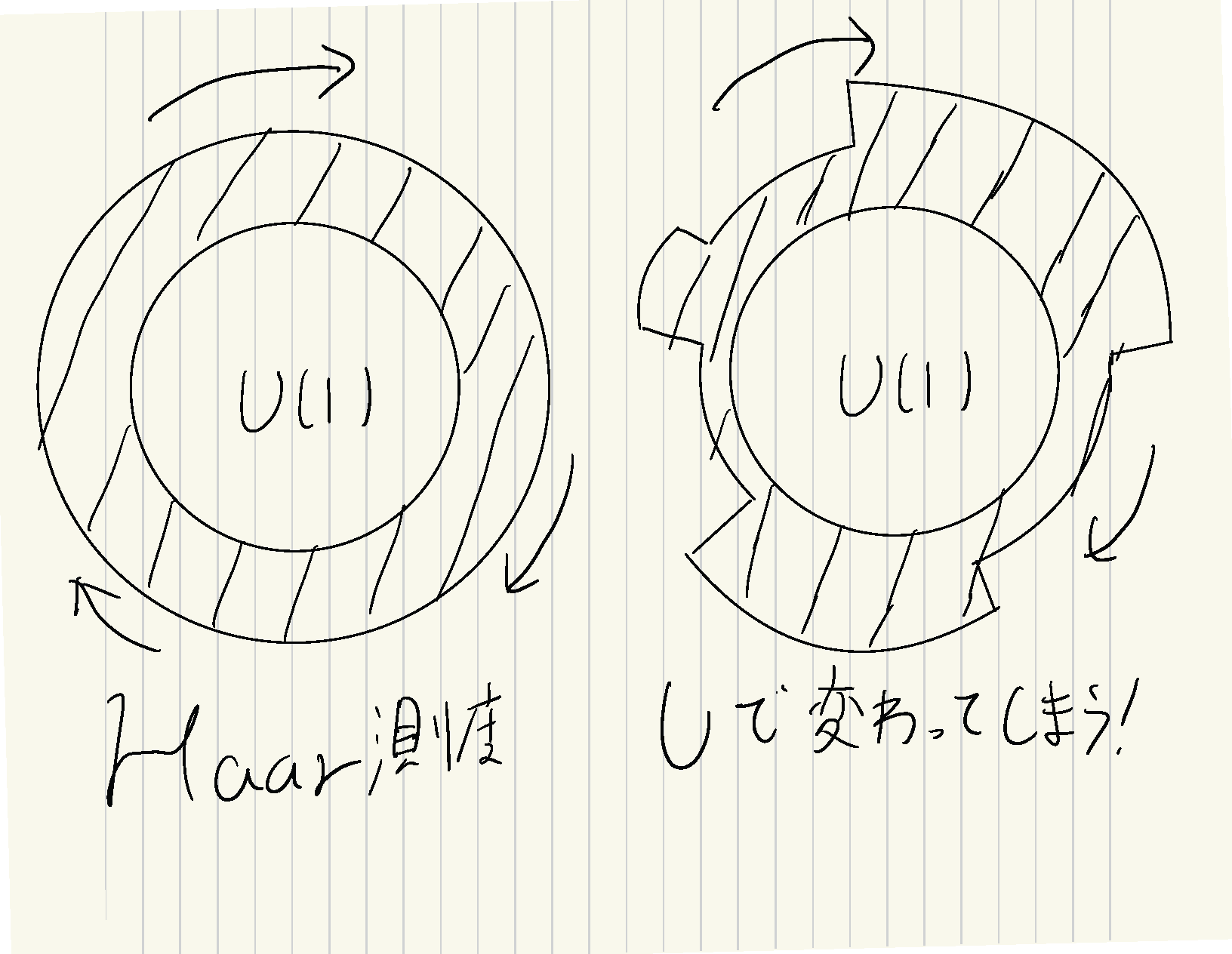Haar測度のイメージ
Haar測度は定数倍を除いて一意に定まる性質を持ちます。以下ではHaar測度を平均を取る場面で多く使っていくので、全域での積分値が1となるように取っているものとします。また与えられた測度$\mu$に従う積分を $\int \mu(dU)$というように表現します。

Unitary t-design

上で紹介したHaar測度とそれによって生まれるランダムネスは量子情報における解析で非常に有用ですが、実装が困難であることが知られています。そこでこれを近似したUnitary designという概念を導入します。

Unitary t-design

$t\in\mathbb{Z^+}$においてユニタリ群$U(H)$上の集合$U’=\{U_k\}$が
$\int \mu(dU)(U^{\otimes t}M(U^{\otimes t}))=\frac{1}{K}\sum_k (U_k^{\otimes t}M(U_k^{\otimes t}))$
を満たすとき$\mu'$をUnitary t-designと呼ぶ。
なお、$K$は$U’$の要素の数とする。

この定義によれば、テンソル積の回数が等しいならHaar測度で成立したことをそのまま適応することができます。
有名なUnitary 2-design(3-designでもある)としてクリフォードゲートがあります。

パウリ群

パウリ演算子$\{I,X,Y,Z\}$のテンソル積とその符号$\{\pm1,\pm i\}$の直積によって表される集合$\{\pm1,\pm i\}\times \{I,X,Y,Z\}^{\otimes n}$をパウリ群と呼ぶ。

クリフォードゲート

パウリ群$P^{\otimes n}$の任意の元$p$に対する作用$c$であって
$cpc^\dagger\in P$
を満たすものを(n-qubit)クリフォードゲートという。

ちょっと抽象的ですね。例えば、1qubitの場合を考えてみると、
$\{\pm1,\pm i\}\times \{I,X,Y,Z\}$に対するクリフォードゲートはパウリゲートに加えてアダマールゲート$H=\frac{1}{\sqrt{2}}\left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right) $位相ゲート$S=\left( \begin{array}{cc} 1 & 0 \\ 0 & i \end{array} \right)$を用いて以下のように表せます。
$\{I,H,S,HS,SH,HSH \}\times \{I,X,Y,Z\}$
つまり24個あるということになりますね。この上の一様分布を考えてあげれば、Unitary designとなり、ある種のHaar測度の近似になるわけです。
この点についてはAnaの最後の方で詳しく扱われています。

Schurの補題

次に、表現論という分野で基本的な性質として使われる、Schurの補題について紹介します。まずは表現論とは何かというところからざっくり話していきましょう。
以下で単に群といったら有限群のことを指すとします。

（群の）表現

$V$をベクトル空間とし、$GL(V)$で$V$上の可逆な線形写像の全体（一般線形群）を表す。このとき、群の準同型$\rho:G\rightarrow GL(V)$を$G$の$V$ 上の表現と呼ぶ。$V$を表現空間と呼ぶ。
（名古屋より）

今後このような表現を、群準同型$\rho$と表現空間$V$のペア$(\rho,V)$で表します。

表現の同型

表現$(\rho,V)$と$(\rho',V')$が同型であるとは、以下の性質を満たすことを指す。
$G$の任意の元$x$に対してある同型写像$\sigma:V\rightarrow V'$が存在して
$\sigma\circ \rho(x)= \rho'(x)\circ \sigma$
が成立する。

要するに可換な図式が書ければ良いということになります。
次に証明の肝となる不変部分空間について紹介します。

不変部分空間と規約な表現

$G$の表現$(\rho,V)$について、$W\in V$が$\rho$の不変部分空間であるとは、以下の性質を満たすことを指す。
$G$の任意の元$x$について$ \rho(x)(W)\subseteq W$が成立する。
また表現$(\rho,V)$が自明でない不変部分空間を持たない時、規約な表現と呼ぶ。

これはつまり、部分空間$W$の元を$\rho(x)$で写した先も$W$に入っていることを指しています。また自明な不変部分空間というのは$V$全体もしくは$\{0\}$のみの空間を指します。
以上の定義をもとにSchurの補題を示していきます。

Schurの補題

群$G$と規約な表現$(\rho,V)$と$(\rho',V')$に対し、$G$の任意の元$x$に対してある線型写像$\sigma:V\rightarrow V'$が存在して
$\sigma\circ \rho(x)= \rho'(x)\circ \sigma$
が成立するならば、$\sigma$は零写像であるか、同型写像である。

零写像の場合は明らかなので、零写像でなければ同型写像であることを示す。
まず$\sigma$が単射であることを示す。$\sigma$の核$\ker\sigma=\{x∈V|\sigma(x)=0\}$ を考えると、$\ker\sigma$ の任意の元$K$と $G$の任意の元$x$に対して$\sigma\circ \rho(x)(K)= \rho'(x)\circ \sigma(K)=0$が成り立つので、$\rho(x)(K)\in \ker\sigma$ である。よって$\ker\sigma$は$\rho$で不変である。$\rho$は既約であったから$\ker\sigma=\{0\},V$でなければならない。前者ならば$\sigma$は。単射一方後者ならば$\sigma$は零写像。
次に$\sigma$が全射であることを示す。$\sigma$の像 $\sigma(V)=\{\sigma(v)|v∈V\}$ を考えると、$G$の任意の元$x$に対して $\sigma\circ \rho(x)(V)= \rho'(x)\circ \sigma(V)$ なので、$\sigma(V)$ は$\rho'(x)$で不変である。$\rho'(x)$は既約であるので、$\sigma(V)=\{0\},V'$。前者ならば$\sigma$は零写像。一方後者ならば$\sigma$は全射。
よって零写像でなければ同型写像であることが示された。

この補題から重要な系が導出されます。

上の条件で、$V=V',\rho=\rho'$であるとき、$\sigma$はベクトル空間の係数体の代数閉体$R$の元$r$を用いて$\sigma=r\circ id_V$と表せる。

$V$に対する$\sigma$の固有値を$r$とすれば、これは$R$に含まれる。
$\delta=\sigma-r\circ id_V$とおいて、この写像が零であることを示す。
$G$の任意の元$x$に対して$\delta\circ \rho(x)= \rho(x)\circ \delta$が成立することは、簡単に確かめられる。
ここでSchurの補題より$\delta$は同型写像か零写像であるが、もし同型写像であるとすると、$r$の固有ベクトル$v\ne0$について、
$\delta(v)=(\sigma-r\circ id_V)(v)=(r-r)=0$
となってしまい、$0$でない元が$0$に写ってしまい、矛盾。
よって$\delta$は零なので、$\sigma=r\circ id_V$

これにより、表現の不変部分空間に対する同型写像は、スカラー倍の作用の形で書けることがわかります。

以上が数学的なイントロダクションでした。次の章では量子情報の文脈で具体的にどのように生きてくるのか見ていきたいと思います。

量子情報への応用

この章ではHaarランダムの量子情報への応用として乱択ベンチマーキングと呼ばれる、量子ノイズを推定する手法を紹介します。
量子系のユニタリ時間発展は、現実ではノイズが乗ることが避けられません。しかしながらノイズによって測定が変化したとしても、そもそも量子系自体確率的なものである以上、それがどう変化したのかを判断することは不可能に近いです。ここではいくつかの仮定を置いた上で、ノイズがどう量子ゲートに影響を及ぼしたのかを考察していきます。
なお、この記事ではJosephで紹介されている手法を参考に説明していますが、中田でも、置換ユニタリを用いて少し異なる議論が展開されています。

量子測定の基礎

射影測定

まずは射影測定と呼ばれる測定方法について説明します。今量子状態がベクトル$\ket{\phi}$で表されていて、以下で定義される射影演算子$\hat{P}=\{\hat{P_1},\hat{P_2},\dots,\hat{P_k}\}$によって測定を行うことを考えましょう。

射影演算子

$\hat{P}=\{\hat{P_1},\hat{P_2},\dots,\hat{P_k}\}$は以下の条件を満たすとき射影演算子と呼ばれる。

$P_i$は半正定値である。
$P_i$は冪等である。すなわち$P_i=(P_i)^2$
$P_i$は直行である。すなわち$P_iP_j=0(i\ne j)$
$P_i$は規格化されている。すなわち$\sum_i P_i=1$

これらを用いて測定を行ったときに、例えば$P_i$に対応する固有値$a_i$を得る確率$p(a_i)$は、
$p(a_i)=\bra{\phi}P_i\ket{\phi}$となり、また射影測定後の状態$\ket{\phi'(a_i)} $は、
$\ket{\phi'(a_i)}=\frac{P_i\ket{\phi}}{\sqrt{p(a_i)}}$
となります。ここで$\sqrt{p(a_i)}$は$\bra{\phi'(a_i)}\ket{\phi'(a_i)}=1$を満たすための規格化定数です。
射影測定は、状態が射影演算子の固有空間に落ちるため、何度同じ測定をやっても、出てくる値が等しいということで理想的な測定と呼ばれます。

POVM

一方でいつもこのように測定ができるとは限りません。例えば測定に誤差が発生したり、測定時に状態が固有空間に落ちない場合などは別の考え方をする必要があります。そこで出てくるのが間接測定です。間接測定では、実際の系を直接測定する代わりに、プローブと呼ばれる観測用の系を別に用意し、それをシステムと相互作用させて、プローブを測定することでシステムの状態を計算するという手法を取ります。
まずシステムとプローブの初期状態をそれぞれ$\ket{\phi},\ket{\Phi}$とおけば、その合成系は$\ket{\phi}\ket{\Phi}$と表されます。この状態に適当なユニタリ時間発展$\hat{U}$を作用させ、システムとプローブに相関を持たせます。最後にプローブに対してプローブの正規直交基底$\{\ket{\Psi_k}\}$を用いて射影演算子$\{\ket{\Psi_k}\bra{\Psi_k}\}$を作り、射影測定を行います。
数式で流れを追うと以下のようになります。
$\ket{\phi}\ket{\Phi}\rightarrow\hat{U}\ket{\phi}\ket{\Phi}\rightarrow(測定後の状態)=\frac{(1\otimes\ket{\Psi_k}\bra{\Psi_k})\hat{U}\ket{\phi}\ket{\Phi}}{\sqrt{p(a_k)}}$
ここでクラウス演算子を導入します。

クラウス演算子

上の例で
$p(a_k)=\bra{\phi}\bra{\Phi}\hat{U^\dagger}(\ket{\Psi_k}\bra{\Psi_k})\hat{U}\ket{\phi}\ket{\Phi}$
となる。ここで内部のプローブにかかるところだけまとめることで
$\norm{\bra{\Psi_k}\hat{U}\ket{\Phi}\ket{\phi}}^2$とできる。（システムとプローブの場所を変えた。）
ここで$\bra{\Psi_k}\hat{U}\ket{\Phi}$をシステムにかかる演算子としてクラウス演算子$Q_k$と呼ぶ。

このクラウス演算子は規格化条件を満たしています。実際kについて和を取ると、
$\sum_k\bra{\Phi}\hat{U^\dagger}\ket{\Psi_k}\bra{\Psi_k}\hat{U}\ket{\Phi}=\bra{\Phi}\hat{U^\dagger}\hat{U}\ket{\Phi}=1$となります。
ここで今上に書いた$\bra{\Phi}\hat{U^\dagger}\ket{\Psi_k}\bra{\Psi_k}\hat{U}\ket{\Phi}=\hat{M_k}$をPositive operator-valued measure(POVM)と呼びます。POVMの性質として以下のようなものがあります。

POVMの性質

POVM$\hat{M}=\{\hat{M_1},\hat{M_2},\dots,\hat{M_k}\}$は以下の条件を満たす。

$M_i$は半正定値である。
$M_i$は規格化されている。すなわち$\sum_i M_i=1$

実際上で作ったPOVMはこれらの条件を満たしていますね。
最後に量子ゲートの内積の定義について書いておきます。

量子ゲートの内積

任意の量子ゲート$N$と、作用するヒルベルト空間$H$について$\Tr(N)$を以下のように定義する。$H$の正規直交基底を$\{\ket{\phi_i}\}$とすれば
$\Tr(N)=Tr(\bra{\phi_i}N(\ket{\phi_i}\bra{\phi_j})\ket{\phi_j})$

この章の議論から、間接的な測定についても、クラウス演算子によって測定に伴うシステムの状態変化を見ることができ、その結果を得る確率はPOVMによって計算することができました。以下の節ではシンプルな$(0,1)$のみのPOVMを使って、測定を行っていきます。

乱択ベンチマーキングの手法

まずはノイズに対して以下の仮定を置きます。

ユニタリ時間発展$U$に対して、ノイジーな量子ゲートを$G_U$とする。この時$G_U$はユニタリ時間発展を表す$U$と量子ノイズ$N_U$の合成になる。
すなわち$G_U=N_U\circ U$となる。
また量子ノイズ$N_U$は量子ゲートの種類に依存しない。

一つ目の仮定に対する物理的な意味を考えると、ノイズが影響を及ぼす時間よりも量子ゲートの実装にかかる時間の方が十分小さい時にこのような形になることが推察されます。また二つ目の仮定については、各ユニタリに依存しない背景ノイズに対する推定と見做せます。
ここで量子状態の忠実度という概念を考えます。

忠実度

量子状態の密度演算子$\rho,\sigma$がある時
$F(\rho,\sigma):=\biggl(\Tr(\sqrt{\sqrt{\sigma}\rho\sqrt{\sigma}})\biggr)^2$
を$\rho,\sigma$の忠実度という。

これには例えば純粋状態$\rho=\ket{\phi}\bra{\phi},\sigma=\ket{\psi}\bra{\psi}$を入れてみれば内積の二乗になり、片方のみなら$ \bra{\psi}\rho\ket{\psi}$と量子状態に対する純粋状態による測定の期待値を表す量になります。どちらにせよこれが2つの状態の"近さ"みたいなものを意味していると思ってもらえればOKです。

ある量子ゲート$N$が$\ket{\phi}\bra{\phi}$に作用して、$N(\ket{\phi}\bra{\phi})$となることを考えます。もしこの状態$\ket{\phi}\bra{\phi}$がHaar測度にしたがってランダムに選ばれるとした時、$\ket{\phi}\bra{\phi}$と$N(\ket{\phi}\bra{\phi})$の忠実度の期待値を考えることができます。これを平均忠実度と言います。

平均忠実度

量子チャンネル$N$とHaar測度$\mu$について、
$\tilde{F}(N):=\int \mu(d\phi)F(\ket{\phi}\bra{\phi},N(\ket{\phi}\bra{\phi}))/\int \mu(d\phi)$
を平均忠実度という。

ここでさっき出てきた量子ノイズ$N_U$の平均忠実度を測ってみることにすると、Haar測度のユニタリ作用不変性を利用して
$\tilde{F}(N_U)=\int \mu(d\phi)F(\ket{\phi}\bra{\phi},N_U(\ket{\phi}\bra{\phi})) =\int \mu(d\phi)F(U\ket{\phi}\bra{\phi}U^\dagger,N(U\ket{\phi}\bra{\phi}U^\dagger))=\int \mu(d\phi)F(U\ket{\phi}\bra{\phi}U^\dagger,G_U(\ket{\phi}\bra{\phi}))$
となります。これが意味していることは、量子ノイズの平均忠実度が理想的な量子ゲートとノイジーな量子ゲートとの間の平均忠実度と等しくなっているということです。
この平均忠実度に関する以下の定理を提示しておきましょう。こちらの証明は省略しますがNielsenで示されれています。

平均忠実度とクラウス演算子

量子チャンネル$N$、ヒルベルト空間$H$の次元$d$を用いて平均忠実度を以下のように書ける。
$\tilde{F}(N)=\frac{d+\Tr[N]}{d(d+1)}$

ここで以下のようなアルゴリズムを与えます。

乱択ベンチマーキングのアルゴリズム

初期状態$\rho_{ini}$、POVM $\hat{M}=\{\hat{M_0},\hat{M_1}\}$、整数$m>0$をとる。
Haar測度$\mu$に従って$m$個のユニタリ$u_1,u_2,\dots,u_m$(対応するノイズレスなゲートは$U_1,U_2,\dots,U_m$)をランダムに選ぶ。この選び方に$A$と名前をつける。これらのゲートは$U_i(\rho)=u_i\rho u_i^\dagger$というように作用する。
これらに対応する実際のゲート（ノイズがのってる）$G_1,G_2,\dots,G_m$を順番に$\rho$に作用させる。

$U_1,U_2,\dots,U_m$の合成に共役なノイズつきゲート$N_U\circ U_1^\dagger\circ U_2^\dagger\dots U_m^\dagger$を作用させる。（この結果できた状態を$\rho_{out}$とする。）
結果をPOVMで測定し、$0,1$の結果を得る。
POVMを繰り返すことで測定結果$0$を得る確率
　$p_0(m,A)=\Tr[\hat{M_0}(\rho_{out})]$
を推定する。
さらに選び方AについてHaar測度に基づいた平均をとる。
$p_0(m)=\int \mu(dA)p_0(m,A)$
以上のプロセスを色々な値の$m$で行う。

これがなぜノイズの評価につながるのでしょうか？ポイントとなるのは色々な$m $で、違った$p_0(m)$が出てくるところです。もし量子ゲートにノイズがのっていなければ、以上の操作はただ元の状態に戻すだけのものになるので$p_0(m)=\Tr[M_0(\rho)]$に固定されます。しかし、ノイズのある状態では回数が増えるほどノイズによる影響が広がって、$p_0(m)$の値に差が生まれます。
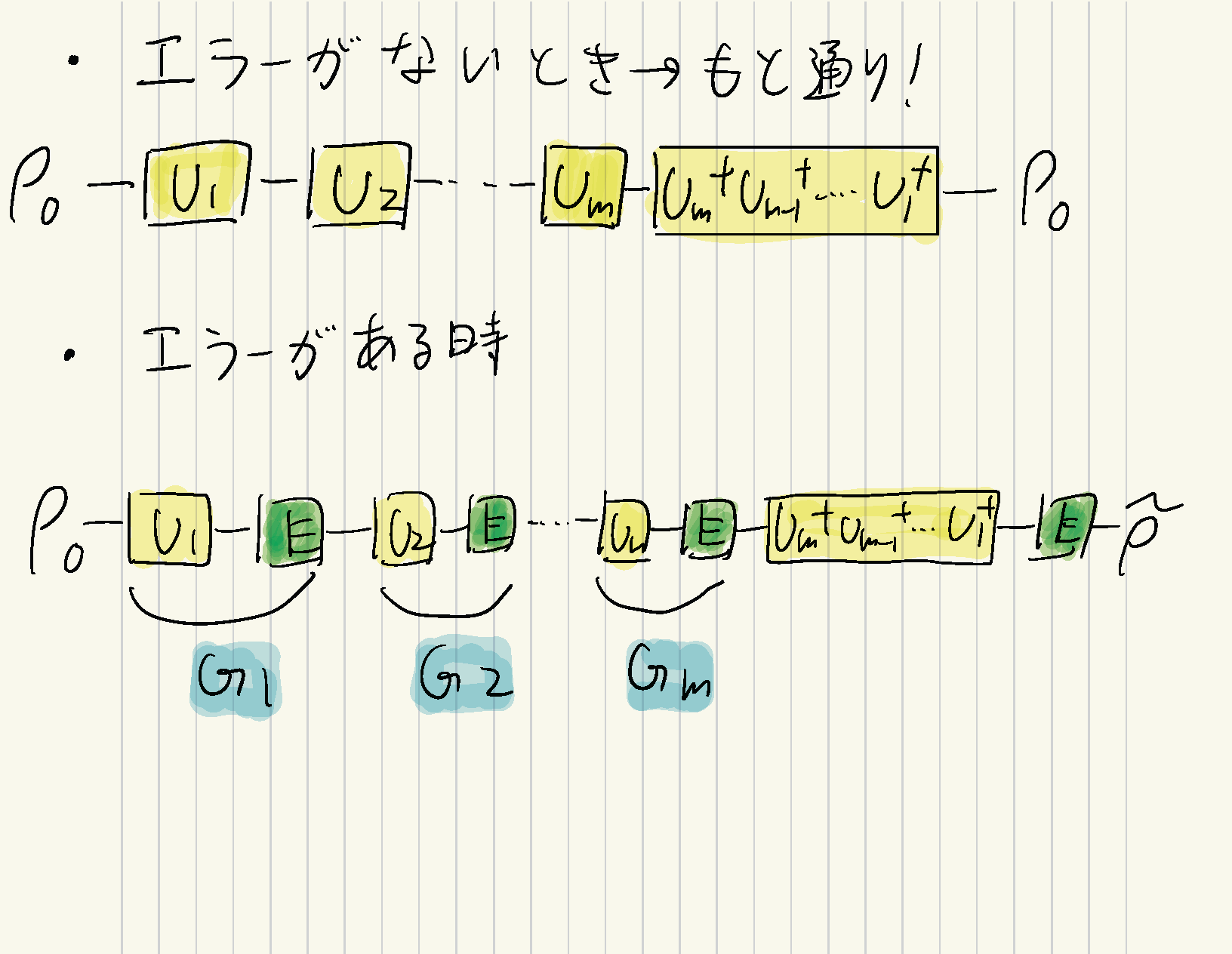エラーの影響のイメージ
というわけで、この$p_0(m)$からさっき出てきた平均忠実度とかを求められたらすごく都合がいいわけですが、ちょうどそんな定理が示せます。

忠実度の計測

量子ノイズ$N_U$がある状態で、$p_0(m)$は$m$に依存しない2数$a,b$、忠実度パラメーター$f(N_U)=\frac{d\tilde{F}(N_U)-1}{d-1}$を用いて以下のように表すことができる。
$p_0(m)=a+bf(N_U)^m$
ただし$d$は量子系の次元とする。

まず$\rho$に作用する量子ゲートをまとめてみる。
$G_{total}=N_U\circ U_1^\dagger\circ U_2^\dagger\dots U_m^\dagger\circ N_U\circ U_m\dots N_U\circ U_2\circ N_U\circ U_1 $
ここで$U_n'= \prod_{i=1}^{n} U_i$というユニタリを実装すると、
$U_n= \prod_{i=1}^{n} U_i(\prod_{i=1}^{n-1} U_i)^\dagger=U_n'(U_{n-1}')^\dagger $とできるので、これを元に
$G_{total}(\rho)=N_U\circ (U_m'^\dagger\circ N_U\circ U_m')\dots (U_2'^\dagger\circ N_U\circ U_2')\circ (U_1'^\dagger\circ N_U\circ U_1')(\rho) $
と変形できる。
今一つ一つの$(U_m'^\dagger\circ N_U\circ U_m')$に注目してみる。これは実際に状態$\rho$に作用するときのことを考えると
$U_m'^\dagger\circ N_U\circ U_m'=(U_m\circ U_{m-1}\dots U_1)^\dagger\circ N_U\circ(U_m\circ U_{m-1}\dots U_1)$となるが、今各ユニタリはHaar測度に従って選ばれていたことを思い出そう。Haar測度のユニタリ不変性から、$U_m'^\dagger\circ N_U\circ U_m'$の作用の平均は$m$の値に関わらず一致する。この値を$N_{av}$とする。
以上より$\int \mu'(dU)G_{total}=N_U\circ (N_{av})^m$なので、$p_0(m)$はより簡単な形で
$p_0(m)=\Tr[\hat{M_0}N_U\circ (N_{av})^m(\rho_{ini})]$
と書ける。ここで$\rho_{m-1}=(N_{av})^{m-1}(\rho_{ini})$と置いておく。
今$N_U$と任意の$U'_m $が可換であったことから、状態空間を表すd次元行列空間$Md$を部分空間
$Md=M_cd\oplus M_0d, M_0d=[X∈Md;TrX=0], M_cd=[単位行列のc倍]$
に分ければ、それぞれがユニタリ作用で不変であることがわかる。そのため、Schurの補題を思い出すと$N_{av}$はこれらの部分空間に対してそれぞれスカラーとして作用するはずだから、同様にトレースレスの部分と単位行列の$\Tr[\rho_{m-1}]$倍の要素に$\rho_{m-1}=\rho_{m-1:0}\oplus \rho_{m-1:\Tr[\rho_{m-1}]}$と分解すれば
$ N_{av}(\rho_{m-1})=\lambda_1\rho_{m-1:0}+\frac{\lambda_2}{d} \rho_{m-1:\Tr[\rho_{m-1}]}$となる。
まず1点目として、ノイズが状態空間の間の作用であることを加味すると、トレース保存性を持っていて、$\lambda_2=1$である。また、$\Tr[N_{av}]=\sum_{i,j}\bra{\phi_i}N_{av}(\ket{\phi_i}\bra{\phi_j})\ket{\phi_j}$を用いれば、
$\lambda_1=\frac{\Tr[N_{av}]-1}{d^2-1}$
$\Tr[N_{av}] $は$N_{av} $のユニタリ不変性から、$\Tr[N_U]$と等しい。
ここで定理4を用いて整理すると、$f(N_U)=\frac{\Tr[N_U]-1}{d^2-1}$より、
$p_0(m)=f(N_U)\Tr[\hat{M_0}N_U\rho_{m-1}]+(1-f(N_U))\Tr[\frac{\hat{M_0}N_U}{d}]$
と書ける。これは$m$に依存しない変形だったので、$\Tr[\hat{M_0}N_U\rho_{m-1}]$に何度も同じ変形を施して展開していくと
$p_0(m)=f(N_U)^m\Tr[\hat{M_0}N_U\rho_{ini}]+(1-f(N_U)^m)\Tr[\frac{\hat{M_0}N_U}{d}]=f(N_U)^m\Tr[\hat{M_0}N_U\rho_{ini}-\frac{\hat{M_0}N_U}{d}]+\Tr[\frac{\hat{M_0}N_U}{d}]$
となる。係数は$m$に依存していないので、$p_0(m)=a+bf(N_U)^m$の形で表せた。

今、Haar測度で与えたユニタリーを用いて証明を行いましたが、実はこの議論はunitary 2-designでも成り立つことが知られています。そのため、実際にはクリフォードゲートを用いて実験が行われています。また、今回Schurの補題を用いて計算をした部分は、Twirling（トワリング）と呼ばれる操作に対応しています。
これでこの記事のメインの部分は終了です！最後に論文を読んでいて気になったことや、近年の話について調べたことを軽くまとめておきます。

今後の課題

今回紹介した乱択ベンチマーク（RBと書きます）の手法は試行回数が少なくても良い精度が出る一方で使用するUnitary designを量子的にどう作成するかという点で課題を抱えています。
例えば、詳しい定義は載せませんが、RawadではUnitary Designに対して、$\epsilon$程度の誤差を認めたUnitary t-designが、qubitの数と$t$の多項式時間で作成可能であることに触れています。
また、そもそもの構造として、今回紹介したRBは不十分であるという指摘もあります。例えばAnaで解説されている同時RBでは2つの系を用意し、それぞれの系で通常のRBを行ったのち、両者で同時にRBを実行することで、平均忠実度に止まらない測定結果の獲得や、RBを行うことによる互いへの影響などをみることができるようです。
今後量子技術が実用に近づくにつれ、量子ゲートの特徴を評価できる今回のような分野は発展していくことが期待されます。今後も様々な手法とその背後の数理に取り組んでいきたいと思います。