文献あり

商空間の例

2065

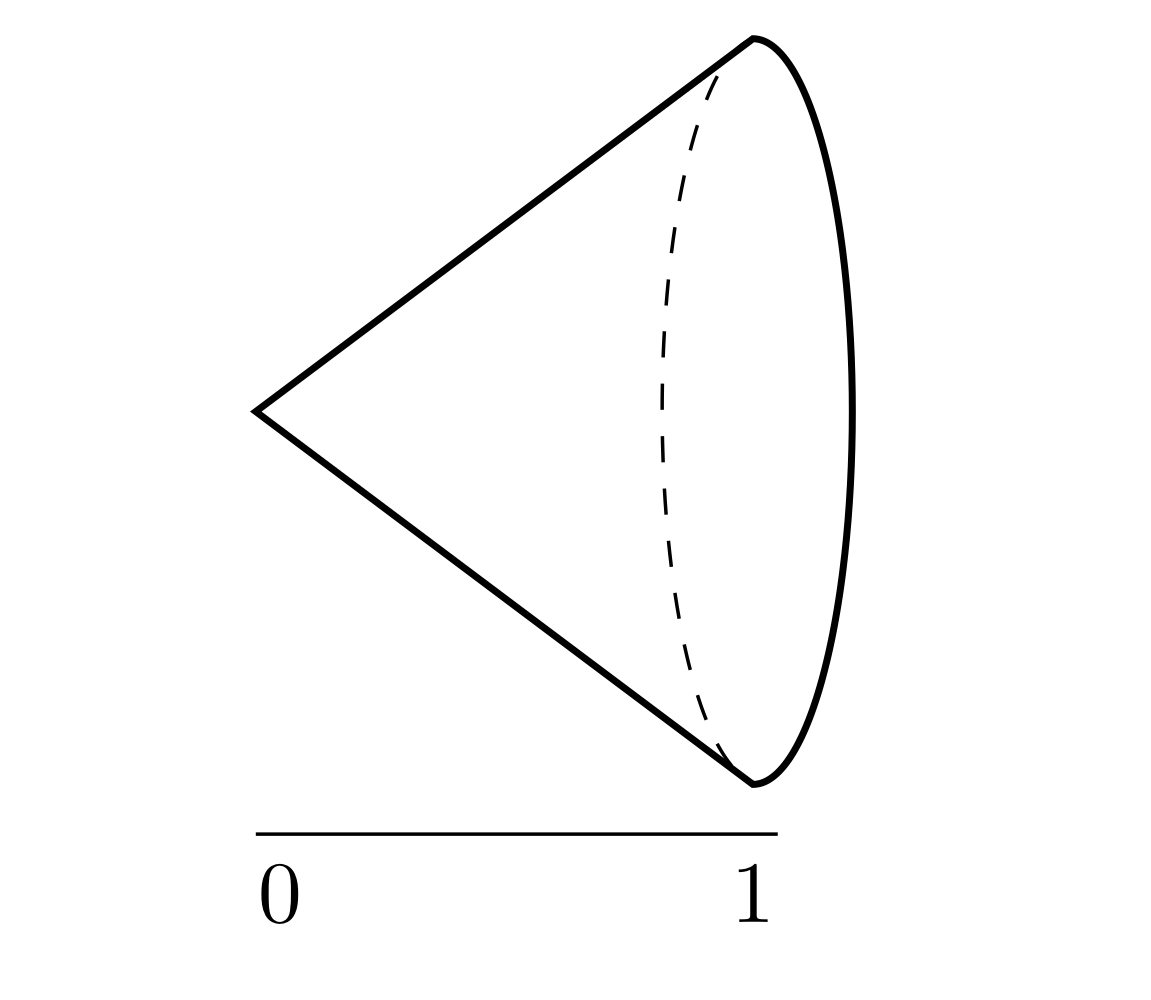
錐

$I = [0, 1] \subset R$ とおく．

$X$ を位相空間とする． $I \times X$ 上の関係
$(0, x) \sim (0, x^{'}), x, x^{'} \in X$
によって生成される同値関係 $R_{c}$ による商空間，すなわち部分集合 ${0} \times X \subset I \times X$ を一点につぶして得られる空間 $(I \times X) / ({0} \times X)$ を $X$ の錐（cone）といい $C X$ で表わす．
錐

錐の閉部分空間

$X$ は $C X$ の閉部分空間
$q_{C X} ({1} \times X) = {[1, x] ∣ x \in X}$
と同相である．以下，この同相により $X \subset C X$ とみなす．

$q_{C X}^{- 1} (q_{C X} ({1} \times X)) = {1} \times X \in τ^{c} (I \times X)$ より， $q_{C X} ({1} \times X) \in τ^{c} (C X)$ である．
${0} \times X \in τ^{c} (I \times X)$ であるから，命題5.7より，
$X \approx {1} \times X \approx q_{C X} ({1} \times X); x \mapsto [1, x]$
が成り立つ．

球面の錐

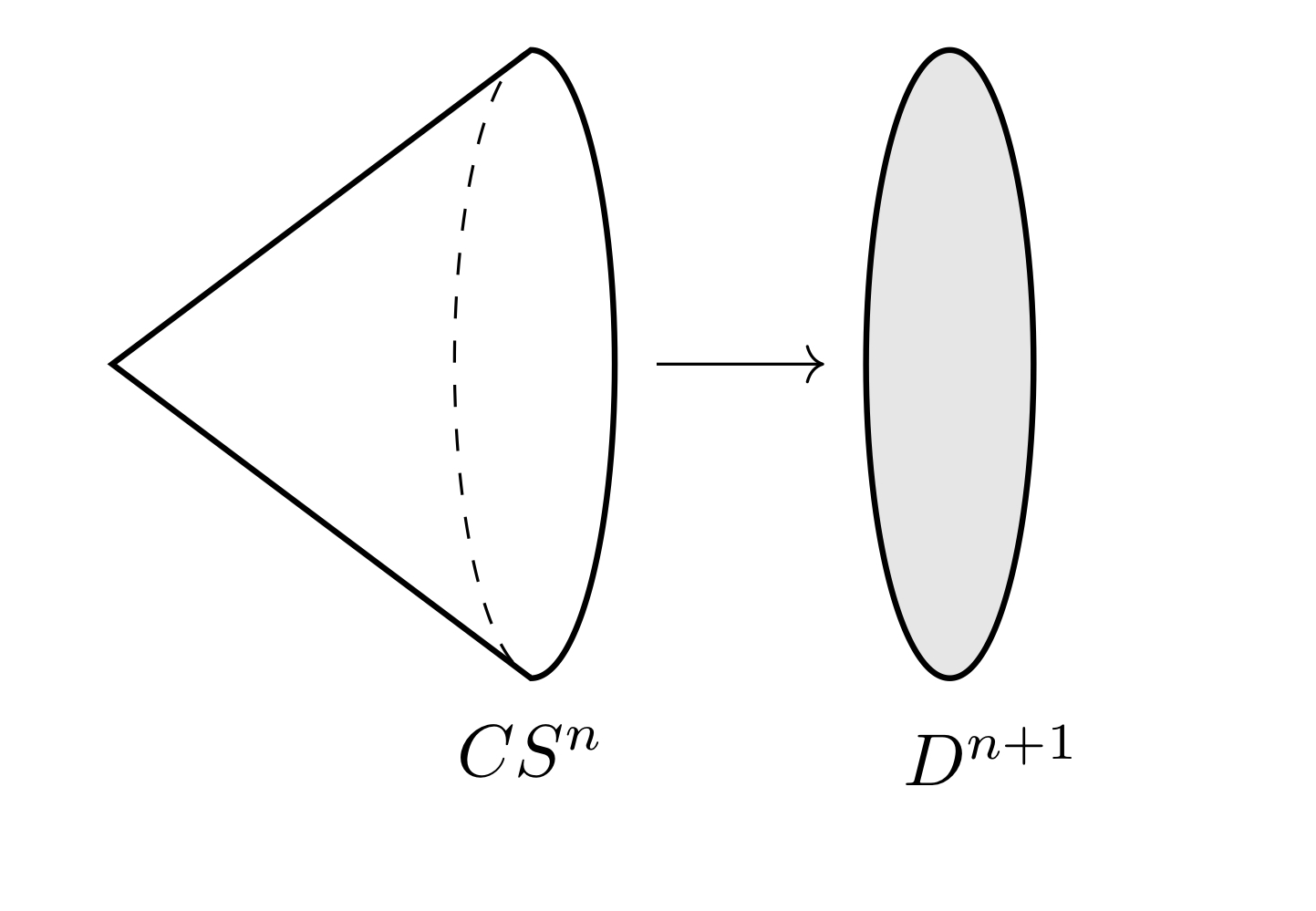
$n$ 次元球面 $S^{n}$ の錐 $C S^{n}$ は $n + 1$ 次元球体 $D^{n + 1}$ に同相である．実際，連続写像
$I \times S^{n} \to D^{n + 1}; (t, x) \mapsto t x$
がコンパクト空間 $C S^{n}$ からハウスドルフ空間 $D^{n + 1}$ への全単射連続写像を誘導する．

閉部分空間の錐

非空閉集合 $A \subset X$ の錐 $C A$ は $C X$ の閉部分空間
$C X | A := {[t, x] \in C X ∣ x \in A}$
と同相である．

$B := q_{C X}^{- 1} (C X | A) = I \times A \cup {0} \times X \in τ^{c} (I \times X)$ より $C X | A \in τ^{c} (C X)$ であるので，命題5.4より同相
$B / (R_{c} | B) \approx C X | A$
が成り立つ．また， $R_{c} | B$ が
$(0, x) \sim (0, x^{'}), x, x^{'} \in X$
によって生成される同値関係に一致することに注意すると以下がわかる：

包含写像 $I \times A \to B$ は連続写像 $C A \to B / (R_{c} | B)$ を誘導する；
$a \in A$ を取る．連続写像 $q_{C A} : I \times A \to C A$ および ${0} \times X \to C A; (0, x) \mapsto [0, a]$ が貼り合わさって定まる連続写像 $B \to C A$ は連続写像 $B / (R_{c} | B) \to C A$ を誘導する；
これらは互いの逆写像である．

命題5.3より次を得る：

連続写像 $f : X \to Y$ は，連続写像
$C f : C X \to C Y; [t, x] \mapsto [t, f (x)]$
を誘導する． $C f$ を $f$ の錐という．

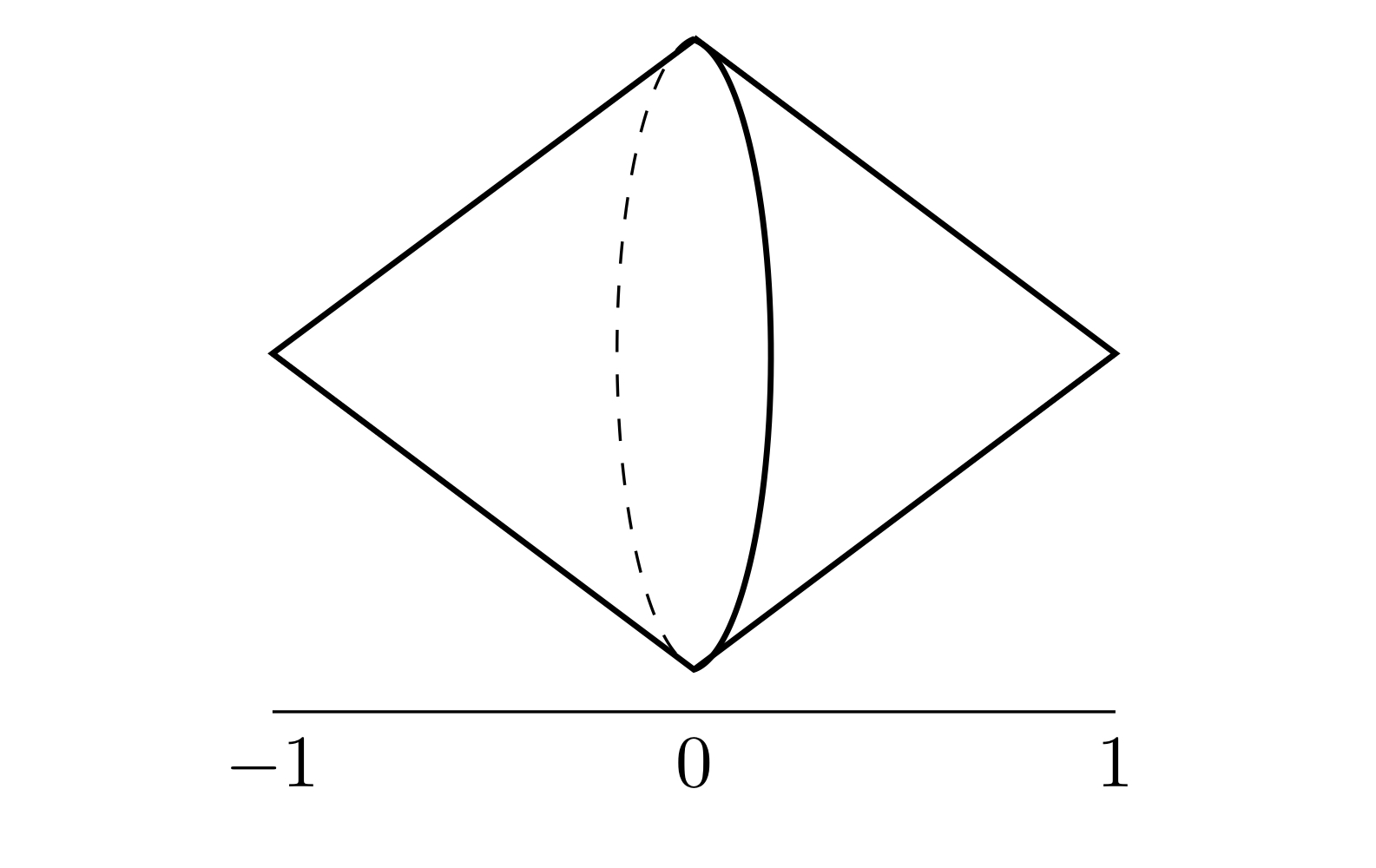
懸垂

$J = [- 1, 1] \subset R$ とおく．

$X$ を位相空間とする． $J \times X$ 上の関係
$(- 1, x) \sim (- 1, x^{'}), (1, x) \sim (1, x^{'}), x, x^{'} \in X$
によって生成される同値関係 $R_{s}$ による商空間を $X$ の懸垂（suspension）といい $S X$ で表わす．
懸垂

懸垂の閉部分空間

位相空間 $X$ の懸垂 $S X$ について次が成り立つ：

$S X$ と $C X / X$ とは同相である；
$C X$ は $S X$ の閉部分空間 $S X_{-} := {[t, x] \in S X ∣ t \leq 0}$ と同相である；
$C X$ は $S X$ の閉部分空間 $S X_{+} := {[t, x] \in S X ∣ t \geq 0}$ と同相である；
$X$ は $S X$ の閉部分空間 $S X_{0} := {[t, x] \in S X ∣ t = 0}$ と同相である；
同相 $S X \approx C X \cup_{X} C X$ が成り立つ．

同相写像
$I \times X \to J \times X; (t, x) \mapsto (2 t - 1, x)$
が同相写像 $C X / X \to S X$ を誘導する（命題5.3）．
$B := q_{S X}^{- 1} (S X_{-}) = [- 1, 0] \times X \in τ^{c} (J \times X)$ より $S X_{-} \in τ^{c} (S X)$ であり， $R_{s} | B$ は
$(- 1, x) \sim (- 1, x^{'}), x, x^{'} \in X$
によって生成される同値関係に一致するので，命題5.4より同相
$C X \approx B / (R_{s} | B) \approx S X_{-}; [t, x] \mapsto [t - 1, x]$
が成り立つ．
(ii)と同様．ただし
$C X \approx S X_{+}; [t, x] \mapsto [1 - t, x]$
となる．
命題1と前段より明らか．
前段と命題5.15よりしたがう．

球面の懸垂

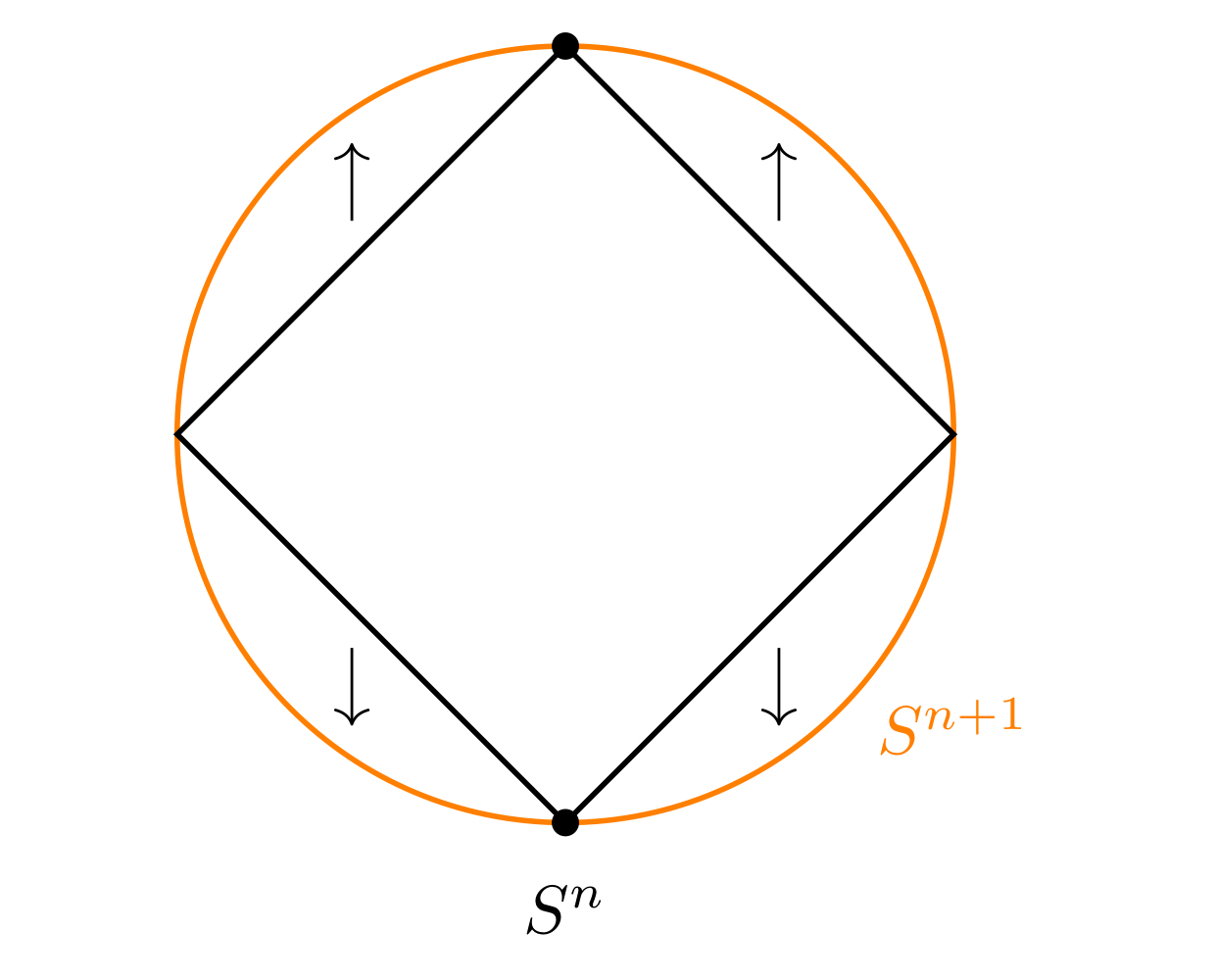
$n$ 次元球面 $S^{n}$ の懸垂 $S S^{n}$ は $n + 1$ 次元球面 $S^{n + 1} \subset R \times R^{n + 1}$ に同相である．実際，連続写像
$J \times S^{n} \to S^{n + 1}; (t, x) \mapsto (t, \sqrt{1 - t^{2}} \cdot x)$
がコンパクト空間 $S S^{n}$ からハウスドルフ空間 $S^{n + 1}$ への全単射連続写像を誘導する．

$n$ 次元球体 $D^{n}$ の境界 $S^{n - 1}$ を一点につぶして得られる空間 $D^{n} / S^{n - 1}$ は $n$ 次元球面 $S^{n}$ に同相である．実際，
$D^{n} / S^{n - 1} \approx C S^{n - 1} / S^{n - 1} \approx S S^{n - 1} \approx S^{n}$
が成り立つ．

閉部分空間の懸垂

非空閉集合 $A \subset X$ の懸垂 $S A$ は $S X$ の閉部分空間
$S X | A := {[t, x] \in S X ∣ x \in A}$
と同相である．

$B := q_{S X}^{- 1} (S X | A) = J \times A \cup {- 1, 1} \times X \in τ^{c} (J \times X)$ より $S X | A \in τ^{c} (S X)$ であり， $R_{s} | B$ は
$(- 1, x) \sim (- 1, x^{'}), (1, x) \sim (1, x^{'}), x, x^{'} \in X$
によって生成される同値関係に一致するので，命題5.4より同相
$S A \approx B / (R_{s} | B) \approx S X | A$
が成り立つ．

連続写像 $f : X \to Y$ は，連続写像
$S f : S X \to S Y; [t, x] \mapsto [t, f (x)]$
を誘導する． $S f$ を $f$ の懸垂という．

結

$X, Y$ を位相空間とする． $X \times I \times Y$ 上の関係
$(x, 0, y) \sim (x, 0, y^{'}), (x, 1, y) \sim (x^{'}, 1, y), x, x^{'} \in X, y, y^{'} \in Y$
によって生成される同値関係 $R_{j}$ による商空間を $X, Y$ の結（join）といい $X * Y$ で表わす．
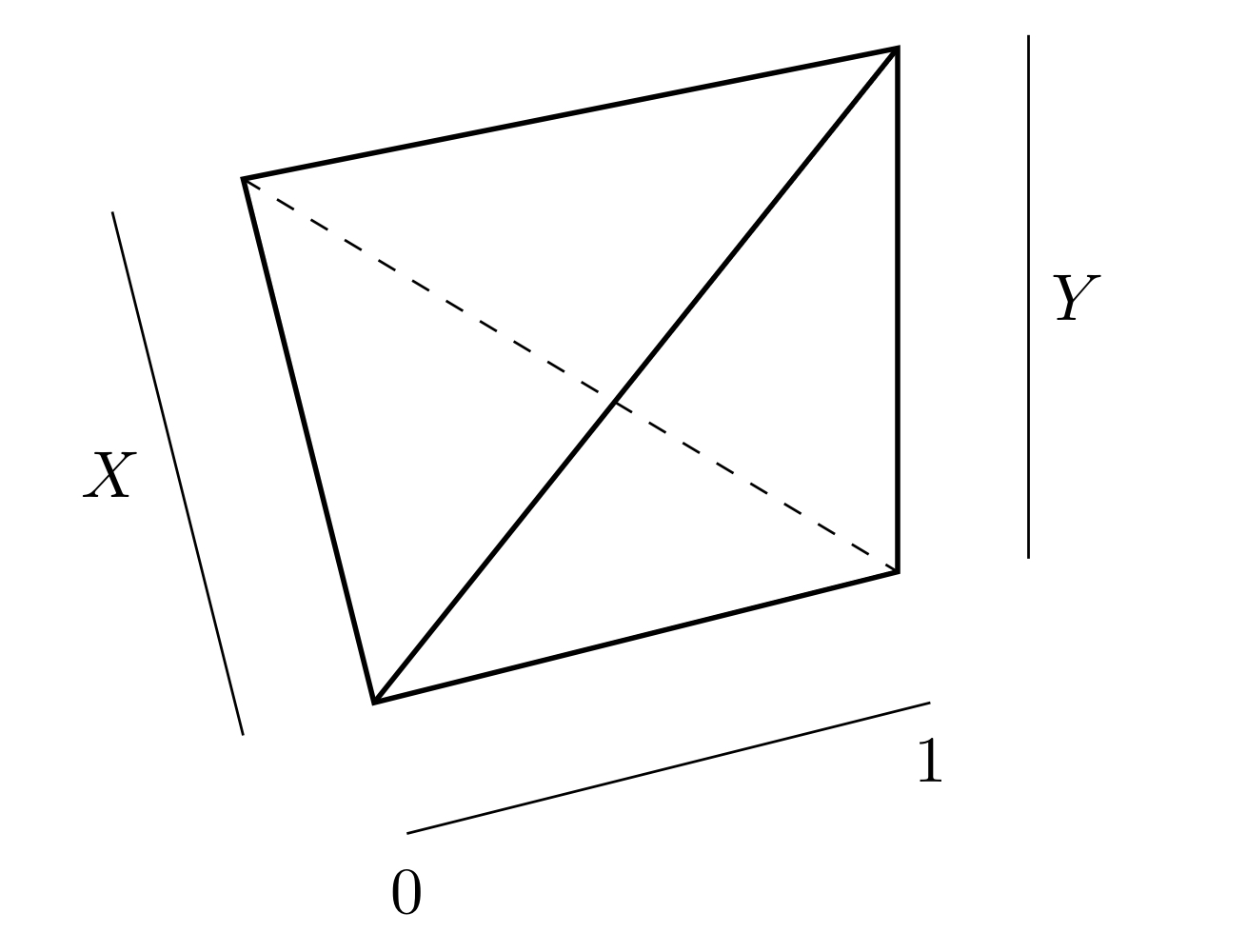結

結の閉部分空間

$X, Y$ を位相空間とする．このとき次が成り立つ：

$X$ は $X * Y$ の閉部分空間
$X *_{0} Y := {[x, t, y] \in X * Y ∣ t = 0}$
と同相である；
$Y$ は $X * Y$ の閉部分空間
$X *_{1} Y := {[x, t, y] \in X * Y ∣ t = 1}$
と同相である；
$X \times Y$ は $X * Y$ の閉部分空間
$X *_{\frac{1}{2}} Y := {[x, t, y] \in X * Y ∣ t = \frac{1}{2}}$
と同相である；
$X * Y$ と $Y * X$ とは同相である．

$B_{0} := q_{X * Y}^{- 1} (X *_{0} Y) = X \times {0} \times Y \in τ^{c} (X \times I \times Y)$ より $X *_{0} Y \in τ^{c} (X * Y)$ であり， $R_{j} | B_{0} = R (p_{X})$ であるから，命題5.4より
$X \approx B_{0} / R (p_{X}) \approx X *_{0} Y; x \mapsto [x, 0, y]$
が成り立つ．ただし $p_{X} : B_{0} \to X$ は自然な射影である．
(i)と同様．
$B_{\frac{1}{2}} := q_{X * Y}^{- 1} (X *_{\frac{1}{2}} Y) = X \times {\frac{1}{2}} \times Y \in τ^{c} (X \times I \times Y)$ より $X *_{\frac{1}{2}} Y \in τ^{c} (X * Y)$ であり， $R_{j} | B_{\frac{1}{2}} = Δ_{B_{\frac{1}{2}}} = R ({id}_{B_{\frac{1}{2}}})$ であるから，命題5.4より
$X \times Y \approx B_{\frac{1}{2}} \approx B_{\frac{1}{2}} / R ({id}_{B_{\frac{1}{2}}}) \approx X *_{\frac{1}{2}} Y; (x, y) \mapsto [x, \frac{1}{2}, y]$
が成り立つ．
同相写像
$X \times I \times Y \to Y \times I \times X; (x, t, y) \mapsto (y, 1 - t, x)$
が同相写像 $X * Y \to Y * X$ を誘導する．

閉部分空間の結

非空閉集合 $A \subset X, B \subset Y$ の結 $A * B$ は $X * Y$ の閉部分空間
$(X | A) * (Y | B) := {[x, t, y] \in X * Y ∣ x \in A, y \in B}$
と同相である．

$Z := q_{X * Y}^{- 1} ((X | A) * (Y | B)) = A \times I \times B \cup A \times {0} \times Y \cup X \times {1} \times B \in τ^{c} (X \times I \times Y)$
より $(X | A) * (Y | B) \in τ^{c} (X * Y)$ であり， $R_{j} | Z$ は
$\begin{aligned} (a, 0, y) \sim (a, 0, y^{'}), & a \in A, y, y^{'} \in Y, \\ (x, 1, b) \sim (x^{'}, 1, b), & x, x^{'} \in X, b \in B \end{aligned}$
によって生成される同値関係に一致するので，命題5.4より同相
$A * B \approx Z / (R_{j} | Z) \approx (X | A) * (Y | B)$
が成り立つ．

結と錐・懸垂

$X$ を位相空間とする．このとき次が成り立つ：

$D^{0} * X \approx C X$ ;
$S^{0} * X \approx S X$ .

同相写像
$D^{0} \times I \times X \to I \times X; (0, t, x) \mapsto (t, x)$
が同相 $D^{0} * X \approx C X$ を誘導する．
連続写像
$S^{0} \times I \times X \to J \times X; (s, t, x) \mapsto {\begin{cases} (t - 1, x) & , s = - 1 \\ (1 - t, x) & , s = 1 \end{cases}$
は連続写像 $f : S^{0} * X \to S X$ を誘導する．また，閉被覆上の連続写像族
$\begin{aligned} [- 1, 0] \times X \to S^{0} * X & ; (t, x) \mapsto [- 1, 1 + t, x], \\ [0, 1] \times X \to S^{0} * X & ; (t, x) \mapsto [1, 1 - t, x] \end{aligned}$
が ${0} \times X$ 上で貼り合わさって定まる連続写像 $J \times X \to S^{0} * X$ は連続写像 $g : S X \to S^{0} * X$ を誘導する．こうして定まる $f, g$ が互いの逆写像であることは容易に確かめられる．

結の結合性について

等化結と誘導結

$Δ^{n - 1} = {(t_{1}, \dots, t_{n}) \in R^{n} ∣ t_{i} \geq 0, \sum t_{i} = 1} \subset R^{n}$ とおく．

$X_{1}, \dots, X_{n}$ を位相空間とする． $X_{1} \times \dots \times X_{n} \times Δ^{n - 1}$ 上の関係
$(x_{1}, \dots, x_{i - 1}, x_{i}, x_{i + 1}, \dots, x_{n}, (t_{1}, \dots, t_{i - 1}, 0, t_{i + 1}, \dots, t_{n})) \sim (x_{1}, \dots, x_{i - 1}, x_{i}^{'}, x_{i + 1}, \dots, x_{n}, (t_{1}, \dots, t_{i - 1}, 0, t_{i + 1}, \dots, t_{n})), x_{j} \in X_{j}, (t_{1}, \dots, t_{n}) \in Δ^{n - 1}$
で生成される同値関係による商空間を $X_{1}, \dots, X_{n}$ の等化結といい， $X_{1} * \dots * X_{n}$ で表わす．また， $(x_{1}, \dots, x_{n}, (t_{1}, \dots, t_{n}))$ の同値類を $t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n}$ と書く．

同相 $I \to Δ^{1}; t \mapsto (1 - t, t)$ により，位相空間 $X, Y$ の結（定義3）と等化結とは同相である．

等化位相の普遍性より，各 $i \in [n]$ に対して写像
$T_{X_{i}} = T_{i} : X_{1} * \dots * X_{n} \to I; t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n} \mapsto t_{i}$
は連続である．したがって $T_{i}^{- 1} (] 0, 1]) \subset X_{1} * \dots * X_{n}$ は開集合であるから， $(q_{X_{1} * \dots * X_{n}})^{T_{i}^{- 1} (] 0, 1])}$ は等化写像である（命題3.9）．よって，各 $i \in [n]$ に対して写像
$ξ_{X_{i}} = ξ_{i} : T_{i}^{- 1} (] 0, 1]) \to X_{i}; t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n} \mapsto x_{i}$
は連続である．

$X_{1}, \dots, X_{n}$ を位相空間とする．商集合 $X_{1} * \dots * X_{n}$ に写像族 $(T_{1}, \dots, T_{n}, ξ_{1}, \dots, ξ_{n})$ による誘導位相を与えた空間を $X_{1}, \dots, X_{n}$ の誘導結といい， $X_{1} \circ \dots \circ X_{n}$ で表わす．誘導結の元も同様に $t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n}$ と書く．

「等化結」および「誘導結」は（おそらく）本稿のみの用語である．
位相の定め方より恒等写像
$id : X_{1} * \dots * X_{n} \to X_{1} \circ \dots \circ X_{n}$
は連続である．

誘導結の結合性

位相空間 $X_{1}, \dots, X_{n}$ の誘導結について，次が成り立つ：
$(X_{1} \circ \dots \circ X_{m}) \circ (X_{m + 1} \circ \dots \circ X_{n}) \approx X_{1} \circ \dots \circ X_{n}, 1 \leq m < n .$

$X^{'} = X_{1} \circ \dots \circ X_{m}, X^{″} = X_{m + 1} \circ \dots \circ X_{n}$ とおく．

連続写像 $f : X^{'} \circ X^{″} \to X_{1} \circ \dots \circ X_{n}$ の構成

写像 $f : X^{'} \circ X^{″} \to X_{1} \circ \dots \circ X_{n}$ を次で定める：
$x = r (t_{1} x_{1} \oplus \dots \oplus t_{m} x_{m}) \oplus s (t_{m + 1} x_{m + 1} \oplus \dots \oplus t_{n} x_{n}) \mapsto r t_{1} x_{1} \oplus \dots \oplus r t_{m} x_{m} \oplus s t_{m + 1} x_{m + 1} \oplus \dots \oplus s t_{n} x_{n} .$

各 $i \in [n]$ に対して
$f^{- 1} (T_{i}^{- 1} (] 0, 1])) = {\begin{cases} T_{X^{'}}^{- 1} (] 0, 1]) \cap (T_{X_{i}} \circ ξ_{X^{'}})^{- 1} (] 0, 1]) = (T_{X_{i}} \circ ξ_{X^{'}})^{- 1} (] 0, 1]) & , 1 \leq i \leq m \\ T_{X^{″}}^{- 1} (] 0, 1]) \cap (T_{X_{i}} \circ ξ_{X^{″}})^{- 1} (] 0, 1]) = (T_{X_{i}} \circ ξ_{X^{″}})^{- 1} (] 0, 1]) & , m < i \leq n \end{cases} \in τ (X^{'} \circ X^{″})$
が成り立つ．
$i \in [m]$ とする．
- $T_{X^{'}}^{- 1} (] 0, 1])$ 上で，
  $T_{i} \circ f (x) = r t_{i} = T_{X^{'}} (x) \cdot T_{X_{i}} \circ ξ_{X^{'}} (x)$
  より， $T_{i} \circ f$ は連続である．
- 任意の $x := 0 x^{'} \oplus 1 x^{″} \in X^{'} \circ X^{″}$ と $ε > 0$ に対して， $U := T_{X^{'}}^{- 1} ([0, ε [) \in τ (x, X^{'} \circ X^{″})$ であり $T_{i} \circ f (U) \subset [0, ε [$ が成り立つ．したがって $T_{X^{'}}^{- 1} ([0, 1 [)$ 上でも $T_{i} \circ f$ は連続である．
- よって $T_{i} \circ f : X^{'} \circ X^{″} \to I$ は連続である．
- また， $f^{- 1} (T_{i}^{- 1} (] 0, 1]))$ 上で
  $ξ_{i} \circ f (x) = x_{i} = ξ_{X_{i}} \circ ξ_{X^{'}} (x)$
  が成り立つので， $ξ_{i} \circ f^{T_{i}^{- 1} (] 0, 1])}$ は連続である．
同様にして $i \in {m + 1, \dots, n}$ に対しても， $T_{i} \circ f$ および $ξ_{i} \circ f^{T_{i}^{- 1} (] 0, 1])}$ は連続であることがわかる．

よって $f : X^{'} \circ X^{″} \to X_{1} \circ \dots \circ X_{n}$ は連続である（命題2.18）．

連続写像 $g : X_{1} \circ \dots \circ X_{n} \to X^{'} \circ X^{″}$ の構成

写像 $g : X_{1} \circ \dots \circ X_{n} \to X^{'} \circ X^{″}$ を次で定める：
$x = t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n} \mapsto r (t_{1}^{'} x_{1} \oplus \dots \oplus t_{m}^{'} x_{m}) \oplus s (t_{m + 1}^{″} x_{m + 1} \oplus \dots \oplus t_{n}^{″} x_{n}) .$
ただし，
$\begin{aligned} r & = t_{1} + \dots + t_{m}, \\ t_{i}^{'} & = {\begin{cases} \frac{t_{i}}{r} & , r \neq 0 \\ \frac{1}{m} & , r = 0 \end{cases} \\ s & = t_{m + 1} + \dots + t_{n}, \\ t_{i}^{″} & = {\begin{cases} \frac{t_{i}}{s} & , s \neq 0 \\ \frac{1}{n - m} & , s = 0 \end{cases} \end{aligned}$
とおいた．このとき，
$\begin{aligned} T_{X^{'}} \circ g (x) & = r = T_{1} (x) + \dots + T_{m} (x), \\ T_{X^{″}} \circ g (x) & = s = T_{m + 1} (x) + \dots + T_{n} (x) \end{aligned}$
より， $T_{X^{'}} \circ g, T_{X^{″}} \circ g$ は連続である．

$i \in [m]$ とする．このとき，
$\begin{aligned} T_{X_{i}} \circ (ξ_{X^{'}} \circ g^{T_{X^{'}}^{- 1} (] 0, 1])}) (x) & = T_{X_{i}} (\frac{t_{1}}{r} x_{1} \oplus \dots \oplus \frac{t_{m}}{r} x_{m}) \\ = \frac{t_{i}}{r} \\ = \frac{T_{i} (x)}{T_{1} (x) + \dots + T_{m} (x)} \end{aligned}$
および
$\begin{aligned} ξ_{X_{i}} \circ (ξ_{X^{'}} \circ g^{T_{X^{'}}^{- 1} (] 0, 1])})^{T_{X_{i}}^{- 1} (] 0, 1])} (x) & = ξ_{X_{i}} (\frac{t_{1}}{r} x_{1} \oplus \dots \oplus \frac{t_{m}}{r} x_{m}) \\ = x_{i} \\ = ξ_{i} (x) \end{aligned}$
が成り立つ．したがって $ξ_{X^{'}} \circ g^{T_{X^{'}}^{- 1} (] 0, 1])}$ は連続である（命題2.18）．
同様にして $ξ_{X^{″}} \circ g^{T_{X^{″}}^{- 1} (] 0, 1])}$ の連続性もわかる．

よって $g : X_{1} \circ \dots X_{n} \to X^{'} \circ X^{″}$ は連続である．

$f, g$ が互いの逆写像であること

$\begin{aligned} g \circ f (r (t_{1} x_{1} \oplus \dots \oplus t_{m} x_{m}) \oplus s (t_{m + 1} x_{m + 1} \oplus \dots \oplus t_{n} x_{n})) & = g (r t_{1} x_{1} \oplus \dots \oplus r t_{m} x_{m} \oplus s t_{m + 1} x_{m + 1} \oplus \dots \oplus s t_{n} x_{n}) \\ = {\begin{cases} r (t_{1} x_{1} \oplus \dots \oplus t_{m} x_{m}) \oplus s (t_{m + 1} x_{m + 1} \oplus \dots \oplus t_{n} x_{n}) & , r, s \neq 0 \\ 0 (\frac{1}{m} x_{1} \oplus \dots \oplus \frac{1}{m} x_{m}) \oplus 1 (t_{m + 1} x_{m + 1} \oplus \dots \oplus t_{n} x_{n}) & , r = 0 \\ 1 (t_{1} x_{1} \oplus \dots \oplus t_{m} x_{m}) \oplus 0 (\frac{1}{n - m} x_{m + 1} \oplus \dots \oplus \frac{1}{n - m} x_{n}) & , s = 0 \end{cases} \\ = r (t_{1} x_{1} \oplus \dots \oplus t_{m} x_{m}) \oplus s (t_{m + 1} x_{m + 1} \oplus \dots \oplus t_{n} x_{n}) \end{aligned}$
および
$\begin{aligned} f \circ g (t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n}) & = f (r (t_{1}^{'} x_{1} \oplus \dots \oplus t_{m}^{'} x_{m}) \oplus s (t_{m + 1}^{″} x_{m + 1} \oplus \dots \oplus t_{n}^{″} x_{n})) \\ = r t_{1}^{'} x_{1} \oplus \dots \oplus r t_{m}^{'} x_{m} \oplus s t_{m + 1}^{″} x_{m + 1} \oplus \dots \oplus s t_{n}^{″} x_{n} \\ = t_{1} x_{1} \oplus \dots \oplus t_{n} x_{n} \end{aligned}$
が成り立つ．

命題10の

位相空間 $X_{1}, X_{2}, X_{3}$ の誘導結について
$X_{1} \circ (X_{2} \circ X_{3}) \approx (X_{1} \circ X_{2}) \circ X_{3}$
が成り立つ．

等化結の結合性：コンパクトハウスドルフ空間の場合

誘導結のハウスドルフ性

$X_{1}, X_{2}$ がハウスドルフ空間ならば，誘導結 $X_{1} \circ X_{2}$ もハウスドルフ空間である．

$x := t_{1} x_{1} \oplus t_{2} x_{2} \neq t_{1}^{'} x_{1}^{'} \oplus t_{2}^{'} x_{2}^{'} =: x^{'}$ とする．このとき，“ $x_{1}$ と $x_{2}$ とを結ぶ線分”と，“ $x_{1}^{'}$ と $x_{2}^{'}$ とを結ぶ線分”との位置関係（cf. 図5）に注意すると，

$t_{1} \neq t_{1}^{'}$ ;
$t_{2} \neq t_{2}^{'}$ ;
$t_{1} = t_{1}^{'} \neq 0 \land x_{1} \neq x_{1}^{'}$ ;
$t_{2} = t_{2}^{'} \neq 0 \land x_{2} \neq x_{2}^{'}$

のうち少なくとも一つが成り立つことがわかる．したがって，写像

$T_{1} : X_{1} \circ X_{2} \to I; s_{1} y_{1} \oplus s_{2} y_{2} \mapsto s_{1}$ ;
$T_{2} : X_{1} \circ X_{2} \to I; s_{1} y_{1} \oplus s_{2} y_{2} \mapsto s_{2}$ ;
$ξ_{1} : T_{1}^{- 1} (] 0, 1]) \to X_{1}; s_{1} y_{1} \oplus s_{2} y_{2} \mapsto y_{1}$ ;
$ξ_{2} : T_{2}^{- 1} (] 0, 1]) \to X_{2}; s_{1} y_{1} \oplus s_{2} y_{2} \mapsto y_{2}$

の連続性および $I, X_{1}, X_{2}$ のハウスドルフ性より， $x, x^{'}$ は交わらない開近傍を持つ（補題2.22）．

$X_{1}, \dots, X_{n}$ をコンパクトハウスドルフ空間とする．このとき恒等写像
$id : X_{1} * \dots * X_{n} \to X_{1} \circ \dots \circ X_{n}$
は同相写像である．

$X_{1}, \dots, X_{n}, Δ^{n - 1}$ はコンパクト空間なので， $X_{1} * \dots * X_{n}$ はコンパクト空間である．
命題10，補題11より，
$X_{1} \circ \dots \circ X_{n} \approx (\dots ((X_{1} \circ X_{2}) \circ X_{3}) \dots) \circ X_{n}$
はハウスドルフ空間である．

命題12の証明より次がわかる： $X_{1}, \dots, X_{n}$ がハウスドルフ空間ならば，誘導結 $X_{1} \circ \dots \circ X_{n}$ および等化結 $X_{1} * \dots * X_{n}$ はハウスドルフ空間である．

命題12の

コンパクトハウスドルフ空間 $X_{1}, X_{2}, X_{3}$ の等化結について
$X_{1} * (X_{2} * X_{3}) \approx (X_{1} * X_{2}) * X_{3}$
が成り立つ．

命題10（の系）と命題12より
$\begin{aligned} X_{1} * (X_{2} * X_{3}) & \approx X_{1} * (X_{2} \circ X_{3}) \\ \approx X_{1} \circ (X_{2} \circ X_{3}) \\ \approx (X_{1} \circ X_{2}) \circ X_{3} \\ \approx (X_{1} * X_{2}) \circ X_{3} \\ \approx (X_{1} * X_{2}) * X_{3} \end{aligned}$
を得る．

錐と懸垂の可換性

コンパクトハウスドルフ空間 $X$ に対して，同相
$C S X \approx S C X$
が成り立つ．実際， $D^{0}, S^{0}$ はコンパクトハウスドルフ空間であるから，命題9，命題7(iv)より
$C S X \approx D^{0} * (S^{0} * X) \approx (D^{0} * S^{0}) * X \approx (S^{0} * D^{0}) * X \approx S^{0} * (D^{0} * X) \approx S C X$
を得る．

球面の等化結

非負整数 $m, n \in Z_{\geq 0}$ に対して，同相
$S^{m} * S^{n} \approx S^{m + n + 1}$
が成り立つ．

$m \in Z_{\geq 0}$ に関する数学的帰納法による．

$m = 0$ のとき，命題9，例2より
$S^{0} * S^{n} \approx S S^{n} \approx S^{n + 1} = S^{0 + n + 1}$
が成り立つ．
$m > 0$ のとき，
$\begin{aligned} S^{m} * S^{n} & \approx (S S^{m - 1}) * S^{n} \\ \approx (S^{0} * S^{m - 1}) * S^{n} \\ \approx S^{0} * (S^{m - 1} * S^{n}) \\ \approx S^{0} * S^{(m - 1) + n + 1} = S^{0} * S^{m + n} \\ \approx S S^{m + n} \\ \approx S^{m + n + 1} \end{aligned}$
が成り立つ．

等化結の結合性：局所コンパクトハウスドルフ空間の場合（未）

あやしくなってきた．

基点つき空間

位相空間 $X$ とその点 $x_{0} \in X$ の組 $(X, x_{0})$ を基点つき空間（pointed space）という．
$(X, x_{0}), (Y, y_{0})$ を基点つき空間とする．連続写像 $f : X \to Y$ が $f (x_{0}) = y_{0}$ を満たすとき， $f$ を基点つき空間のあいだの連続写像といい $f : (X, x_{0}) \to (Y, y_{0})$ と書く．

以下，基点つき空間 $(X, x_{0})$ に対しては ${x_{0}} \in τ^{c} (X)$ を仮定する．

被約錐・被約懸垂

$(X, x_{0})$ を基点つき空間とする．

$I \times X$ の部分集合 $I \times {x_{0}} \cup {0} \times X$ を一点につぶして得られる空間を $X$ の被約錐（reduced cone）といい， $\hat{C} X$ で表わす．被約錐は $q_{\hat{C} X} (0, x_{0})$ を基点とする基点つき空間とみなす．
$J \times X$ の部分集合 $J \times {x_{0}} \cup {- 1, 1} \times X$ を一点につぶして得られる空間を $X$ の被約懸垂（reduced suspension）といい， $Σ X$ で表わす．被約懸垂は $q_{Σ X} (- 1, x_{0})$ を基点とする基点つき空間とみなす．

$(X, x_{0})$ を基点つき空間とする．このとき次が成り立つ：

被約錐 $\hat{C} X$ は $C X / C {x_{0}}$ に同相である；
被約懸垂 $Σ X$ は $S X / S {x_{0}}$ に同相である；
$X$ は閉部分空間 $q_{\hat{C} X} ({1} \times X) \subset \hat{C} X$ に同相である；
$Σ X$ は $\hat{C} X / X$ に同相である；
$\hat{C} X$ は閉部分空間 $Σ X_{\pm} := {[t, x] \in Σ X ∣ \pm t \geq 0}$ に同相である；
$X$ は閉部分空間 $Σ X_{0} := {[t, x] \in Σ X ∣ t = 0}$ に同相である；
同相 $Σ X \approx \hat{C} X \cup_{X} \hat{C} X$ が成り立つ．

${x_{0}} \in τ^{c} (X)$ より $C {x_{0}} \approx q_{C X} (I \times {x_{0}})$ が成り立つ（命題2）．いま $(0, x_{0}) \in I \times {x_{0}} \cap {0} \times X \neq \emptyset$ であるから，命題5.5より
$\begin{aligned} C X / C {x_{0}} & \approx ((I \times X) / ({0} \times X)) / q_{I \times X / {0} \times X} (I \times {x_{0}}) \\ \approx (I \times X) / (I \times {x_{0}} \cup {0} \times X) \\ = \hat{C} X \end{aligned}$
が成り立つ．
${x_{0}} \in τ^{c} (X)$ より $S {x_{0}} \approx q_{S X} (J \times {x_{0}})$ が成り立つ（命題5）．よって，命題4，命題5.5より
$\begin{aligned} S X / S {x_{0}} & \approx (C X / X) / q_{C X / X} (q_{C X} (I \times {x_{0}})) \\ \approx C X / q_{C X} (I \times {x_{0}} \cup {1} \times X) \\ = ((I \times X) / ({0} \times X)) / q_{I \times X / {0} \times X} (I \times {x_{0}} \cup {1} \times X) \\ \approx (I \times X) / (I \times {x_{0}} \cup {0, 1} \times X) \\ \approx (J \times X) / (J \times {x_{0}} \cup {- 1, 1} \times X) \\ = Σ X \end{aligned}$
が成り立つ．
$B := q_{\hat{C} X}^{- 1} (q_{\hat{C} X} ({1} \times X)) = I \times {x_{0}} \cup {1} \times X \in τ^{c} (I \times X)$ より $q_{\hat{C} X} ({1} \times X) \in τ^{c} (\hat{C} X)$ である．また， $R (I \times {x_{0}} \cup {0} \times X) | B = R (I \times {x_{0}})$ であるから，命題5.4より
$X \approx {1} \times X \approx B / (I \times {x_{0}}) \approx q_{\hat{C} X} ({1} \times X)$
が成り立つ．
前段より
$\begin{aligned} Σ X & \approx (I \times X) / (I \times {x_{0}} \cup {0, 1} \times X) \\ \approx ((I \times X) / (I \times {x_{0}} \cup {0} \times X)) / q_{I \times X / (I \times {x_{0}} \cup {0} \times X)} ({1} \times X) \\ = \hat{C} X / q_{\hat{C} X} ({1} \times X) \\ \approx \hat{C} X / X \end{aligned}$
を得る．
$B := q_{Σ X}^{- 1} (Σ X_{-}) = J \times {x_{0}} \cup [- 1, 0] \times X \in τ^{c} (J \times X)$ より $Σ X_{-} \in τ^{c} (Σ X)$ である．また， $R (J \times {x_{0}} \cup {- 1, 1} \times X) | B$ は $J \times {x_{0}} \cup {- 1} \times X$ を一点につぶす同値関係であるから，連続写像 $I \times X \to B; (t, x) \mapsto (t - 1, x)$ は連続写像 $\hat{C} X \to Σ X_{-}$ を誘導する．また，連続写像
$\begin{aligned} J \times {x_{0}} \to \hat{C} X & ; (t, x_{0}) \mapsto [0, x_{0}] \\ [- 1, 0] \times X \to \hat{C} X & ; (t, x) \mapsto [t + 1, x] \end{aligned}$
が貼り合わさって定まる連続写像 $B \to \hat{C} X$ が逆写像を誘導する． $Σ X_{+}$ についても同様である：
$\hat{C} X \approx Σ X_{+}; [t, x] \mapsto [1 - t, x] .$
前段より
$X \approx q_{\hat{C} X} ({1} \times X) \approx Σ X_{0} \in τ^{c} (Σ X)$
が成り立つ．
前段と命題5.15よりしたがう．

球面の被約錐

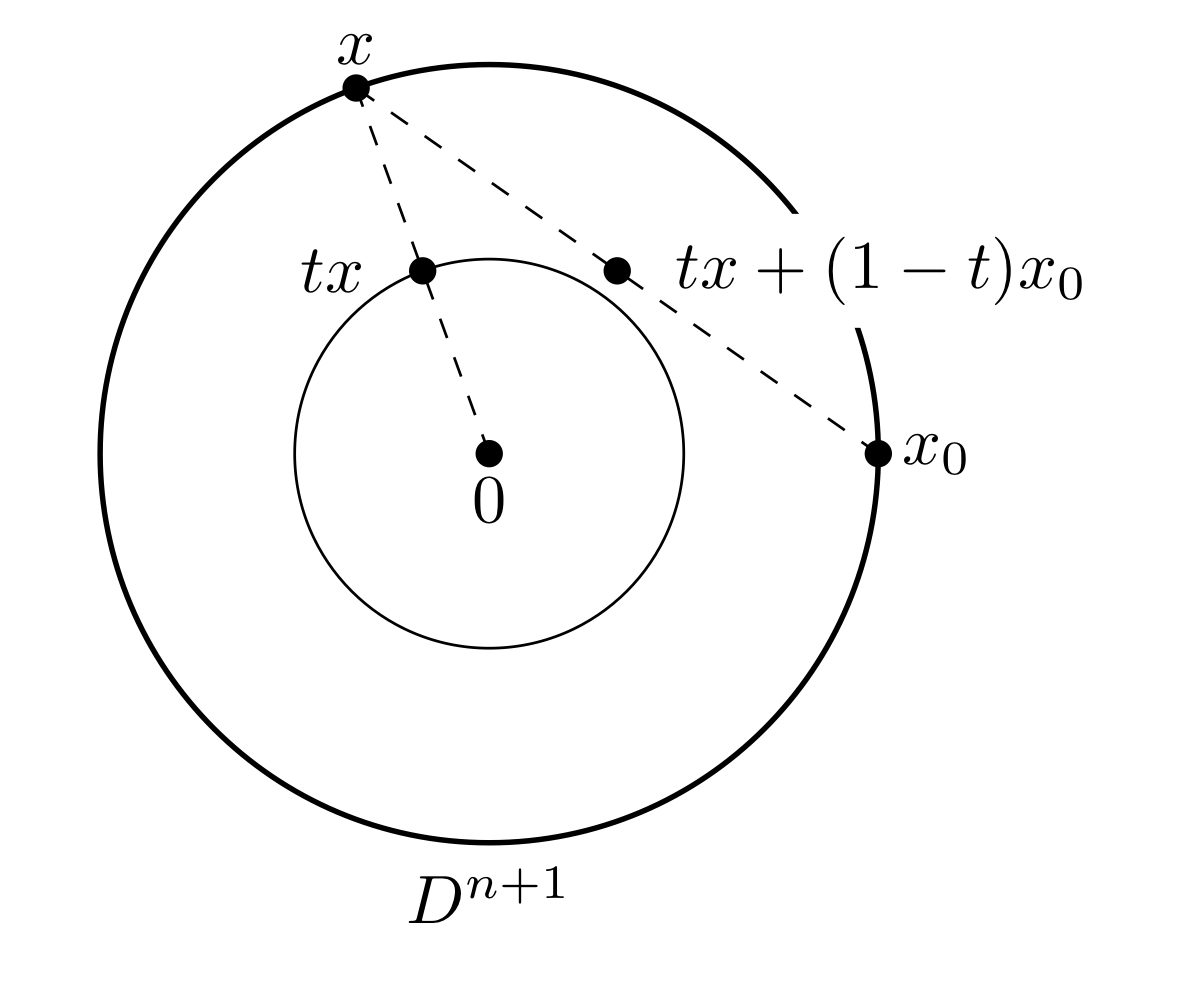
$n$ 次元球面 $S^{n}$ の被約錐 $\hat{C} S^{n}$ は $n + 1$ 次元球体 $D^{n + 1}$ に同相である．実際， $S^{n}$ の基点を $x_{0} \in S^{n}$ とすると，連続写像
$C S^{n} \to D^{n + 1}; [t, x] \mapsto t x + (1 - t) x_{0}$
はコンパクト空間 $\hat{C} S^{n} \approx C S^{n} / C {x_{0}}$ からハウスドルフ空間 $D^{n + 1}$ への全単射連続写像を誘導する．
!FORMULA[325][1004258240][0]をつぶす $C {x_{0}}$ をつぶす

球面の被約懸垂

$n$ 次元球面 $S^{n}$ の被約懸垂 $Σ S^{n}$ は $n + 1$ 次元球面 $S^{n + 1} \subset R \times R^{n + 1}$ に同相である．

$S^{n}$ の基点を $x_{0} \in S^{n}$ とする．写像 $f : S S^{n} \to S^{n + 1}$ を
$f ([t, x]) = {\begin{cases} (\sqrt{1 - ∥ (1 - t) x + t x_{0} ∥^{2}}, (1 - t) x + t x_{0}) & , t \geq 0 \\ (- \sqrt{1 - ∥ (1 + t) x - t x_{0} ∥^{2}}, (1 + t) x - t x_{0}) & , t \leq 0 \end{cases}$
で定める． $f \circ q_{S S^{n}}$ が連続なので $f$ は連続である．連続写像 $f$ は， $S S_{\pm}^{n} \approx C S^{n}$ （命題4）を例6の写像により $D^{n + 1} \approx {0} \times D^{n + 1} \subset R \times R^{n + 1}$ に押しつけたものを同相写像
$D^{n + 1} \to S^{n + 1} \cap ({x \in R ∣ \pm x \geq 0} \times R^{n + 1}); z \mapsto (\pm \sqrt{1 - ∥ z ∥^{2}}, z)$
で“左右に膨らませる”写像である．したがって， $f$ はコンパクト空間 $Σ S^{n} \approx S S^{n} / S {x_{0}}$ からハウスドルフ空間 $S^{n + 1}$ への全単射連続写像を誘導する．
!FORMULA[344][-1977159728][0]をつぶす $S {x_{0}}$ をつぶす

命題13，例6，例1より
$Σ S^{n} \approx \hat{C} S^{n} / S^{n} \approx D^{n + 1} / S^{n} \approx S^{n + 1}$
を得る．

被約錐と被約懸垂の可換性

基点つき空間 $(X, x_{0})$ に対して，同相
$\hat{C} Σ X \approx Σ \hat{C} X$
が成り立つ．

単位閉区間 $I = [0, 1]$ はコンパクトハウスドルフ空間なので
${id}_{I} \times q_{Σ X} : I \times J \times X \to I \times Σ X$
は全射等化写像である（定理4.11の系）．したがって，合成
$q := q_{\hat{C} Σ X} \circ ({id}_{I} \times q_{Σ X}) : I \times J \times X \to \hat{C} Σ X$
は全射等化写像である（定理3.7の系）．また，同値関係 $R (q)$ は部分集合
$(I \times J \times {x_{0}}) \cup ({0} \times J \times X) \cup (I \times {- 1, 1} \times X)$
を一点につぶす同値関係である．同様に
$q^{'} := q_{Σ \hat{C} X} \circ ({id}_{J} \times q_{\hat{C} X}) : J \times I \times X \to Σ \hat{C} X$
は全射等化写像であり，
$R (q^{'}) = R ((J \times I \times {x_{0}}) \cup (J \times {0} \times X) \cup ({- 1, 1} \times I \times X))$
が成り立つ．よって，同相写像
$I \times J \times X \to J \times I \times X; (s, t, x) \mapsto (t, s, x)$
が同相
$\hat{C} Σ X \approx Σ \hat{C} X$
を誘導する．

楔和

$((X_{λ}, x_{λ, 0}))_{λ \in Λ}$ を基点つき空間の族とする．余積空間 $∐ X_{∙}$ 上の関係
$(λ, x_{λ, 0}) \sim (μ, x_{μ, 0}), λ, μ \in Λ$
によって生成される同値関係による商空間，すなわち部分集合 ${(λ, x_{λ, 0}) ∣ λ \in Λ}$ を一点につぶして得られる空間を $((X_{λ}, x_{λ, 0}))_{λ \in Λ}$ の楔和（wedge sum）といい， $⋁ X_{∙}, \underset{λ \in Λ}{⋁} X_{λ}$ などで表わす．楔和は $q_{⋁ X_{∙}} (λ, x_{λ, 0})$ を基点とする基点つき空間とみなす．

余積空間の結合性（resp. 可換性）より，楔和の結合性（resp. 可換性）がしたがう．

楔和の普遍性

$((X_{λ}, x_{λ, 0}))_{λ \in Λ}$ を基点つき空間の族とする．基点つき空間 $(Y, y_{0})$ への連続写像族 $f_{∙} = (f_{λ} : (X_{λ}, x_{λ, 0}) \to (Y, y_{0}))_{λ \in Λ}$ に対して，基点つき空間のあいだの連続写像 $⋁ f_{∙} = \underset{λ \in Λ}{⋁} f_{λ} : ⋁ X_{∙} \to Y$ であって
$\forall λ \in Λ, ⋁ f_{∙} \circ q_{⋁ X_{∙}} \circ i_{λ} = f_{λ}$
が成り立つものがただ一つ存在する．

余積空間の普遍性より連続写像 $\nabla (f_{∙}) : ∐ X_{∙} \to Y$ が定まる：
$X_{λ} f_{λ} i_{λ} Y ∐ X_{∙} \nabla (f_{∙})$
いま
$\forall λ \in Λ, f_{λ} (x_{λ, 0}) = y_{0}$
より，
$q_{⋁ X_{∙}} (x) = q_{⋁ X_{∙}} (y) ⟹ \nabla (f_{∙}) (x) = \nabla (f_{∙}) (y)$
が成り立つ．よって，商空間の普遍性より連続写像 $⋁ f_{∙} : ⋁ X_{∙} \to Y$ が定まる：
$∐ X_{∙} \nabla (f_{∙}) q_{⋁ X_{∙}} Y ⋁ X_{∙} ⋁ f_{∙}$
この $⋁ f_{∙}$ が条件を満たすことは明らかであろう．

楔和のハウスドルフ性

$((X_{λ}, x_{λ, 0}))_{λ \in Λ}$ を基点つきハウスドルフ空間の族とする．このとき，楔和 $⋁ X_{∙}$ はハウスドルフ空間である．

$X = ∐ X_{∙}, q = q_{⋁ X_{∙}}$ とおく．命題3.19より $X$ はハウスドルフ空間である．

$x, y \in X, q (x) \neq q (y),$ とする． $x \neq y$ と $X$ のハウスドルフ性より $x, y \in X$ の交わらない開近傍 $U, V \in τ (X)$ が存在する．また， $X = ⋃_{λ \in Λ} i_{λ} (X_{λ})$ より， $λ, μ \in Λ$ であって $x \in i_{λ} (X_{λ}), y \in i_{μ} (X_{μ})$ となるものが存在する．

$x \in i_{λ} (X_{λ} ∖ {x_{λ, 0}}), y = i_{μ} (x_{μ, 0})$ のとき

$x \neq i_{λ} (x_{λ, 0})$ より，それぞれの交わらない開近傍 $U_{0}, V_{0} \in τ (X)$ が存在する．そこで $U^{'} = U \cap U_{0} \cap i_{λ} (X_{λ} ∖ {x_{λ, 0}}), V^{'} = V \cup V_{0} \cup ⋃_{λ^{'} \neq λ} i_{λ^{'}} (X_{λ^{'}})$ とおくと，
$q^{- 1} (q (U^{'})) = U^{'} \in τ (x, X), q^{- 1} (q (V^{'})) = V^{'} \in τ (y, X), U^{'} \cap V^{'} = \emptyset$
より，
$q (U^{'}) \in τ (q (x), ⋁ X_{∙}), q (V^{'}) \in τ (q (y), ⋁ X_{∙}), q (U^{'}) \cap q (V^{'}) = \emptyset$
が成り立つ．

$x \in i_{λ} (X_{λ} ∖ {x_{λ, 0}}), y \in i_{μ} (X_{μ} ∖ {x_{μ, 0}})$ のとき

$U^{'} = U \cap i_{λ} (X_{λ} ∖ {x_{λ, 0}}), V^{'} = V \cap i_{μ} (X_{μ} ∖ {x_{μ, 0}})$ とおくと，
$q^{- 1} (q (U^{'})) = U^{'} \in τ (x, X), q^{- 1} (q (V^{'})) = V^{'} \in τ (y, X), U^{'} \cap V^{'} = \emptyset$
より，
$q (U^{'}) \in τ (q (x), ⋁ X_{∙}), q (V^{'}) \in τ (q (y), ⋁ X_{∙}), q (U^{'}) \cap q (V^{'}) = \emptyset$
が成り立つ．

$(X_{1}, x_{1, 0}), \dots, (X_{n}, x_{n, 0})$ を基点つき空間とする．このとき
$X_{1} \lor \dots \lor X_{n} = ⋃_{i \in [n]} {x_{1, 0}} \times \dots \times {x_{i - 1, 0}} \times X_{i} \times {x_{i + 1, 0}} \times \dots \times {x_{n, 0}} \subset X_{1} \times \dots \times X_{n}$
とおくと，これは $(x_{1, 0}, \dots, x_{n, 0})$ を基点とする基点つき空間であり，楔和 $\underset{i \in [n]}{⋁} X_{i}$ と同相である．

商写像を $q : ∐ X_{∙} \to ⋁ X_{∙}$ とおく．

各 $i \in [n]$ に対して
$X_{i}^{'} = {x_{1, 0}} \times \dots \times {x_{i - 1, 0}} \times X_{i} \times {x_{i + 1, 0}} \times \dots \times {x_{n, 0}}$
とおくと，これは $X_{1} \times \dots \times X_{n}$ の閉集合であるから， $(X_{i}^{'})_{i \in [n]}$ は $X_{1} \lor \dots \lor X_{n}$ の有限閉被覆である．そこで各 $i \in [n]$ に対して連続写像 $f_{i} : X_{i}^{'} \to ⋁ X_{∙}$ を
$f_{i} (x) = q (i, x_{i})$
で定めると，これらは $X_{i}^{'} \cap X_{j}^{'} = {(x_{1, 0}, \dots, x_{n, 0})}$ 上で貼り合わさって連続写像
$f : X_{1} \lor \dots \lor X_{n} \to ⋁ X_{∙}$
を定める．
各 $i \in [n]$ に対して連続写像 $g_{i} : X_{i} \to X_{1} \lor \dots \lor X_{n}$ を
$g_{i} (x_{i}) = (x_{1, 0}, \dots, x_{i - 1, 0}, x_{i}, x_{i + 1, 0}, \dots, x_{n, 0})$
で定めると， $(g_{i})_{i \in [n]}$ は基点つき空間のあいだの連続写像族なので，楔和の普遍性より連続写像
$g : ⋁ X_{∙} \to X_{1} \lor \dots \lor X_{n}$
が定まる．

こうして定まる $f, g$ が互いの逆写像であることは明らかであろう．

縮積

$(X_{1}, x_{1, 0}), \dots, (X_{n}, x_{n, 0})$ を基点つき空間とする． $X_{1} \times \dots \times X_{n}$ の部分集合
$⋃_{i \in [n]} X_{1} \times \dots \times X_{i - 1} \times {x_{i, 0}} \times X_{i + 1} \times \dots \times X_{n}$
を一点につぶして得られる空間を $X_{1}, \dots, X_{n}$ の縮積（smash product）といい， $X_{1} \land \dots \land X_{n}$ で表わす．縮積は $q_{X_{1} \land \dots \land X_{n}} (x_{1, 0}, \dots, x_{n, 0})$ を基点とする基点つき空間とみなす．

とくに $n = 2$ のとき
$X \land Y = (X \times Y) / (X \lor Y)$
となる．
積空間の可換性より，縮積の可換性がしたがう．
$X_{1}, \dots, X_{n}$ が正則空間ならば，縮積 $X_{1} \land \dots \land X_{n}$ はハウスドルフ空間である（命題2.27，命題5.7の系）．
$X_{1} \times \dots \times X_{n}$ が正規空間ならば，縮積 $X_{1} \land \dots \land X_{n}$ は正規空間である（命題5.14の系）．

縮積と被約錐・被約懸垂

$(X, x_{0})$ を基点つき空間とする．このとき次が成り立つ：

$(S^{0}, - 1)$ との縮積 $S^{0} \land X$ は $X$ と同相である；
$(I, 0)$ との縮積 $I \land X$ は被約錐 $\hat{C} X$ に一致する；
$(S^{1}, s)$ との縮積 $S^{1} \land X$ は被約懸垂 $Σ X$ と同相である．

連続写像
$S^{0} \times X = {- 1} \times X \cup {1} \times X = X ⨿ X \overset{c_{x_{0}} ⨿ {id}_{X}}{\to} X$
は連続写像 $S^{0} \land X \to X$ を誘導する．連続写像 $X \to S^{0} \land X; x \mapsto q_{S^{0} \land X} (1, x)$ が逆写像を与える．
$I \lor X = I \times {x_{0}} \cup {0} \times X$ より，
$I \land X = \frac{I \times X}{I \times {x_{0}} \cup {0} \times X} = \hat{C} X$
が成り立つ．
連続写像 $f : (J, - 1) \to (S^{1}, s); t \mapsto s \cdot \exp (π \sqrt{- 1} (t + 1))$ は同相 $J / {- 1, 1} \approx S^{1}$ を誘導する．また，定理4.11の系より $g := f \times {id}_{X} : J \times X \to S^{1} \times X$ は全射等化写像である．したがって $q_{S^{1} \land X} \circ g : J \times X \to S^{1} \land X$ は全射等化写像であり，
$R (q_{S^{1} \land X} \circ g) = R (J \times {x_{0}} \cup {- 1, 1} \times X)$
が成り立つことがわかるので，同相
$Σ X = \frac{J \times X}{J \times {x_{0}} \cup {- 1, 1} \times X} \approx S^{1} \land X$
が成り立つ．
$J \times X f \times {id}_{X} q_{Σ X} S^{1} \times X q_{S^{1} \land X} Σ X \approx S^{1} \land X$

基点つき空間のあいだの連続写像の族 $(f_{i} : (X_{i}, x_{i, 0}) \to (Y_{i}, y_{i, 0}))_{i \in [n]}$ は連続写像
$f_{1} \land \dots \land f_{n} : X_{1} \land \dots \land X_{n} \to Y_{1} \land \dots \land Y_{n}$
を誘導する．

各 $i \in [n]$ に対して
$(f_{1} \times \dots \times f_{n}) (X_{1} \times \dots \times X_{i - 1} \times {x_{i, 0}} \times X_{i + 1} \times \dots \times X_{n}) \subset Y_{1} \times \dots \times Y_{i - 1} \times {y_{i, 0}} \times Y_{i + 1} \times \dots \times Y_{n}$
が成り立つので，命題5.3より結論を得る．

$(X, x_{0}), (Y, y_{0})$ を基点つき空間とし， $x_{0} \in A \in τ^{c} (X), y_{0} \in B \in τ^{c} (Y)$ とする．このとき次が成り立つ：

$(A, x_{0})$ と $(B, y_{0})$ の縮積 $A \land B$ は $X \land Y$ の閉部分空間と同相である；
$X$ がコンパクトハウスドルフ空間である（resp. $Y$ が局所コンパクトハウスドルフ空間である）ならば，同相 $(X \land Y) / (A \land Y) \approx (X / A) \land Y$ が成り立つ．ただし， $X / A$ は $q_{X / A} (x_{0})$ を基点とする基点つき空間とみなす．

$X \lor Y \in τ^{c} (X \times Y), (A \times B) \cap (X \lor Y) = A \lor B$ であり，仮定より $A \times B \in τ^{c} (X \times Y)$ であるから，命題5.13の系より結論を得る．
補題19より，連続写像 $q_{X / A} \times {id}_{Y} : X \times Y \to (X / A) \times Y$ は連続写像 $q_{X / A} \land {id}_{Y} : X \land Y \to (X / A) \land Y$ を誘導する．仮定より $q_{X / A} \times {id}_{Y}$ は全射等化写像であるから（定理4.11の系）， $q_{X / A} \land {id}_{Y}$ は全射等化写像であり（定理3.7の系），したがって同相
$(X \land Y) / R (q \land {id}_{Y}) \approx (X / A) \land Y$
が成り立つ．
$X \times Y q_{X / A} \times {id}_{Y} q_{X \land Y} (X / A) \times Y q_{(X / A) \land Y} X \land Y q_{X / A} \land {id}_{Y} (X / A) \land Y$
ところで，同一視 $A \land Y \subset X \land Y$ のもとで
$R (q_{X / A} \land {id}_{Y}) = R (A \land Y)$
が成り立つことがわかるので，結論を得る．

$(X_{1}, x_{1, 0}), \dots, (X_{n}, x_{n, 0})$ を基点つき空間とし，各 $i \in [n]$ に対して $A_{i} \subset X_{i}$ を $x_{i, 0} \in A_{i}$ なる部分集合とする．このとき， $f := \prod_{i \in [n]} q_{X_{i} / A_{i}} : \prod_{i \in [n]} X_{i} \to \prod_{i \in [n]} X_{i} / A_{i}$ が等化写像ならば，同相
$X := \frac{X_{1} \times \dots \times X_{n}}{⋃_{i \in [n]} X_{1} \times \dots \times X_{i - 1} \times A_{i} \times X_{i + 1} \times \dots \times X_{n}} \approx \frac{X_{1}}{A_{1}} \land \dots \land \frac{X_{n}}{A_{n}}$
が成り立つ．

任意の $x \in X_{1} \times \dots \times X_{n}$ に対して
$\begin{aligned} x \in ⋃_{i \in [n]} X_{1} \times \dots \times X_{i - 1} \times A_{i} \times X_{i + 1} \times \dots \times X_{n} \\ ⟺ & f (x) \in ⋃_{i \in [n]} \frac{X_{1}}{A_{1}} \times \dots \times \frac{X_{i - 1}}{A_{i - 1}} \times {q_{X_{i} / A_{i}} (x_{i, 0})} \times \frac{X_{i + 1}}{A_{i + 1}} \times \dots \times \frac{X_{n}}{A_{n}} \end{aligned}$
が成り立つので，全射連続写像 $f$ は全単射連続写像
$\overset{―}{f} : X \to \frac{X_{1}}{A_{1}} \land \dots \land \frac{X_{n}}{A_{n}}$
を誘導する：
$X_{1} \times \dots \times X_{n} f quoti. \frac{X_{1}}{A_{1}} \times \dots \times \frac{X_{n}}{A_{n}} quoti. X \overset{―}{f} \frac{X_{1}}{A_{1}} \land \dots \land \frac{X_{n}}{A_{n}}$
いま，仮定より $f$ は等化写像なので，逆写像 ${\overset{―}{f}}^{- 1}$ は連続である．

命題21の仮定が成り立つための十分条件として，たとえば次のものがある：

$X_{1}, \dots, X_{n - 1}$ がコンパクト空間であり， $X_{1} / A_{1}, \dots, X_{n - 1} / A_{n - 1}$ がハウスドルフ空間である；
$n = 2$ で， $X_{i}, X_{3 - i} / A_{3 - i}$ がともに局所コンパクトハウスドルフ空間である．

縮積の結合性

$(X, x_{0}), (Y, y_{0}), (Z, z_{0})$ を基点つき空間とする．

$X, Y$ はコンパクトハウスドルフ空間；
$Y, Z$ はコンパクトハウスドルフ空間；
$X, Z$ は局所コンパクトハウスドルフ空間

のいづれかが成り立つならば，同相
$X \land Y \land Z \approx X \land (Y \land Z) \approx (X \land Y) \land Z$
が成り立つ．

全射連続写像

$q_{0} := q_{X \land Y \land X} : X \times Y \times Z \to X \land Y \land Z$ ;
$q_{1} := q_{X \land (Y \land Z)} \circ ({id}_{X} \times q_{Y \land Z}) : X \times (Y \times Z) \to X \land (Y \land Z)$ ;
$q_{2} := q_{(X \land Y) \land Z} \circ (q_{X \land Y} \times {id}_{Z}) : (X \times Y) \times Z \to (X \land Y) \land Z$

を考える．

$q_{1}$ は全射等化写像である．また， $q_{X \land Y}$ はコンパクト空間 $X \times Y$ からハウスドルフ空間 $X \land Y$ への全射連続写像であるから， $q_{2}$ は全射等化写像である．
(1)と同様．
$X$ が局所コンパクトハウスドルフ空間であることから $q_{1}$ が， $Z$ が局所コンパクトハウスドルフ空間であることから $q_{2}$ が全射等化写像であることがしたがう．

いづれも定理4.11の系および定理3.7の系による．さらに， $R (q_{0}), R (q_{1}), R (q_{2})$ はいづれも
$R (({x_{0}} \times Y \times Z) \cup (X \times {y_{0}} \times Z) \cup (X \times Y \times {z_{0}}))$
に一致するので，恒等写像が所期の同相を誘導する：
$X \times Y \times Z id q_{0} X \times (Y \times Z) id q_{1} (X \times Y) \times Z q_{2} X \land Y \land Z \approx X \land (Y \land Z) \approx (X \land Y) \land Z$

多重懸垂

$(X, x_{0})$ を基点つき空間とする．非負整数 $n \in Z_{\geq 0}$ に対して
$\begin{aligned} Σ^{0} X & = X, \\ Σ^{n} X & = Σ (Σ^{n - 1} X), n > 0 \end{aligned}$
と定める．このとき，任意の $n \in Z_{\geq 0}$ に対して
$Σ^{n} X \approx S^{n} \land X$
が成り立つ．実際，命題18より
$Σ^{0} X = X \approx S^{0} \land X$
であり， $n > 0$ のとき， $S^{1}, S^{n - 1}$ がコンパクトハウスドルフ空間であることから
$\begin{aligned} Σ^{n} X & = Σ (Σ^{n - 1} X) \\ \approx S^{1} \land Σ^{n - 1} X \\ \approx S^{1} \land (S^{n - 1} \land X) \\ \approx (S^{1} \land S^{n - 1}) \land X \\ \approx Σ S^{n - 1} \land X \\ \approx S^{n} \land X \end{aligned}$
が成り立つ．

命題22により命題14の別証明が得られる：

命題22の

基点つき空間 $(X, x_{0})$ に対して，同相
$\hat{C} Σ X \approx Σ \hat{C} X$
が成り立つ．

$I, S^{1}$ はコンパクトハウスドルフ空間であるから，命題18と合わせて
$\hat{C} Σ X \approx I \land (S^{1} \land X) \approx (I \land S^{1}) \land X \approx (S^{1} \land I) \land X \approx S^{1} \land (I \land X) \approx Σ \hat{C} X$
を得る．

命題22は次の形に一般化できる：

縮積の結合性

$(X_{1}, x_{1, 0}), \dots, (X_{n}, x_{n, 0})$ を基点つき空間とし， $m \in [n - 1]$ とする．このとき $X_{1} \land \dots \land X_{m}$ または $X_{m + 1} \land \dots \land X_{n}$ が局所コンパクトハウスドルフ空間ならば，同相
$X_{1} \land \dots \land X_{n} \approx (X_{1} \land \dots \land X_{m}) \land (X_{m + 1} \land \dots \land X_{n})$
が成り立つ．

$q_{n} : X_{1} \times \dots \times X_{n} \to X_{1} \land \dots \land X_{n}$
$q_{m} : X_{1} \times \dots \times X_{m} \to X_{1} \land \dots \land X_{m}$
$q_{n - m} : X_{m + 1} \times \dots \times X_{n} \to X_{m + 1} \land \dots \land X_{n}$
$q_{m, n - m} : (X_{1} \land \dots \land X_{m}) \times (X_{m + 1} \land \dots \land X_{n}) \to (X_{1} \land \dots \land X_{m}) \land (X_{m + 1} \land \dots \land X_{n})$

を商写像とする．仮定より $q_{m} \times q_{n - m}$ は全射等化写像であるから（定理4.11の系），合成 $q := q_{m, n - m} \circ (q_{m} \times q_{n - m})$ は全射等化写像である．同値関係 $R (q)$ は $X_{1} \times \dots \times X_{n}$ の部分集合
$\begin{aligned} (⋃_{i \in [m]} X_{1} \times \dots \times X_{i - 1} \times {x_{i, 0}} \times X_{i + 1} \times \dots \times X_{m}) \times X_{m + 1} \times \dots \times X_{n} \\ \cup X_{1} \times \dots \times X_{m} \times (⋃_{i \in [n - m]} X_{m + 1} \times \dots \times X_{m + i - 1} \times {x_{m + i, 0}} \times X_{m + i + 1} \times \dots \times X_{n}) \\ = & ⋃_{i \in [n]} X_{1} \times \dots \times X_{i - 1} \times {x_{i, 0}} \times X_{i + 1} \times \dots \times X_{n} \end{aligned}$
を一点につぶす同値関係に一致するので，
$X_{1} \land \dots \land X_{n} = \frac{X_{1} \times \dots \times X_{n}}{R (q)} \approx (X_{1} \land \dots \land X_{m}) \land (X_{m + 1} \land \dots \land X_{n})$
が成り立つ．
$X_{1} \times \dots \times X_{m} \times X_{m + 1} \times \dots \times X_{n} q_{m} \times q_{n - m} q_{n} (X_{1} \land \dots \land X_{m}) \times (X_{m + 1} \land \dots \land X_{n}) q_{m, n - m} X_{1} \land \dots \land X_{m} \land X_{m + 1} \land \dots \land X_{n} \approx (X_{1} \land \dots \land X_{m}) \land (X_{m + 1} \land \dots \land X_{n})$

命題23の証明よりつぎがわかる：任意の $m \in [n - 1]$ に対して，全射連続写像 $q_{m} \times q_{n - m}$ は全単射連続写像
$X_{1} \land \dots \land X_{n} \to (X_{1} \land \dots \land X_{m}) \land (X_{m + 1} \land \dots \land X_{n})$
を誘導する．

円周の縮積

$n$ 個の円周 $S^{1}$ の縮積は $n$ 次元球面 $S^{n}$ に同相である．実際， $S^{1}$ は局所コンパクトハウスドルフ空間であるから，命題23と $n \in Z_{\geq 1}$ に関する数学的帰納法により
$\underset{n}{\underset{⏟}{S^{1} \land \dots \land S^{1}}} \approx S^{1} \land (\underset{n - 1}{\underset{⏟}{S^{1} \land \dots \land S^{1}}}) \approx S^{1} \land S^{n - 1} \approx Σ S^{n - 1} \approx S^{n}$
が成り立つ．

縮積と被約懸垂

$(X, x_{0}), (Y, y_{0})$ を基点つき空間とする．

$X$ はコンパクトハウスドルフ空間；
$Y$ は局所コンパクトハウスドルフ空間

のいづれかが成り立つならば，同相
$Σ (X \land Y) \approx Σ X \land Y$
が成り立つ．

全射連続写像

$q_{1} := q_{Σ (X \land Y)} \circ ({id}_{J} \times q_{X \land Y}) : J \times (X \times Y) \to Σ (X \land Y)$
$q_{2} := q_{Σ X \land Y} \circ (q_{Σ X} \times {id}_{Y}) : (J \times X) \times Y \to Σ X \land Y$

を考える． $J = [- 1, 1]$ はコンパクトハウスドルフ空間なので， $q_{1}$ は全射等化写像である．

$q_{Σ X}$ はコンパクト空間 $J \times X$ からハウスドルフ空間 $Σ X$ への全射連続写像なので， $q_{2}$ は全射等化写像である．
$Y$ の局所コンパクト性より $q_{Σ X} \times {id}_{Y}$ は全射等化写像なので， $q_{2}$ は全射等化写像である．

$R (q_{1}), R (q_{2})$ はいづれも
$R (({- 1, 1} \times X \times Y) \cup (J \times {x_{0}} \times Y) \cup (J \times X \times {y_{0}}))$
に一致するので，恒等写像が所期の同相を誘導する：
$J \times (X \times Y) id q_{1} (J \times X) \times Y q_{2} Σ (X \land Y) \approx Σ X \land Y$

命題24の

$(X, x_{0}), (Y, y_{0})$ を基点つき空間とする． $X, Y$ がともに局所コンパクトハウスドルフ空間ならば，同相
$Σ X \land Y \approx X \land Σ Y$
が成り立つ．

命題24と縮積の可換性より
$Σ X \land Y \approx Σ (X \land Y) \approx Σ (Y \land X) \approx Σ Y \land X \approx X \land Σ Y$
が成り立つ．

球面の縮積

非負整数 $m, n \in Z_{\geq 0}$ に対して，同相
$S^{m} \land S^{n} \approx S^{m + n}$
が成り立つ．実際，命題18，例7と $m \in Z_{\geq 0}$ に関する数学的帰納法により
$\begin{aligned} S^{m} \land S^{n} & \approx Σ S^{m - 1} \land S^{n} \\ \approx Σ (S^{m - 1} \land S^{n}) \\ \approx Σ S^{(m - 1) + n} = Σ S^{m + n - 1} \\ \approx S^{m + n} \end{aligned}$
が成り立つ．或いは例9と命題23より
$\begin{aligned} S^{m} \land S^{n} & \approx (\underset{m}{\underset{⏟}{S^{1} \land \dots \land S^{1}}}) \land (\underset{n}{\underset{⏟}{S^{1} \land \dots \land S^{1}}}) \\ \approx \underset{m + n}{\underset{⏟}{S^{1} \land \dots \land S^{1}}} \\ \approx S^{m + n} \end{aligned}$
を得る．

参考文献

[1]

N. Bourbaki, General Topology Chapters 1--4

[2]

J. Dugundji, Topology

[3]

小松醇郎，中岡稔，菅原正博, 『位相幾何学 I』, 岩波書店

投稿日：2023年11月14日

更新日：2023年12月1日

この本を高評価した人

高評価したユーザはいません

この本に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

うすい

11920

位相空間論に興味があります．

他の人のコメント

コメントはありません。

読み込み中

うすい

New Spaces from Old

現在のページ

商空間の例

錐
懸垂
結
結の結合性について
等化結と誘導結
誘導結の結合性
等化結の結合性：コンパクトハウスドルフ空間の場合
等化結の結合性：局所コンパクトハウスドルフ空間の場合（未）
基点つき空間
被約錐・被約懸垂
楔和
縮積
参考文献

前のページへ

6 / 7

次のページへ

前ページへ

次ページへ

商空間の例

錐

懸垂

結

結の結合性について

等化結と誘導結

誘導結の結合性

連続写像f:X′∘X″→X1∘⋯∘Xnの構成

連続写像g:X1∘⋯∘Xn→X′∘X″の構成

f,gが互いの逆写像であること

等化結の結合性：コンパクトハウスドルフ空間の場合

等化結の結合性：局所コンパクトハウスドルフ空間の場合（未）

基点つき空間

被約錐・被約懸垂

楔和

x∈iλ(Xλ∖{xλ,0}),y=iμ(xμ,0)のとき

x∈iλ(Xλ∖{xλ,0}),y∈iμ(Xμ∖{xμ,0})のとき

縮積

参考文献

この本を高評価した人

この本に送られたバッジ

投稿者

コメント

他の人のコメント

連続写像 $f : X^{'} \circ X^{″} \to X_{1} \circ \dots \circ X_{n}$ の構成

連続写像 $g : X_{1} \circ \dots \circ X_{n} \to X^{'} \circ X^{″}$ の構成

$f, g$ が互いの逆写像であること

$x \in i_{λ} (X_{λ} ∖ {x_{λ, 0}}), y = i_{μ} (x_{μ, 0})$ のとき

$x \in i_{λ} (X_{λ} ∖ {x_{λ, 0}}), y \in i_{μ} (X_{μ} ∖ {x_{μ, 0}})$ のとき