文献あり

商空間

2074

商空間

$(X, τ (X))$ を位相空間とし， $R \subset X \times X$ を $X$ 上の同値関係とする．このとき，商写像 $q_{R} : X \to X / R$ による等化位相 $τ (q_{R})$ を（ $R$ による）商位相（quotient topology）といい，位相空間 $(X / R, τ (q_{R}))$ を（ $R$ による）商空間（quotient space）という．

商空間の

T_{1}

性

$q_{R}^{- 1} (q_{R} (x)) = R (x)$ より，次は同値である：

$X / R$ は $T_{1}$ 空間である；
任意の $x \in X$ に対して $R (x) \subset X$ は閉集合である．

等化空間の普遍性よりただちに次を得る：

商空間の普遍性

$X$ を位相空間とし， $R \subset X \times X$ を $X$ 上の同値関係とする．また， $Y$ を位相空間， $f : X \to Y$ を連続写像とする．このとき，任意の $x, x^{'} \in X$ に対して
$(x, x^{'}) \in R ⟹ f (x) = f (x^{'})$
が成り立つならば，連続写像 $\overset{―}{f} : X / R \to Y$ であって $\overset{―}{f} \circ q_{R} = f$ を満たすものがただ一つ存在する．
$X f q_{R} Y X / R \overset{―}{f}$

（cf. 補題3.20）

定義より商写像は全射等化写像である．逆に，全射等化写像は次の意味で商写像である： $f : X \to Y$ を全射等化写像とする．このとき， $X$ 上の同値関係 $R (f) \subset X \times X$ を
$R (f) = {(x, x^{'}) \in X \times X ∣ f (x) = f (x^{'})}$
で定めると，定理1より，全単射連続写像 $\overset{―}{f} : X / R (f) \to Y$ が存在することがわかる：
$X f q_{R (f)} Y X / R (f) \overset{―}{f}$
いま $f$ は等化写像なので， ${\overset{―}{f}}^{- 1} \circ f = q_{R (f)}$ の連続性から ${\overset{―}{f}}^{- 1}$ の連続性がしたがう．よって $\overset{―}{f} : X / R (f) \to Y$ は同相写像である．

全射連続開写像（resp. 閉写像）は全射等化写像であったから（命題3.3），ただちに次を得る：

$f : X \to Y$ を全射連続開写像（resp. 閉写像）とする．このとき
$\overset{―}{f} : X / R (f) \to Y$ は同相写像である．

（積の商と商の積）

$(X_{λ})_{λ \in Λ}$ を位相空間族とし，各 $λ \in Λ$ に対して $R_{λ} \subset X_{λ} \times X_{λ}$ を同値関係とする．積空間 $\prod X_{∙}$ 上の同値関係 $\prod R_{∙}$ を次で定める：
$\prod R_{∙} = {(x, x^{'}) \in \prod X_{∙} \times \prod X_{∙} | \forall λ \in Λ, (x_{λ}, x_{λ}^{'}) \in R_{λ}} .$
このとき，各 $λ \in Λ$ に対して商写像 $q_{λ} : X_{λ} \to X_{λ} / R_{λ}$ が開写像ならば，同相
$\prod X_{∙} / \prod R_{∙} \approx \prod_{λ \in Λ} X_{λ} / R_{λ}$
が成り立つ．

仮定より，商写像族の積
$q := \prod q_{∙} : \prod X_{∙} \to \prod_{λ \in Λ} X_{λ} / R_{λ}$
は全射連続開写像であり， $R (q) = \prod R_{∙}$ が成り立つ．

商空間の普遍性より，次が成り立つ：

$f : X \to Y$ を連続写像とし， $R \subset X \times X, S \subset Y \times Y$ を同値関係とする．このとき，任意の $x, x^{'} \in X$ に対して
$(x, x^{'}) \in R ⟹ (f (x), f (x^{'})) \in S$
が成り立つならば，連続写像 $\overset{―}{f} : X / R \to Y / S$ であって $\overset{―}{f} \circ q_{R} = q_{S} \circ f$ を満たすものがただ一つ存在する．
$X f q_{R} Y q_{S} X / R \overset{―}{f} Y / S$

（商空間の推移性）

$X$ を位相空間， $R, S \subset X \times X$ を同値関係とする．このとき， $R \subset S$ が成り立つならば， $X / R$ 上の同値関係 $S / R$ であって同相 $(X / R) / (S / R) \approx X / S$ が成り立つものがただ一つ存在する．

仮定より，連続写像 $\overset{―}{{id}_{X}} : X / R \to X / S$ が存在する：
$X {id}_{X} q_{R} X q_{S} X / R \overset{―}{{id}_{X}} X / S$
いま， $\overset{―}{{id}_{X}} \circ q_{R} = q_{S}$ は全射等化写像であるから， $\overset{―}{{id}_{X}}$ も全射等化写像である（定理3.7の系）．そこで $S / R = R (\overset{―}{{id}_{X}})$ とおくと，同相 $(X / R) / (S / R) \approx X / S$ が成り立つ．

商空間の部分集合

$X$ を位相空間， $R \subset X \times X$ を同値関係とし， $C \subset X / R$ とする．このとき，

$C \in τ (X / R)$ ;
$q := q_{R} : X \to X / R : open$ ;
$C \in τ^{c} (X / R)$ ;
$q : X \to X / R : closed$

のいづれかが成り立つならば， $B := q^{- 1} (C)$ 上の同値関係
$R | B := R \cap (B \times B)$
による商空間 $B / (R | B)$ と $C$ とは同相である．

仮定より $q^{C} : q^{- 1} (C) \to C$ は全射等化写像である（命題3.9）．よって
$q^{- 1} (C) / R (q^{C}) \approx C$
が成り立つ．ところで，任意の $x, x^{'} \in q^{- 1} (C)$ に対して
$(x, x^{'}) \in R (q^{C}) ⟺ (x, x^{'}) \in R | q^{- 1} (C)$
が成り立つので，結論を得る．

部分集合を一点につぶして得られる空間

$X$ を位相空間とし， $A \subset X$ を非空部分集合とする．このとき， $X$ 上の同値関係
$R (A) := Δ_{X} \cup (A \times A) \subset X \times X$
による商空間を $A$ を一点につぶして得られる空間といい， $X / A$ で表わす．

$n$ 次元球体 $D^{n}$ の境界 $S^{n - 1}$ を一点につぶして得られる空間 $D^{n} / S^{n - 1}$ は $n$ 次元球面 $S^{n} \subset R^{n} \times R$ に同相である．

連続写像
$f : D^{n} \to S^{n}; x \mapsto (2 x \sqrt{1 - ∥ x ∥^{2}}, 2 ∥ x ∥^{2} - 1)$
を考える．

$x \in S^{n - 1} ⟺ f (x) = (0, \dots, 0, 1) =: N$ が成り立つ；
$f |_{D^{n} ∖ S^{n - 1}}^{S^{n} ∖ {N}}$ は同相写像
$int (D^{n}) \to R^{n}; x \mapsto \frac{x}{\sqrt{1 - ∥ x ∥^{2}}}$
と立体射影の逆写像
$R^{n} \to S^{n} ∖ {N}; y \mapsto (\frac{2 y}{∥ y ∥^{2} + 1}, \frac{∥ y ∥^{2} - 1}{∥ y ∥^{2} + 1})$
の合成ゆえ同相写像である．

したがって，任意の $x, x^{'} \in D^{n}$ に対して
$q_{D^{n} / S^{n - 1}} (x) = q_{D^{n} / S^{n - 1}} (x^{'}) ⟺ f (x) = f (x^{'})$
が成り立つので， $f$ は全単射連続写像 $\overset{―}{f} : D^{n} / S^{n - 1} \to S^{n}$ を誘導する．いま $D^{n} / S^{n - 1}$ はコンパクトであり $S^{n}$ はハウスドルフであるから， $\overset{―}{f}$ は同相写像である．

命題4の

$X$ を位相空間とし， $A \subset B \subset X$ とする．このとき

$B \in τ (X)$ ;
$q_{X / A} : X \to X / A : open$ ;
$B \in τ^{c} (X)$ ;
$q_{X / A} : X \to X / A : closed$

のいづれかが成り立つならば， $B / A$ と $q_{X / A} (B)$ とは同相である．

$C = q_{X / A} (B) \subset X / A$ とおくと， $A \subset B$ より $B = (q_{X / A})^{- 1} (C)$ が成り立つ．
$R (A) | B = Δ_{B} \cup (A \times A)$ が成り立つ．

商空間の推移性より次を得る：

「もうちょっとつぶす」

=

「はじめから全部つぶす」

$X$ を位相空間とし， $A, B \subset X$ とする．このとき， $A \cap B \neq \emptyset$ が成り立つならば， $X / A$ の部分集合 $q_{X / A} (B)$ を一点につぶして得られる空間 $(X / A) / q_{X / A} (B)$ は $X / (A \cup B)$ に同相である．

商空間の推移性より
$(X / A) / (R (A \cup B) / R (A)) \approx X / (A \cup B)$
が成り立つので， $R (A \cup B) / R (A) = R (q_{X / A} (B))$ を示せばよい．

$R (A \cup B) / R (A) \subset R (q_{X / A} (B))$

$(q_{X / A} (x), q_{X / A} (y)) \in R (A \cup B) / R (A)$ とする．このとき， $q_{X / A \cup B} (x) = q_{X / A \cup B} (y)$ より
$(x, y) \in R (A \cup B) = Δ_{X} \cup ((A \cup B) \times (A \cup B))$
が成り立つ．

$(x, y) \in Δ_{X}$ のとき，明らかに $(q_{X / A} (x), q_{X X / A} (y)) \in R (q_{X / A} (B))$ が成り立つ．
$(x, y) \in A \times A$ のとき， $(q_{X / A} (x), q_{X / A} (y)) \in Δ_{X / A} \subset R (q_{X / A} (B))$ が成り立つ．
$(x, y) \in A \times B$ のとき， $z \in A \cap B$ を取ると，
$(q_{X / A} (x), q_{X / A} (y)) = (q_{X / A} (z), q_{X / A} (y)) \in q_{X / A} (B) \times q_{X / A} (B) \subset R (q_{X / A} (B))$
が成り立つことがわかる．
$(x, y) \in B \times A$ のときも同様．
$(x, y) \in B \times B$ のとき，明らかに $(q_{X / A} (x), q_{X / A} (y)) \in R (q_{X / A} (B))$ が成り立つ．

$R (q_{X / A} (B)) \subset R (A \cup B) / R (A)$

$(q_{X / A} (x), q_{X / A} (y)) \in R (q_{X / A} (B))$ とする．このとき， $q_{X / A \cup B} (x) = q_{X / A \cup B} (y)$ が成り立つことを示せばよい．

$(q_{X / A} (x), q_{X / A} (y)) \in Δ_{X / A}$ のとき，
$(x, y) \in R (A) \subset R (A \cup B)$
より $q_{X / A \cup B} (x) = q_{X / A \cup B} (y)$ を得る．
$(q_{X / A} (x), q_{X / A} (y)) \in q_{X / A} (B) \times q_{X / A} (B)$ のとき， $x^{'}, y^{'} \in B$ であって $q_{X / A} (x) = q_{X / A} (x^{'}), q_{X / A} (y) = q_{X / A} (y^{'})$ となるものが存在するので，前段と $x^{'}, y^{'} \in A \cup B$ より
$q_{X / A \cup B} (x) = q_{X / A \cup B} (x^{'}) = q_{X / A \cup B} (y^{'}) = q_{X / A \cup B} (y)$
を得る．

商写像 $q := q_{X / A} : X \to X / A$ について，次が成り立つ：

$A \in τ (X)$ ならば， $q_{X / A}$ は開写像である；
$A \in τ^{c} (X)$ ならば， $q_{X / A}$ は閉写像である．

よって $A \in τ (X) \cup τ^{c} (X)$ ならば， $A$ を含むような任意の部分集合 $B \subset X$ に対して， $B / A$ と $q_{X / A} (B)$ とは同相である．

任意の部分集合 $B \subset X$ に対して
$q^{- 1} (q (B)) = {\begin{cases} A \cup B & , A \cap B \neq \emptyset \\ B & , A \cap B = \emptyset \end{cases}$
が成り立つので，等化位相の定義より結論を得る．後半は命題4の系よりしたがう．

つぶしていないところはつぶれていない

$A \in τ (X) \cup τ^{c} (X)$ ならば
$(q_{X / A})^{(X / A) ∖ q_{X / A} (A)} : X ∖ A \to (X / A) ∖ q_{X / A} (A)$
は同相写像である．

$(q_{X / A})^{- 1} ((X / A) ∖ q_{X / A} (A)) = X ∖ A$ に注意する．

仮定より $q := q_{X / A}$ は開写像（resp. 閉写像）であるから，補題3.8より， $q^{(X / A) ∖ q (A)}$ は開写像（resp. 閉写像）である．また， $q^{(X / A) ∖ q (A)}$ は明らかに全単射である．よって，全単射連続開写像（resp. 閉写像） $q^{(X / A) ∖ q (A)}$ は同相写像である．

$X ∖ A$ と $(X / A) ∖ q (A)$ とは一般には同相ではない．実際，

$X = {0, 1, 2, 3}$
$τ (X) = {\emptyset, {1, 2}, X}$
$A = {2, 3} \notin τ (X) \cup τ^{c} (X)$

を考えると， ${1} = {1, 2} \cap (X ∖ A) \subset X ∖ A$ は開集合だが， $τ (X / A) = {\emptyset, X / A}$ より $q ({1}) \subset (X / A) ∖ q (A)$ は開集合ではないことがわかる．

命題7の

$X$ を $T_{3}$ 空間（たとえば局所コンパクトハウスドルフ空間）とする．このとき，任意の閉集合 $A \subset X$ に対して， $X / A$ はハウスドルフ空間である．

商写像を $q : X \to X / A$ とおく． $X ∖ A \in τ (X)$ より $(X / A) ∖ q (A) \in τ (X / A)$ ，したがって $τ (X / A) | ((X / A) ∖ q (A)) \subset τ (X / A)$ となることに注意する（命題2.4の系）．
$x, y \in X$ とし， $q (x) \neq q (y)$ とする．

$x, y \notin A$ のとき，ハウスドルフ空間 $X ∖ A$ における相異なる2点 $x, y$ の交わらない開近傍の $q$ による像が， $(X / A) ∖ q (A)$ における，したがって $X / A$ における $q (x), q (y)$ の交わらない開近傍を与える．
$x \notin A, y \in A$ のとき， $U \in τ (x, X), V \in τ (A, X)$ であって $U \cap V = \emptyset$ となるものが存在する．
$q^{- 1} (q (U)) = U, q^{- 1} (q (V)) = V$
より， $q (U), q (V)$ が $X / A$ における $q (x), q (y)$ の交わらない開近傍を与える．

接着空間

$X, Y$ を位相空間， $A \subset X$ を部分集合， $f : A \to Y$ を連続写像とする．このとき，余積空間 $Y ⨿ X$ 上の“関係
$i_{Y} (f (a)) \sim i_{X} (a), a \in A$
によって生成される同値関係”，すなわち同値関係
$\overset{―}{R} (⋃_{λ \in f (A)} {i_{Y} (λ)} \times {i_{X} (a) ∣ a \in f^{- 1} (λ)})$
による商空間を（ $f$ による／ $f$ を接着写像とする）接着空間（attaching space, adjunction space）といい， $Y \cup_{f} X$ で表わす． $f$ が包含写像であるときは $Y \cup_{A} X$ とも書く．また，商写像を $q_{f} : Y ⨿ X \to Y \cup_{f} X$ とおく．
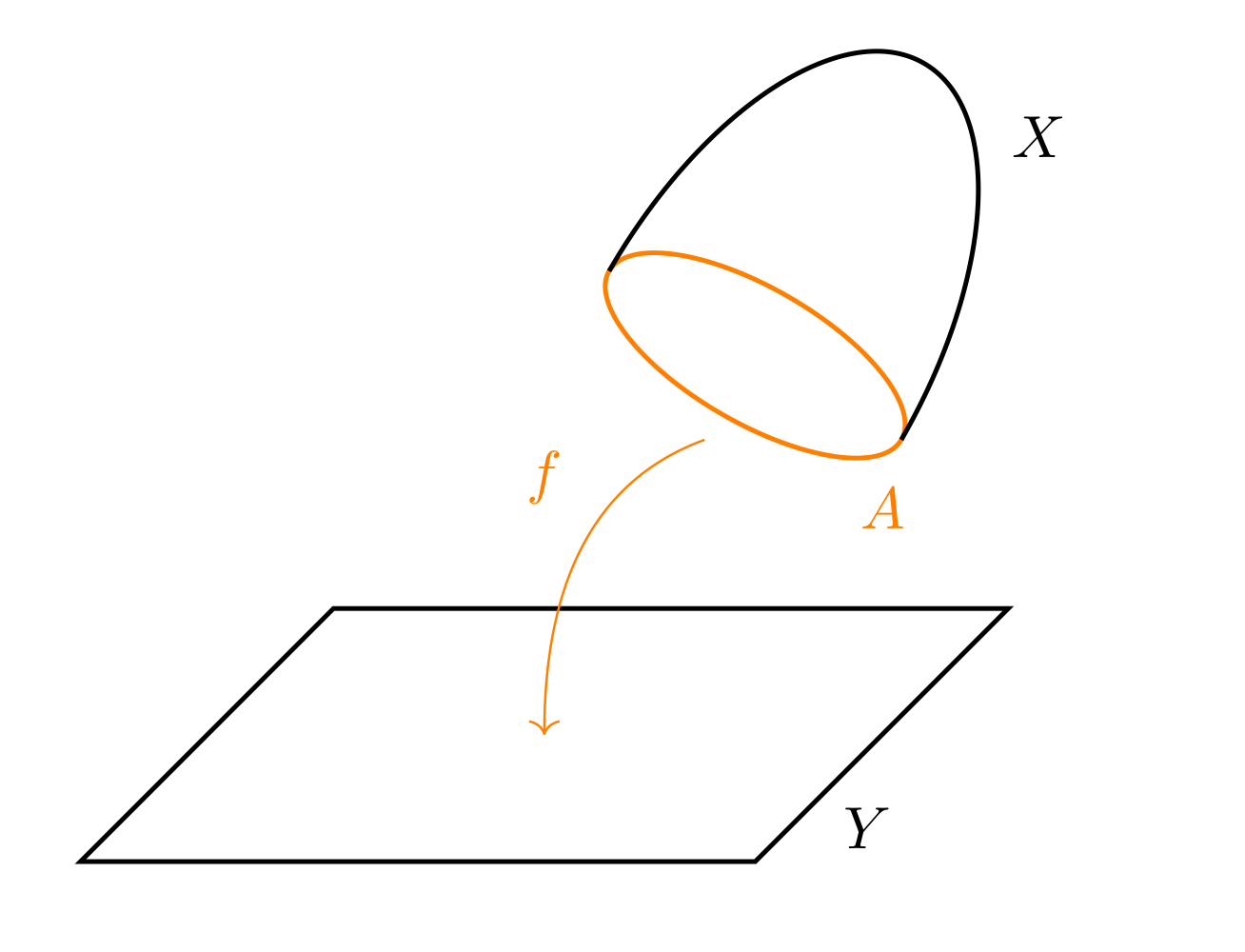接着空間

接着空間の普遍性

（定義3の記号のもとで）任意の位相空間 $Z$ と連続写像 $φ : Y \to Z, ψ : X \to Z$ であって
$\forall a \in A, φ (f (a)) = ψ (a)$
を満たすものに対して，連続写像 $φ \cup_{f} ψ : Y \cup_{f} X \to Z$ であって次の図式を可換にするものがただ一つ存在する．
$A {id}_{A}^{X} f X q_{f} \circ i_{X} ψ Y q_{f} \circ i_{Y} φ Y \cup_{f} X φ \cup_{f} ψ Z$

余積空間 $Y ⨿ X$ の普遍性より，連続写像 $φ ⨿ ψ : Y ⨿ X \to Z$ であって
$(φ ⨿ ψ) \circ i_{Y} = φ, (φ ⨿ ψ) \circ i_{X} = ψ$
を満たすものがただ一つ存在する．
$Y φ i_{Y} Z X ψ i_{X} Z Y ⨿ X φ ⨿ ψ Y ⨿ X φ ⨿ ψ$
仮定より，任意の $a \in A$ に対して
$(φ ⨿ ψ) (i_{Y} (f (a))) = φ (f (a)) = ψ (a) = (φ ⨿ ψ) (i_{X} (a))$
が成り立つので，商空間 $Y \cup_{f} X$ の普遍性より，連続写像 $φ \cup_{f} ψ : Y \cup_{f} X \to Z$ であって
$(φ \cup_{f} ψ) \circ q_{f} = φ ⨿ ψ$
を満たすものがただ一つ存在する．
$Y ⨿ X φ ⨿ ψ q_{f} Z Y \cup_{f} X φ \cup_{f} ψ$
この写像が定理の主張を満たすことは明らかであろう．

位相空間 $X$ の非空部分集合 $A \subset X$ に対して，定値写像 $c : A \to {*}$ による接着空間 ${*} \cup_{c} X$ は $X / A$ に他ならない，すなわち同相 ${*} \cup_{c} X \approx X / A$ が成り立つ． $A$ が空集合のとき， $R (\emptyset) = Δ_{X} = R ({id}_{X})$ より $X / \emptyset \approx X$ となるので $A = \emptyset$ の場合を除外しなくてもよさそうなものだが， $X / \emptyset = {*} ⨿ X$ と解釈したほうが都合がよいと [Switzer] に書いてあった．

以下，

$X, Y$ を位相空間
$A \subset X$ を閉集合
$f : A \to Y$ を連続写像

とする．

任意の $C \subset Y ⨿ X$ に対して

$i_{Y}^{- 1} (q_{f}^{- 1} (q_{f} (C))) = i_{Y}^{- 1} (C) \cup f (i_{X}^{- 1} (C) \cap A)$ ;
$i_{X}^{- 1} (q_{f}^{- 1} (q_{f} (C))) = i_{X}^{- 1} (C) \cup (i_{X}^{- 1} (q_{f}^{- 1} (q_{f} (C))) \cap A)$

が成り立つ．

$D = q_{f}^{- 1} (q_{f} (C)) \subset Y ⨿ X$ とおく．

$\begin{aligned} y \in i_{Y}^{- 1} (D) & ⟺ q_{f} (i_{Y} (y)) \in q_{f} (C) \\ ⟺ \exists c \in C, q_{f} (i_{Y} (y)) = q_{f} (c) \\ ⟺ y \in i_{Y}^{- 1} (C) \cup f (i_{X}^{- 1} (C) \cap A) . \end{aligned}$
$\begin{aligned} x \in i_{X}^{- 1} (D) & ⟺ \exists c \in C, q_{f} (i_{X} (x)) = q_{f} (c) \\ ⟺ x \in i_{X}^{- 1} (C) \cup (i_{X}^{- 1} (D) \cap A) . \end{aligned}$

接着空間の閉集合

部分集合 $C \subset Y ⨿ X$ が $i_{X}^{- 1} (C) \in τ^{c} (X)$ を満たすとする．このとき次は同値である：

$q_{f} (C) \in τ^{c} (Y \cup_{f} X)$ ;
$i_{Y}^{- 1} (C) \cup f (i_{X}^{- 1} (C) \cap A) \in τ^{c} (Y)$ .

$D = q_{f}^{- 1} (q_{f} (C)) \subset Y ⨿ X$ とおく． $A \in τ^{c} (X)$ より $τ^{c} (A) \subset τ^{c} (X)$ に注意する．
$i_{X}^{- 1} (D) \cap A = ({id}_{A}^{X})^{- 1} (i_{X}^{- 1} (D)) = f^{- 1} (i_{Y}^{- 1} (D)) \subset A$
より
$i_{X}^{- 1} (D) = i_{X}^{- 1} (C) \cup f^{- 1} (i_{Y}^{- 1} (D))$
となるので， $i_{X}^{- 1} (C) \in τ^{c} (X)$ のとき
$\begin{aligned} q_{f} (C) \in τ^{c} (Y \cup_{f} X) & ⟺ D \in τ^{c} (Y ⨿ X) \\ ⟺ i_{Y}^{- 1} (D) \in τ^{c} (Y) \land i_{X}^{- 1} (D) \in τ^{c} (X) \\ ⟺ i_{Y}^{- 1} (D) \in τ^{c} (Y) \end{aligned}$
が成り立つことがわかる．

接着空間の開集合

開集合 $U \in τ (X), V \in τ (Y)$ が $f^{- 1} (V) = U \cap A$ を満たすとする．このとき， $q_{f} (V ⨿ U) \in τ (Y \cup_{f} X)$ が成り立つ．

$V ⨿ U \in τ (Y ⨿ X)$ であるから，これが $q_{f}$ 飽和集合であることを示せばよい．ところで， $W = q_{f}^{- 1} (q_{f} (V ⨿ U)) \subset Y ⨿ X$ とおくと，補題9より
$\begin{aligned} i_{Y}^{- 1} (W) & = i_{Y}^{- 1} (V ⨿ U) \cup f (i_{X}^{- 1} (V ⨿ U) \cap A) \\ = V \cup f (U \cap A) \\ = V, \\ i_{X}^{- 1} (W) & = i_{X}^{- 1} (V ⨿ U) \cup f^{- 1} (i_{Y}^{- 1} (W)) \\ = U \cup f^{- 1} (V) \\ = U \end{aligned}$
が成り立つので，
$\begin{aligned} W & = i_{Y} (i_{Y}^{- 1} (W)) \cup i_{X} (i_{X}^{- 1} (W)) \\ = i_{Y} (V) \cup i_{X} (U) \\ = V ⨿ U \end{aligned}$
を得る．

接着空間の部分空間

$Y$ は閉部分空間 $q_{f} \circ i_{Y} (Y) \subset Y \cup_{f} X$ と同相である；
$X ∖ A$ は開部分空間 $q_{f} \circ i_{X} (X ∖ A) \subset Y \cup_{f} X$ と同相である；
$Y \cup_{f} X = q_{f} \circ i_{Y} (Y) \cup q_{f} \circ i_{X} (X ∖ A)$ および $q_{f} \circ i_{Y} (Y) \cap q_{f} \circ i_{X} (X ∖ A) = \emptyset$ が成り立つ．

写像 $(q_{f} \circ i_{Y})^{q_{f} \circ i_{Y} (Y)} : Y \to q_{f} \circ i_{Y} (Y)$ は全単射連続写像であり $i_{Y} : Y \to Y ⨿ X$ は閉写像であるから， $q_{f} | i_{Y} (Y)$ が閉写像であることを示せばよい．そこで $C \in τ^{c} (i_{Y} (Y))$ とすると， $i_{X}^{- 1} (C) = \emptyset \in τ^{c} (X)$ であるから，
$i_{Y}^{- 1} (C) \cup f (i_{X}^{- 1} (C) \cap A) = i_{Y}^{- 1} (C) \in τ^{c} (Y)$
と命題10より $q_{f} (C) \in τ^{c} (Y \cup_{f} X)$ を得る．
写像 $(q_{f} \circ i_{X})^{q_{f} \circ i_{X} (X ∖ A)} : X ∖ A \to q_{f} \circ i_{X} (X ∖ A)$ は全単射連続写像であり $i_{X} | (X ∖ A) : X ∖ A \to Y ⨿ X$ は開写像であるから， $q_{f} | i_{X} (X ∖ A)$ が開写像であることを示せばよい．そこで $U \in τ (i_{X} (X ∖ A))$ とすると， $q_{f}^{- 1} (q_{f} (U)) = U$ より $q_{f} (U) \in τ (Y \cup_{f} X)$ を得る．
同値関係の定義より明らか．

閉部分空間の接着空間

閉集合 $X_{1} \in τ^{c} (X), Y_{1} \in τ^{c} (Y)$ が $f (X_{1} \cap A) \subset Y_{1}$ を満たすとする．このとき， $f_{1} := f |_{X_{1} \cap A}^{Y_{1}} : X_{1} \cap A \to Y_{1}$ による接着空間 $Y_{1} \cup_{f_{1}} X_{1}$ は $Y \cup_{f} X$ の閉部分空間と同相である．

商空間 $Y_{1} \cup_{f_{1}} X_{1}$ の普遍性より，単射連続写像 $\overset{―}{g} : Y_{1} \cup_{f_{1}} X_{1} \to Y \cup_{f} X$ であって $\overset{―}{g} \circ q_{f_{1}} = q_{f} \circ {id}_{Y_{1} ⨿ X_{1}}^{Y ⨿ X}$ を満たすものがただ一つ存在する．
$Y_{1} ⨿ X_{1} {id}_{Y_{1} ⨿ X_{1}}^{Y ⨿ X} q_{f_{1}} Y ⨿ X q_{f} Y_{1} \cup_{f_{1}} X_{1} \overset{―}{g} Y \cup_{f} X$
あとは $\overset{―}{g}$ が閉写像であることを示せばよい（定理2.7の系）．そのためには任意の $q_{f_{1}}$ 飽和閉集合 $C_{1} \subset Y_{1} ⨿ X_{1}$ に対して $q_{f} ({id}_{Y_{1} ⨿ X_{1}}^{Y ⨿ X} (C_{1})) \in τ^{c} (Y \cup_{f} X)$ が成り立つことを示せばよい（命題3.6）．そこで $C_{1} \subset Y_{1} ⨿ X_{1}$ を $q_{f_{1}}$ 飽和閉集合とする．このとき $i_{X_{1}}^{- 1} (C_{1}) \in τ^{c} (X_{1})$ および $q_{f_{1}} (C_{1}) \in τ^{c} (Y_{1} \cup_{f_{1}} X_{1})$ が成り立つので，命題10より
$i_{Y_{1}}^{- 1} (C_{1}) \cup f_{1} (i_{X_{1}}^{- 1} (C_{1}) \cap A) \in τ^{c} (Y_{1})$
を得る．ところで
$\begin{aligned} i_{X}^{- 1} ({id}_{Y_{1} ⨿ X_{1}}^{Y ⨿ X} & (C_{1})) = i_{X_{1}}^{- 1} (C_{1}) \in τ^{c} (X), \\ i_{Y}^{- 1} (j (C_{1})) \cup f (i_{X}^{- 1} & ({id}_{Y_{1} ⨿ X_{1}}^{Y ⨿ X} (C_{1})) \cap A) \\ = i_{Y_{1}}^{- 1} (C_{1}) \cup f_{1} (i_{X_{1}}^{- 1} (C_{1}) \cap A) \in τ^{c} (Y_{1}) \subset τ^{c} (Y) \end{aligned}$
が成り立つので，再び命題10より $q_{f} ({id}_{Y_{1} ⨿ X_{1}}^{Y ⨿ X} (C_{1})) \in τ^{c} (Y \cup_{f} X)$ を得る．

命題13の

$X$ を位相空間とし， $X_{1} \subset X$ をその閉集合とする．このとき，包含写像 ${id}_{X_{1}}^{X} : X_{1} \to X$ は $X_{1} / (X_{1} \cap A)$ から $X / A$ の閉部分空間への同相写像を誘導する．

命題13を $Y = Y_{1} = {*}, f = c : A \to {*}$ に対して適用すればよい．

接着空間の正規性

$X, Y$ が $T_{4}$ 空間ならば， $Y \cup_{f} X$ も $T_{4}$ 空間である．

$X, Y$ の $T_{1}$ 性より，任意の $y \in Y, a \in A, x \in X ∖ A$ に対して
$\begin{aligned} q_{f}^{- 1} (q_{f} (i_{Y} (y))) & = i_{Y} ({y}) \cup i_{X} (f^{- 1} ({y})), \\ q_{f}^{- 1} (q_{f} (i_{X} (a))) & = i_{X} (f^{- 1} ({f (a)})), \\ q_{f}^{- 1} (q_{f} (i_{X} (x))) & = i_{X} ({x}) \end{aligned}$
はいづれも $Y ⨿ X$ の閉集合であるから， $Y \cup_{f} X$ は $T_{1}$ 空間である．
$C_{1}, C_{2} \subset Y \cup_{f} X$ を交わらない閉集合とする．
- $F_{i} := i_{Y}^{- 1} (q_{f}^{- 1} (C_{i})) \subset Y$ は交わらない閉集合であるから， $Y$ の正規性より， $V_{i} \in τ (F_{i}, Y)$ であって $\overset{―}{V_{1}} \cap \overset{―}{V_{2}} = \emptyset$ となるものが存在する（命題2.28）．
- 命題12より $q_{f} \circ i_{Y} (\overset{―}{V_{i}}) \in τ^{c} (Y \cup_{f} X)$ であるから， $F_{i}^{'} := i_{X}^{- 1} (q_{f}^{- 1} (C_{i} \cup q_{f} \circ i_{Y} (\overset{―}{V_{i}}))) \in τ^{c} (X)$ となる．交わらない閉集合 $F_{1}^{'}, F_{2}^{'} \subset X$ に対して， $X$ の正規性より， $U_{i} \in τ (F_{i}^{'}, X)$ であって $U_{1} \cap U_{2} = \emptyset$ となるものが存在する．
- $W_{i} = q_{f} (i_{Y} (V_{i}) \cup i_{X} (U_{i} ∖ A))$ とおく．明らかに $W_{1} \cap W_{2} = \emptyset$ であり，
  $f (({id}_{A}^{X})^{- 1} (i_{X}^{- 1} (q_{f}^{- 1} (C_{i})))) \subset i_{Y}^{- 1} (q_{f}^{- 1} (C_{i})) \subset V_{i}$
  より
  $C_{i} \subset q_{f} (i_{Y} (F_{i}) \cup i_{X} (F_{i}^{'} ∖ A)) \subset q_{f} (i_{Y} (V_{i}) \cup i_{X} (U_{i} ∖ A)) = W_{i}$
  が成り立つ．あとは $W_{i} \in τ (Y \cup_{f} X)$ を示せばよい．
- 補題9より
  $\begin{aligned} i_{Y}^{- 1} (q_{f}^{- 1} (W_{i})) & = i_{Y}^{- 1} (i_{Y} (V_{i}) \cup i_{X} (U_{i} ∖ A)) \cup f (i_{X}^{- 1} (i_{Y} (V_{i}) \cup i_{X} (U_{i} ∖ A)) \cap A) \\ = V_{i} \in τ (Y) \end{aligned}$
  および
  $\begin{aligned} i_{X}^{- 1} (q_{f}^{- 1} (W_{i})) & = i_{X}^{- 1} (i_{Y} (V_{i}) \cup i_{X} (U_{i} ∖ A)) \cup f^{- 1} (i_{Y}^{- 1} (q_{f}^{- 1} (W_{i}))) \\ = (U_{i} ∖ A) \cup f^{- 1} (V_{i}) \end{aligned}$
  が成り立つので，あとは
  $(U_{i} ∖ A) \cup f^{- 1} (V_{i}) \in τ (X)$
  を示せばよい．
- $i_{X}^{- 1} (q_{f}^{- 1} (q_{f} \circ i_{Y} (V_{i}))) \subset F_{i}^{'} \subset U_{i}$ より
  $q_{f} \circ i_{X} \circ {id}_{A}^{X} (f^{- 1} (V_{i})) = q_{f} \circ i_{Y} \circ f (f^{- 1} (V_{i})) \subset q_{f} \circ i_{Y} (V_{i})$
  となるので， $f^{- 1} (V_{i}) \subset U_{i}$ が成り立つ．
- また， $f^{- 1} (V_{i}) \in τ (A)$ より $U_{i}^{'} \in τ (X)$ であって $f^{- 1} (V_{i}) = U_{i}^{'} \cap A$ となるものが存在する．
- よって
  $(U_{i} ∖ A) \cup f^{- 1} (V_{i}) = (U_{i} ∖ A) \cup (U_{i} \cap U_{i}^{'} \cap A) = (U_{i} ∖ A) \cup (U_{i} \cap U_{i}^{'}) \in τ (X)$
  が成り立つ．

命題14の

$X$ が $T_{4}$ 空間ならば $X / A$ も $T_{4}$ 空間である．

位相空間の貼り合わせ

包含写像による部分空間の貼り合わせ

$X$ を位相空間とし $(A, B)$ をその開被覆（resp. 閉被覆）とする．このとき $X$ と $A \cup_{A \cap B} B$ とは同相である．

商写像を $q : A ⨿ B \to A \cup_{A \cap B} B$ とおく．連続写像

$f_{A} := q \circ i_{A} : A \to A \cup_{A \cap B} B$
$f_{B} := q \circ i_{B} : B \to A \cup_{A \cap B} B$

について $f_{A} | A \cap B = f_{B} | A \cap B$ が成り立つ．命題4.9より $(A, B)$ は $τ (X)$ と整合的な被覆であるから，命題 $4.5$ より連続写像 $f : X \to A \cup_{A \cap B} B$ が定まる．一方，包含写像について
${id}_{A}^{X} \circ {id}_{A \cap B}^{A} = {id}_{A \cap B}^{X} = {id}_{B}^{X} \circ {id}_{A \cap B}^{B}$
が成り立つので，接着空間の普遍性より，連続写像 $g : A \cup_{A \cap B} B \to X$ が定まる．
$A \cap B {id}_{A \cap B}^{B} {id}_{A \cap B}^{A} B q \circ i_{B} {id}_{B}^{X} A q \circ i_{A} {id}_{A}^{X} A \cup_{A \cap B} B g X$
こうして定まる $f, g$ が互いの逆写像であることは明らかであろう．

$(A, B)$ が開被覆でなくても， $(int (A), int (B))$ が被覆になっていれば十分である（cf. 命題4.9）．

附：コサイクルによる位相空間族の貼り合わせ

$X = ((X_{λ}, τ_{λ}))_{λ \in Λ}$ を位相空間族とする．また，各 $(λ, μ) \in Λ \times Λ$ に対して，

開集合 $A_{λ}^{μ} \subset X_{λ}$ ，ただし $A_{λ}^{λ} = X_{λ}$ ;
同相写像 $f_{λ}^{μ} : A_{λ}^{μ} \to A_{μ}^{λ}$ ，ただし $f_{λ}^{λ} = {id}_{X_{λ}}$

が与えられているとする．族 $f = (f_{λ}^{μ} : A_{λ}^{μ} \to A_{μ}^{λ})_{(λ, μ) \in Λ \times Λ}$ がコサイクル条件
$\forall (λ, μ, ν) \in Λ \times Λ \times Λ, \forall x \in A_{λ}^{μ} \cap A_{λ}^{ν}, f_{λ}^{ν} (x) = f_{μ}^{ν} \circ f_{λ}^{μ} (x)$
を満たすとき， $f$ を $X$ 上のコサイクルという（ことにする）．

$f$ を $X$ 上のコサイクルとする．余積空間 $\tilde{X} := \underset{λ \in Λ}{∐} X_{λ}$ 上の関係
$R (f) := {(\tilde{x}, {\tilde{x}}^{'}) \in \tilde{X} \times \tilde{X} ∣ \exists λ, μ \in Λ, \tilde{x} \in A_{λ}^{μ}, {\tilde{x}}^{'} \in A_{μ}^{λ}, f_{λ}^{μ} (\tilde{x}) = {\tilde{x}}^{'}}$
は同値関係である．ただし位相的埋め込み $i_{λ} : X_{λ} \to ∐ X_{∙}$ により $X_{λ} \subset \tilde{X}$ と見做している．

$\tilde{x} \in \tilde{X}$ とする．このとき $λ \in Λ$ であって $\tilde{x} \in X_{λ}$ となるものが存在するので $f_{λ}^{λ} (\tilde{x}) = \tilde{x}$ が成り立つ．したがって $(\tilde{x}, \tilde{x}) \in R (f)$ を得る．
$(\tilde{x}, {\tilde{x}}^{'}) \in R (f)$ とする．このとき， $λ, μ \in Λ$ であって
$\tilde{x} \in A_{λ}^{μ}, {\tilde{x}}^{'} \in A_{μ}^{λ}, f_{λ}^{μ} (\tilde{x}) = {\tilde{x}}^{'}$
となるものが存在する．コサイクル条件において $ν = λ$ とすることで $f_{μ}^{λ} \circ f_{λ}^{μ} = {id}_{A_{λ}^{μ}}$ となることがわかるので，
${\tilde{x}}^{'} \in A_{μ}^{λ}, \tilde{x} \in A_{λ}^{μ}, f_{μ}^{λ} ({\tilde{x}}^{'}) = \tilde{x}$
すなわち $({\tilde{x}}^{'}, \tilde{x}) \in R (f)$ が成り立つ．
$(\tilde{x}, {\tilde{x}}^{'}), ({\tilde{x}}^{'}, {\tilde{x}}^{″}) \in R (f)$ とする．このとき， $λ, μ, ν \in Λ$ であって
$\tilde{x} \in A_{λ}^{μ}, {\tilde{x}}^{'} = f_{λ}^{μ} (\tilde{x}) \in A_{μ}^{λ} \cap A_{μ}^{ν}, {\tilde{x}}^{″} = f_{μ}^{ν} ({\tilde{x}}^{'}) \in A_{ν}^{μ}$
となるものが存在する．したがって
${\tilde{x}}^{″} = f_{μ}^{ν} ({\tilde{x}}^{'}) = f_{λ}^{ν} \circ f_{μ}^{λ} ({\tilde{x}}^{'}) = f_{λ}^{ν} (\tilde{x}) \in A_{ν}^{λ}$
が成り立つので，
$\tilde{x} \in f_{ν}^{λ} (A_{ν}^{λ}) = A_{λ}^{ν}, {\tilde{x}}^{″} \in A_{ν}^{λ}, f_{λ}^{ν} (\tilde{x}) = {\tilde{x}}^{″}$
すなわち $(\tilde{x}, {\tilde{x}}^{″}) \in R (f)$ を得る．

$f$ を $X$ 上のコサイクルとし， $X = \tilde{X} / R (f)$ とおく．また，各 $λ \in Λ$ に対して $q_{λ} = q_{R (f)} | X_{λ} : X_{λ} \to X$ とおく．このとき
$(q_{λ})^{q_{λ} (X_{λ})} : X_{λ} \approx q_{λ} (X_{λ}) \in τ (X)$
が成り立つ．とくに

$(q_{λ} (X_{λ}))_{λ \in Λ}$ は $X$ の開被覆であり，したがって
位相空間 $Y$ への写像 $f : X \to Y$ が連続であるためには，任意の $λ \in Λ$ に対して $f | q_{λ} (X_{λ})$ が連続であることが必要かつ十分である．

$q_{λ}$ が単射連続開写像であることを示せばよい（定理2.7の系）．

連続性は明らか．
$x, x^{'} \in X_{λ}, q_{λ} (x) = q_{λ} (x^{'})$ とする．このとき， $x, x^{'} \in X_{λ}, (x, x^{'}) \in R (f)$ より $x^{'} = f_{λ}^{λ} (x) = x$ が成り立つ．
$U \in τ (X_{λ})$ とする．このとき任意の $μ \in Λ$ に対して， $q_{λ} \circ f_{μ}^{λ} = q_{μ} | A_{μ}^{λ}$ および
$\begin{aligned} U \cap A_{λ}^{μ} & = U \cap q_{λ}^{- 1} (q_{λ} (X_{λ}) \cap q_{μ} (X_{μ})) \\ = q_{λ}^{- 1} (q_{λ} (U) \cap q_{λ} (X_{λ}) \cap q_{μ} (X_{μ})) \\ = q_{λ}^{- 1} (q_{λ} (U) \cap q_{μ} (X_{μ})) \end{aligned}$
より
$q_{R (f)}^{- 1} (q_{λ} (U)) \cap X_{μ} = q_{μ}^{- 1} (q_{λ} (U) \cap q_{μ} (X_{μ})) = f_{λ}^{μ} (U \cap A_{λ}^{μ}) \in τ (X_{μ})$
が成り立つ． $(X_{μ})_{μ \in Λ}$ は $\tilde{X}$ の開被覆であるから， $q_{R (f)}^{- 1} (q_{λ} (U)) \in τ (\tilde{X})$ を得る．よって $q_{λ} (U) \in τ (X)$ が成り立つ．

$B$ を位相空間， $U = (U_{λ})_{λ \in Λ}$ を $B$ の開被覆とし， $G$ を位相群とする．連続写像族 $g = (g_{λ}^{μ} : U_{λ} \cap U_{μ} \to G)_{(λ, μ) \in Λ \times Λ}$ がコサイクル条件
$\forall (λ, μ, ν) \in Λ \times Λ \times Λ, \forall x \in U_{λ} \cap U_{μ} \cap U_{ν}, g_{λ}^{ν} (x) = g_{μ}^{ν} (x) \cdot g_{λ}^{μ} (x)$
を満たすとき， $g$ を $G$ 値 $U$ コサイクルという（ことにする）．

$g_{λ}^{λ} (x) = g_{λ}^{λ} (x) \cdot g_{λ}^{λ} (x)$ より， $g_{λ}^{λ} (x) = e_{G}$ が成り立つ；
前段より， $g_{μ}^{λ} (x) \cdot g_{λ}^{μ} (x) = g_{λ}^{λ} (x) = e_{G}$ が成り立つ．

$B$ を位相空間， $U = (U_{λ})_{λ \in Λ}$ を $B$ の開被覆， $G$ を位相群， $g$ を $G$ 値 $U$ コサイクルとする．また， $F$ を位相空間とし， $G \times F \to F$ を（効果的な）連続作用とする．このとき，

$X_{λ} = U_{λ} \times F$ ;
$A_{λ}^{μ} = (U_{λ} \cap U_{μ}) \times F$ ;
$f_{λ}^{μ} : A_{λ}^{μ} \to A_{μ}^{λ}; (b, y) \mapsto (b, g_{λ}^{μ} (b) \cdot y)$

と定めると， $f = (f_{λ}^{μ})_{(λ, μ) \in Λ \times Λ}$ は $(X_{λ})_{λ \in Λ}$ 上のコサイクルとなる．そこで

$\tilde{E} = ∐ X_{∙}$ ;
$E = \tilde{E} / R (f)$ ;
$π : E \to B; [λ, b, y] \mapsto b$

と定めると， $π$ は（ $G$ を構造群とする） $F$ 束の構造を持つ．

$q : \tilde{E} \to E$ を商写像とする．

射影

各 $λ \in Λ$ に対して
$p_{λ} = {id}_{U_{λ}}^{B} \circ p_{U_{λ}} : X_{λ} \to U_{λ} \subset B$
とおくと，連続写像族 $(p_{λ})_{λ \in Λ}$ は連続写像 $∐ p_{∙} : \tilde{E} \to B$ を誘導する．また，
$(\tilde{e}, {\tilde{e}}^{'}) \in R (f) ⟹ (∐ p_{∙}) (\tilde{e}) = (∐ p_{∙}) ({\tilde{e}}^{'})$
が成り立つので，商空間の普遍性より連続写像 $π : E \to B$ が誘導される．
$\tilde{E} ∐ p_{∙} q B E π$

局所自明化

$b \in B$ とする．このとき $λ \in Λ$ であって $b \in U_{λ}$ となるものが存在する．そこで，同相写像 $(q_{λ})^{q (X_{λ})} : X_{λ} \to q (X_{λ}) = π^{- 1} (U_{λ})$ の逆写像を局所自明化
$φ_{λ} : π^{- 1} (U_{λ}) \to X_{λ} = U_{λ} \times F$
として取ればよい．これは $π^{- 1} (U_{λ}) \cap π^{- 1} (U_{μ})$ 上で
$φ_{λ} ([μ, b, y]) = (b, g_{μ}^{λ} (b) \cdot y)$
によって与えられる写像である．

変換函数

任意の $λ, μ \in Λ$ と $(b, y) \in (U_{λ} \cap U_{μ}) \times F$ とに対して
$φ_{λ} \circ φ_{μ}^{- 1} (b, y) = (b, g_{μ}^{λ} (b) \cdot y)$
が成り立つ．

参考文献

[1]

N. Bourbaki, General Topology Chapters 1--4

[2]

J. Dugundji, Topology

[3]

小松醇郎，中岡稔，菅原正博, 『位相幾何学 I』, 岩波書店

投稿日：2023年10月29日

更新日：2024年10月14日

この本を高評価した人

高評価したユーザはいません

この本に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

うすい

12045

位相空間論に興味があります．

他の人のコメント

コメントはありません。

読み込み中

うすい

New Spaces from Old

現在のページ

商空間

商空間
部分集合を一点につぶして得られる空間
接着空間
位相空間の貼り合わせ
包含写像による部分空間の貼り合わせ
附：コサイクルによる位相空間族の貼り合わせ
参考文献

前のページへ

5 / 7

次のページへ

前ページへ

次ページへ

商空間

商空間