2025年5月3日~5月11日にかけて『
第5回匿式図形問題エスパー杯
(T-GUESS Cup 5: Tock's Geometry "Using Extra-Sensory Solutions" Cup The 5th)』を開催しました。ご参加くださった皆様、ありがとうございました。
本記事では、当該コンテストで出題した問題A・問題B・問題C・問題D・問題Eの紹介および解説を行います。昨年度同様、最終問題である問題Fは別記事にて解説することといたします。
T-GUESS Cup 2の解説記事:
問題A~C
・
問題D
T-GUESS Cup 3の解説動画:
問題A~H
T-GUESS Cup 4の解説記事:
問題A~E
・
問題F
問題紹介
対角線が直交する四角形が円に内接しています。のとき、で囲まれる領域の面積を求めてください。ただし、円周率はとします。
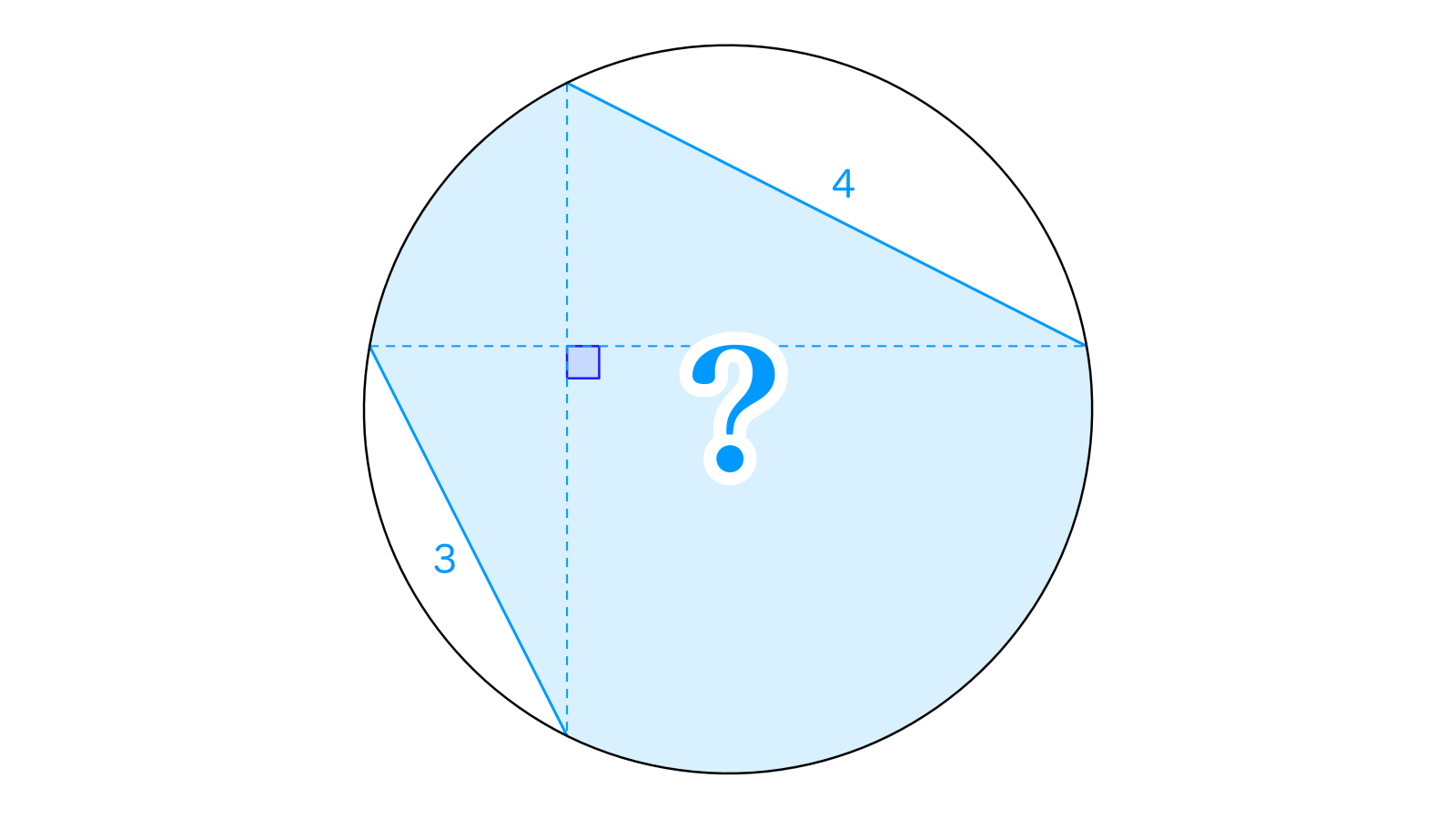
(問題B)
1辺の長さがである正方形において、の延長上にそれぞれ点を、となるようにとります。が成立するとき、の面積を求めてください。
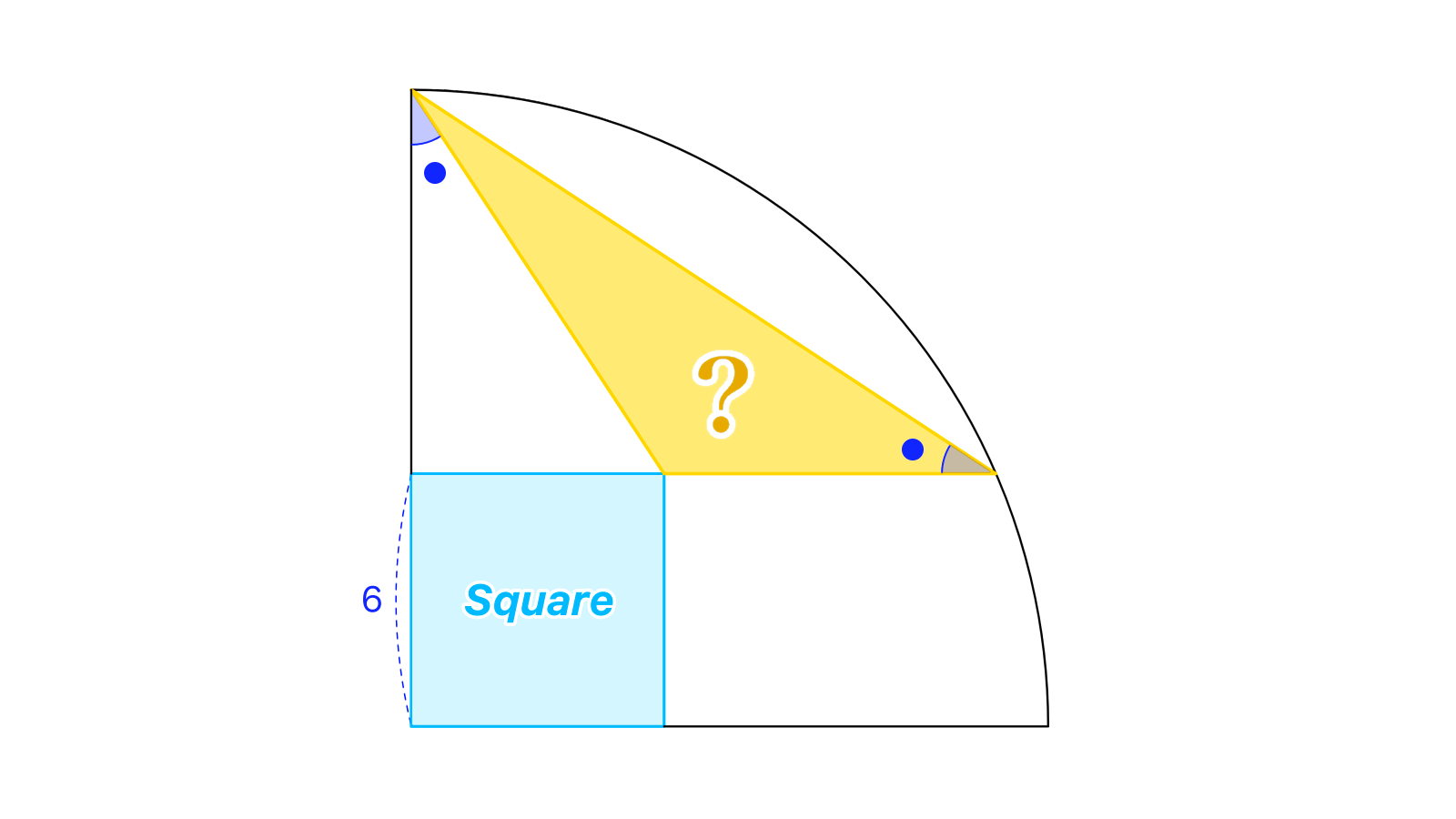
正方形の内部に点をとり、直線上に2点をとると、四角形はいずれも円に内接しました。のとき、正方形の1辺の長さを求めてください。
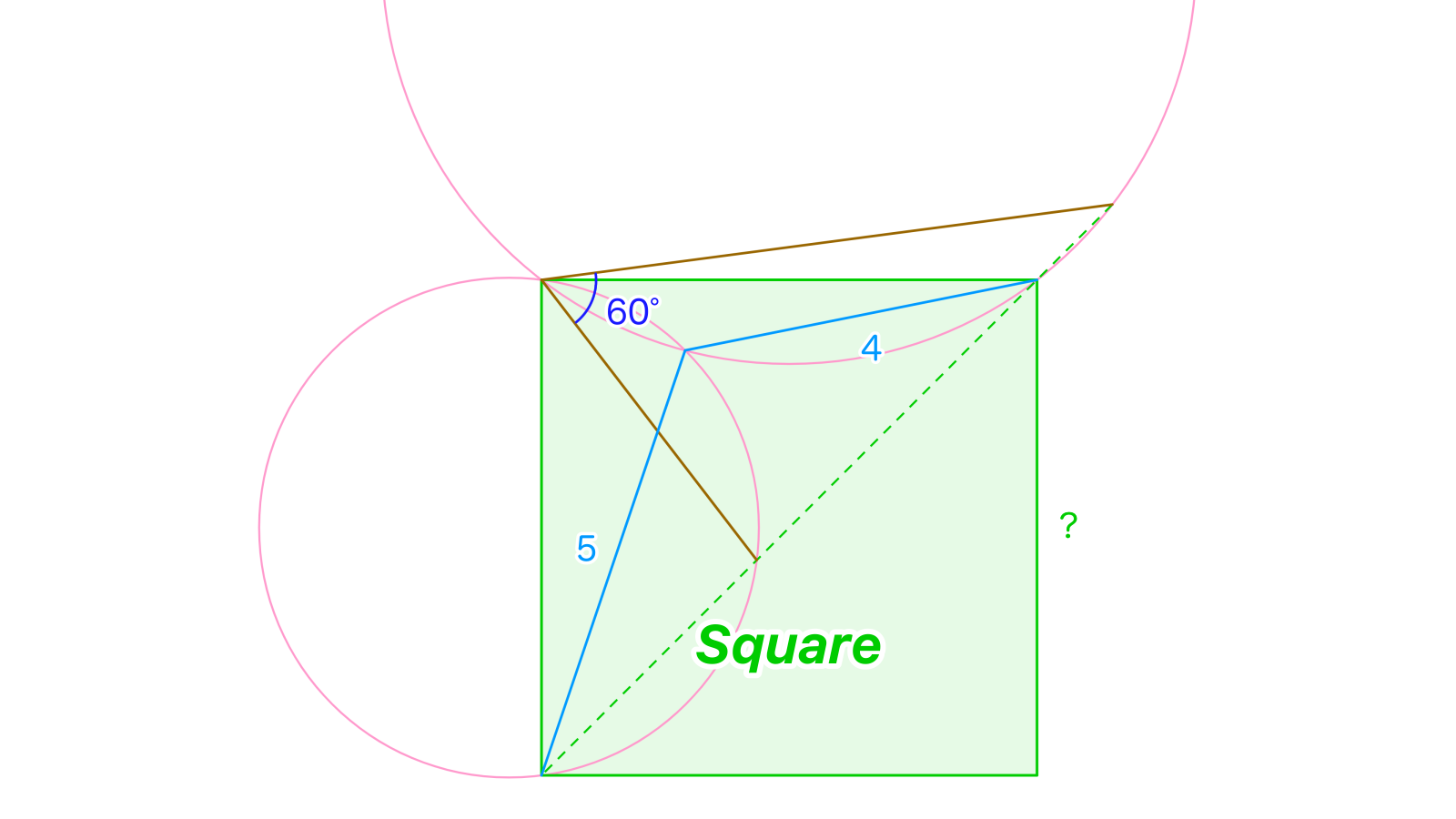
(問題D)
3つの円があり、とは2点で、とは2点で、とは2点で、それぞれ交わっています。いま、とは直交し、その交点は点に一致しました。直線に関し点がある側の領域をとし、の面積がそれぞれであるとき、の面積を求めてください。
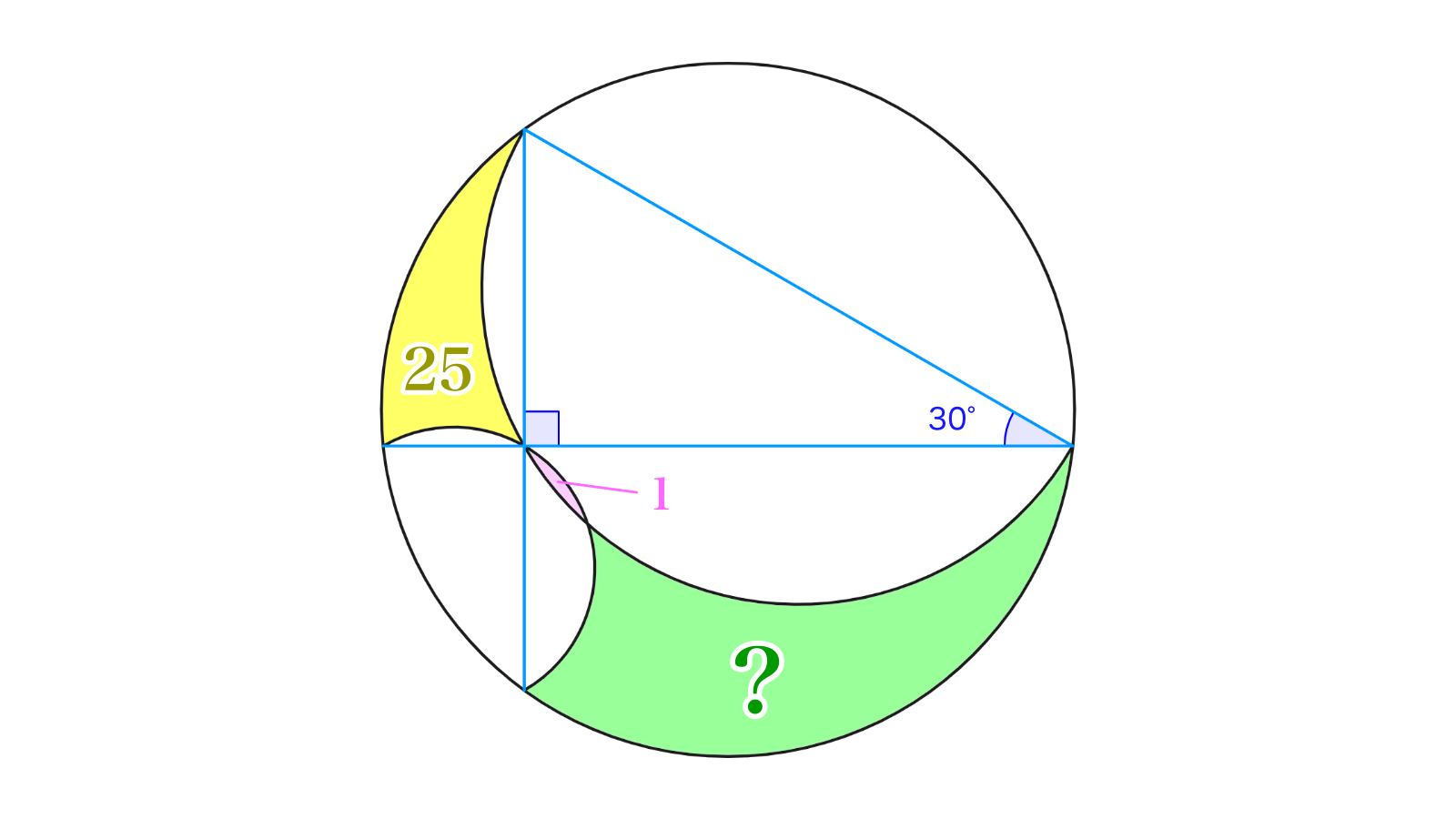
(問題E)
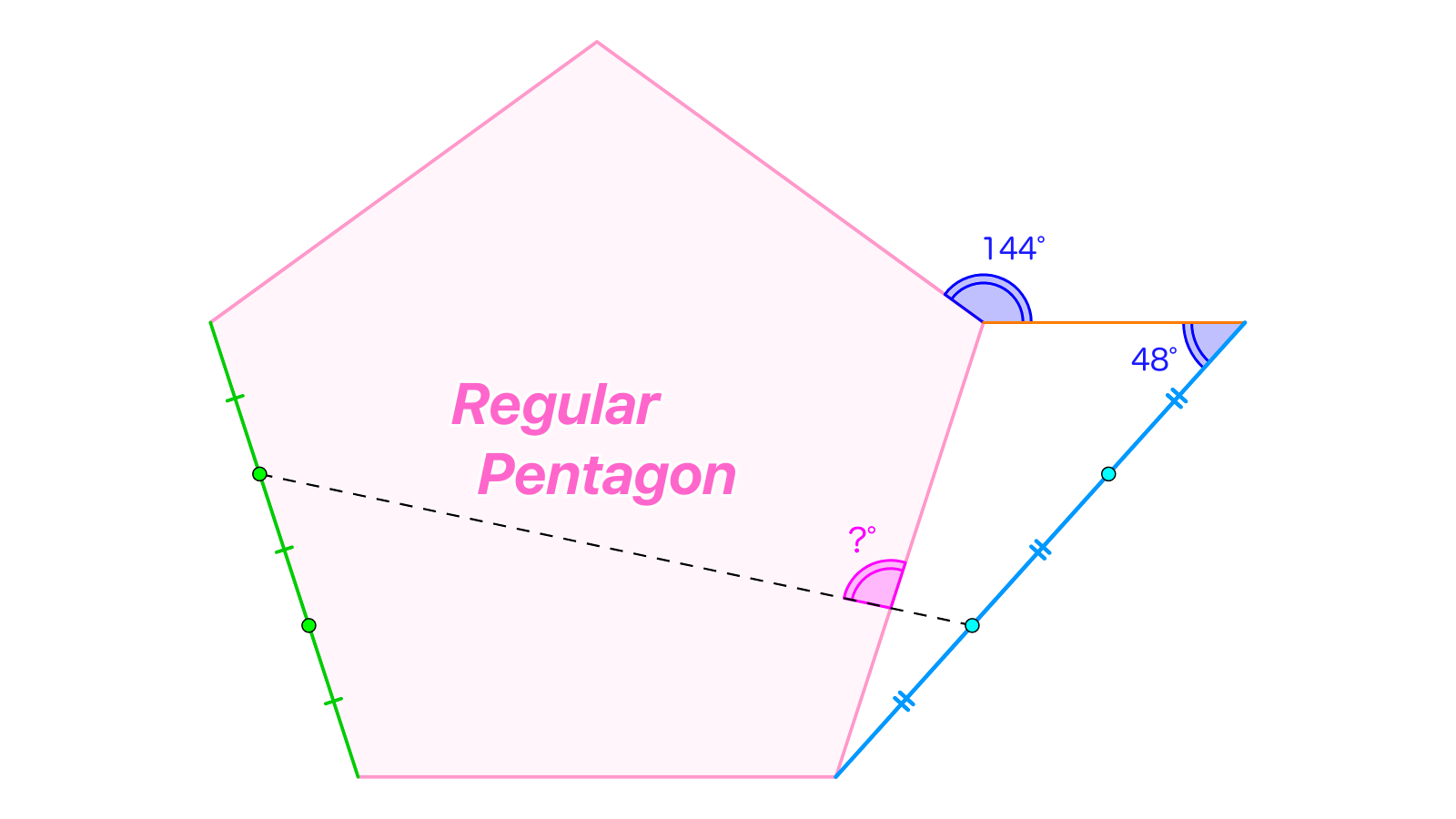
正五角形の外部にとなる点をとります。線分上にとなる点 を、線分上にとなる点 をそれぞれとり、との交点をとしたとき、の大きさを求めてください。
解答発表
問題A
問題B
問題C
問題D
問題E
軽い解説
問題A
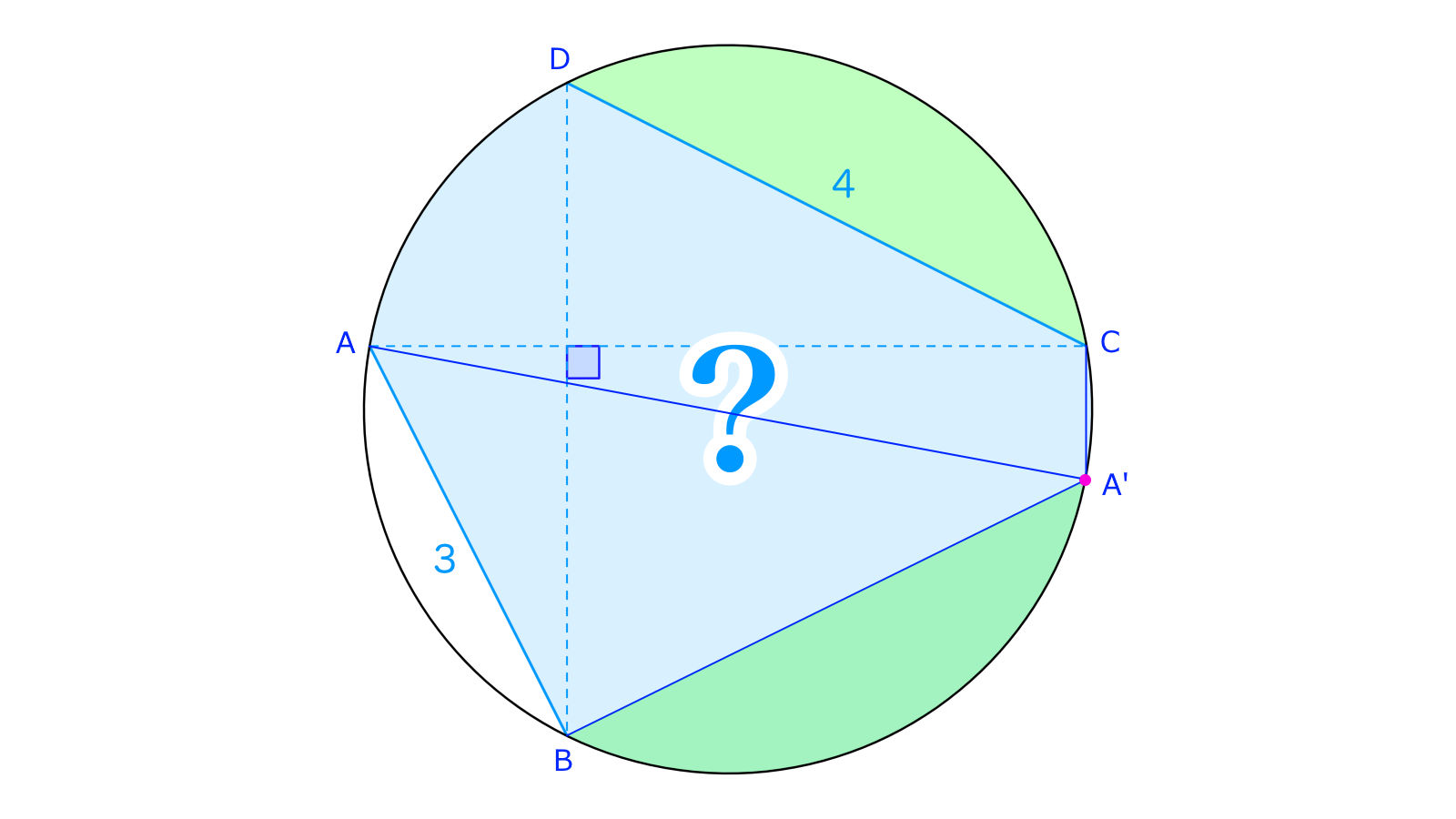
線分が円の直径となるような点をとると、円周角の定理(もしくはタレスの定理)よりです。したがってであり、との長さは等しくなります。ある円における弧の長さが等しければ弦の長さも等しいため、となり、三平方の定理を用いてが判ります。
また、で囲まれた領域をで囲まれた領域に移動させることができるので、求める面積はもとの円の半分にをくっつけた領域のそれです。半円の面積は、の面積はと計算でき、結局本問の答えはとなります。
問題B
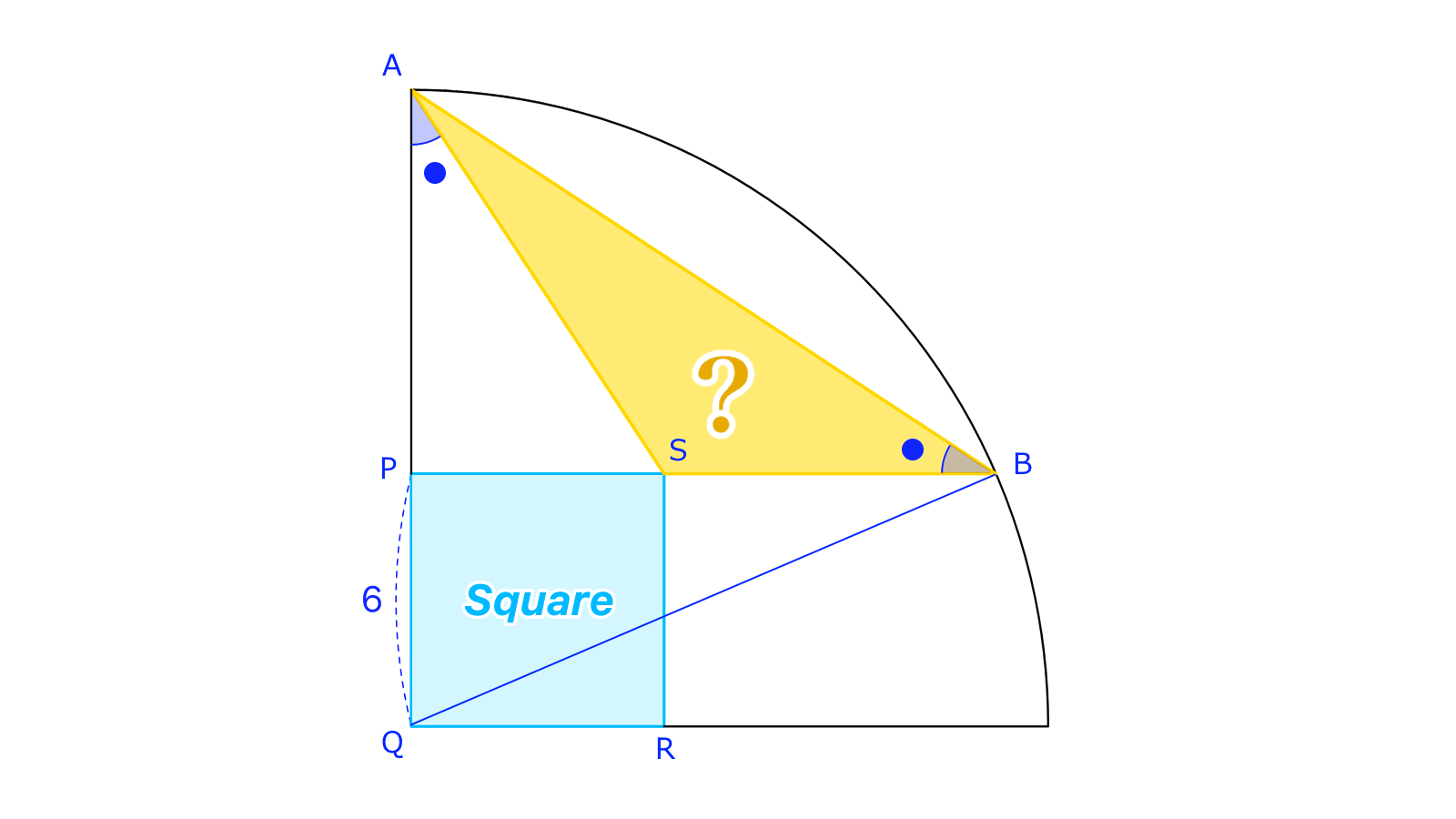
とおきます。とに注目すれば、2つの角がそれぞれ等しいのでこれらの三角形は相似です。ゆえにとなり、よりが得られます。
いま、で三平方の定理を用いると、
となり、と求められ……なくもありませんが、ここではの厳密な値を求めなくてよいです。なぜならば、
と計算できて、の値さえ分かれば答えを出せるからです。つまり、本問の答えはとなります。
別解(天真 氏より)
直線に関し点と対称な点をそれぞれとすると、点は四分円を延長した円周上に存在します。円周角の定理からが判るため、は、2つの角がそれぞれ等しいのですべて相似といえます(どの2つの角を用いるかは三角形の組により異なります)。よってであり、3点は同一直線上に存在するのですね。より、すなわちと導けて、特に求めるべき面積はとなります。エレガント。
問題C
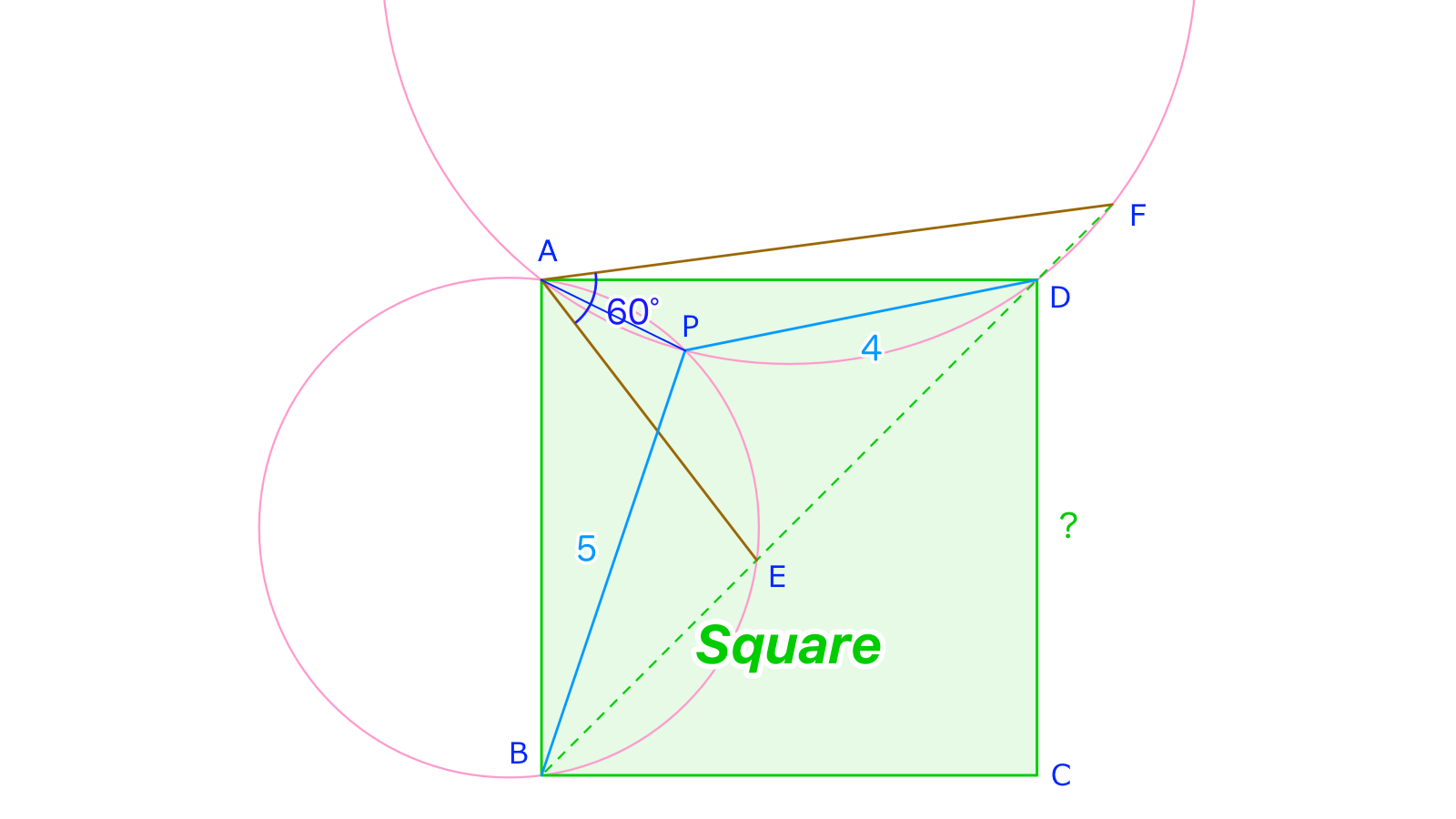
問題A・問題Bよりも条件が多く戸惑いますが、「の長さを求められそう」という直感が大事です。
とし、円に注目すればとなります。このときなので、円に注目しても判ります。ゆえに、の内角を考え、が得られます。あとは単なる余弦定理で済み、、すなわち本問の答えはです。Bより簡単では?
問題D
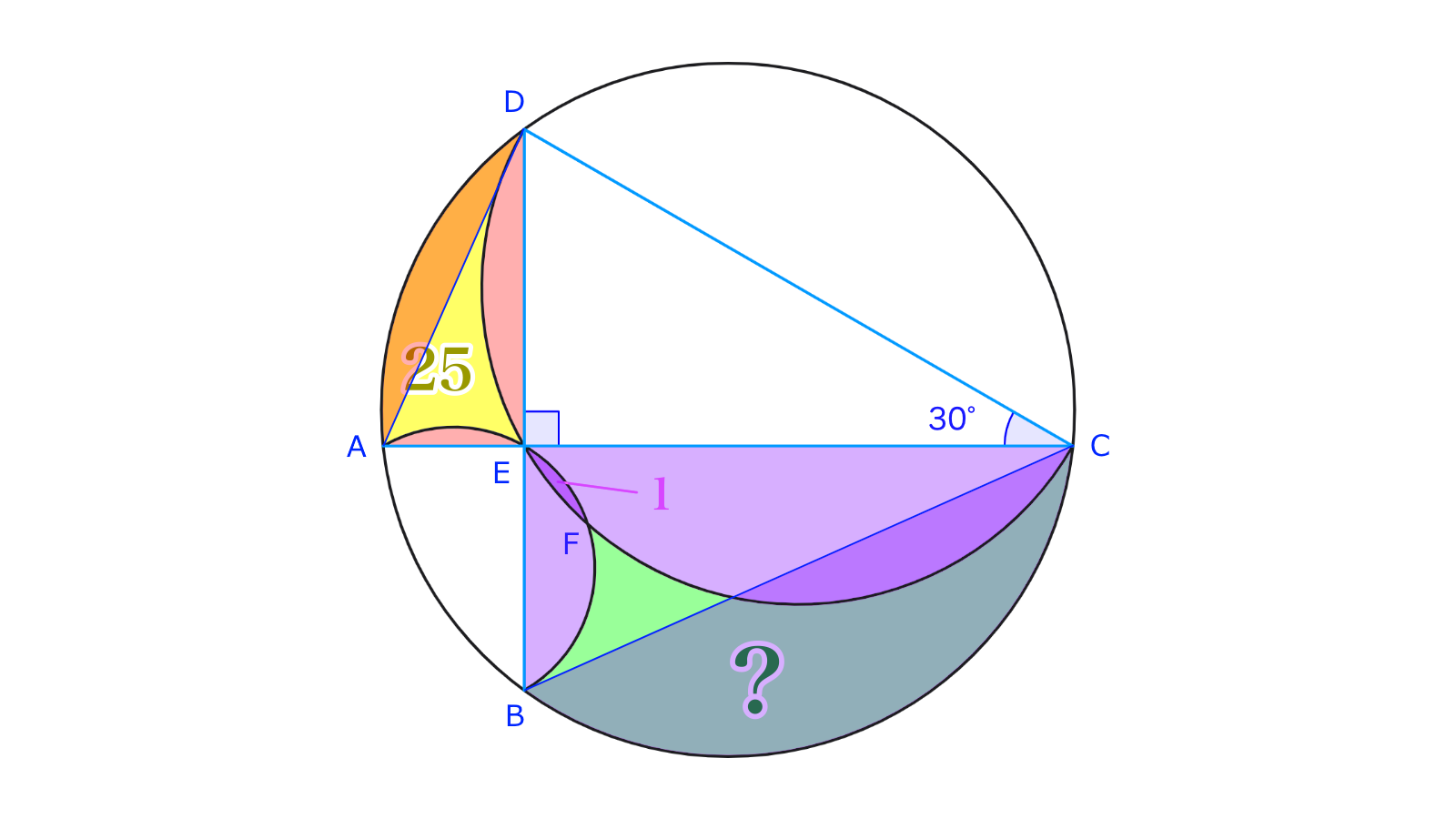
で、円における劣弧を表すこととします(独自表記です)。に対する円周角を考えると、これらはすべてです。したがって、これらはいずれも円周のに相当し、で囲まれる領域、で囲まれる領域、で囲まれる領域(それぞれとします)は相似であるといえます。相似比はに等しく、三平方の定理よりですから、面積についてが成立します(相似比がのとき、面積比はです)。からを除き、とをくっつければになるため、が判明します。
の面積(求める面積)をとおき、で囲まれる領域、で囲まれる領域、で囲まれる領域をそれぞれとします。前段落の議論と同様にしてが判り、が従いますね(行間が広くないか?)。に気づくと、その相似比は明らかにですから、、ひいてはが確定します。一目瞭然ですが、
ヒポクラテスの三日月
を応用して作問しました。
問題E
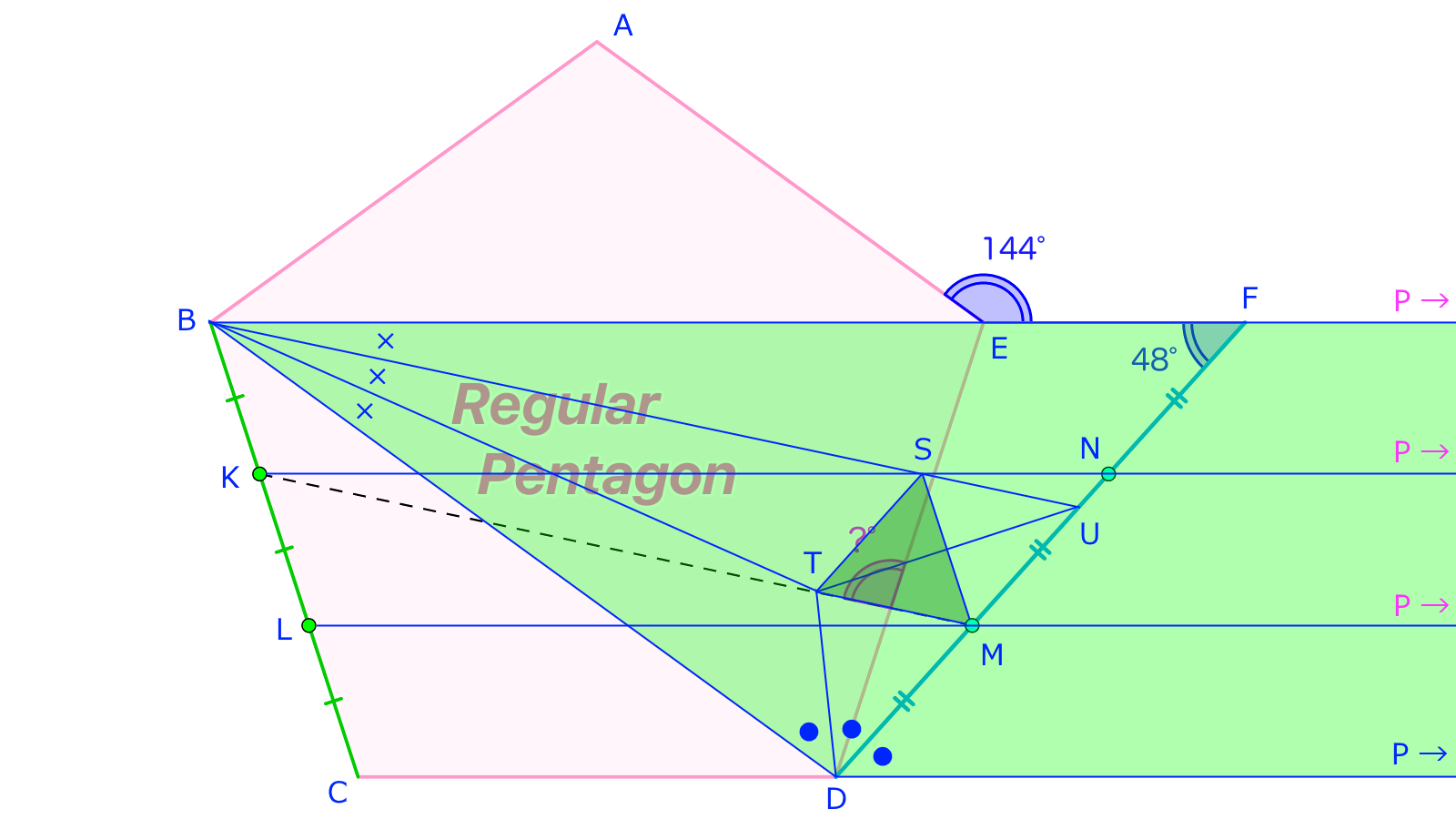
半直線上の無限遠点(限りなく遠くにある点)をとします。このとき、より、2直線は重なるとみなせるのです。よって、3直線はの3辺をそれぞれ含むと言えます。
いま、で
フランク・モーリーの定理
を用いてみましょう。なので、この角はずつ分ければよいです。また、なので、この角はずつ分ければよいです。はどうしましょうか。実は、三角形のある頂点を無限遠に飛ばしたとき、その頂点から引いた内角の三等分線は、その頂点が属する平行な2辺をちょうど三等分する平行線になるのです(すごく細長い三角形を考えるとイメージが掴めるかも)。
今回の場合、点は辺に属するため、直線がまさにその三等分線なのです。ということで、モーリーの三角形を拵えることができます(ただし、はをみたす線分上の点、はをみたす内の点)。
ここまで思いつけたらあと一息です。との交点をとすれば、の内心がに一致し、、すなわちも正三角形になります(ヒント:中心、半径の円でに対する円周角を考えます)。よってであり、またからも従います。ゆえに四角形は平行四辺形と判り、必然的に四角形も平行四辺形です(1組の対辺が平行かつ等長)。このことはを導き、直ちにと結論づけられます。三角関数の計算を頑張っても正答できますが、こう解いたほうが明らかにスタイリッシュですね。
次回予告
ここまでで5問の解説が済みました。あなたのお気に入りの問題はどれですか? えっ、ない? そう仰らずに……。
前回のA~E
と比べると、今回は結構大人しいですね。あとは問題Fを残すのみですが、はたしてこちらは大人しく解かれてくれるでしょうか。
(問題F)
九角形はおよびをみたします。のとき、の大きさを求めてください。
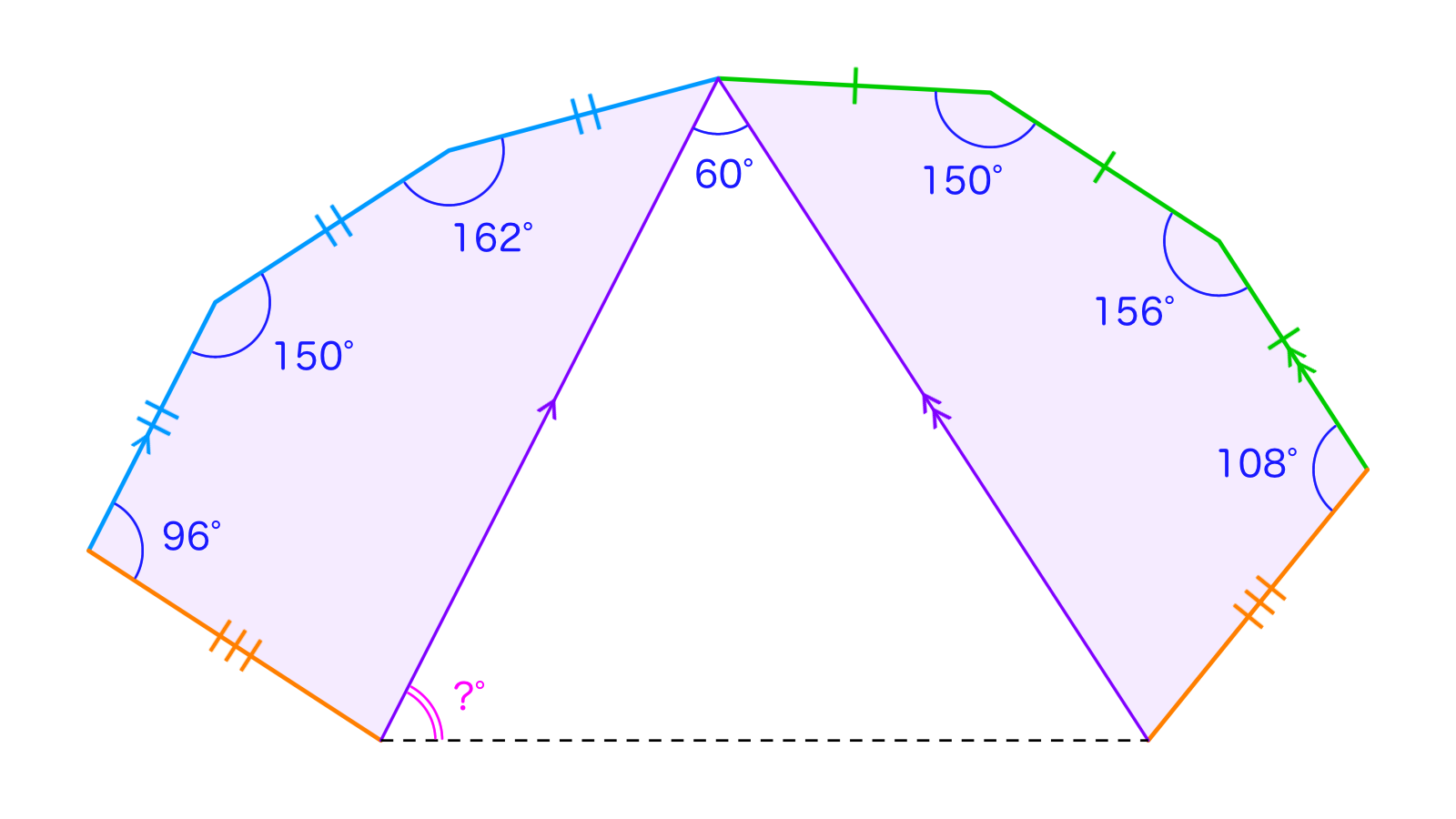
おや、今回はレムニスケートや三角形の五心で威圧する感じではなさそうです。とはいえ、よく分からない等辺や角度の情報が多く、GeoGebra等で作図してみても使えそうな性質がほぼ出てきません。毎度お馴染み「どうやってこの図形を見つけてきたんだ……?」タイムが訪れますね。お答えしましょう。根性です。の超低品質プログラムを組み、ノートパソコン様に十数時間頑張ってもらいました。本当にありがとうマイラップトップ。
次回、この問題Fを解き、さらに若干の一般化を与えます。昨年ほどの暴走は控えるつもりですが、何卒ご期待くださいませ。
ご感想・ご指摘・巧妙な解法・コンテスト広報活動のコツなどがございましたら、是非ともコメントに残していってください。ここまでお読みいただき、ありがとうございました。











