Fibonacci 数を含む基礎的な無限級数 (3) F_(n+k) F_n の逆数和
 20210105
20210105
前提知識 : Lucas 数列, Fibonacci 数列
Lucas 数列, Fibonacci 数列 :
https://mathlog.info/articles/191
(1) の記事 :
https://mathlog.info/articles/1468
(2) の記事 :
https://mathlog.info/articles/1469
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
最新版 :
https://yu200489144.hatenablog.com/entry/2021/01/05/232023
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
今回の記事では$F_{n+k}F_n$の逆数和を一般的に扱い, その具体的な計算手法を与える. これらの手法に由れば, 幾つかの単純な無限和は機械的に計算することができるように成るであろう.
$1/F_{n+2k}F_n$の無限和
任意の正の整数$k$に対して, 無限級数$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{n+k}F_n}$の収束値を$S_k$と置く.
$1/F_{n+2}F_n$の無限和を再掲する.
$S_2=1$が成りたつ.
$F_{n+1}=F_{n+2}-F_n$であることを用いれば
$$
\begin{align}
S_2&=\sum_{n\geqslant1}^n\frac{F_{n+2}-F_n}{F_{n+2}F_{n+1}F_n}\\
&=\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+1}F_n}-\frac{1}{F_{n+2}F_{n+1}}\right)\\
&=\frac{1}{F_1F_2}=1
\end{align}
$$と計算できる. $\quad\Box$
$S_4=\dfrac{7}{18}$が成りたつ.
$F_{n+4}=F_{n+3}+F_{n+2}=2F_{n+2}+F_{n+1}=3F_{n+2}-F_n$であること, および先の命題を用いれば
$$
\begin{align}
S_4&=\sum_{n\geqslant1}^n\frac{F_{n+4}-F_n}{3F_{n+4}F_{n+2}F_n}\\
&=\frac{1}{3}\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+2}F_n}+\frac{1}{F_{n+4}F_{n+2}}\right)\\
&=\frac{1}{3}\left(1+1-\frac{1}{F_1F_3}-\frac{1}{F_2F_4}\right)=\frac{7}{18}
\end{align}
$$と計算できる. $\quad\Box$
一般化を考えるために, 正整数$k$を任意に取って
$$
\begin{align}
F_{n+2k}=a_kF_{n+2}+b_kF_n
\end{align}
$$なる数列$(a_k)_{k>0},(b_k)_{k>0}$を構成する. $k$を固定すれば, $n=0$および$n=1$において成立していれば, 辺々を足しあわせるか, あるいは引く操作を繰りかえすことで一般の$n$についての等式の成立が判るので, 帰納的に$n\in\{0,1\}$として計算して構わない. 由って
$$
\begin{align}
\left(
\begin{array}{ll}
F_{2k}=a_k\\
F_{1+2k}=2a_k+b_k
\end{array}
\right.
\end{align}
$$なる連立方程式を解くのみであり,
$$
\begin{align}
&a_k=F_{2k}\\
&b_k=F_{2k+1}-2F_{2k}=F_{2k-1}-F_{2k}=-F_{2k-2}
\end{align}
$$が要求を充たす.
任意の正整数$k,n$に対して, $F_{n+2k}=F_{2k}F_{n+2}-F_{2k-2}F_n$が成りたつ.
$k$を固定して考える. $n\in\{0,1\}$のときに成立することは既知である. それぞれの等式について, ある$n+1,n$について等式が成りたつならば, それらを辺々足しあわせることで$n+2$の場合が得られ. また辺々を引けば$n-1$の場合が得られるので, 再帰的に命題は示された. $\quad\Box$
任意の$2$以上の整数$k$に対して, $S_{2k}=\displaystyle\frac{1}{F_{2k}}\sum_{n=1}^{n=k}\frac{1}{F_{2n}F_{2n-1}}$が成りたつ.
$F_{2k}F_{n+2}=F_{n+2k}+F_{2k-2}F_n$であることを用いて
$$
\begin{align}
S_{2k}&=\frac{1}{F_{2k}}\sum_{n\geqslant1}^n\frac{F_{n+2k}+F_{2k-2}F_n}{F_{n+2k}F_{n+2}F_n}\\
&=\frac{1}{F_{2k}}\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+2}F_n}+\frac{F_{2k-2}}{F_{n+2k}F_{n+2}}\right)\\
&=\frac{1}{F_{2k}}\left(1+F_{2k-2}\left(S_{2k-2}-\frac{1}{F_{2k-1}}-\frac{1}{F_{2k}}\right)\right)
\end{align}
$$と式変形し, 両辺に$F_{2k}$を掛けて右辺の括弧を展開すれば$\left(S_{2k}F_{2k}\right)_{k>0}$の漸化式が得られることが判る. 実際には
$$
\begin{align}
F_{2k}S_{2k}&=F_{2k-2}S_{2k-2}+1+F_{2k-2}\left(-\frac{1}{F_{2k-1}}-\frac{1}{F_{2k}}\right)\\
&=F_{2k-2}S_{2k-2}+\frac{F_{2k}F_{2k-1}-F_{2k}F_{2k-2}-F_{2k-1}F_{2k-2}}{F_{2k}F_{2k-1}}\\
&=F_{2k-2}S_{2k-2}+\frac{F_{2k-1}F_{2k-1}-F_{2k}F_{2k-2}}{F_{2k}F_{2k-1}}\\
&=F_{2k-2}S_{2k-2}+\frac{1}{F_{2k}F_{2k-1}}
\end{align}
$$と階差$1/F_{2k+2}F_{2k+1}$の数列になるため,
$$
\begin{align}
F_{2k}S_{2k}=F_2S_2+\sum_{n=2}^{n=k}\frac{1}{F_{2n}F_{2n-1}}=\sum_{n=1}^{n=k}\frac{1}{F_{2n}F_{2n-1}}
\end{align}
$$が成立し, 両辺を$F_{2k}$で割れば命題の式となる. $\quad\Box$
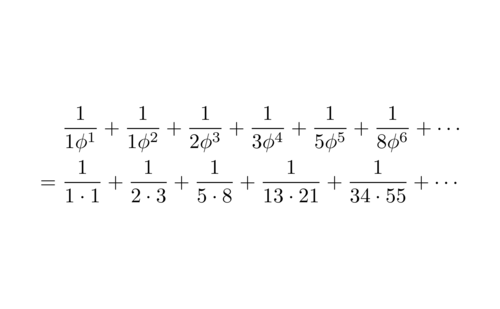
$\displaystyle\frac{1}{2}\sum_{n\geqslant1}^n\left|\frac{L_n}{F_n}-\sqrt{5}\right|=\sum_{n\geqslant1}^n\frac{1}{\phi^nF_n}=\sum_{n\geqslant1}^n\frac{1}{F_{2n}F_{2n-1}}$が成りたつ.
第一の等号は, 一般項および等式$-\bar{\phi}=1/\phi$を代入して
$$
\begin{align}
\sum_{n\geqslant1}^n\left|\frac{L_n}{F_n}-\sqrt{5}\right|&=\sum_{n\geqslant1}^n\left|\frac{L_n-\sqrt{5}F_n}{F_n}\right|\\
&=\sum_{n\geqslant1}^n\left|\frac{(\phi^n+\bar{\phi}^n)-(\phi^n-\bar{\phi}^n)}{F_n}\right|\\
&=\sum_{n\geqslant1}^n\left|\frac{2\bar{\phi}^n}{F_n}\right|=2\sum_{n\geqslant1}^n\frac{1}{\phi^nF_n}
\end{align}
$$
と計算することで証明される. また先の命題の極限の式
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{n+2k}F_n}=\frac{1}{F_{2k}}\sum_{n=1}^{n=k}\frac{1}{F_{2n}F_{2n-1}}
\end{align}
$$
において, 両辺に$F_{2k}$を掛けて$k\rightarrow\infty$なる極限を取り,
$$
\begin{align}
\lim_{k\to\infty}\frac{F_{n+2k}F_n}{F_{2k}}&=\lim_{k\to\infty}\frac{F_{n+2k}}{F_{n-1+2k}}\frac{F_{n-1+2k}}{F_{n-2+2k}}\cdots\frac{F_{2+2k}}{F_{1+2k}}\frac{F_{1+2k}}{F_{2k}}F_n\\
&=\phi^nF_n
\end{align}
$$を代入すれば第二の等号が得られる. $\quad\Box$
別の方向への一般化として, 次は
$$
\begin{align}
F_{n+2k}=a_kF_{n+k}+b_kF_n
\end{align}
$$の形の等式を構成して, それに基づいた計算結果を示す. 先ほどと同じく, 帰納的に$n\in\{0,1\}$の場合のみを考えて
$$
\begin{align}
\left(\begin{array}{l}F_{2k}=a_kF_{k}\\F_{1+2k}=a_kF_{1+k}+b_k\end{array}\right.
\end{align}
$$を解けば, その$a_k,b_k$はあらゆる$(k,n)$にも通用するはずである. Lucas 数および相互関係式$L_k=F_{k+1}+F_{k-1}$ (証明略), 二倍公式$F_{2k}=L_kF_k$ (加法定理から) を用いることで
$$
\begin{align}
a_k&=\frac{F_{2k}}{F_k}=L_k,\\
b_k&=F_{k+k+1}-L_kF_{k+1}\\
&=F_{k+1}F_{k+1}+F_kF_k-(F_{k+1}+F_{k-1})F_{k+1}\\
&=-(-1)^k
\end{align}
$$と解を表現できるため, 求めていた等式とは
$$
\begin{align}
F_{n+2k}=L_kF_k-(-1)^kF_n
\end{align}
$$
である.
任意の正整数$k,n$に対して, $F_{n+2k}=L_kF_{n+k}-(-1)^kF_n$が成りたつ.
$k$を固定して考える. $n\in\{0,1\}$のときに成立することは既知である. それぞれの等式について, ある$n+1,n$について等式が成りたつならば, それらを辺々足しあわせることで$n+2$の場合が得られ. また辺々を引けば$n-1$の場合が得られるので, 再帰的に命題は示された. $\quad\Box$
任意の正奇数$k$に対して, $S_{2k}=\displaystyle\frac{1}{L_k}\sum_{n=1}^{n=k}\frac{1}{F_{n+k}F_n}$が成りたつ.
$L_kF_{n+k}=F_{n+2k}-F_k$であることを用いれば
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{n+2k}F_n}&=\frac{1}{L_k}\sum_{n\geqslant1}^n\frac{F_{n+2k}-F_k}{F_{n+2k}F_{n+k}F_n}\\
&=\frac{1}{L_k}\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+k}F_n}-\frac{1}{F_{n+2k}F_{n+k}}\right)\\
&=\frac{1}{L_k}\sum_{n=1}^{n=k}\frac{1}{F_{n+k}F_n}
\end{align}
$$と計算できる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$1/F_{n+2k-1}F_n$の無限和
$S_3=\dfrac{1}{2}S_1-\dfrac{1}{4}$が成りたつ.
$S_1-2S_3$を考えると
$$
\begin{align}
S_1-2S_3&=\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+1}F_n}-\frac{2}{F_{n+3}F_n}\right)\\
&=\sum_{n\geqslant1}^n\frac{F_{n+3}-2F_{n+1}}{F_{n+3}F_{n+1}F_n}\\
&=\sum_{n\geqslant1}^n\frac{F_{n+2}-F_{n+1}}{F_{n+3}F_{n+1}F_n}\\
&=\sum_{n\geqslant1}^n\frac{1}{F_{n+3}F_{n+1}}\\
&=S_2-\frac{1}{F_3F_1}=1-\frac{1}{2}=\frac{1}{2}
\end{align}
$$のように計算することができ, これを$S_3$について観れば$S_3=\dfrac{1}{2}S_1-\dfrac{1}{4}$が得られる. $\quad\Box$
$S_5=\dfrac{2}{5}S_1-\dfrac{1}{75}$が成りたつ.
$2S_3-5S_5$を考えると
$$
\begin{align}
2S_3-5S_5&=\sum_{n\geqslant1}^n\left(\frac{2}{F_{n+3}F_n}-\frac{5}{F_{n+5}F_n}\right)\\
&=\sum_{n\geqslant1}^n\frac{2F_{n+5}-5F_{n+3}}{F_{n+5}F_{n+3}F_n}\\
&=\sum_{n\geqslant1}^n\frac{2F_{n+4}-3F_{n+3}}{F_{n+5}F_{n+3}F_n}\\
&=\sum_{n\geqslant1}^n\frac{2F_{n+2}-F_{n+3}}{F_{n+5}F_{n+3}F_n}\\
&=\sum_{n\geqslant1}^n\frac{F_{n+2}-F_{n+1}}{F_{n+5}F_{n+3}F_n}\\
&=\sum_{n\geqslant1}^n\frac{1}{F_{n+5}F_{n+3}}\\
&=S_2-\frac{1}{F_3F_1}-\frac{1}{F_4F_2}-\frac{1}{F_5F_3}\\
&=1-\frac{1}{2}-\frac{1}{3}-\frac{1}{10}=\frac{1}{15}
\end{align}
$$のように計算することができ, これを$S_5$について観れば$S_5=\dfrac{2}{5}S_1-\dfrac{1}{75}$が得られる. $\quad\Box$
より一般の$S_{2k-1}$も同様に計算することができる.
任意の正の整数$k$に対して, $F_{2k+1}S_{2k+1}-F_{2k-1}S_{2k-1}=1-\!\!\!\displaystyle\sum_{n=1}^{n+1=2k-1}\!\!\!\frac{1}{F_{n+2}F_n}$が成りたつ.
左辺を総和の中で通分すると
$$
\begin{align}
F_{2k-1}S_{2k-1}-F_{2k+1}S_{2k+1}&=\sum_{n\geqslant1}^n\left(\frac{F_{2k-1}}{F_{n+2k-1}F_n}-\frac{F_{2k+1}}{F_{n+2k+1}F_n}\right)\\
&=\sum_{n\geqslant1}^n\frac{F_{n+2k+1}F_{2k-1}-F_{n+2k-1}F_{2k+1}}{F_{n+2k+1}F_{n+2k-1}F_n}
\end{align}
$$
のようになるので, 加法定理を用いて分子を
$$
\begin{align}
&F_{n+2k+1}F_{2k-1}-F_{n+2k-1}F_{2k+1}\\
=\;&(F_{n+1}F_{2k+1}+F_nF_{2k})F_{2k-1}-(F_{n}F_{2k}+F_{n-1}F_{2k-1})F_{2k+1}\\
=\;&F_nF_{2k+1}F_{2k-1}-F_nF_{2k}^2=F_n\times(-1)^{2k}=F_n
\end{align}
$$を展開すれば, 元の式に代入して
$$
\begin{align}
F_{2k-1}S_{2k-1}-F_{2k+1}S_{2k+1}&=\sum_{n\geqslant1}^n\frac{1}{F_{n+2k+1}F_{n+2k-1}}\\
&=S_2-\!\!\!\displaystyle\sum_{n=1}^{n+1=2k-1}\!\!\!\frac{1}{F_{n+2}F_n}\\
&=1-\!\!\!\displaystyle\sum_{n=1}^{n+1=2k-1}\!\!\!\frac{1}{F_{n+2}F_n}
\end{align}
$$なる結果を得ることができる. $\quad\Box$
以上から, 再帰的に次の事実が判る.
任意の正の整数$k$に対して, $S_{2k}\in\mathbb{Q}$かつ$S_{2k-1}\in\{aS_1+b\mid a,b\in\mathbb{Q}\}$が成りたつ.
但し, $\mathbb{Q}$とは有理数の全体の集合であり, $\{aS_1+b\mid a,b\in\mathbb{Q}\}$は実数の全体の部分集合として扱っている.
($S_1$が無理数であるか否かは判りません... 何かご存じの方がいらっしゃればコメントなどでご教授いただけると嬉しいです. )
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
参考文献 (リンク付き)
1(
https://www.fq.math.ca/Scanned/7-2/brousseau1.pdf
) Brother Alfred Brousseau, "Summation of Infinite Fibonacci Series," The Fibonacci Quarterly, Vol.7 (1969), No.2; pp.143-168.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
