ゲージ対称性とは何か（３）: ネーターの定理まとめ＆コメント

前々回 ゲージ対称性とは何か（１）: ネーターの第１定理
前回 ゲージ対称性とは何か（２）: ネーターの第２定理
でネーターの定理を導きました。

ゲージ対称性には特にネーターの第２定理が重要でした。この定理から

ことが示せました。
これはE-L eqs.が独立ではないことを示します。
すなわち
ゲージ対称性が存在すると、運動が一意に定まらない
という事態が起きます。

ネーターの定理のまとめ

さて、前回までの記事、図もないし式も追いにくかったと思います。
本記事で、定理の証明の概要を簡単にまとめておきます。
比較として最初にオイラー・ラグランジュ方程式(E-L eqs.)の導出も記しておきます。

Notationに関しては以下です：

• 位置は$q^i$、速度は$\dot q^i$（ドットは時間微分）、運動量は$p_i$と表す。$i$は空間成分のindexであり、空間次元が$N$なら$i=1,\ldots,N$
• ある項に同じindexが2つ存在するとき（$q^ip_i$など）、そのindexに関して和をとっている
• 本来indexがついている変数に対しそれを省略したときは、その変数の集合を表す。例えば$q^i$に対し$q$と書いたら$\{q^i\}_{i=1,\ldots}$を表す

オイラー・ラグランジュ方程式とその証明

証明

• 変分空間

  • $\delta q$のみ考える
  • $\delta q(t_1)=\delta q(t_2)=0$
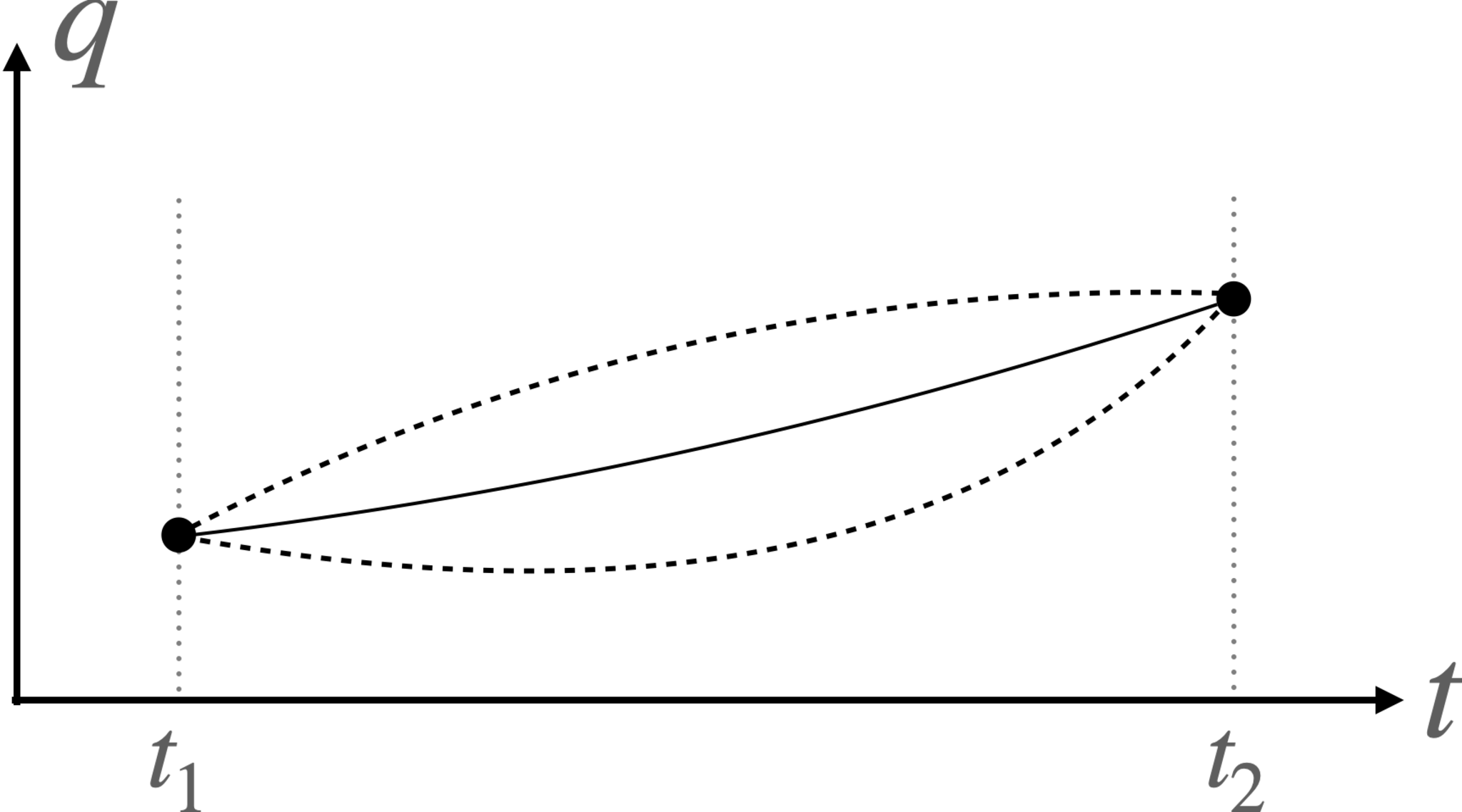    変分の概念図。実線が実際に実現する軌道。点線がそれに変分を加えた軌道。端は固定する。

• E-L eqsの導出の概要

  $S=\int^{t_2}_{t_1}L(q,\dot q, t)$に対して上記変分を行うと以下が導かれる：
  $$ \delta S=\int_{t_1}^{t_2} \left( \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q^i}\right)-\frac{\partial L}{\partial q^i} \right)\delta q(t)dt $$
  上式の導出では、$\delta q$が積分の端点でゼロなため表面項が消えることを使っている。これが任意の$\delta q$でゼロなので
  $$ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q^i}\right)-\frac{\partial L}{\partial q^i}=0 $$
  でなければならない。これがE-L eqs.

ネーターの第１定理とその証明

証明

• 変分空間：

  • $\delta q$および$\delta t$両方施す...積分の端点も変化
  • 端点における変分$\delta q(t_1), \delta q(t_2)$も任意

変分の概念図。線の意味は図1と同じ。変分により端も$q,t$方向に変化する。

• 変分に対する作用の変化：

  $$ \begin{align} \delta S[q,t]&=\int^{t_2}_{t_1}dt \left[ \left( \frac{\partial L}{\partial q^i}-\frac{d}{dt} \left(\frac{\partial L}{\partial \dot q^i} \right) \right) \bar \delta q^i +\frac{d}{dt} \left( \frac{\partial L}{\partial \dot q^i}\bar\delta q^i +L\delta t \right) \right]\\ &=\int^{t_2}_{t_1}dt \left[ \left( \frac{\partial L}{\partial q^i}-\frac{d}{dt} \left(\frac{\partial L}{\partial \dot q^i} \right) \right) (\delta q-\dot q \delta t) +\frac{d}{dt} \left( \frac{\partial L}{\partial \dot q^i}\delta q^i -\left( \frac{\partial L}{\partial \dot q^i}\dot q^i-L \right)\delta t \right) \right] \end{align} \tag{2} $$
  ここで$\bar \delta q$は、時間に関する変分を止めた、$q$の関数形の変化のみに関する変分。
  

• 定理の導出の概要：

  • Eq.(2)にE-L eqs.を課す→$\delta S[q,t]$の第１項消える
  • 変換により、任意の$t_1,t_2$で作用が不変だとすると
    $$ \Theta:= \frac{\partial L}{\partial \dot q^i}\delta q^i -\left( \frac{\partial L}{\partial \dot q^i}\dot q^i-L \right)\delta t $$
    として
    $$ \frac{d\Theta}{dt}=0 $$
    でなければならない。すなわち$\Theta$は保存。
    さらに$\delta q, \delta t$が
    $$ \begin{cases} \delta q =\epsilon^\alpha\phi_\alpha(q,\dot q,t)\\ \delta t =\epsilon^\alpha\tau_\alpha(q,\dot q,t) \end{cases} $$
    であるとする。ただし$\epsilon^\alpha$は定数、$\phi_\alpha,\tau_\alpha$はラグランジアンにより定まる関数。
    これを$\Theta$に代入すれば定理を得る。
  • 作用が準不変で
    $$ \delta S[q,t]=\int_{t_1}^{t_2}dt F(q,t) $$
    となるなら$\Theta-F$が保存。

ネーターの第２定理とその証明

証明

• 変分空間＆変分に対する作用の変化 : 第１定理と同じ

  • $\delta q$および$\delta t$両方施す...積分の端点も変化
  • 端点における変分$\delta q(t_1), \delta q(t_2)$も任意

変分の概念図。図2と同じ。変分により端も$q,t$方向に変化する。

• 定理の導出の概要：

  $\delta q, \delta t$が
  $$ \begin{cases} \delta q =\epsilon^\alpha(t)\phi_\alpha(q,\dot q)+\dot\epsilon^\alpha(t)\psi_\alpha(q,\dot q)\\ \delta t =\epsilon^\alpha(t)\tau_\alpha(q,\dot q) \end{cases} $$
  であるとし、これらに対して作用が準不変だとする：
  $$ \delta S=\int^{t_2}_{t_1}dt\left(\xi^\alpha(q,t)+\zeta^\alpha(q,t)\right) $$
  このときEq.(2)より
  $$ \begin{align} \int^{t_2}_{t_1}dt &\left[ \epsilon^\alpha \left\{ [L]_i(\phi^i_\alpha-\dot q^i\tau_\alpha) -\frac{d}{dt}(\psi^i_\alpha[L]_i) \right\} +\frac{d}{dt} \left\{ \epsilon^\alpha\psi^i_\alpha[L]_i +p_i\delta q^i -E\delta t -(\epsilon^\alpha\zeta_\alpha +\dot\epsilon^\alpha\eta_\alpha) \right\} \right] \equiv 0 \end{align} $$
  が成立。ある端点の組$t_1, t_2$に対し、$t_1< t< t_2$における$\epsilon^\alpha(t)$が任意であることから、第１項の$\epsilon^\alpha\{\ldots\}$の中括弧の中はゼロ。第２項は積分すると$t_1,t_2$に依存する表面項になる。$t_1, t_2$が任意であることから、第２項$\frac{d}{dt}\{\ldots\}$の中括弧の中はゼロ。さらに$\epsilon^\alpha(t),\dot \epsilon^\alpha(t)$が独立であることから
  $$ p_i\phi^i_\alpha-\tau_\alpha E-\zeta_\alpha+[L]_i\psi^i_\alpha\equiv 0,\tag{3}$$
  $$p_i\psi^i_\alpha-\eta_\alpha\equiv 0 $$
  が導かれる。

ゲージ対称性によりヘス行列の階数が下がることの証明

証明

第２定理における拘束条件Eq.(3)に含まれる$\ddot q^i$の項は、$[L]_i$のみに存在し、次の形をしている：
$$ A_{ij}\psi^i_\alpha\ddot q^j \ \ \ (\alpha=1,\ldots,R) , \ \ \ A_{ij}:=\frac{\partial^2 L}{\partial\dot q^i\partial \dot q^j} $$
Eq.(3)は恒等式だから、$\ddot q^j$の項の係数はゼロである:
$$ A_{ij}\psi^i_\alpha=0 $$
これは$A_{ij}$が$R$コのゼロ固有値を持つことを示している。

コメント

ネーターの第１定理に関して

第１定理に関し、上記のような変分を考えて導出するのは「やりすぎ」です。砂場のお山をショベルカーで作るような感じがします。
もっと単純に、ラグランジアンに$q\rightarrow q+\delta q$を施したときのラグランジアンの不変性から導くほうがわかりやすいです。この変換に対し
$$ \delta L(q,\dot q)=\frac{\partial L}{\partial q}\delta q + \frac{\partial L}{\partial \dot q}\delta \dot q $$
E-L eqs.$\frac{\partial L}{\partial q}=\frac{d}{dt}(\frac{\partial L}{\partial \dot q})$を用いれば
$$ =\frac{d}{dt}\left(\frac{\partial L}{\partial \dot q}\delta q\right) $$
となります。よって
$$ \Theta=\frac{\partial L}{\partial \dot q}\delta q $$
は保存します。

ゲージ理論における拘束条件に関して記載のある文献

私が眺めたことのある、ゲージ対称性と拘束条件に関する議論が載っている参考文献をRefs.[1-6]に挙げました。

• Ref.[1]: これまでの記事はこの文献を元にしています。
• Ref.[2]: 場の理論におけるネーターの第２定理について書いてあります。
• Ref.[3]: これはRef.[1]を微分形式を用いて書いたもの。
• Ref.[4]: 多様体論・微分形式を用いて古典力学（一部量子論）の様々な分野を網羅的に取り扱っています。
• Ref.[5]: ゲージ場の量子論に関する本なので、拘束系の取り扱いについてはそれほど多く書いてあるわけではありません。しかしだからこそ非常にコンパクトに、わかりやすくそれに関して書かれています。読みやすいのではないかと思います。
• Ref.[6]: ゲージ理論における拘束系の話題について様々なトピックを扱っています。この分野の教科書としては今や定番なのではないでしょうか。

Ref.[1]のDiracの予想に対する記述に関して

以下未説明の概念がいくつかありますがご容赦ください。

Diracの予想とは「ゲージ対称性の生成関数は第１類拘束条件全てである」というものです。Diracは1次拘束条件, 2次拘束条件の区別なく、第１類の拘束条件を同等に扱って良いと主張しました。
その後この予想の反例がいくつか見つかりました。よって、一般にはこの予想は正しくないのだと思います。ただしこれらの反例は大変特殊な系であり、力学的にまともな系ではDiracの予想は成立していると言って良いようです。

ところでRef.[1]において筆者の方は「ゲージ対称性の生成関数は第１類第１次拘束条件である」と主張しています。第１次・２次拘束の違いを重要視しています。
Diracの予想は一般には正しくないですが、このような主張は他の教科書には見られないようです。これに関し、私にはRef.[1]が正しいか判断できません。

決してこの本を貶めたいわけではないし、間違っていると言いたいのでもありません。
筆者の方およびその共同研究者の方は、その分野で著名な方々です。
この主張に関し長年研究され、様々な研究者との議論を積み重ねていらっしゃいます。
もちろん一連の研究論文は学術雑誌に掲載されています。

また、ゲージ理論における拘束条件を専門に扱う日本語の教科書は少なく（私はこの本以外知りません）、これを学ぶのにRef.[1][3]が大変有用であることは間違いないです。

参考文献として挙げたので、一言言及しておくべきかと思い記しました。

次回予告

次はDiracの方法、またはU(1)ゲージ理論（Maxwell方程式）に関してお話しようかと思います。

☆次の記事: ゲージ対称性とは何か（４）: ゲージ理論の解法の概観