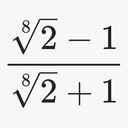ζ’(1/2)/ζ(1/2)
定義
| 記号 | 名称、Wikipedia |
|---|---|
| $\delta_{a,b}$ | クロネッカーのデルタ |
| $L(s,f)$ | L関数 |
| $\chi(n)$ | ディリクレ指標 |
| $G(\chi)$ | ガウス和 |
| $\tau(n)$ | ラマヌジャンのタウ関数 |
ディリクレのL関数
$\chi$を法$N$の原始ディリクレ指標とする。
$\chi(-1)\in\{1,-1\}$
$a\coloneqq\frac{1-\chi(-1)}2$
$\lr({\dfrac\pi N})^{-\frac s2} \Gamma\lr({\dfrac{s+a}2})L(s,\chi) =
\dfrac{G(\chi)}{i^a\sqrt N}\lr({\dfrac\pi N})^{-\frac{1-s}2} \Gamma\lr({\dfrac{1-s+a}2})L(1-s,\overline\chi)$
$\chi$が法$1$の自明な指標である時、リーマンゼータ関数の関数等式そのものになります。
ディリクレのL関数(英語版Wikipedia)
、
特殊関数 グラフィックスライブラリー
、『
ディリクレのL関数の特殊値と関数等式
』より。
$n\in\N_0$
$\beginend{alignat}{2
&{\rm Re}\lr[{\lr.{\lr({\frac{L'(s,\chi)}{L(s,\chi)}})^{(2n)}}|_{s=\frac12}}] &&=
\frac{\delta_{n,0}}2\ln\frac\pi N -
2^{-2n-1}\psi^{(2n)}\lr({\frac{2-\chi(-1)}4}) \\
&{\rm Im}\lr[{\lr.{\lr({\frac{L'(s,\chi)}{L(s,\chi)}})^{(2n+1)}}|_{s=\frac12}}] &&= 0
}$
関数等式を対数微分し移項すれば、
$\dfrac{L'(s,\chi)}{L(s,\chi)} + \dfrac{L'(1-s,\overline\chi)}{L(1-s,\overline\chi)} =
\ln\dfrac\pi N - \dfrac12\lr({\psi\lr({\dfrac{s+a}2}) + \psi\lr({\dfrac{1-s+a}2})})$
$k$階微分して$s=\frac12$を代入すれば、
$\lr.{\lr({\dfrac{L'(s,\chi)}{L(s,\chi)}})^{(k)}}|_{s=\frac12} +
(-1)^k\lr.{\lr({\dfrac{L'(s,\overline\chi)}{L(s,\overline\chi)}})^{(k)}}|_{s=\frac12} =
\delta_{k,0}\ln\dfrac\pi N -
\lr[{1+(-1)^k}]2^{-k-1}\psi^{(k)}\lr({\dfrac{2-\chi(-1)}4})$
$\lr.{\lr({\dfrac{L'(s,\overline\chi)}{L(s,\overline\chi)}})^{(k)}}|_{s=\frac12} =
\overline{\lr.{\lr({\dfrac{L'(s,\chi)}{L(s,\chi)}})^{(k)}}|_{s=\frac12}}$であるため、
$\lr.{\lr({\dfrac{L'(s,\chi)}{L(s,\chi)}})^{(k)}}|_{s=\frac12} +
(-1)^k\overline{\lr.{\lr({\dfrac{L'(s,\chi)}{L(s,\chi)}})^{(k)}}|_{s=\frac12}} =
\delta_{k,0}\ln\dfrac\pi N -
\lr[{1+(-1)^k}]2^{-k-1}\psi^{(k)}\lr({\dfrac{2-\chi(-1)}4})$
${\rm Re}\ z = \dfrac{z+\overline z}2,{\rm Im}\ z = \dfrac{z-\overline z}2$を適用する。
$n=0$の時は、
$\psi\lr({\dfrac{2\pm1}4}) = -\gamma-3\ln2\pm\dfrac\pi2$であるため、
$\beginend{align}{
{\rm Re}\frac{L'(\frac12,\chi)}{L(\frac12,\chi)} &=
\frac12\lr({\ln\frac\pi N-\psi\lr({\frac{2-\chi(-1)}4})}) \\&=
\frac12\lr({\gamma+\ln\frac{8\pi}N})+\chi(-1)\frac\pi4}$
$n\ge1$の時は、
$\psi^{(2n)}\lr({\dfrac{2\pm1}4}) = 2^{2n-1}\lr[{-2\lr({2^{2n+1}-1})(2n)!\zeta(2n+1)\pm|E_{2n}|\pi^{2n+1}}]$であるため、
$\beginend{align}{
{\rm Re}\lr[{\lr.{\lr({\frac{L'(s,\chi)}{L(s,\chi)}})^{(2n)}}|_{s=\frac12}}] &=
-2^{-2n-1}\psi^{(2n)}\lr({\frac{2-\chi(-1)}4}) \\&=
\frac{\lr({2^{2n+1}-1})(2n)!\zeta(2n+1)}2 +
\chi(-1)\frac{|E_{2n}|\pi^{2n+1}}4
}$
$\chi$が法$1$の自明な指標の場合は$L(s,\chi)=\zeta(s)$なので、
$\beginend{align}{
\frac{\zeta'\lr({\frac12})}{\zeta\lr({\frac12})} &=
\frac{\gamma+\ln(8\pi)}2+\frac\pi4 \\
\lr.{\lr({\frac{\zeta'(s)}{\zeta(s)}})''}|_{s=\frac12} &=
7\zeta(3)+\frac{\pi^3}4 \\
\lr.{\lr({\frac{\zeta'(s)}{\zeta(s)}})''''}|_{s=\frac12} &=
372\zeta(5)+\frac{5\pi^5}4
}$
となります。$0$階微分の値は英語版Wikipediaの
『
Particular values of the Riemann zeta function
』にも載っています。
ポリガンマ関数の特殊値:
英語版Wikipedia
、『
ポリガンマ関数の特殊値(1/2,1/4,3/4,1/3,2/3)
』
ラマヌジャンのL関数
$(2\pi)^{-s} \Gamma(s)L(s,\tau) = (2\pi)^{-12+s} \Gamma(12-s)L(12-s,\tau)$
ラマヌジャンのL関数(英語版Wikipedia) 、 特殊関数 グラフィックスライブラリー より。
$\lr.{\lr({\dfrac{L'(s,\tau)}{L(s,\tau)}})^{(2n)}}|_{s=6} = \delta_{n,0}\ln(2\pi)-\psi^{(2n)}(6)$
関数等式を対数微分し移項すれば、
$\dfrac{L'(s,\tau)}{L(s,\tau)} + \dfrac{L'(12-s,\tau)}{L(12-s,\tau)} =
2\ln(2\pi) - \psi(s) - \psi(12-s)$
これを$2n$階微分して$s=6$を代入する。
$\displaystyle \psi^{(2n)}(6) = \psi^{(2n)}(1) + (2n)!\sum_{k=1}^5 k^{-2n-1}$であるため、
$\beginend{align}{
\lr.{\lr({\frac{L'(s,\tau)}{L(s,\tau)}})^{(2n)}}|_{s=6} &=
\delta_{n,0}\ln(2\pi) - \psi^{(2n)}(1) - (2n)!\sum_{k=1}^5 k^{-2n-1} \\&=
(2n)!\lr({\zeta(2n+1) - \sum_{k=1}^5 k^{-2n-1}})
\quad(n\ge1)
}$
$\beginend{align}{ \frac{L'(6,\tau)}{L(6,\tau)} &= \gamma+\ln(2\pi)-\frac{137}{60} \\ \lr.{\lr({\frac{L'(s,\tau)}{L(s,\tau)}})''}|_{s=6} &= 2\zeta(3)-\frac{256103}{108000} \\ \lr.{\lr({\frac{L'(s,\tau)}{L(s,\tau)}})''''}|_{s=6} &= 24\zeta(5)-\frac{806108207}{32400000} }$