OMCG002(L)に関する構図とその拡張について
みなさんこんばんはかえでです.
今回は,
OMCG002(L)
について話していこうと思います.この問題はOMCG002のボス問題で,点数もOMC最高の1000点.Writer陣もこの問題の解決には4ヶ月の期間を要したとのことで間違いなくOMC最難問のひとつなのですが,実は構図の知識があれば比較的容易にこの問題を解くことが出来ます.ただしこの記事ではsolvingもそうですが,特に関連構図の方について話していきます.
本題
まず,問題を見ていきましょう.(見た目の観点から点の名前をほんの少し変えています)
$AB \lt AC$なる鋭角三角形$ABC$の外接円を$\Gamma$,外心を$O$,$\angle A$内の傍心を$I_A$,傍接円を$\omega_A$とします.$\omega_A$と直線$CA,AB$の接点をそれぞれ$E,F$とすると,直線$BE,CF$は$\Gamma$上の点$X$で交わりました.直線$I_AX$と$\Gamma$が再び交わる点を$Y$とし,線分$YI_A$の垂直二等分線と直線$YO$の交点を$Z$とします.
$(1)$ 三角形$ABC$の垂心を$H$とします.以下が成り立つとき,線分$HZ$の長さの二乗は互いに素な正の整数$a,b$を用いて$\dfrac{a}{b}$と表せます.
・$OZ=4$
・$\omega_A$の半径は$9$
$(2)$ $A$から直線$BC$に下ろした垂線の足を$T$とし,直線$AZ$と$\Gamma$が再び交わる点を$P$とします.以下が成り立つとき,$\dfrac{AZ}{ZP}$の値は互いに素な正の整数$c,d$を用いて$\dfrac{c}{d}$と表せます.
・$|\triangle ACZ|-|\triangle ABZ|=3$
・$|\triangle ACT|-|\triangle ABT|=13$
$ab+cd$の値を解答してください.ただし,$|\triangle LMN |$で三角形$LMN$の面積を表します.
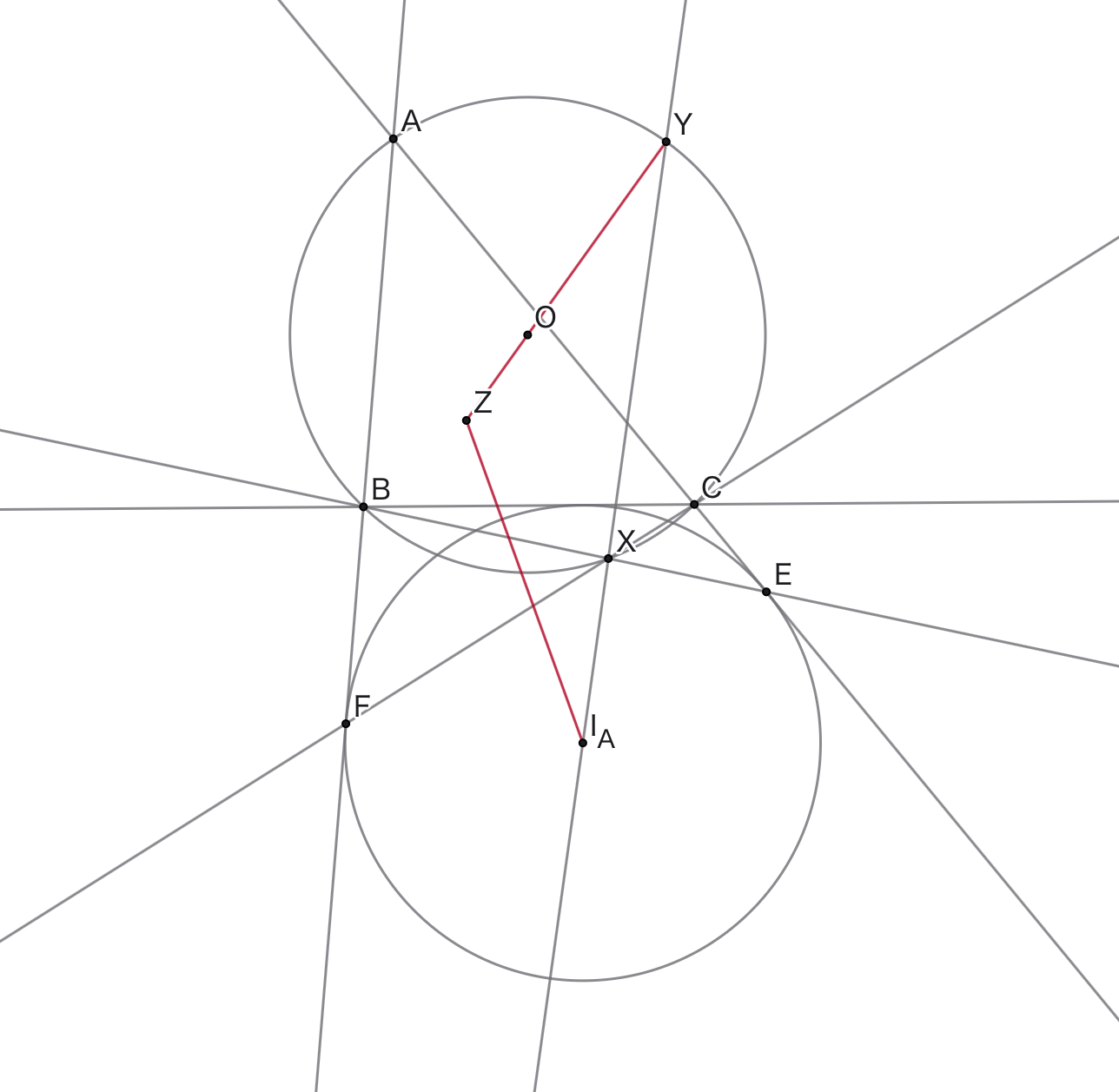 見やすい図
見やすい図
長すぎです.一つの問題の中で問題が二部作になってるのはさすがにヤバすぎですが,実はこの問題は構図さえ理解できれば,さらに言えば$Z$について理解できれば,求値パートは殆どやるだけです.なので求値パートは無視して問題で与えられた条件下での構図について考えていきましょう.
構図を考える
以下,構図の話をしていきますが,円錐曲線などの難しい話がたくさん登場します.出来るだけ説明しながら話していきますが,もしそれでも理解が大変であれば,先に弊記事 Feuerbach点について をご覧いただければ理解が容易くなると思います.
さて,考察対象は直線$BE$と直線$CF$の交点($A$-外Gergonne点)が円$ABC$上にある場合ですね.
ここで,三角形$ABC$の$A$-外Feuerbach双曲線を$\mathcal{H}_A$,$A$-外Feuerbach点を$Fe_A$とでもしましょう.つまり,$A,B,C,H,I_A$を通る直角双曲線を$\mathcal{H}_A$とし,その中心を$Fe_A$とします.
このとき,有名事実として一般に以下が成り立ちます.
直線$BE$と直線$CF$の交点$X$は$\mathcal{H}_A$上にある.
定理1が成り立つことから,これは$X$が円$ABC$と$\mathcal{H}_A$の第四交点と一致するときを考える問題であると分かります.点が一致するような束縛条件を考える問題は,一致する二点それぞれの一般に成り立つ性質を考え,後からどう振る舞うのかを見るのが鉄則です.なので,円$ABC$と$\mathcal{H}_A$の第四交点を$S$として,$X$と$S$の性質をそれぞれ調べていきましょう.
第四交点$S$について
まず,第四交点$S$について考えましょう.
簡単のため,以下で扱う定理2においては傍心$I_A$を内心$I$に,外Feuerbach双曲線$\mathcal{H}_A$をFeuerbach双曲線$\mathcal{H}$に置き換えて考えようと思います.内心と傍心は三角形幾何的には実質等しい概念で,全く同様の主張がそれぞれで成り立つからですね.
突然ですが,次の定理が成り立ちます.
三角形$ABC$の内心を$I$,外心を$O$とする.三角形$ABC$におけるEuler線の反Steiner点を$Eu$とするとき,直線$SEu$は線分$OI$の中点を通る.
何に使うのかはまだ分からなくて大丈夫です.とりあえずこれを証明していきましょう.
垂心を$H$とする三角形$ABC$と点$P$について,直線$PH$の反Steiner点$X$と点$P$を結ぶ直線は直角双曲線$ABCPH$と円$ABC$の第四交点$S$を通る.
$S(A,B;C,P) =$$ H(A,B;C,P) \overset{Steiner}{=} $$(A,B;C,X) \overset{\odot(ABC)}{=} $$S(A,B;C,X)$となるのでよい.$\blacksquare$
三角形$ABC$の九点円心を$N$,Kosnita点を$Ko$,Euler線の反Steiner点を$Eu$とする.このとき,三点$N,Ko,Eu$は共線である.
Sublemma : 三角形$ABC$およびそのEuler線上の点$P$について,$P$- Hagge円 の中心を$O_P$とし,Euler線の反Steiner点を$Eu$とする.このとき,三点$P,O_P,Eu$は共線である.
Proof : 三角形$ABC$における$P$の circumcevian triangle を$DEF$とし,$P$-Hagge円を$D'E'F'$とする.このとき,有名事実として$\triangle DEF \cup P \overset{-}{\sim} \triangle D'E'F' \cup P$が成り立つから,三角形$ABC$の外心を$O$とすれば$\measuredangle D'PO_P = \measuredangle OPD$が従う.一方直線$BC$について$Eu$と対称な点を$Eu'$とすれば,反Steiner点に関する有名事実から五点$P,D,D',Eu,Eu'$の共円が成り立つから,$\measuredangle OPD = \measuredangle D'PEu$となって示される.$\blacksquare$
主題の証明 : Properties of Hagge circle (Corollary 1.1)より,$N$-Hagge円の中心$O_N$は$N$について$Ko$と対称な点である.一方Sublemmaにおいて $P=N$とすれば三点$N,O_N,Eu$の共線が従う.よって特に三点$N,Ko,Eu$は共線である.$\blacksquare$
三角形$ABC$について,そのSchiffler点を$Sc$とし,円$ABC$における弧$BC,CA,AB$の南極点をそれぞれ$V_A,V_B,V_C$とする.このとき,$Sc$は三角形$V_AV_BV_C$のKosnita点である.
三角形$ABC$の内心を$I$,$\angle A$内の傍心を$I_A$,外心を$O$,三角形$BIC$の垂心を$H$,円$V_BOV_C$の中心を$O'$,円$V_BOV_C$における$O$の対蹠点を$W$とし,線分$BC,IH$の中点をそれぞれ$M,N$とする.今,四角形$HNV_AM$は平行四辺形であるから$V_AN \parallel MH$である.よって,明らかに三点$H,M,I_A$は共線であるから直線$V_AN$は三角形$V_AV_BV_C$の$V_A$-Symmedianであり,三点$V_A,N,W$の共線が従う.したがって
$V_A(O,W;O',\infty_{\perp V_BV_C}) = -1 = V_A(\infty_{\perp BC},N;H,I) = V_A(O,W;H,\infty_{\perp V_BV_C})$
となり,三点$V_A,H,O'$の共線が従う.これは三角形$BIC$のEuler線が三角形$V_AV_BV_C$のKosnita点を通ることを表しているので,特に$Sc$が三角形$V_AV_BV_C$のKosnita点であることが示される.$\blacksquare$
さて,これらを用いて"三角形$ABC$におけるEuler線の反Steiner点を$Eu$とするとき,直線$SEu$は線分$OI$の中点を通る."ことを示していきましょう.
三角形$ABC$のSchiffler点を$Sc$とします.このとき,$Sc$は三角形$ABC$のEuler線と$\mathcal{H}$の交点です.よって補題3より三点$S,Sc,Eu$は共線であると分かるので,直線$SSc$が線分$OI$の中点を通ることを示せば十分です.ここで,直線$AI,BI,CI$と円$ABC$が再び交わる点をそれぞれ$V_A,V_B,V_C$とすれば,$S$は三角形$V_AV_BV_C$におけるそのEuler線の反Steiner点であることが容易に確認でき,さらに線分$OI$の中点は三角形$V_AV_BV_C$の九点円心であると分かります.よって補題5より$Sc$が三角形$V_AV_BV_C$のKosnita点であることに留意すれば,補題4より直線$SSc$が線分$OI$の中点を通ることが示されます.$\blacksquare$
面白い構図ですね.また,図の簡単のために再び$I_A$と$\mathcal{H}_A$に対象を戻して考えると,次のような構図が成り立ちます.(内心側でも当然成り立ちますが,こればかりは外側で考えた方が後々の見通しがよいです.)
直線$I_AS$と円$ABC$が再び交わる点を$Y$とし,直線$YO$と直線$I_AFe_A$の交点を$Z$としたとき,$ZY=ZI_A$が成り立つ.
直線$SO$と直線$I_AFe_A$が平行であることを示せばよいが,これは三角形$ABC$の九点円心を$N$としたときに,直線$Fe_AN$を垂心$H$を中心に$2$倍に拡大した像が直線$SO$に等しいことと,三点$I_A,Fe_A,N$が共線であることから明らかである.$\blacksquare$
直線$BC$上の点$L$を$LI_A=LY$となるように取ったとき,$\triangle YAZ \overset{+}{\sim} \triangle YZL$が成り立つ.
直線$AI_A$と円$ABC$が再び交わる点を$V$とするとき,三角形$YVI_A$の外心が$L$であることを示せばよい.さらに,Typicalな議論を考えれば直線$BC$について$V$と対称な点を$V'$としたときに,四点$I_A,V,V',Y$が共円であることを示せばよいが,これは Feuerbach点について の定理40から明らかである.$\blacksquare$
また,定理7から以下が従います.
直線$AZ$と直線$LS$は円$ABC$上で交わる.
もう少し色んな構図が導けそうですが,OMCG002に直接関係してくるものとしてはこのくらいで十分でしょう
.
では,次にGergonne点$X$について考えていきます.
Gergonne点$X$について
まず,明らかなこととして,$A$-傍接円$\omega_A$と直線$BC$の接点を$D$としたとき,三点$A,D,X$は共線です.なのでこの直線と円$ABC$が再び交わる点を$P$とし,さらに直線$EF$と直線$BC$の交点を$J$,直線$JP$と円$ABC$が再び交わる点を$Q$とします.
このとき,以下が自明に成り立ちます.
直線$AQ$は$A$-Symmedianである.
四角形$ABQC$が調和四角形であることを示せばよく,これは$P$を中心とする円$ABC$から直線$BC$への射影を考えればcevianに関する調和点列から明らかである.$\blacksquare$
はい,Gergonne点に関する構図は以上です.
$Z$について
では,問題で与えられた条件$S=X$を適用し,このときの$Z$について考えましょう.まず,以下の二つが成り立つことが分かります.(これらは公式解説でも簡単に証明されているので,証明はそちらを参考にしてください)
$A$-傍接円と円$ABC$の半径は等しい
$L=J$である.
これらを認めた上で,次の主張を証明します.
$Z$は三角形$ABC$の類似重心である.
命題10より四角形$I_AXOFe_A$は平行四辺形であるから直線$XFe$は線分$OI_A$の中点を通る.よってこの直線と円$ABC$が再び交わる点を$W$とすれば定理2より$W$における三角形$ABC$のSteiner線はEuler線に等しく,さらに補題3よりこのSteiner線は$\mathcal{H}_A$の$H$における接線である.ところで直線$OI_A$も$\mathcal{H}_A$に接しているから,$O$は三角形$ABC$における$I_A,H$の
crosspoint
であると分かる.(なお,このcrosspointは三角形$DEF$の垂心であるので実はここまでの議論は問題を解くだけなら不必要である.これが構図の知識があればこの問題を容易に解けると言った所以である.)
また,有名事実としてこのcrosspointの
complement
は$I_A$と三角形$ABC$の類似重心$K$を結ぶ直線上にあるので,結局$N,K,I_A$の共線が従う.特に,定理6より$I_A,Fe,Z,K$を通る直線が存在する.
ところで,命題11と定理8より直線$AZ$は$Q$を通るから,定理9より直線$AZ$は$A$-Symmedianである.以上より,$Z=K$であり,$Z$が三角形$ABC$の類似重心であることが示される.$\blacksquare$
はい,このような感じで$Z$の正体が類似重心であることが分かり,1000点問題が解決されました.証明中にも述べましたが,問題を解くだけなら$X(64)$がcrosspointなので〜とやれば一瞬で終わるんですね.なので証明に4ヶ月がかかったという公式解説の証明方法よりはこれの方がずっと容易だと思います.
では,次にこの問題の構図をまた別の視点から一般化していきましょう.
問題の自然な拡張
この問題は,$I_A$の垂足三角形と三角形$ABC$のperspectorが円$ABC$上にあるときに,どういう構図が成り立つか?というものでした.なので,拡張として一般の三角形$ABC$におけるLucas三次曲線と劣弧$BC$の交点を考えたくなります.Lucas三次曲線というのは,三角形$ABC$における
チェバ三角形
がある点の垂足三角形になるような点の集合です.(Lucas三次曲線はCatalogue of Triangle CubicsではK007に分類されていて,GeogebraではCubic(A,B,C,7)で描くことが出来ます(ただし,円との交点を取れない,それ上の点が勝手に動くなど,まともな挙動をしてくれません)).
OMCG002(L)ではこの交点が外Gergonne点であったということです.実際に図を描いてみると色々なことが成り立っていそうであることが分かったので,Lucas三次曲線とDarboux三次曲線(垂足三角形が基準三角形とperspectiveになるような点の軌跡)の対応に留意しながら見ていきましょう.
構図たち
不等辺鋭角三角形$ABC$について,そのLucas三次曲線と劣弧$BC$の交点を$R$,$R$の
cevian triangle
を$DEF$,三角形$ABC$と三角形$DEF$の三角形$DEF$側の
orthology center
を$P$,三角形$ABC$における$P$の等角共役点を$Q$とする.また,三角形$ABC$の重心を$G$,外心を$O$,垂心を$H$,九点円心を$N$,類似重心を$K$,de Lonchamps点を$L$とし,四点形$ABCR$の
Poncelet点
を$X$,$Q$の垂足三角形を$Q_AQ_BQ_C$とする.$\cdots (\bigstar)$
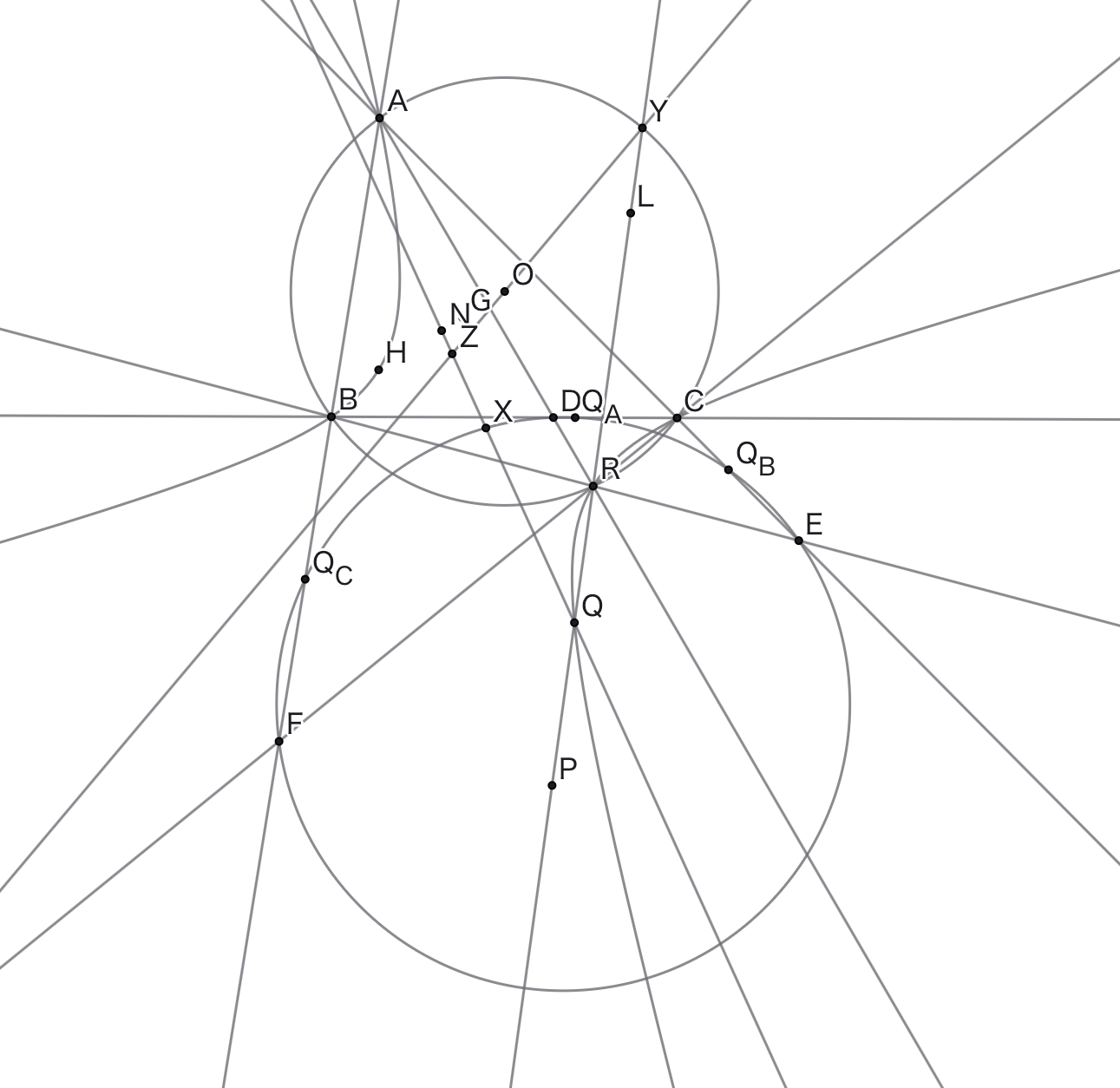 何が成り立っているでしょうかクイズ
何が成り立っているでしょうかクイズ
四点の組$(A,O,D,P), (B,O,E,P), (C,O,F,P)$はそれぞれ共円である.
これはかなり面白い構図なので,先ほどと同じく遠回りしながら示していこうと思います.
三角形$ABC$とその Antigonal conjugate の組$(P,Q)$について,$P,Q$の三角形$ABC$における等角共役点をそれぞれ$P',Q'$とするとき,これら二点は円$ABC$における反転で移り合う.
これをAntigonal conjugateの定義にすることもありますが,僕は点$P$のAntigonal conjugateを直角双曲線$ABCP$における$P$の対蹠点と定義しているので,今回は補題とします.この補題はかなり便利なので覚えておきましょう.
三角形$ABC$と点$P$について,$P$の三角形$ABC$におけるcevian triangleを$DEF$とし,$P$の三角形$ABC$における Miquel associate を$R$とする.このとき,三円$ADR,BER,CER$は$P$の三角形$ABC$におけるantigonal conjugateの等角共役点で交わる.
補題14および Miquel triangle and Isogonal center のProperty 10より円$ADR$が四点形$ABCP$のIsogonal centerを通ることを示せばよく,これは同リンク先のProperty 4にて証明されている.$\blacksquare$
三角形$ABC$とそのDarboux三次曲線上の等角共役点の組$(P,Q)$について,$P$の垂足三角形と三角形$ABC$のperspectorを$R$とする.このとき,$Q,R$は三角形$ABC$の同一外接直角双曲線上に乗る
Remark: Darboux三次曲線はde Longchamps点をpivotとする pivotal isogonal cubic であること,つまり,$(\bigstar)$の定義において$P,Q,R,L$は共線であることが知られています.以降これが前提知識となってくるので抑えておきましょう.
さて,これらを用いれば,とある有名構図の一般化である以下の定理が証明出来ます.(調べてもあまり出てこなかったのでもしかしたら自分が世界で初めて証明した人間かもしれません)
外心を$O$とする三角形$ABC$とそのDarboux三次曲線上の点$P$について,円$BPC$における$P$の対蹠点を$P'$とし,直線$BP',CP'$が対辺と交わる点をそれぞれ$U,V$とする.このとき,直線$PO$と直線$UV$は直交する.
$P$を内心や傍心とすれば,超有名なあの構図になります.
参考 :
外心と傍心を結ぶ直線に垂直な直線
,
自己紹介&とある有名問題の証明
$P$の等角共役点を$Q$,垂足三角形を$DEF$とし,$R=AD \cap BE \cap CF$とする.このとき四点の組$(B,P,E,U),(C,P,F,V)$はそれぞれ共円であるので,$P$から直線$UV$に下ろした垂線の足$I$は四点形$ABCR$のIsogonal centerであると分かる.よって補題15から$I$の等角共役点が直角双曲線$ABCR$上に乗るが,ところで補題16よりこの直角双曲線は$Q$を通るので,この直角双曲線の等角共役を考えれば三点$P,O,I$は共線であり,特に$PO \perp UV$が示される.$\blacksquare$
これ,めちゃくちゃ面白いですよね.ちなみに直線$UV$の円$ABC$における極の等角共役点が$R$であることも補題14により従います.
では命題13の証明をしていきますが,実はこれはここまでの補題から自明で,今$R$が円$ABC$上にあることから$R$のAntigonal conjugateは$H$であり,その等角共役点は$O$なので補題15により証明完了です.$\blacksquare$
OMCG002(L)の公式解説にこれと対応する主張があることには留意すべきでしょう.
また,$O$は四角形$ABRC$のIsogonal centerであると同時に,同四角形のGergonne-Steiner pointおよびPseudocircumcenterでもあるという事実(共円なので自明だが,一般的な構図を考える上では)重要かと思います.
では次に,以下の自明に等価な命題族を示していきます.なんと,これらはOMCG002(L)公式解説で扱っている主張族と完璧に対応しています.
$QX:XN=2:1$である.
$QR:RL = 1:2$である.
四角形$QXOR$は平行四辺形である.
直線$QX$は$N$を通る.
直線$QR$と円$ABC$が再び交わる点を$Y$とし,直線$YO$と直線$QX$の交点を$Z$とするとき,$ZY=ZQ$である.
これらのうちひとつでも従えばその他も即座に従うというのは比を追えば容易に分かります.
どれも証明は非常に難しいのですが,$QX:XN=2:1$を示す方針がおそらく一番出来る可能性が高いのでこの方針で議論をしていきたいと思います.というのも,より一般に以下の構図が成り立つためです.
三角形$ABC$とその外接円上の点$P$について,$P$のcevian triangleを$DEF$とし, cyclocevian conjugate を$Q$とする.また,線分$PH$の中点を$T$とし,$Q$のMiquel associateを$K$とする.このとき,線分$TK$の長さは円$ABC$の外接円の半径に等しい.
これを証明することを目標に,色々な補題を見ていきましょう.
まず,前提知識として以下の有名事実を載せておきます.
三角形$ABC$と点$P$について,$P$のcevian triangleの外接円は四点形$ABCP$とPoncelet点を通る.
以下ではこれを認めて議論をしていきます.Feuerbach点の記事にも載ってたやつですね(多分).では次へ.
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P$のcevian triangleを$DEF$とし,三角形$ABC$と三角形$DEF$の perspectrix を$\overline{XYZ}$とする.このとき,完全四辺形$\{ EF,FD,DE,\overline{XYZ} \}$のMiquel点$T$は四点形$ABCQ$のPoncelet点である.
Sublemma : 三角形$ABC$と点$P$について,$P$のcevian triangleを$DEF$とし,三角形$ABC$と三角形$DEF$のperspectrixを$\overline{XYZ}$とする.このとき,完全四辺形$\{ EF,FD,DE,\overline{XYZ} \}$のMiquel点は三角形$ABC$の九点円上にある.
proof :
Nine-point circle, pedal circle and cevian circle
(Proposition 10)にて証明されている.$\blacksquare$
主題の証明 : 三角形$ABC$の外心を$O$,三角形$DEF$の垂心を$H_P$とすれば,Sublemmaより$T$は三角形$DEF$および三角形$ABC$の中点三角形における直線$OH_P$の反Steiner点であると分かる.一方三角形$ABC$における$Q$の等角共役点を$Q'$とすれば,Tran Quang Hungの結果から三点$O,Q',H_P$は共線であるので,$T$は三角形$ABC$における直線$OQ'$の反Steiner点であると分かり,特にPoncelet点に関する有名事実からこれは四点形$ABCQ$のPoncelet点である.$\blacksquare$
外心を$O$とする三角形$ABC$と等角共役点の組$(P,Q)$について,四点形$ABCP$のPoncelet点を$T$とし, cyclocevian triangle を$XYZ$とする.このとき,三角形$XYZ$における$T$のSteiner線は直線$OQ$に等しい.
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,直線$P_AP,P_BP,P_CP$が円$P_AP_BP_C$と再び交わる点をそれぞれ$N_A,N_B,N_C$とする.このとき,内接四角形$Q_AP_BN_AP_C, Q_BP_CN_BP_A, Q_CP_AN_CP_B$は調和四角形である.
$L=AP \cap P_BP_C, $$ S= BC \cap P_BP_C$とし,線分$P_BP_C$の中点を$M$とする.このとき,$(P_B,P_C;S,L) \overset{A}{=} (B,C;S,P_A) \overset{cevian}{=} -1$なので$SL \times SM = SP_B \times SP_C = SQ_A \times SP_A$となって,四点$P_A,Q_A,L,M$の共円が従う.よって
$\measuredangle Q_AMP_B =$$ \measuredangle Q_AML =$$ \measuredangle Q_AP_AL =$$ \measuredangle Q_AP_AN_A =$$ \measuredangle Q_AP_CN_A$
となって示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$Q$のcevian triangleを$Q_AQ_BQ_C$とし,四点形$ABCP$のPoncelet点を$T$,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$とする.また,$A$から直線$BC$に下ろした垂線の足を$A'$とし,$A$-midlineと直線$\overline{XYZ}$の交点を$X'$とする.このとき,四点$T,X',X,A'$は共円である.
Nine-point circle, pedal circle and cevian circle (Proposition 12)にて証明されている.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P$のcevian triangleを$P_AP_BP_C$,四点形$ABCQ$のPoncelet点を$T$とし,$A$-midlineを$m_a$とする.このとき,$T$は完全四辺形$\{ P_BP_C,P_CP_A,P_AP_B,m_a \}$のMiquel点である.
補題25よりSteiner線の存在性から明らかである.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,四点形$ABCP$のPoncelet点を$T$とする.このとき,二直線$P_AT, \ Q_BQ_C$は$A$-midline上で交わる.
$A$-midlineと直線$Q_BQ_C,Q_CQ_A$の交点をそれぞれ$J,K$とすれば,補題28より$\measuredangle Q_CTJ =\measuredangle Q_CKJ =\measuredangle Q_CQ_AP_A =\measuredangle Q_CTP_A $と計算できるため,三点$P_A,J,T$の共線が示される.$\blacksquare$
補題27において,$T,X',X,A'$を通る円は$P_AT \cap Q_BQ_C$を通る.
三角形$ABC$と点$P$について,$P$のcevian triangleを$P_AP_BP_C$,四点形$ABCP$のPoncelet点を$T$とし,線分$BC$の中点を$M_A$とする.このとき,$\measuredangle(M_AT, P_BP_C) = \measuredangle (TP_A,BC)$が成り立つ.
$\measuredangle(M_AT, TP_A) = \measuredangle (P_BP_C,BC)$を示す.三角形$ABC$の外心を$O$とし,$A$から直線$BC$に下ろした垂線の足を$A'$とする.このとき,補題27,29から$\measuredangle M_ATP_A = $$\measuredangle M_ATA'+ \measuredangle A'TP_A =$$\measuredangle OAA' - \measuredangle (Q_BQ_C,BC) $となるので$\measuredangle (P_BP_C,BC) +\measuredangle (Q_BQ_C,BC) =$$ \measuredangle OAA'$を示せばよく,これは$\measuredangle (P_BP_C,BC) +\measuredangle (Q_BQ_C,BC) =$$ \measuredangle P_CP_BA -\angle C + \measuredangle Q_BQ_CA + \angle B =$$ \measuredangle OAA' $と計算できるので示される.$\blacksquare$
三角形$ABC$と点$P$について,$P$のcevian triangleを$P_AP_BP_C$とし,四点形$ABCP$のPoncelet点を$T$とする.また,線分$BC$の中点を$M_A$とし,$L = M_AT \cap P_BP_C$とする.このとき,$L$と$T$は線分$BC$を直径とする円での反転で互いに移り合う.
$S=P_BP_C \cap BC$とすれば,補題30より$T,L,P_A,S$は共円であるので$M_AL \times M_AT = M_AP_A \times M_AS$であるが,一方cevianによる調和点列により$M_AP_A \times M_AS = M_AB^2$となるので示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,Q_AQ_BQ_C$とし,四点形$ABCP$のPoncelet点を$T$,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$とする.また,線分$BC$の中点を$M_A$とし,$D = P_BP_C \cap \overline{XYZ},\ L= P_BP_C \cap M_AT$とする.このとき,五点$D,X,Q_A,L,T$は共円である.
補題30(または補題31)より四点$X,Q_A,L,T$は共円である.また,補題27,補題29および補題30より$\measuredangle TLD = \measuredangle TP_AQ_A = \measuredangle TXD$となって四点$D,X,L,T$の共円が従うため示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,直線$P_AP$が円$P_AP_BP_C$と再び交わる点を$N_A$,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$t_Q$とする.このとき,$Q_A,N_A$における円$P_AP_BP_C$の接線と直線$P_BP_C$は$t_Q$上で共点である.
$D=t_Q \cap P_BP_C$とすれば,補題32より直線$DQ_A$が円$P_AP_BP_C$に接することが容易なAngle chaseにより証明できるので,補題26により直線$DN_A$もまた円$P_AP_BP_C$に接することが分かり示される.$\blacksquare$
補題26において,三直線$Q_AN_A,Q_BN_B,Q_CN_C$は共点であり,この点における円$P_AP_BP_C$の極線は三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixである.
四点形$P_1P_2P_3P_4$について,そのIsogonal centerを$I$とし,Poncelet点を$T$とする.このとき,直線$P_1P_4$について$I$と対称な点と直線$P_2P_3$について$I$と対称な点の中点は$T$である.
三角形$P_1P_2P_3$の外心を$O$,三角形$P_1P_2P_3$における$P_4$の等角共役点を$Q$とし,$T$を通り直線$P_2P_3$に垂直な直線が直線$P_1P_4, \ OI$と交わる点をそれぞれ$U,V$とする.このとき,$Q$と$I$が円$P_1P_2P_3$における反転で移り合う(補題15の証明にて見たもの)ことから,$\measuredangle VIP_1 = \measuredangle QP_1O = \measuredangle(\perp P_2P_3, P_1P_4)=\measuredangle VUP_1 $となって四点$P_1,I,U,V$の共円が従う.一方$T$は三角形$P_1P_2P_3$における直線$OQ$の orthopole であるから$P_1V \perp OI$となって,$U$が$I$から直線$P_1P_4$に下ろした垂線の足であると分かる.同様に,$T$を通り$P_1P_4$に垂直な直線と$I$から直線$P_2P_3$に下ろした垂線の足を通ることが分かり,特に中点連結定理により直線$P_1P_4$について$I$と対称な点と直線$P_2P_3$について$I$と対称な点の中点が$T$であることが示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$Q$のcevian triangleを$Q_AQ_BQ_C$とし,四点形$ABCP$のPoncelet点とIsogonal centerをそれぞれ$T,R$とする.このとき,線分$TR$の垂直二等分線は三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixである.
$P$の三角形$ABC$におけるcevian triangleを$P_AP_BP_C$,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$とし直線$P_BP_C$と直線$\overline{XYZ}$の交点を$D$,$P_A$を通り直線$\overline{XYZ}$に平行な直線が円$P_AP_BP_C$と再び交わる点を$U$とする.このとき,補題32およびReimの定理から三点$D,T,U$の共線を得る.よって補題33より内接四角形$P_AUN_AT$は調和四角形であることが分かり,$(BC,AP;TP,\overline{XYZ}) = -1$が従う.したがって補題34より$RT \perp \overline{XYZ}$が成り立つことが分かるが,一方補題25より$R$は完全四辺形$\{ Q_AQ_B,Q_CQ_A,Q_AQ_B, \overline{XYZ} \}$のSteiner線上にあるから,$T$と$R$が直線$\overline{XYZ}$について互いに対称な点であることが示される.$\blacksquare$
ここまでで第一パートです.定理35はクリティカルな主張で,色々話したいこともあるのですがこれでも定理23の証明にはまだ遠いので早速次へ行きましょう.
三角形$ABC$と二点$P,Q$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C, \ Q_AQ_BQ_C$とし,tripolarをそれぞれ$\overline{X_PY_PZ_P}, \ \overline{X_QY_QZ_Q}$とする.また,$A_1=P_BP_C \cap Q_BQ_C, $$ B_1=P_CP_A \cap Q_CQ_A, $$ C_1=P_AP_B \cap Q_AQ_B$とし,$T = \overline{X_PY_PZ_P} \cap \overline{X_QY_QZ_Q}$とする.このとき,$T$は三角形$ABC$と三角形$A_1B_1C_1$のperspectorである.
Lazare Carnotの定理より六点$P_A,P_BP_C,Q_A,Q_B,Q_C$は同一円錐曲線上に乗るので,六角形$Q_CQ_AP_AP_BQ_BP_C$にPascalの定理を適用して三直線$BC,P_CQ_B,Z_PY_Q$の共点を得る.一方三角形$A_1X_PQ_A$と三角形$AZ_PY_Q$におけるDesarguesの定理から三点$A,A_1,T$の共線が従うため示される.$\blacksquare$
三角形$ABC$と二点$P,Q$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C, Q_AQ_BQ_C$とし,$X=P_BQ_C \cap P_CQ_B, $$Y=P_CQ_A \cap P_AQ_C,$$ Z=P_AQ_B \cap P_BQ_A$とする.このとき,五点$P,Q,X,Y,Z$は共線である.
$P_C-Q_C-B$と$P_B-Q_B-C$にPappusの定理を適用することで$X,P,Q$の共線が従い,同様に$Y,Z$が直線$PQ$に乗ることが示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C, \ Q_AQ_BQ_C$とし,tripolarをそれぞれ$\overline{X_PY_PZ_P}, \ \overline{X_QY_QZ_Q}$とする.このとき,$T = \overline{X_PY_PZ_P} \cap \overline{X_QY_QZ_Q}$は円$P_AP_BP_C$における直線$PQ$の極である.
$A_2=P_BQ_C \cap P_CQ_B,$$ B_2=P_CQ_A \cap P_AQ_C, $$C_2=P_AQ_B \cap P_BQ_A$とすれば,補題37より$P,Q,A_2,B_2,C_2$は共線であり,さらに補題36より$T$は円$P_AP_BP_C$における直線$\overline{A_2B_2C_2}$の極であるため示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C, \ Q_AQ_BQ_C$とし,$P,Q$のMiquel associateをそれぞれ$K_P,K_Q$とする.円$P_AP_BP_C$の中心を$O$とするとき,$OK_P = OK_Q$が成り立つ.
三角形$ABC$における$K_P$の等角共役点を$K_Q^*$とし,
直線$BC$上の点$Q_A^*$を$\angle K_PP_AQ_A^* = \angle P_AQ_A^*K_Q^*$となるように,
直線$CA$上の点$Q_B^*$を$\angle K_PP_BQ_B^* = \angle P_BQ_B^*K_Q^*$となるように,
直線$AB$上の点$Q_C^*$を$\angle K_PP_CQ_C^* = \angle P_CQ_C^*K_Q^*$となるようにそれぞれ取る.
また,$O$から直線$BC,CA,AB$に下ろした垂線の足をそれぞれ$X,Y,Z$とし,直線$K_QQ_A,K_QQ_B,K_QQ_C$上の点$U,V,W$をそれぞれ$UK_P \parallel BC,$$VK_P \parallel CA,$$WK_P \parallel AB$となるように取る.このとき$\measuredangle AP_BP_C =$$\measuredangle AK_PP_C =$$\measuredangle Q_B^*K_Q^*A =$$\measuredangle Q_B^*Q_C^*A$より四点$P_B,P_C,Q_B^*,Q_C^*$は共円であり,同様に四点$P_C,P_A,Q_C^*,Q_A^*$および$P_A,P_B,Q_A^*,Q_B^*$の共円が従うため特に六点$P_A,P_B,P_C,Q_A^*,Q_B^*,Q_C^*$の共円が従い,$Q_A^*=Q_A, $$Q_B^*=Q_B,$$Q_C^*=Q_C, $$K_Q^*=K_Q$を得る.
今,$\{ P_AK_P, Q_AK_Q \},$$\{ P_AK_P, Q_AK_Q \},$$\{ P_AK_P, Q_AK_Q \}$はそれぞれ直線$OX,OY,OZ$について対称なので,$\measuredangle K_QUK_P =$$\measuredangle K_QVK_P =$$\measuredangle K_QWK_P $となって五点$K_P,K_Q,U,V,W$の共円が従う.よって,$O$が線分$K_PU,K_PV,K_PW$の垂直二等分線上にあることから$O$がこの円の中心であると分かり,特に$OK_P=OK_Q$が示される.$\blacksquare$
$P_AK_P \cap Q_AK_Q,$$P_BK_P \cap Q_BK_Q,$$P_CK_P \cap Q_CK_Q$はすべて円$K_POK_Q$上にある.
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C, \ Q_AQ_BQ_C$とし,$P,Q$のMiquel associateをそれぞれ$K_P,K_Q$とする.円$P_AP_BP_C$の中心を$O$とするとき,直線$PQ$は円$K_POK_Q$と円$P_AP_BP_C$の根軸である.
内接四角形$P_BP_CQ_CQ_B$のMiquel点を$A'$とすれば,Brocardの定理より$AA' \perp OA'$であるから,補題39の結果と併せて$O$が円$A'K_PK_Q$における弧$K_PK_Q$の中点であると分かる.一方今$O$が円$A'P_BQ_C$および円$A'P_CQ_B$上にあることが容易に確かめられるので,三直線$P_BQ_C,P_CQ_B,OA'$三円$A'P_BQ_C,A'P_CQ_B,P_AP_BP_C$の根心で交わることが分かる.よって$A_r=P_BQ_C \cap P_CQ_B,$$ B_r=P_CQ_A \cap P_AQ_C, $$C_r=P_AQ_B \cap P_BQ_A$とすればこれら三点は円$K_POK_Q$と円$P_AP_BP_C$の根軸に乗ることが分かるが,一方補題37より直線$\overline{A_rB_rC_r}$は直線$PQ$に等しいため示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C, \ Q_AQ_BQ_C$とし,tripolarをそれぞれ$\overline{X_PY_PZ_P}, \ \overline{X_QY_QZ_Q}$,$P,Q$のMiquel associateをそれぞれ$K_P,K_Q$とする.$T = \overline{X_PY_PZ_P} \cap \overline{X_QY_QZ_Q}$とし,円$P_AP_BP_C$の中心$O$から直線$\overline{X_PY_PZ_P}, \overline{X_QY_QZ_Q}$に下ろした垂線の足をそれぞれ$U,V$とするとき,六点$K_P,K_Q,O,U,V,T$は共円である.
$T$が円$K_POK_Q$における$O$の対蹠点であることを示せばよいが,これは補題38および補題40から明らかである.$\blacksquare$
三角形$ABC$と点$P$について,そのcevian triangleを$P_AP_BP_C$とし,$P$のtripolarを$\overline{X_PY_PZ_P}$,$P$のMiquel associateを$K_P$とする.円$P_AP_BP_C$の中心$O$から直線$\overline{X_PY_PZ_P}$に下ろした垂線の足を$U$とするとき,三円$K_PP_AX_P,K_PP_BY_P,K_PP_CZ_P$は$U$で交わる.
$P$のcyclocevian conjugateを$Q$とし,$Q$のcevian triangleを$Q_AQ_BQ_C$,$Q$のMiquel associateを$K_Q$とする.このとき,補題39より$\measuredangle K_QQ_AP_A = \measuredangle OK_PK_Q +90^\circ$が成り立つから補題41より四点$K_P,P_A,X_P,U$の共円が従う.同様に,四点$K_P,P_B,Y_P,U$および$K_P,P_C,Z_P,U$の共円も従うため示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,直線$P_AP,P_BP,P_CP$が円$P_AP_BP_C$と再び交わる点をそれぞれ$N_A,N_B,N_C$,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$,$P$のMiquel associateを$K_P$とする.円$P_AP_BP_C$の中心$O$から直線$\overline{XYZ}$に下ろした垂線の足を$U$とするとき,五点の組$\{ U,X,P_A,K_P,N_A \},$$\{ U,Y,P_B,K_P,N_B \},$$\{ U,Z,P_C,K_P,N_C \}$はそれぞれ共円である.
$D=P_BP_C \cap \overline{XYZ}$とすれば,補題33より$D,N_A,O,Q_A,U$は共円であるので,$\measuredangle N_AUX =$$\measuredangle N_AUD =$$\measuredangle N_AQ_AD= $$\measuredangle N_AP_AX$となって四点$N_A,P_A,U,X$の共円を得る.一方補題41および補題42から四点$K_P,P_A,U,X$の共円が従うため示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$,$P,Q$のMiquel associateをそれぞれ$K_P,K_Q$とする.円$P_AP_BP_C$の中心$O$から直線$\overline{XYZ}$に下ろした垂線の足を$U$とし,直線$\overline{XYZ}$について$K_Q$と対称な点を$L_Q$とするとき,四点$P,K_P,U,L_Q$は共線である.
補題40,補題41および補題43より円$ZP_CK_P$,円$K_POK_Q$および円$P_AP_BP_C$の根心は$P$であって,特にこれは直線$UK_P$上に乗っている.また,補題39および補題41より三点$K_P,U,L_Q$の共線が従うため目標の共線が示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$とする.円$P_AP_BP_C$の中心$O$から直線$\overline{XYZ}$に下ろした垂線の足を$U$とし,直線$AP,BP,CP$と直線$\overline{XYZ}$の交点をそれぞれ$A_1,B_1,C_1$とする.このとき,四点の組$\{ A_1,U,P_A,Q_A \}, \{ B_1,U,P_B,Q_B \}, \{ C_1,U,P_C,Q_C \}$はそれぞれ共円である.
四点$A_1,U,P_A,Q_A$の共円を示す.直線$AP$と円$P_AP_BP_C$が再び交わる点を$N_A$とすれば,補題33より$\measuredangle Q_AUO= \measuredangle OUN_A$であるから,$OU \perp \overline{XYZ}$と併せて$\measuredangle A_1P_AQ_A = \measuredangle N_AUA_1$を示せばよいが,これは補題43より明らかであるため示される.$\blacksquare$
三角形$ABC$とcyclocevian conjugateの組$(P,Q)$について,$P,Q$のcevian triangleをそれぞれ$P_AP_BP_C,\ Q_AQ_BQ_C$とし,三角形$ABC$と三角形$Q_AQ_BQ_C$のperspectrixを$\overline{XYZ}$,$Q$のMiquel associateを$K_Q$とする.円$P_AP_BP_C$の中心$O$から直線$\overline{XYZ}$に下ろした垂線の足を$U$とし,直線$\overline{XYZ}$について$K_Q$と対称な点を$L_Q$とするとき,$\measuredangle ZL_QY= \measuredangle BPC$が成り立つ.
直線$BP,CP$と直線$\overline{XYZ}$の交点をそれぞれ$B_1,C_1$とすれば,補題42および補題45より,
$\measuredangle ZL_QY=$$\measuredangle YK_QZ=$$\measuredangle YK_QU + \measuredangle UK_QZ=$$\measuredangle YQ_BU + \measuredangle UQ_CZ =$$\measuredangle YB_1P_B + \measuredangle P_CC_1Z = \measuredangle BPC$と計算できるため示される.$\blacksquare$
以上により,長い長い証明の準備が終わりました.では,定理23を証明していきましょう.久しぶりなので主張を再掲しておきます.
三角形$ABC$とその外接円上の点$P$について,$P$のcevian triangleを$DEF$とし,cyclocevian conjugateを$Q$とする.また,線分$PH$の中点を$T$とし,$Q$のMiquel associateを$K$とする.このとき,線分$TK$の長さは円$ABC$の外接円の半径に等しい.
$Q$のcevian triangleを$XYZ$とし,三角形$ABC$と三角形$XYZ$のperspectrixを$\overline{A'B'C'}$とします.また,直線$\overline{A'B'C'}$について$K$と対称な点を$L$とし,円$DEF$の中心から直線$\overline{A'B'C'}$に下ろした垂線の足を$S$とします.
今,$P$は円$ABC$上にあるので補題46より$L$は円$AB'C',BC'A',CA'B'$に乗ることが分かり,Miquelの定理より$L$は円$ABC$上にあると分かります.一方$O$は四点形$ABCP$のIsogonal center,$T$は四点形$ABCP$のPoncelet点であるので,定理35より$O$と$T$は直線$\overline{A'B'C'}$について対称な点であると分かり,特に四角形$OTKL$が等脚台形,つまり$TK=OL$となって目標の等長が示されます.$\blacksquare$
また,定理44を踏まえれば$P$のMiquel associateを$I$としたときに四点$I,P,S,L$が共線であると分かり,さらに以下のことも分かります.
直線$AK$が円$ABC$と再び交わる点を$V$としたとき,$A'$は三角形$KVL$の外心である.
全部,原題の公式解説に対応する主張がありますよね.
では,$(\bigstar)$の点の取り方に戻って残りのさまざまな主張を見ていきましょう.
新たに,直線$\overline{RXH}, \overline{YOZ}$と円$ABC$が再び交わる点をそれぞれ$U,S$とし,円$ABC$における$R$の対蹠点を$R'$,三角形$ABC$の九点円における$X$の対蹠点を$I$,円$ABC$での反転で$P$が移る先の点を$M$とします.
このとき,先ほど示した命題群から明らかに$I$は線分$HR'$の中点かつ四点$R',I,H,S$は共線であり,Menclausの定理から$I$が$R$のcomplementであることに注意しましょう.
三点$R',G,X$はこの順に共線であり,特に$R'G:GX=2:1$が成り立つ.
$H-G-O$と$R-G-I$より$G$は三角形$RHR'$の重心であるからよい.$\blacksquare$
三角形$ABC$における$R$のSteiner線は直線$OP$に直交する.
定理17の証明を思い出せば,今$R$の等角共役点は$OP$方向の無限遠点であると分かるため示される.$\blacksquare$
$I$と$M$は三角形$ABC$について互いに等角共役である.
$I$と$Q$はAntigonal conjugateの組であるから,補題14より$I$と$M$は等角共役である.$\blacksquare$
三角形$ABC$と点$P$について,$P$のcomplementの等角共役点を$Q$とし,$P$のMiquel associateを$K$とする.このとき,$K$は cevian quotient $(P / Q)$に等しい.
三角形$ABC$と等角共役点の組$(M,M')$および直線$MM'$上の点$P$について,$P$の等角共役点と$M$およびcevian quotient$(P/M) $は共線である.
Property of Cevian quotient (post #3, #4)を見よ.
三点$R,M,I$は共線である.
$R$の等角共役点は$OP$方向の無限遠点であったから,命題50および補題51,補題52より$R$は直線$MI$上の点である他ない.$\blacksquare$
六点$O,M,X,S,U,I$は共円である.
五点$O,X,S,U,I$は明らかに共円である.また,四点$Y,R,M,O$は共円であるから,命題53より$\measuredangle OMI=$$\measuredangle OMR=$$\measuredangle OYR=$$\measuredangle OSI$となって示される.$\blacksquare$
三点$U,S,P$は共線である.
四点$U,P,Q,X$は共円である.
四点$I,M,P,Q$は共円である.
また,次のことが成り立ちます.
$J_Q = BC \cap Q_BQ_C$とする.このとき,$\triangle YAZ \overset{+}{\sim} \triangle YRJ_Q$が成り立つ.
定理47より$\triangle YAR \overset{+}{\sim} \triangle YZJ_Q$が成り立つのでよい.$\blacksquare$
直線$AZ$と直線$J_QR$は円$ABC$上で交わる.
命題55より明らか.$\blacksquare$
$J_P= BC \cap EF$とする.このとき,直線$AK$と直線$J_PR$は円$ABC$上で交わる.
定理9と全く同様にやればよい.$\blacksquare$
この命題56と命題57は単体ではあまり面白くないかもしれませんが,OMCG002(L)において$P=Q$の場合を問われていることを考えると意外と大事な感じがします.
ここからは,もっと革新的な主張を見ていきます.ラストスパートですね.
三角形$ABC$における$Y$のSteiner線は直線$QH$である.
六点$A,B,C,H,Q,R$を通る直角双曲線$\mathcal{H}_Q$に対して補題3を適用すればよい.$\blacksquare$
八点$A,B,C,I,M,S,K,Z$は同一円錐曲線上にある.
直線$QH$と直線$RI$は平行であるので,直線$RI$の等角共役を$\mathcal{H}$とすれば命題58の結果と併せて$A,B,C,I,M,S,K \in \mathcal{H}$が分かる.また,直線$SY,IQ$が$\mathcal{H}$と再び交わる点をそれぞれ$Z_1,Z_2$とし,円$ABC$を$\Gamma$とすれば,$( A,B ;C ,Z_1 )_\mathcal{H} \overset{S}{=}$$(A ,B ;C ,Y )_\Gamma \overset{R}{=}$$( A,B ;C ,Q )_{\mathcal{H}_Q} \overset{Q}{=}$$( A,B ;C ,Z_2 )_\mathcal{H} $となって$Z=Z_1=Z_2$が従うため示される.$\blacksquare$
中心を$O$とする直角双曲線$\mathcal{H}$とその直径$XY$を取り,さらに$\mathcal{H}$上に点$P$を取る.このとき,$\mathcal{H}$の$P$における接線は三角形$PXY$の$P$-Symmedianである.
$O$について$P$と対称な点を$P'$としたとき,三角形$PXY$における$P'$の等角共役点は明らかに円$PXY$の$X,Y$における接線の交点なのでよい.$\blacksquare$
$M$について$R$と対称な点を$W$とする.このとき,四点$W,H,U,I$は共円である.
$R$から四点$M,X,U,I$を通る円への方べきを二倍すればよい.$\blacksquare$
直線$WH$は直角双曲線$\mathcal{H}_Q$に接する.
$R'W \parallel OM$であるから
$\measuredangle IR'W=$$\measuredangle IR'R+ \measuredangle RR'W=$$\measuredangle YRO+ \measuredangle ROM=$$\measuredangle RPO=$$\measuredangle R'RI$と計算でき,$IR'^2 = IW \times IR$が従う.よって$I$は線分$HR'$の中点であるから$\measuredangle IHW =$$\measuredangle HRI=$$\measuredangle RHQ$が成り立つ.したがって,直角双曲線$\mathcal{H}_Q$の直径$QI$と点$H$に補題60を適用することで直線$WH$が$\mathcal{H}_Q$に接することが示される.$\blacksquare$
$W$は$Z$の三角形$ABC$における等角共役点である.
直線$UW$が円$ABC$と再び交わる点を$J$とする.このとき,命題61などから$\measuredangle JUR=$$\measuredangle WUH=$$\measuredangle WIH=$$\measuredangle MIS=$$\measuredangle MOS=$$\measuredangle (PO,OZ)$と計算できるため,命題49より三角形$ABC$における$J$のSteiner線が直線$OZ$に直交していることが分かる.よって直線$OZ$の等角共役で定まる直角双曲線を$\mathcal{H}_Z$とすれば,$J$は$\mathcal{H}_Z$と円$ABC$の第四交点である.一方命題62より直線$WH$は直線$\mathcal{H}_Q$に接しているから,補題3より$U$が三角形$ABC$における直線$WH$の反Steiner点であると分かり,再び補題3により$W$が直角双曲線$\mathcal{H}_Z$上の点であることが従う.よって補題59の結果と併せて$W$は$Z$の等角共役点であることが示される.$\blacksquare$
さて,命題63をもってこのOMCG002(L)の拡張の考察を以上とします.ここまでくるともはややりすぎですね.$P$と$Q$が一致するという条件一つだけで$Z$が類似重心$K$に等しいことが即座に分かってしまいます.
最後に
ここまで読んでくれる方がいるとは思えませんが,最後にコメントを.
もともと一日で書き終えて投稿しようくらいの気持ちでこの記事を書き始めましたが,拡張を考え始めると突然難易度が跳ね上がり驚きました.しかし,久しぶりに一日中GeoGebraを睨み続けるような日々と,脳が燃えるほどの苦悩と,声が出てしまうほどのひらめき/発見ができて最高に楽しかったです.また,個人的にとても幾何の勉強になったなと感じます.
改めて,このOMCG002(L)という素晴らしい問題を与えてくれた京都大学作問サークルおよびWriterのWasab1に感謝します.
相変わらず表記ブレブレの拙い記事ですが,ここら辺でしまいにしようと思います.
以上です.
