Skyrmionがフェルミオンである理由
SkyrmionはWess-Zumino-Witten項(WZW項)
\begin{align}
\Gamma_{WZ}&=\frac{-iN_c}{240\pi^2}
\int_{D_5^+}d^5 x \
\epsilon^{\mu\nu\alpha\beta\gamma}
{\rm tr}(L_\mu L_\nu L_\alpha L_\beta L_\gamma),\\
L_\mu &:=U^\dagger \partial_\mu U
\end{align}
と深い関係をもちます。Skyrme模型・非線形シグマ模型に量子アノマリーの効果を取り入れるにはWZW項が必要です。QCDのアノマリーによるメソンの崩壊過程は、WZW項によりこれらの模型に取り入れられますMathlog1。またSkyrme模型のトポロジカル不変量がバリオン荷であることは、WZW項のゲージ化を通じて理解できますMathlog1。
ところでSkyrmionが核子であるというなら、それはフェルミオンであるはずです。ここでフェルミオンとは空間の$2\pi$回転に対して状態・波動関数に$e^{i\pi}=-1$の位相がつくオブジェクトのことです。しかしSkyrmionはボソンのソリトンです。有限個のボソンからフェルミオンを作ることは不可能なので、Skyrmionもフェルミオンになることはないように思えます。ところが本記事で示すように、Wess-Zumino-Witten項を通じてSkyrmionがフェルミオンであることがわかります。
以下の説明はRef.Zahed1986に則していますが、この議論はWittenの論文Witten1983Bに基づいています。Skyrme模型、WZW項の基礎に関してはMathlog記事Mathlog2Mathlog3Mathlog1をご参照ください。
$2\pi$回転に対するWess-Zumino-Witten項の位相への寄与
次の問題を考えます：
Skyrmionが以下の2つの状況にある場合を考えます。
(a) 時刻$t=0$から$T$までSkyrmionが静止している
(b) $t=0$から$T$まで、Skyrmionが非常にゆっくり（＝断熱的に）一周回転する
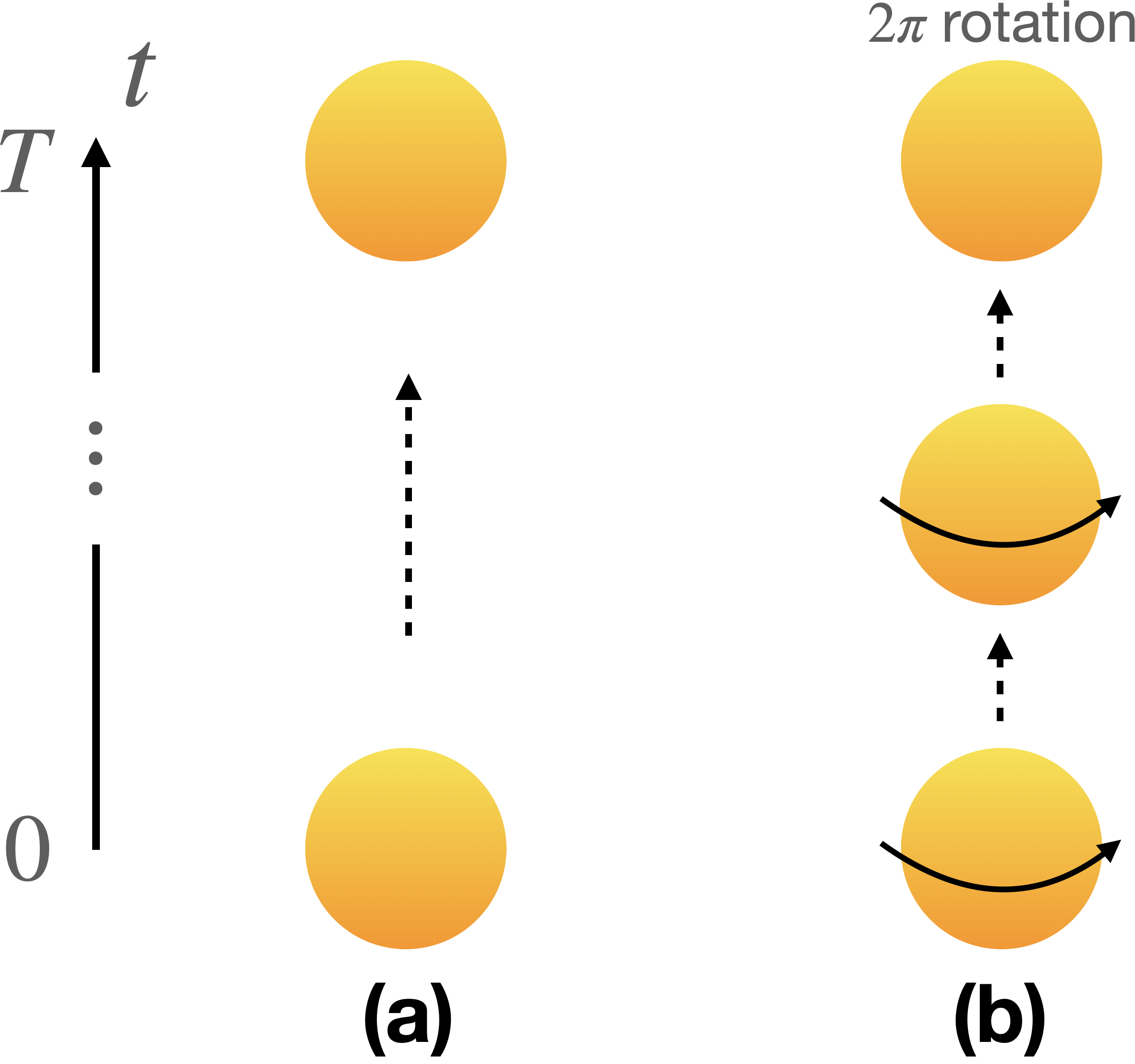過程(a)と(b)の図
このとき両者の状態にはどのような位相がつくか？
(a)は簡単で、Skyrmionの質量（エネルギー）を$M$とすると、この過程に対応する作用を$\Delta S$とすると位相は
\begin{align}
\exp(i\Delta S) =\exp(-iMT)
\end{align}
となります。
次に(b)の場合を考えます。ところが、通常のSkyrme模型の作用
\begin{align}
iS=i\int d^4x\left[ -\frac{f_\pi^2}{4}{\rm tr}(L_\mu L^\mu)+\frac{1}{4}\epsilon^2{\rm tr}([L_\mu,L_\nu]^2)\right], \ \ \ L_\mu:=U^\dagger\partial_\mu U\tag{1}
\end{align}
では、(a)と(b)の過程に関して区別がつきません。なぜならEq.(1)の時間微分を含む項は時間微分の2乗の項だからです。例えばEq.(1)の第１項の時間微分を含む項の時間積分は
\begin{align}
-\frac{f_\pi^2}{4}i\int_0^T dt\ {\rm tr}(L_0 L^0) =\frac{f_\pi^2}{4}i\int_0^T dt\ {\rm tr}\left(\frac{\partial}{\partial t}U^\dagger \frac{\partial}{\partial t} U\right)
\end{align}
です。ここでゆっくり回転することから$U=U(\epsilon t), \ \epsilon\ll 1$とします。$\tilde t=\epsilon t$と変数変換すれば
\begin{align}
=\epsilon\int_0^{\epsilon T} d\tilde t\
{\rm tr}\left(\frac{\partial}{\partial \tilde t}U^\dagger \frac{\partial}{\partial \tilde t} U\right)
\end{align}
となります。$T$を$\epsilon T$が一定になるように大きくとれば、この積分は$\epsilon\to 0$でゼロになります。
ところがWZW項は時間の微分をひとつだけ持ちます。上の議論からわかるように、時間微分が1つの項はその時間積分が$\epsilon\rightarrow 0$でも有限で残ります。つまり(a)に対する(b)の相対位相はWZW項のみからもたらされます。よって(b)の過程の位相は以下のように与えられます：
\begin{align}
\exp(i\Delta S) = \exp\left(-iMT+\frac{-iN_c}{240\pi^2}
\int_{D_5^+}d^5 x \
\epsilon^{\mu\nu\alpha\beta\gamma}
{\rm tr}(L_\mu L_\nu L_\alpha L_\beta L_\gamma)\right) \tag{2}
\end{align}
ここで$D_5^+$は境界が空間$S^3$であるような5次元の領域です（
この記事
参照のこと）。
Eq.(2)のWZW項の寄与を計算したいのですが、そのためにはSkyrme解$U$を$D_5$上に拡張しなければなりません。その際以下が重要です:
- Skyrmionの配位がflavorに関しSU(3)ならば$\pi_5(SU(3))\sim \pi_5(S^5)={\mathbb Z}$でありWZW項はノンゼロだが、SU(2)だと$\pi_5(S^3)={\bf 1}$なのでWZW項はゼロになる。よってSU(3)で考えなければならない。
- Skyrmionでは空間の回転はアイソスピン空間の回転に相当する（Skyrme解は$\exp(i\vec\tau \cdot\vec{\hat n}f(r))$のように、空間とアイソスピンのベクトルの内積を含む）
- WZW項の被積分関数はexactなので、5次元への拡張の詳細に依らず、境界条件を適切に満たす連続的な$U$ならばどのように拡張してもよい
1.よりSU(3)で考えます。$U_3({\boldsymbol x})$を
\begin{align}
U_3({\boldsymbol x})
=
\begin{pmatrix}
U({\boldsymbol x}) & \\
& 1
\end{pmatrix}
, \ \ \
U({\boldsymbol x})=\cos f(r) + i\vec\tau\cdot \vec{\hat n} \sin f(r) \ \ \ \
(\hat n^i&:=x^i/r, \ \ \ \tau^i\text{はPauli行列})
\end{align}
とします。これはSU(2)のSkyrme解をSU(3)の左上に埋め込んだものです。Skyrme解に関しては
この記事
をご参照ください。
2.より、Skyrmionの空間回転をアイソスピンでの回転に焼き直します。$U_3({\boldsymbol x},t)$を
\begin{align}
U_3({\boldsymbol x},t)
&:=\begin{pmatrix}
e^{it/2} & & \\
& e^{-it/2} & \\
& & 1
\end{pmatrix}
U_3({\boldsymbol x})
\begin{pmatrix}
e^{-it/2} & & \\
& e^{it/2} & \\
& & 1
\end{pmatrix}
\end{align}
で定義します。これはアイソスピンの第3方向を軸とした回転であり、$z$軸まわりの回転と同等です。$U_3({\boldsymbol x},t)は$$t$が$0$から$2\pi$まで進むと1回転します(※脚注)。これを少し変形しておきます：
\begin{align}
U_3({\boldsymbol x,t})
=
\begin{pmatrix}
1 & & \\
& e^{-it} & \\
& & e^{it}
\end{pmatrix}
U_3({\boldsymbol x})
\begin{pmatrix}
1 & & \\
& e^{it} & \\
& & e^{-it}
\end{pmatrix}
\end{align}
次に$U$の5次元への拡張を考えます。5次元目の座標を$\rho$とすると、5次元へ拡張されたSkyrmion$\tilde U({\boldsymbol x},t, \rho)$は境界条件として
\begin{align}
\tilde U({\boldsymbol x},t, \rho=1)=U({\boldsymbol x},t)
\end{align}
を満たすようにすればよいです。改めて、${\boldsymbol x}, t,\rho$に依存する
\begin{align}
\tilde U({\boldsymbol x},t,\rho)=
A^\dagger(t,\rho)U_3({\boldsymbol x})A(t,\rho)
\end{align}
を定義します。そして以下の$A(t,\rho)$を採用します：
\begin{align}
A(t,\rho)=
\begin{pmatrix}
1 & 0 & 0\\
0 & \rho e^{-it} & \sqrt{1-\rho^2}\\
0 & -\sqrt{1-\rho^2} & \rho e^{it}
\end{pmatrix}
\end{align}
ここで$\rho$は$[0,1]$の範囲のパラメータとします。$\rho$が$1$のとき通常の回転となります。$D^5_+$は$S^3\times \text{disc}$であり、disc部分が$\rho, t$で構成されます。パラメータの範囲はそれぞれ$[0,1], [0,2\pi] $となっています。これは$\rho$を動径方向、$t$を角度方向とした2次元の極座標に対応します。
![!FORMULA[58][35811360][0]及び時間と5次元目の座標から構成されるdisc](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FiT1bbeF8KEuzCfhm97lv.png?alt=media)
$S^3$及び時間と5次元目の座標から構成されるdisc
以上から
\begin{align}
&\tilde U({\boldsymbol x},t,\rho)=
A^\dagger(t,\rho)U_3({\boldsymbol x})A(t,\rho),\\
&U_3({\boldsymbol x})
=
\begin{pmatrix}
U({\boldsymbol x}) & \\
& 1
\end{pmatrix}
, \ \ \
U({\boldsymbol x})=\cos f(r) + i\vec\tau\cdot \vec{\hat n} \sin f(r),\\
&A(t,\rho)=
\begin{pmatrix}
1 & 0 & 0\\
0 & \rho e^{-it} & \sqrt{1-\rho^2}\\
0 & -\sqrt{1-\rho^2} & \rho e^{it}
\end{pmatrix}
\end{align}
として、計算すべき量は
\begin{align}
\Gamma_{WZ}(t=2\pi):=\frac{-iN_c}{240\pi^2}
\int_0^1 d\rho \int_0^{2\pi} dt
\int d^3x \ \epsilon^{\alpha\beta\gamma\mu\nu}
{\rm tr}(\tilde L_\alpha\tilde L_\beta\tilde L_\gamma\tilde L_\mu\tilde L_\nu), \ \ \ \
\tilde L_\mu:=\tilde U^\dagger\partial_\mu \tilde U
\tag{3}
\end{align}
です。このとき状態につく位相は$\exp(i\Gamma_{WZ}(t=2\pi))$です。
具体的な計算
Eq.(3)の積分は以下のようになります：
$\Gamma_{WZ}(t=2\pi)$は以下で与えられる：
\begin{align}
\hspace{1cm}\Gamma_{WZ}(t=2\pi)=BN_c \pi
\end{align}
ここで$N_c$はQCDにおけるカラー数、$B$はバリオン数（整数）であり
\begin{align}
B=\int d^3x (-\frac{1}{2\pi^2r^2})f'\sin^2(f)
\end{align}
である。
$\alpha,\beta,\gamma,\mu,\nu$は$\epsilon^{\alpha\beta\gamma\mu\nu}$の完全反対称性より$x,y,z,t,\rho$のいづれかである。ここで$i,j$を$\rho,t$、$a,b,c$を空間のインデックスとする。そして$\epsilon^{\alpha\beta\gamma\mu\nu}$を$\epsilon^{ij}$と$\epsilon^{abc}$に分離すると
\begin{align}
\epsilon^{\alpha\beta\gamma\mu\nu}
{\rm tr}(\tilde L_\alpha\tilde L_\beta\tilde L_\gamma\tilde L_\mu\tilde L_\nu)
=5\epsilon^{ij}\epsilon^{abc}
{\rm tr}(\tilde L_i\tilde L_j\tilde L_a\tilde L_b\tilde L_c)
\end{align}
となる（Appendix参照）。これは
\begin{align}
5\epsilon^{ij}\epsilon^{abc}{\rm tr}(\tilde L_i \tilde L_j \tilde L_a \tilde L_b \tilde L_c)
=5\epsilon^{ij}\epsilon^{abc}
{\rm tr}(\tilde L_i\tilde L_j
A^\dagger
U_3^\dagger \partial_a U_3
U_3^\dagger \partial_b U_3
U_3^\dagger \partial_c U_3
A)\tag{4}
\end{align}
と書けるが、このうち$S^3$部分の$\epsilon^{abc}U_3^\dagger \partial_a U_3
U_3^\dagger \partial_b U_3
U_3^\dagger \partial_c U_3
$は（がんばって）計算すると以下のようになる：
\begin{align}
\epsilon^{abc}U_3^\dagger \partial_a U_3
U_3^\dagger \partial_b U_3
U_3^\dagger \partial_c U_3
=
\frac{6}{r^2}\sin^2(f)f'
\begin{pmatrix}
\displaystyle {\bf 1}_{2\times 2} & \\
& \displaystyle 0
\end{pmatrix}
, \ \ \ f':=\partial_r f
\end{align}
${\bf 1}_{2\times 2}$は$2\times 2$の単位行列。以上より
\begin{align}
{\rm Eq.}(4)=\frac{30}{r^2}\sin^2(f)f' \epsilon^{ij}
{\rm tr}(A\tilde L_i \tilde L_j A^\dagger l_2), \ \ \ \
l_2:=\begin{pmatrix}
{\bf 1}_{2\times 2} & \\
& 0
\end{pmatrix}
\end{align}
である。これは
\begin{align}
=\frac{30}{r^2}\sin^2(f)f'\{-2\epsilon^{ij}{\rm tr}((\partial_iA\partial_jA^\dagger)l_2)
-\epsilon^{ij}{\rm tr}((U_3^\dagger A\partial_iA^\dagger U_3 A\partial_jA^\dagger
+A\partial_iA^\dagger U^\dagger_3A\partial_jA^\dagger U_3)l_2)\}\tag{5}
\end{align}
となる。Eq.(5)の第１項は
\begin{align}
\frac{30}{r^2}\sin^2(f)f'\{-2\epsilon^{ij}{\rm tr}((\partial_iA\partial_jA^\dagger)l_2)\}=-\frac{120}{r^2}i\rho\sin^2(f)f'
\end{align}
第２項は
\begin{align}
\frac{30}{r^2}\sin^2(f)f'\{
-\epsilon^{ij}{\rm tr}((U_3^\dagger A\partial_iA^\dagger U_3 A\partial_jA^\dagger
+A\partial_iA^\dagger U^\dagger_3A\partial_jA^\dagger U_3)l_2)\}=\frac{120}{r^2}i\rho\sin^2(f)\cos(f)f'
\end{align}
である。ここで第2項の積分への寄与は、以下のようにゼロである：
\begin{align}
\int d^3x \frac{120}{r^2}i\rho\sin^2(f)\cos(f)f'
&\propto\int_0^\infty dr \sin^2(f)\cos(f)f'\\
&\propto \int_0^\infty dr \frac{d}{dr}\sin^3(f)\\
&=\sin^3(f(r=\infty))-\sin^3(f(r=0))\\
&=0 \ \ \ \ (\because f(\infty)=0,\ f(0)=n\pi \ (n\in {\mathbb N}))
\end{align}
ゆえにWZW項Eq.(1)はEq.(5)の第１項からもたらされる：
\begin{align}
\frac{-iN_c}{240\pi^2}
\int_0^1 d\rho \int_0^{2\pi} dt
\int d^3x \epsilon^{\alpha\beta\gamma\mu\nu}
{\rm tr}(\tilde L_\alpha\tilde L_\beta\tilde L_\gamma\tilde L_\mu\tilde L_\nu)
=\frac{-iN_c}{240\pi^2}\int_0^1d\rho \int_0^{2\pi}dt\int d^3x
\ \left(-\frac{120i\rho}{r^2}\sin^2(f)f'\right)\tag{6}
\end{align}
ここでSkyrmionのバリオン数$B$は
この記事
より
\begin{align}
B=\int d^3x (-\frac{1}{2\pi^2r^2})f'\sin^2(f)
\end{align}
である。$B$を使ってEq.(6)を整理すれば、最終的に
\begin{align}
{\rm Eq.(6)}&=\frac{N_c}{240\pi^2}\times 240\pi^2B\int_0^1d\rho \ \rho \int_0^{2\pi}dt \\
&=BN_c \pi
\end{align}
を得る。${}_\blacksquare$
カラー数と統計性の関係
ということで、断熱的な$2\pi$回転によりもたらされる(a)との相対位相は
\begin{align}
\exp(i\Gamma_{WZ}(t=2\pi))=\exp(iN_c\pi B)
\end{align}
となります。
核子は$B=1$であるので、$N_c$が奇数ならフェルミオン（$\exp(i\pi)=-1$の位相がつく）、偶数ならボソン（位相はつかない）になることがわかります。現実は$N_c=3$なのでSkyrmionはフェルミオンとなり、「Skyrmion=核子」の描像と整合的です。前の記事で、WZW項の係数が$N_c$であれば、Skyrme模型・非線形シグマ模型がQCDの低エネルギー有効理論として整合的になることを述べましたMathlog1。そして本記事の例でもまたその整合性が確認できます。
まとめ
本記事ではSkyrmionがフェルミオンであることを示しました。断熱的なSkyrmionの空間$2\pi$回転に関する位相はWess-Zumino-Witten項のみからもたらされます。その位相を計算すると、$N_c$が奇数ならSkyrmionはフェルミオン、偶数ならボソンとなることがわかります。このように、WZW項は非常に巧妙な形でSkyrmionにフェルミオンとしての性質をもたらします。
本記事ではflavorがSU(3)のSkyrmionに関して議論しました。SU(2)の場合はWZW項がゼロになるので本記事の議論を適用することはできません。これに関してはまた他の記事で書こうと思います。
おしまい。${}_\blacksquare$
(※脚注) $t=2\pi$で一周するのは、前の議論における$\epsilon T={\rm const.}$の定数を$2\pi$にした場合に対応します。このとき$\epsilon\to 0$で$T\to \infty$であり、十分ゆっくり回転していることになります。
Appendix
WZW項の被積分関数$\epsilon^{\alpha\beta\gamma\mu\nu} {\rm tr}(\tilde L_\alpha\tilde L_\beta\tilde L_\gamma\tilde L_\mu\tilde L_\nu) $は$5\epsilon^{ij}\epsilon^{abc} {\rm tr}(\tilde L_i\tilde L_j\tilde L_a\tilde L_b\tilde L_c)$になることを示します（$i,j$: $\rho,t$のインデックス、$a,b,c$:$\boldsymbol x$のインデックス）。
まず$\epsilon^{\alpha\beta\gamma\mu\nu}{\rm tr}(\cdots)$を$\epsilon^{ij}\epsilon^{abc}{\rm tr}(\cdots)$に書きなおします。このとき$\rm tr$部分は
- $\tilde L_i$と$\tilde L_j$が隣り合うものを$\rm tr$の中で巡回したもの
- $\tilde L_a$を1つはさんで$\tilde L_i$と$\tilde L_j$が隣り合うものを$\rm tr$の中で巡回したもの
の2つの場合に分けることができます。すなわち
\begin{align}
\epsilon^{\alpha\beta\gamma\mu\nu}{\rm tr}(\tilde L_\alpha\tilde L_\beta\tilde L_\gamma\tilde L_\mu\tilde L_\nu)
&=\epsilon^{ij}\epsilon^{abc}
\Big\{
{\rm tr}(\tilde L_i\tilde L_j\tilde L_a\tilde L_b\tilde L_c)
+{\rm tr}(\tilde L_c \tilde L_i\tilde L_j\tilde L_a\tilde L_b)
+\cdots
+{\rm tr}(\tilde L_j \tilde L_a\tilde L_b\tilde L_c\tilde L_i)\\
&\hspace{1.5cm}-{\rm tr}(\tilde L_i\tilde L_a\tilde L_j\tilde L_b\tilde L_c)
-{\rm tr}(\tilde L_c L_i\tilde L_a\tilde L_j\tilde L_b)
-\cdots
-{\rm tr}(\tilde L_a \tilde L_j\tilde L_b\tilde L_c\tilde L_i)\Big\}\\
&=5\epsilon^{ij}\epsilon^{abc}
{\rm tr}(\tilde L_i\tilde L_j\tilde L_a\tilde L_b\tilde L_c)
-5\epsilon^{ij}\epsilon^{abc}{\rm tr}(\tilde L_i \tilde L_a\tilde L_j\tilde L_b\tilde L_c)
\end{align}
と書けます。ここで最後の行の第2項は（がんばって）計算するとゼロになります。
ゆえに
\begin{align}
\epsilon^{\alpha\beta\gamma\mu\nu}{\rm tr}(\tilde L_\alpha\tilde L_\beta\tilde L_\gamma\tilde L_\mu\tilde L_\nu)=5\epsilon^{ij}\epsilon^{abc}
{\rm tr}(\tilde L_i\tilde L_j\tilde L_a\tilde L_b\tilde L_c)
\end{align}
になります。${}_\blacksquare$
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
