求角問題における外心の更なる有用性 with 第5回匿式図形問題エスパー杯 (T-GUESS Cup 5) 問題Fの解説
ウェブサイト軽量化のため、一部画像の解像度を落としています。点線で囲まれた画像をクリックすると、その画像の高解像度版が新しいタブで表示されます。
挨拶は省略します。タイトルの通り、求角問題(角度に関する諸々の情報が与えられたときに、ある未知の角度を求める問題の総称)を解くにあたって外心に注目することの意義を、自作問題の解説とあわせて執筆しました。スタートとゴールだけ先にお見せするので、ここから先へ読み進めるか否かの判断材料としてください。
導入パート
初等幾何の歴史の中で、求角問題というジャンルは長きにわたり注目されてきました。特に、 ラングレーの問題 (Langley's Adventitious Angles)を端緒とする「整角四角形」という問題群は、単純ながらも2015年まで初等幾何による完全解決が得られない難問を、極めて多く含むグループでした。このあたりの歴史は以前の記事『 求角問題と外心3つ法と「外心10個法」(前編) 』にやや詳しく記しているので、本記事では核心の部分のみ記します。先にいくらか定義を述べます。
凸四角形$ABCD$において、$\angle ABD,$$\angle CBD,$$\angle ACB,$$\angle ACD$の大きさが判明しているならば、$\angle ADB$の大きさは一意に決定される。これら5つの角度がすべて(度数法で)整数値であるとき、四角形$ABCD$は整角四角形と呼ばれる。
$\triangle ABC$において、$\angle A,$$\angle B,$$\angle C$の角度がすべて(度数法で)整数値であるとき、$\triangle ABC$は整角三角形と呼ばれる。
$z=\exp\left(\dfrac{i\pi}{180}\right)$とする。整数$n$を用いて$z^n$と表せる360種類のベクトルを整角単位ベクトルと呼ぶことにする。また、整角単位ベクトルの実数倍として表せるベクトルを整角ベクトルと呼ぶことにする。つまり、偏角が${-180}^{\circ},{-179}^{\circ},\dots,{179}^{\circ}$のベクトルに便宜上名前を付与しただけである。
外心3つ法
aerile_re 氏が2015年に発表した「外心3つ法」は、整角四角形の初等的考察に終止符を打つものでした。
整角四角形$ABCD$において、$\angle ABD,$$\angle CBD,$$\angle ACB,$$\angle ACD$の大きさが判明しているならば、$\angle ADB$の大きさを初等的に求められる。
定理1を証明します。外心3つ法を用いれば、点$A$から点$D$までの経路を、長さが等しい6本のベクトルの合成に対応させられます(手順省略)。これら6本のベクトルの偏角はすべて整数値であり、合成した偏角も整数値です。ゆえに、6本のベクトルを直線$AD$で折り返せば、適当な拡大縮小により整角単位ベクトル12本で構成された閉路(始点と終点が一致する経路)が得られ、結局以下の定理2を示せばよいことになります。
整角単位ベクトル複数本で構成された経路${\boldsymbol{p}}$が閉路であるとき、${\boldsymbol{p}}$に含まれるベクトルを以下の自明な閉路の和に分割できる。
① 点対称な図形(二角形を含む)の各辺を構成するベクトル
② 正三角形の各辺を構成するベクトル
③ 正五角形(あるいは五芒星)の各辺を構成するベクトル
逆に、①・②・③の和で表せる経路は明らかに閉路である。
定理2と同値な主張が 外心3つ法発案者の記事 にて証明されているため、定理1が示されました。いきなり他力本願ですね。なお、 だま氏様の記事 でさらに詳細な計算方法が書かれており、大学数学をまともに学んだ方ならばこちらも参考になさるようお願いします。
本質の抽出
外心3つ法を軽くおさらいしましたが、その本質は何であったかを考えてみましょう。すると、「既知の偏角をもつ整角単位ベクトルで経路を構成する」ことが本質である旨を見抜けますね。ここから、次のようなモチベーションが湧いてまいります。
「同じことを、他の求角問題で使えないかな?」
このモチベーションをもとに執筆したのが、昨年7月の『
求角問題と外心3つ法と「外心10個法」(前編)
』および『
求角問題と外心3つ法と「外心10個法」(後編)
』です。これらでは、整角四角形を二段重ねたような形状の求角問題に同様のメソッドを用い、36本の整角単位ベクトルで経路メイキングを行いました。
今回の記事では、同じ本質を抱きつつ、以前とは違った方向に外心3つ法を拡張していこうと思います。以後、整角ベクトルの経路が頻出するので、利便性を考え名前を付けてあげましょう。
長さの等しい整角ベクトル$n$本で構成される経路を整角$n$等辺経路と呼ぶことにする。例えば、経路$ABCD$が整角三等辺経路であるならば「$\overrightarrow{AB},$$\overrightarrow{BC},$$\overrightarrow{CD}$の偏角が整数度であり、かつ$|\overrightarrow{AB}|$$=|\overrightarrow{BC}|$$=|\overrightarrow{CD}|$」が成立する。
外心3つ法により、$\overrightarrow{AD}$が何らかの整角六等辺経路に変換されることをご理解いただければ、次のパートに進みます。なお、$\overrightarrow{AD}$の偏角を$\arg\overrightarrow{AD}$とも表します。
紹介パート
最初の拡張
整角四角形において、対角線$AC,BD$の交点を$P$とすると、3点の組$(A,P,C),$$(B,P,D)$はいずれも同一直線上に存在します。自明ですね。
いま、この点$P$を任意に動かすことを考えましょう。すなわち、前述の共線を取り除き、図の自由度を上げるのです。そうすると、以下の問題が現れます。
凸四角形$ABCD$とその内部の点$P$において、$\triangle ABP,$$\triangle BCP,$$\triangle CDP$がすべて整角三角形をなし、その内角が既知であるとする。このとき、$\angle ADP$の大きさは一意に決定されるが、それが(度数法で)整数値であることが保証されるとき、$\angle ADP$を初等的に求めなさい。
この問題も、「既知の偏角をもつ整角$n$等辺経路を構成する」が使えます。点$A$から点$D$までに、そのようなパスウェイを設けてあげればよいです。どのように設けるかを軽く解説します。
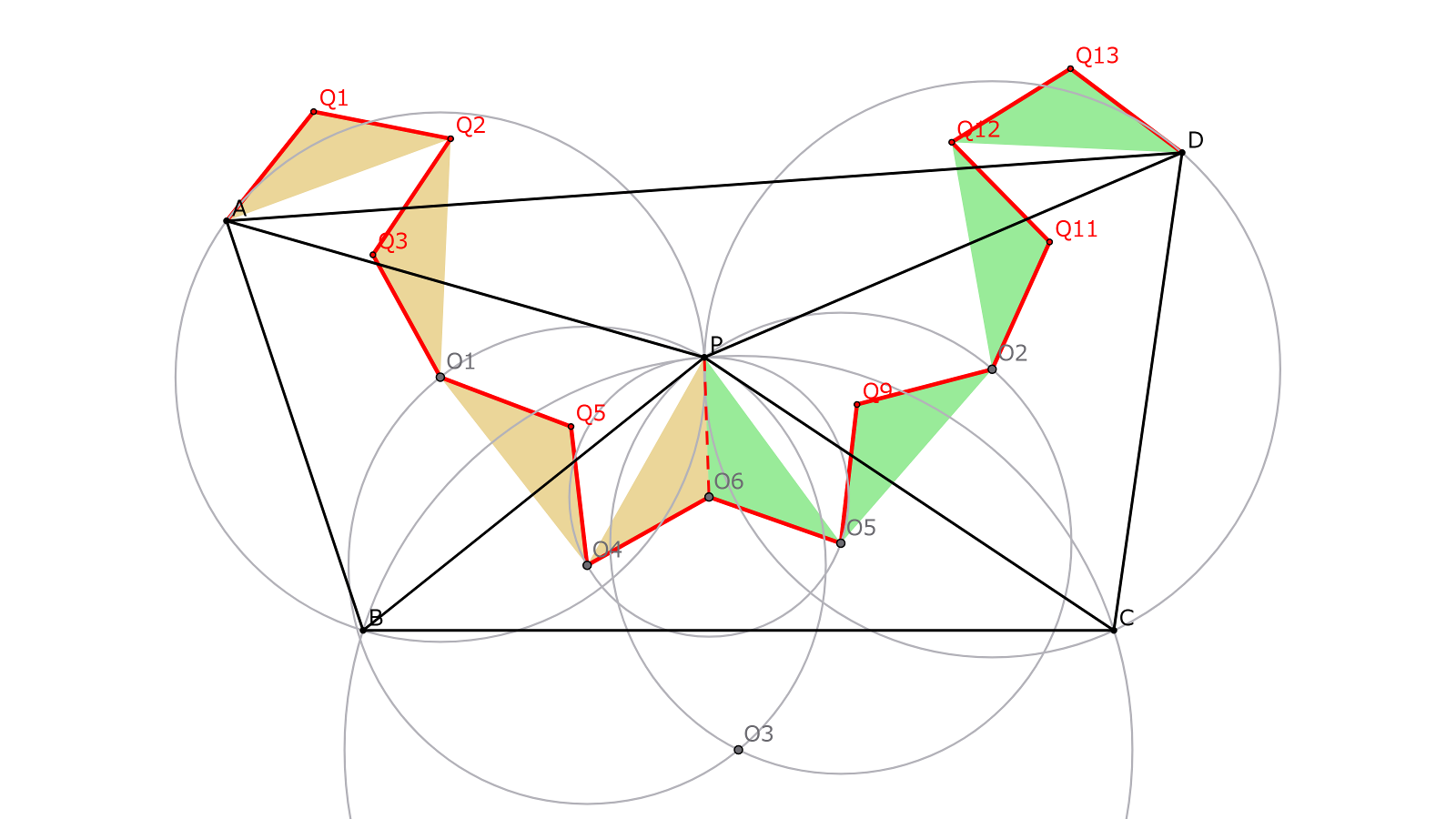
$\triangle ABP,$$\triangle CDP,$$\triangle BCP$の外心をそれぞれ$O_1,O_2,O_3$とし、$\triangle O_1O_3P,$$\triangle O_2O_3P$の外心をそれぞれ$O_4,O_5$、$\triangle O_4O_5P$の外心を$O_6$とします。$\triangle PO_1O_4 \equiv \triangle AO_1Q_2$、$\triangle PO_2O_5 \equiv \triangle DO_2Q_{12}$をみたす点$Q_2,Q_{12}$をとり、$\triangle PO_4O_6$$\equiv \triangle AQ_2Q_1$$\equiv \triangle Q_2O_1Q_3$$\equiv O_1O_4Q_5$、$\triangle PO_5O_6$$\equiv \triangle O_5O_2Q_9$$\equiv \triangle O_2Q_{12}Q_{11}$$\equiv Q_{12}DQ_{13}$をみたす点$Q_1,Q_3,$$Q_5,Q_9,$$Q_{11},Q_{13}$を拵えます(複数の拵え方が考えられますが、どう拵えても大丈夫です)。ここで$O_1=Q_4,$$O_4=Q_6,$$O_6=Q_7,$$O_5=Q_8,$$O_2=Q_{10}$と別名を付ければ、経路$AQ_1Q_2\dots Q_{13}D$が整角十四等辺経路になるのです。なぜならば、簡単な計算(まあまあ大変)から$\triangle PO_4O_6,$$\triangle PO_5O_6$は整角三角形であること、直線$BC$を基準とした6本のベクトル$\overrightarrow{AQ_2},\overrightarrow{Q_2Q_4},$$\overrightarrow{Q_4Q_6},\overrightarrow{Q_8Q_{10}},$$\overrightarrow{Q_{10}Q_{12}},\overrightarrow{Q_{12}D}$の偏角もすべて整数度になることを、各々証明できるから、ということになります。問題1は、14本の整角単位ベクトルの合成として解釈できるのですね。執筆してから気づきましたが、問題1が初等的に解ける旨は だま氏様の記事 で既に言及されております。つまりここまでは周知の事実といっても過言ではありませんね。
次なる拡張
さて、先ほどは点$P$(四角形$ABCD$の対角線の交点)に関する拡張を考えました。他に拡張できるところは無いでしょうか。色々と思考を巡らせてみます。すると、従来の外心3つ法の本質である「線分$AD$を整角単位ベクトルの合成に変換する」という発想から、次のアイデアが浮かんできます。
「四角形の他の辺を、整角$n$等辺経路に置き換えることができるかも?」
ということで、以下の問題が現れます。
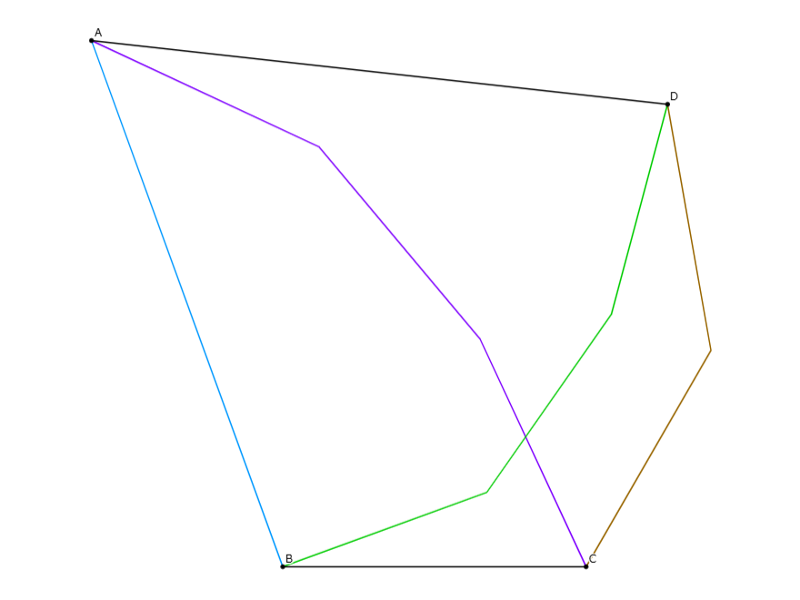
凸四角形$ABCD$において、$\overrightarrow{BC}$の偏角を$0^{\circ}$とし、整角$n_{AB}$等辺経路$A\dots B$($n_{AB}$本の等長な整角ベクトルを含む。以下同様)、整角$n_{CD}$等辺経路$C\dots D$、整角$n_{AC}$等辺経路$A\dots C$、整角$n_{BD}$等辺経路$B\dots D$が与えられる。このとき$\arg\overrightarrow{AD}$は一意に決定されるが、それが(度数法で)整数値であることが保証されるとき、$\arg\overrightarrow{AD}$を初等的に求めなさい。
この問題で外心3つ法を用いようとすると躓きます。というのも、$\triangle ABC,$$\triangle BCD$の各辺の偏角が整数度とは限らないため、外心から各頂点に向かう線分の偏角も整数値で表せない可能性が出てくるからです。整角単位ベクトルのみを含む経路でなければ定理2を用いることができません。要するに解けません。どうしましょうか。
まず考えるべきことは、$\triangle ABC$の外心$O$について$\arg\overrightarrow{OA}$を求めることです。いま、$\triangle ABC$の垂心を$H$とすれば、有名性質より$O$と$H$は$\triangle ABC$について等角共役ですから、
$$\begin{align*}
\arg\overrightarrow{OA}+\arg\overrightarrow{HA}&=\arg\overrightarrow{BA}+\arg\overrightarrow{CA} \\
\arg\overrightarrow{OA}&=\arg\overrightarrow{AB}+\arg\overrightarrow{CA}-\arg\overrightarrow{BC}\pm{90}^{\circ}
\end{align*}$$と求められます(複号は点の位置関係により変動します)。この事実をもとに、以下の重要な補題を示します。
整角$n_{AB}$等辺経路$A\dots B$、整角$n_{BC}$等辺経路$B\dots C$、整角$n_{CA}$等辺経路$C\dots A$が与えられる。$\triangle ABC$の外心を$O$としたとき、点$O$から点$A,B,C$に向かう整角$n_{AB}n_{BC}n_{CA}$等辺経路$O\dots A,$$O\dots B,$$O\dots C$であり、経路全体の長さもすべて等しいものが存在する。具体的には、
経路$O\dots A$:「「「線分$OA,AB$が重なるように経路$A\dots B$を相似拡大・回転・平行移動した経路」の各辺と$BC$がそれぞれ重なるように経路$B\dots C$の鏡像を相似拡大・回転・平行移動した経路」の各辺と$CA$がそれぞれ重なるように経路$C\dots A$を相似拡大・回転・平行移動した経路」
経路$O\dots B$:「「「線分$OA,AB$が重なるように経路$A\dots B$を相似拡大・回転・平行移動した経路」の各辺と$BC$がそれぞれ重なるように経路$B\dots C$を相似拡大・回転・平行移動した経路」の各辺と$CA$がそれぞれ重なるように経路$C\dots A$の鏡像を相似拡大・回転・平行移動した経路」
経路$O\dots C$:「「「線分$OA,AB$が重なるように経路$A\dots B$の鏡像を相似拡大・回転・平行移動した経路」の各辺と$BC$がそれぞれ重なるように経路$B\dots C$を相似拡大・回転・平行移動した経路」の各辺と$CA$がそれぞれ重なるように経路$C\dots A$を相似拡大・回転・平行移動した経路」
とすればよい。
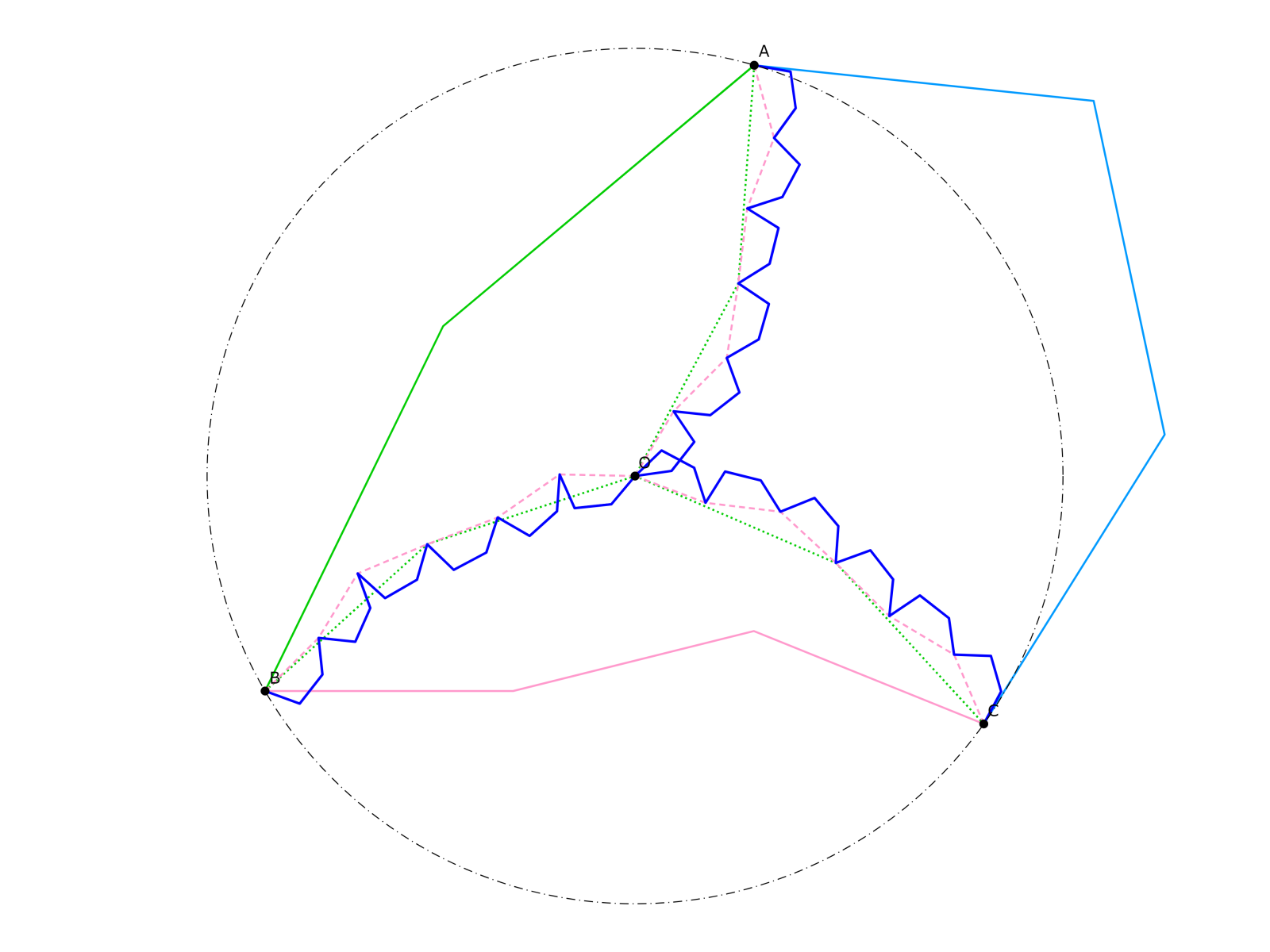
$\arg\overrightarrow{BC}=(N_a+d_a)^{\circ},$$\arg\overrightarrow{CA}=(N_b+d_b)^{\circ},$$\arg\overrightarrow{AB}=(N_c+d_c)^{\circ}$と表します(ただし$N_a,N_b,N_c$は整数、$0\le d_a<1,$$0\le d_b<1,$$0\le d_c<1$)。また、経路$A\dots B$が$A$の次に通る頂点を$A_1$、経路$B\dots C$が$B$の次に通る頂点を$B_1$、経路$C\dots A$が$C$の次に通る頂点を$C_1$と名付けます。このとき$\overrightarrow{BB_1},$$\overrightarrow{CC_1},$$\overrightarrow{AA_1}$の偏角は明らかに整数度ですから、整数$M_a,M_b,M_c$を用いて$\arg\overrightarrow{BB_1}={M_a}^{\circ},$$\arg\overrightarrow{CC_1}={M_b}^{\circ},$$\arg\overrightarrow{AA_1}={M_c}^{\circ}$と表せますね。したがって、$\measuredangle CBB_1$$=(M_a-N_a-d_a)^{\circ},$$\measuredangle ACC_1$$=(M_b-N_b-d_b)^{\circ},$$\measuredangle BAA_1$$=(M_c-N_c-d_c)^{\circ}$です($\measuredangle$は
有向角
を表す記号)。
「線分$OA,AB$が重なるように経路$A\dots B$を相似拡大・回転・平行移動した経路」を描き、$A_1$の移る点を$A_2$とします。$\measuredangle AOA_2=\measuredangle BAA_1$より、
$$\begin{align*}
\arg\overrightarrow{OA_2}&=\arg\overrightarrow{OA}+\measuredangle AOA_2 \\
&=\arg\overrightarrow{AB}+\arg\overrightarrow{CA}-\arg\overrightarrow{BC}\pm{90}^{\circ}+\measuredangle BAA_1 \\
&=(N_b+d_b)^{\circ}+(N_c+d_c)^{\circ}-(N_a+d_a)^{\circ}+(M_c-N_c-d_c)^{\circ}\pm{90}^{\circ} \\
&=(-N_a+N_b-d_a+d_b+M_c\pm{90})^{\circ}
\end{align*}$$のように計算できました。
今度は「線分$OA_2,BC$が重なるように経路$B\dots C$の鏡像を相似拡大・回転・平行移動した経路」を描き、$B_1$の移る点を$B_2$とします。$\measuredangle A_2OB_2=-\measuredangle CBB_1$より、
$$\begin{align*}
\arg\overrightarrow{OB_2}&=\arg\overrightarrow{OA_2}+\measuredangle A_2OB_2 \\
&=(N_b+d_b-M_a+M_c\pm{90})^{\circ}
\end{align*}$$です。引き続き「線分$OB_2,CA$が重なるように経路$C\dots A$を相似拡大・回転・平行移動した経路」を描き、$C_1$の移る点を$C_2$とします。$\measuredangle B_2OC_2=\measuredangle ACC_1$より、
$$\begin{align*}
\arg\overrightarrow{OC_2}&=\arg\overrightarrow{OB_2}+\measuredangle B_2OC_2 \\
&=(-M_a+M_b+M_c\pm{90})^{\circ}
\end{align*}$$ですね。もう一度言います、$\arg\overrightarrow{OC_2}$$=(-M_a+M_b+M_c\pm{90})^{\circ}$です。気づきましたね。$M_a,M_b,M_c$は整数ですから、$\overrightarrow{OC_2}$は整角ベクトルなのです。経路$O\dots A$の他のベクトルについても同様の計算を行うことで、最終的にすべてのベクトルが整角ベクトルであることを示せます。これらのベクトルの長さはいずれも明らかに等しいですね。さらに経路$O\dots B,$$O\dots C$についても同じことがいえるため、補題3の主張を確かめられました。
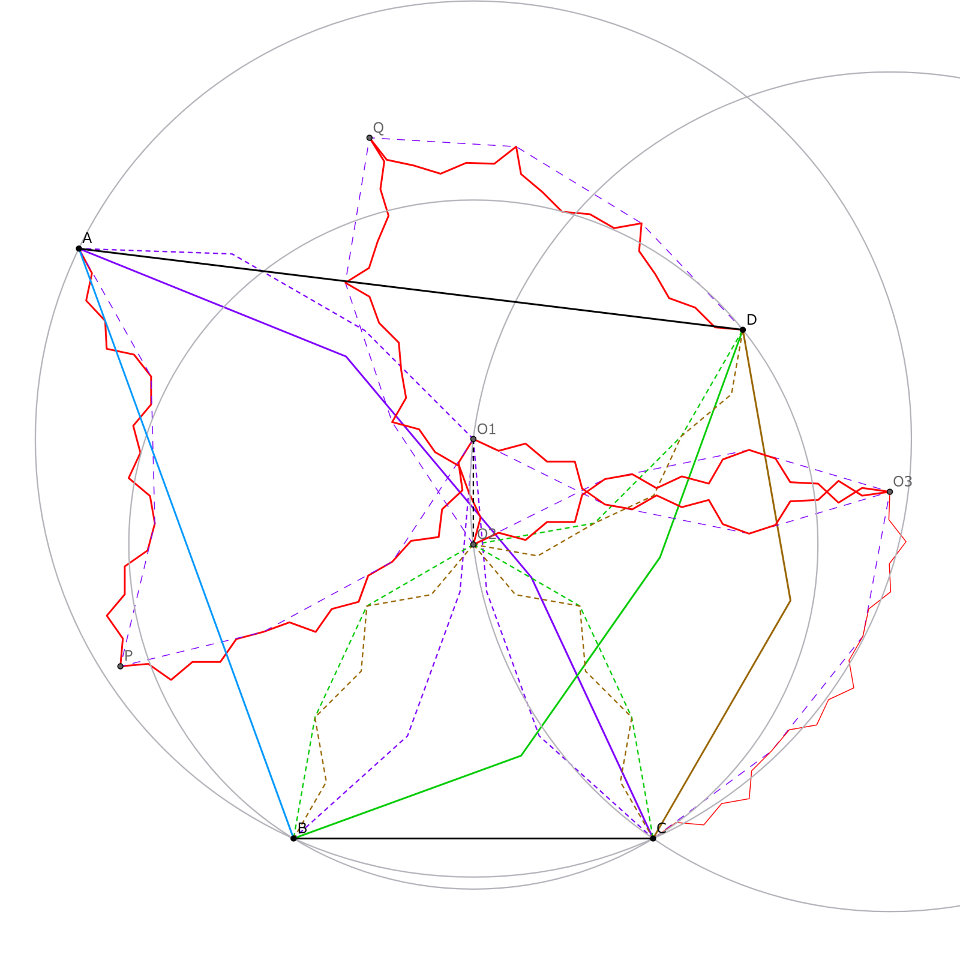
問題2に戻ります。$\triangle ABC,$$\triangle BCD$の外心を各々$O_1,O_2$とし、$\triangle O_1O_2C$の外心を$O_3$とします(外心3つ法と一緒です)。たった今証明した補題3から、点$O_1$を始点とし点$A,B,C$を終点とする整角$n_{AB}n_{AC}$等辺経路$O_1\dots A,$$O_1\dots B,$$O_1\dots C$の存在が確定します(辺$BC$を整角一等辺経路とみなしました)。同じく、点$O_2$を始点とし点$B,C,D$を終点とする整角$n_{CD}n_{BD}$等辺経路$O_2\dots B,$$O_2\dots C,$$O_2\dots D$の存在が言えますね。さらに$O_1O_2 \perp BC$より、$\triangle O_1O_2C$にも補題3を使えるのです。実際に使ってみますと、点$O_3$を始点とし点$O_1,O_2,C$を終点とする整角$n_{AB}n_{CD}n_{AC}n_{BD}$等辺経路$O_3\dots O_1,$$O_3\dots O_2$を構成できます。
$\triangle CO_3O_1$$\equiv \triangle APO_1,$$\triangle CO_3O_2$$\equiv \triangle DQO_2$となる点$P,Q$をとり、補題3を示したときと同様の議論(角度の小数部分に注目する)を行うことで、
経路$A\dots P$:「「「「線分$AP,AB$が重なるように経路$A\dots B$を相似拡大・回転・平行移動した経路」の各辺と$CD$がそれぞれ重なるように経路$C\dots D$を相似拡大・回転・平行移動した経路」の各辺と$AC$がそれぞれ重なるように経路$A\dots C$を相似拡大・回転・平行移動した経路」の各辺と$BD$がそれぞれ重なるように経路$B\dots D$の鏡像を相似拡大・回転・平行移動した経路」
経路$P\dots O_1$:「「「「線分$PO_1,AB$が重なるように経路$A\dots B$を相似拡大・回転・平行移動した経路」の各辺と$CD$がそれぞれ重なるように経路$C\dots D$の鏡像を相似拡大・回転・平行移動した経路」の各辺と$AC$がそれぞれ重なるように経路$A\dots C$を相似拡大・回転・平行移動した経路」の各辺と$BD$がそれぞれ重なるように経路$B\dots D$を相似拡大・回転・平行移動した経路」
経路$O_2\dots Q$:「「「「線分$O_2Q,AB$が重なるように経路$A\dots B$を相似拡大・回転・平行移動した経路」の各辺と$CD$がそれぞれ重なるように経路$C\dots D$を相似拡大・回転・平行移動した経路」の各辺と$AC$がそれぞれ重なるように経路$A\dots C$の鏡像を相似拡大・回転・平行移動した経路」の各辺と$BD$がそれぞれ重なるように経路$B\dots D$を相似拡大・回転・平行移動した経路」
経路$Q\dots D$:「「「「線分$O_2Q,AB$が重なるように経路$A\dots B$の鏡像を相似拡大・回転・平行移動した経路」の各辺と$CD$がそれぞれ重なるように経路$C\dots D$を相似拡大・回転・平行移動した経路」の各辺と$AC$がそれぞれ重なるように経路$A\dots C$を相似拡大・回転・平行移動した経路」の各辺と$BD$がそれぞれ重なるように経路$B\dots D$を相似拡大・回転・平行移動した経路」
がすべて整角$n_{AB}n_{CD}n_{AC}n_{BD}$等辺経路になることを簡単に計算(誰がどう考えても超大変)できます。各経路の1辺の長さは明らかに等しく、また事前に作っておいた経路$O_1\dots O_3,$$O_3\dots O_2$の1辺も同じ長さになりますから、これら6つの経路を結ぶことにより整角$6n_{AB}n_{CD}n_{AC}n_{BD}$等辺経路$A\dots P\dots O_1$$\dots O_3\dots O_2$$\dots Q\dots D$が完成します。ごり押しにも程がありますが、なんとか点$A$と点$D$を経路で結ぶことに成功し、問題2が解けました。
拡張の統合
さて。さて、整角四角形に対する2種類の拡張を初等的に解決しました。折角なので、これら2種類をうまく混ぜ合わせることができないかを考えます。いえ、考えるまでもなく、問題1に現れる各線分を経路に変えれば統合できそうですね。最終的に以下の問題となります。
凸四角形$ABCD$とその内部の点$P$において、$\overrightarrow{BC}$の偏角を$0^{\circ}$とし、整角$n_{AB}$等辺経路$A\dots B$、整角$n_{CD}$等辺経路$C\dots D$、整角$n_{AP}$等辺経路$A\dots P$、整角$n_{BP}$等辺経路$B\dots P$、整角$n_{CP}$等辺経路$C\dots P$、整角$n_{DP}$等辺経路$D\dots P$が与えられる。このとき$\arg\overrightarrow{AD}$は一意に決定されるが、それが(度数法で)整数値であることが保証されるとき、$\arg\overrightarrow{AD}$を初等的に求めなさい。
問題3の詳細な解法は記しませんが、従来の考え方をそのまま用いれば整角$14n_{AB}n_{CD}n_{AP}$$n_{BP}n_{CP}n_{DP}$等辺経路を構成できます。非人道的ですね。例えば$n_{AB}=n_{CD}$$=n_{AP}=n_{BP}$$=n_{CP}=n_{DP}$$=3$のとき($\overrightarrow{AB},\overrightarrow{CD},$$\overrightarrow{AP},\overrightarrow{BP},$$\overrightarrow{CP},\overrightarrow{DP}$の偏角がいずれも有理数度とならない可能性がある最小のケース)、$14\times 3^6=10206$より整角一万二百六等辺経路を考えることになります。これ以上はやめましょう。
問題2・問題3で、他の辺は容赦なく整角$n$等辺経路へと置換していくのに、なぜ辺$BC$はそのまま残したのか、と訝った読者がいらっしゃるかもしれません。こちらにはちゃんと理由がございます。仮に辺$BC$も整角$n_{BC}$等辺経路$B\dots C$とした場合、他の経路の各辺と$BC$がそれぞれ重なるように経路$B\dots C$をペタペタ貼りつけると、新しく描かれた経路の各辺について、$\overrightarrow{BC}$を基準としたときの偏角が整数度になるのです。すなわち、$B$から$C$まで一本線、他の辺は整角$n$等辺経路、と既に考察した事項の焼き増しにしかなりません。解ける問題の範囲が変わらないのに余計な煩雑さをもたらしてしまうため、辺$BC$だけは一切弄らなかったのですね。
実演パート
とはいえ、存在性だけ示して放置という選択は、あまりにも数学者らしすぎます(偏見)。少しは実体験を積みたいですね。そこで、問題3において$n_{AB}=n_{CD}$$=3,$$n_{AP}=n_{BP}$$=n_{CP}=n_{DP}$$=1$とした比較的易しめの問題を解いてみることにしましょう。易しめと言いつつ、工夫せずに解くと百二十六等辺百二十七角形が現れてしまうのですが……。
コンテスト
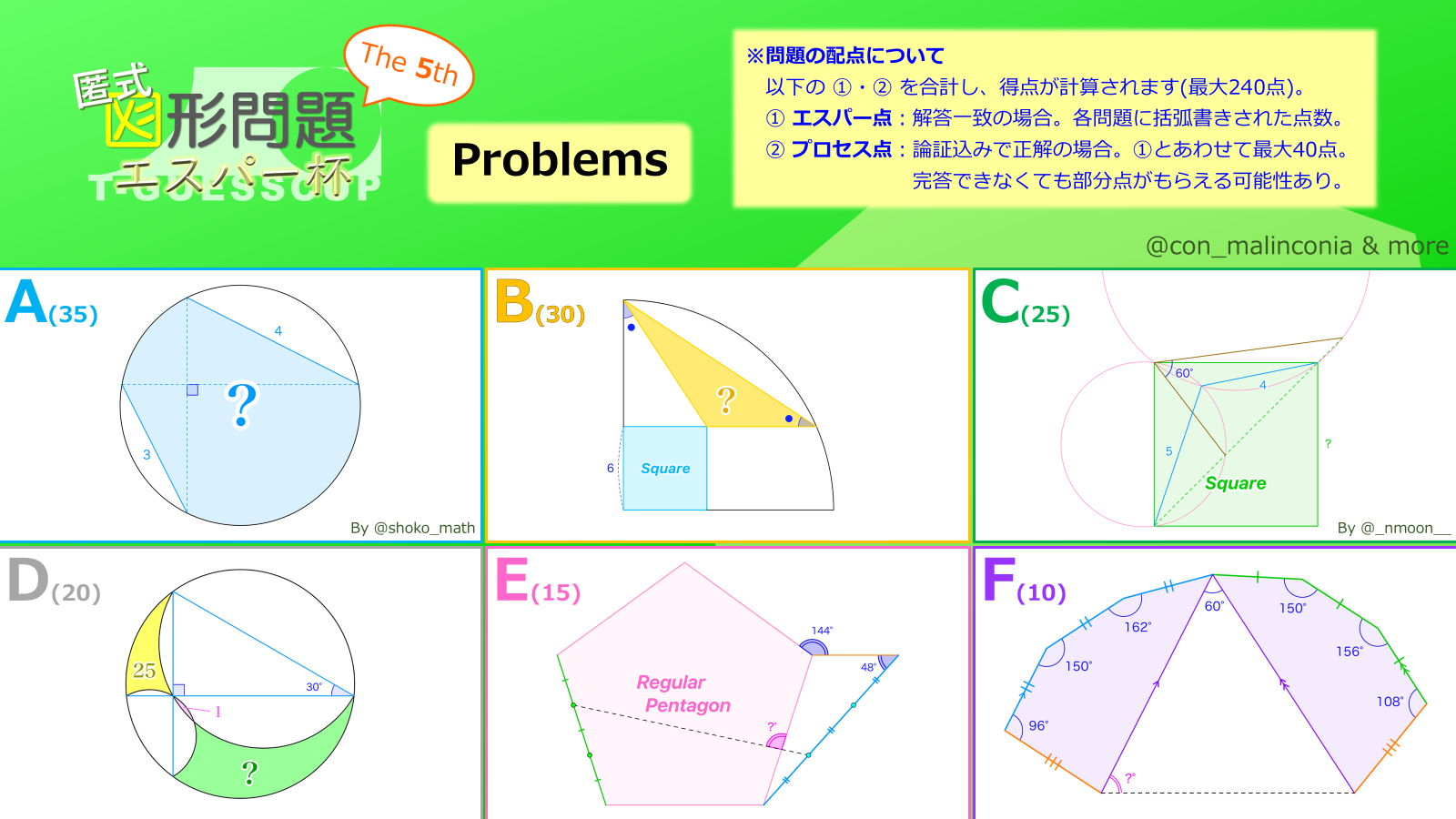
2025年5月3日~5月11日にかけて『 第5回匿式図形問題エスパー杯 (T-GUESS Cup 5: Tock's Geometry "Using Extra-Sensory Solutions" Cup The 5th)』を開催しました。ご参加くださった皆様、ありがとうございました。どうして急にコンテストの話を、とお思いかもしれませんが、当該コンテストの問題Fにて、まさに先述の「実体験」ができる問題を出したのです。それがこちら。
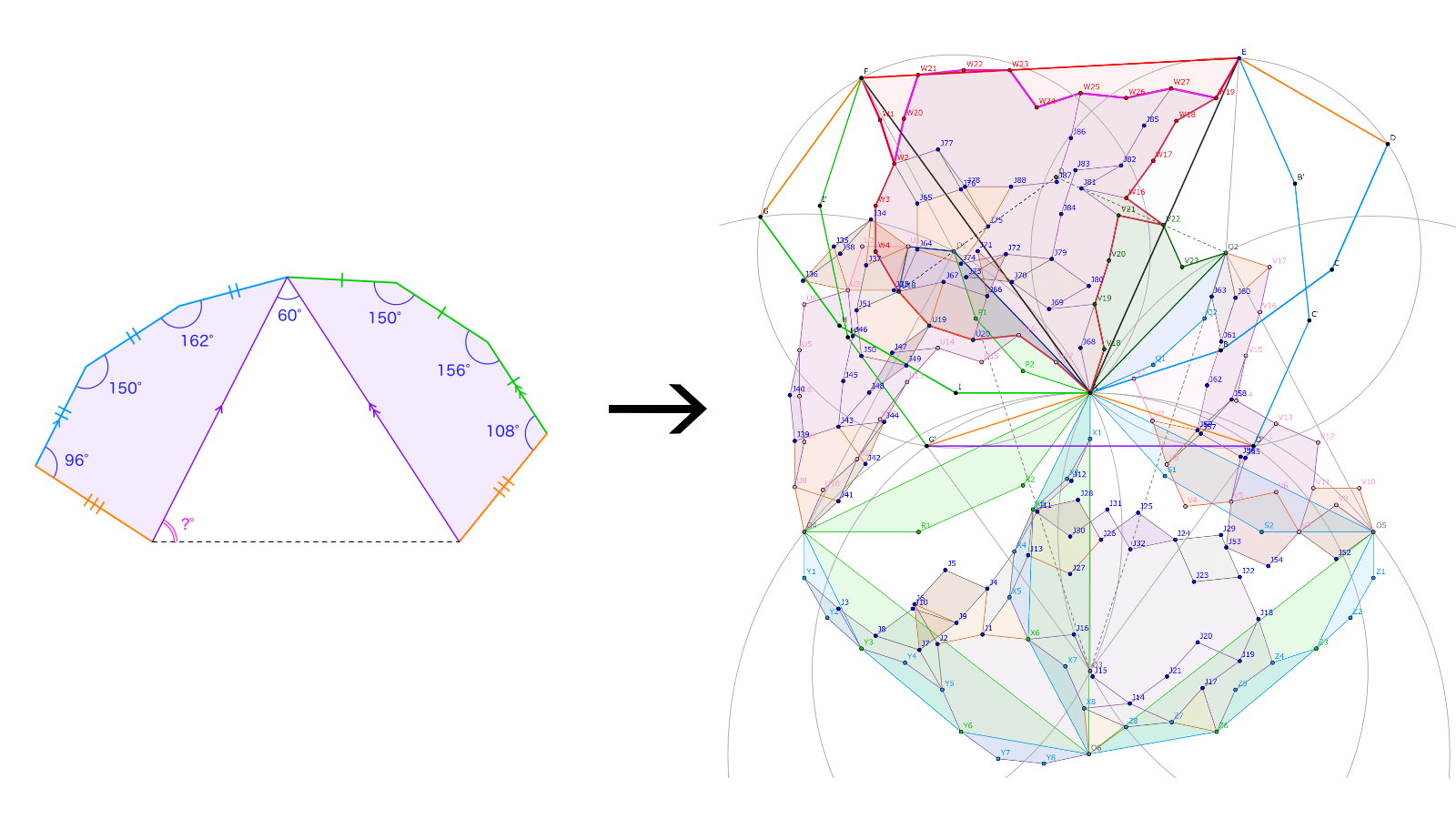
九角形$ABCDEFGHI$は$AB=BC=CD,$$DE=FG,$$GH=HI=IA$および$AE /\!/ CD,$$AF /\!/ HG$をみたします。$\angle ABC={162}^{\circ},$$\angle BCD={150}^{\circ},$$\angle CDE={96}^{\circ},$$\angle FGH={108}^{\circ},$$\angle GHI={156}^{\circ},$$\angle HIA={150}^{\circ},$$\angle EAF={60}^{\circ}$のとき、$\angle AEF$の大きさを求めてください。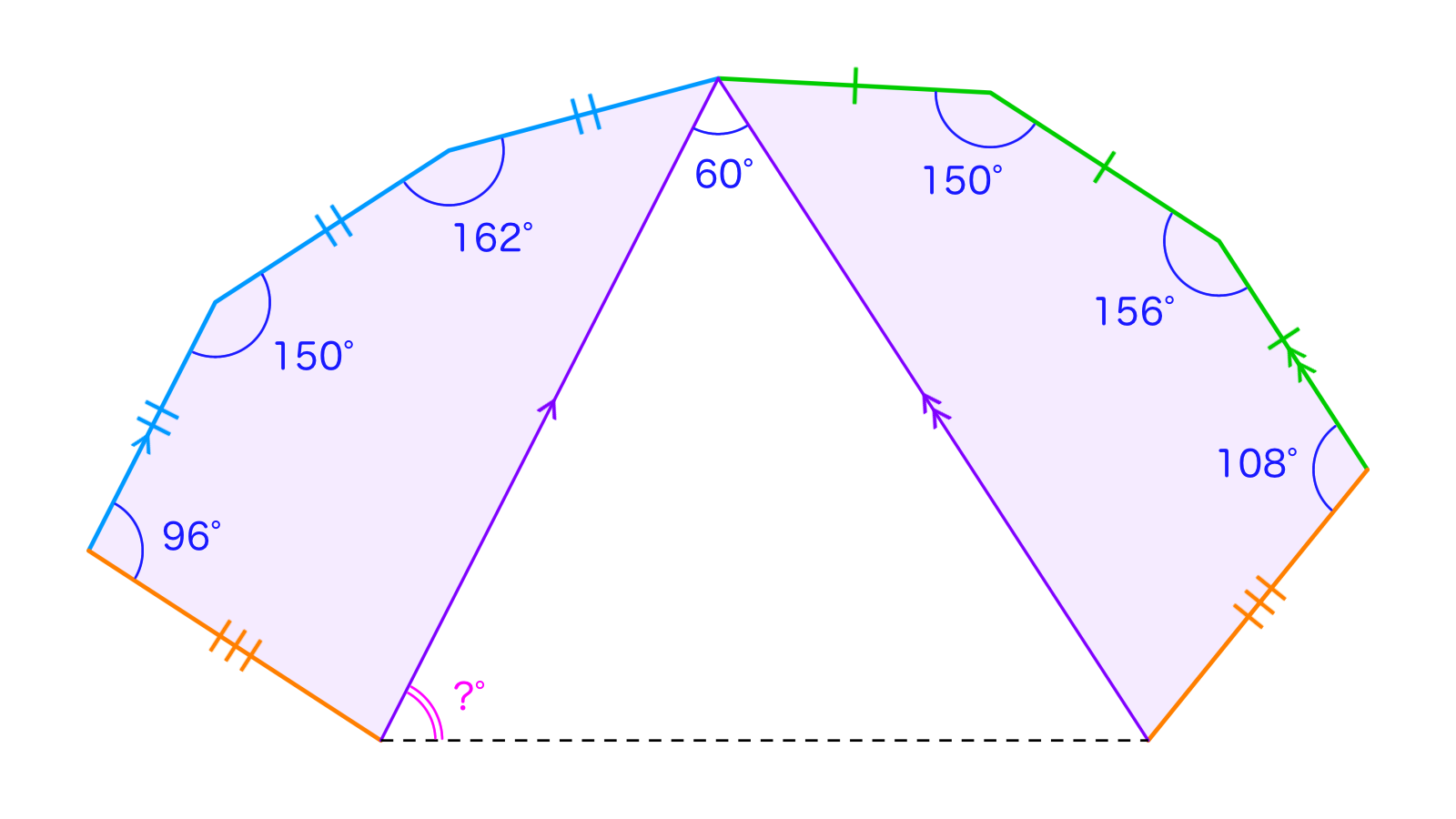
一瞬見ただけでは、これが問題3に由来することを見抜けないかと思われます。事実、問題3の結果を用いない別解も指摘されています(後述)。ですが、導入パートを読破してしまった以上、ひとまず問題3らしい解き方を試したくなるのが一般的感性というものでしょう。
ということで解きます。紙とペンとGeoGebraを十分に確保してください。
宣伝: T-GUESS Cupの解説記事一覧 (シリーズ化しました)
補助折れ線
五角形$ABCDE,$$AFGHI$をそれぞれ線分$AE,AF$の垂直二等分線について対称移動し、五角形$EB'C'D'A,$$AG'H'I'F$を作ります。すると$\triangle AD'G'$は$AD'=AG'$の二等辺三角形になり、$\angle AD'G'$$=\angle AG'D'$$={18}^{\circ}$となります。$\overrightarrow{G'D'}$の偏角を$0^{\circ}$と定めると、折れ線$FI'H'G',$$D'C'B'E$は整角三等辺経路になるので、四角形$FG'D'E$と点$A$について問題3が使えるのですね。分かりやすいように、ここからは$\overrightarrow{G'D'}$が右向きとなるように図を回転させます。
$\triangle AFG',$$\triangle AED',$$\triangle AG'D'$の外心を各々$O_1,O_2,O_3$とし、$\triangle AO_1O_3,$$\triangle AO_2O_3$の外心を各々$O_4,O_5$、$\triangle AO_4O_5$の外心を$O_6$とします。補題3の要領で、経路$GHIA$と相似な整角三等辺経路$O_1P_1P_2A,$$O_4R_1R_2A$を、経路$ABCD$と相似な整角三等辺経路$AQ_1Q_2O_2,$$AS_1S_2O_5$を、それぞれ図のように描いていくことが可能です。描き終えたところで、$\arg\overrightarrow{O_1R_1}={0}^{\circ},$$\arg\overrightarrow{R_1R_2}={24}^{\circ},$$\arg\overrightarrow{R_2A}={54}^{\circ},$$\arg\overrightarrow{AS_1}={-48}^{\circ},$$\arg\overrightarrow{S_1S_2}={-30}^{\circ},$$\arg\overrightarrow{S_2O_5}={0}^{\circ}$を算出しておきましょう。
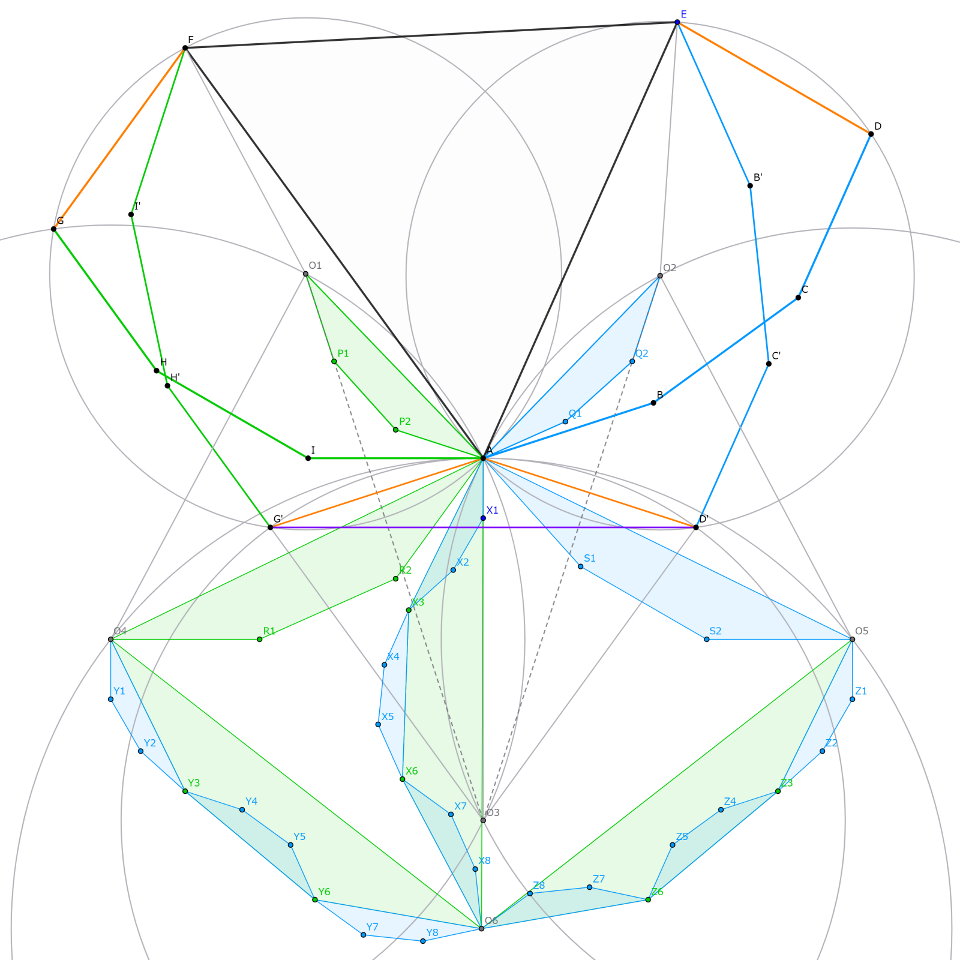
$\triangle AO_4O_5$に補題3を用います。経路$O_4R_1R_2A$と正の向きに相似な経路$AX_3X_6O_6,$$O_4Y_3Y_6O_6$および負の向きに相似な経路$O_5Z_3Z_6O_6$を描き、経路$AS_1S_2O_5$と正の向きに相似な経路$X_3X_22X_1A,$$X_3X_4X_5X_6,$$O_6X_8X_7X_6,$$O_5Z_1Z_2Z_3,$$Z_6Z_5Z_4Z_3,$$O_6Z_8Z_7Z_6$および負の向きに相似な経路$Y_3Y_2Y_1O_4,$$Y_3Y_4Y_5Y_6,$$O_6Y_8Y_7Y_6$を設けます。補題3より点$A,O_4,O_5$から点$O_6$に向かう各々の経路は整角九等辺経路となるので、$\overrightarrow{O_4A},\overrightarrow{AO_5}$も整角ベクトル18本の合成として表すことができるのですね。整角九等辺経路の各辺の偏角を具体的に計算し、
$$\begin{align*}
\arg\overrightarrow{AO_6}&=\arg\left(\sum_{k=-90,-120,-138,-114,-96,-66,-36,-66,-84}z^k\right) \\
\arg\overrightarrow{O_4O_6}&=\arg\left(\sum_{k=-90,-60,-42,-18,-36,-66,-36,-6,12}z^k\right) \\
\arg\overrightarrow{O_5O_6}&=\arg\left(\sum_{k=-90,-120,-138,-162,-144,-114,168,-174,-144}z^k\right) \\
\end{align*}$$と表せます(ただし$z=\exp\left(\dfrac{i\pi}{180}\right)$です)。
時短の方略
この要領で経路をペタペタ貼り付ければ先述の通り整角百二十六等辺経路を得ることになりますが、手計算で解く以上は少し楽をしたいです。よって、$\overrightarrow{O_4A},\overrightarrow{AO_5}$に相当する整角十八等辺経路を予め整理し、可能な限り短い経路に変えておきます。以降、角度計算の省略が著しいので、図をうまく用いつつどうにか解読してください。
点対称な十角形$Y_5Y_6Y_7$$Y_8O_6X_8$$X_7X_6J_1J_2$を描けば、$\triangle X_6X_5J_1$は正三角形となります。平行四辺形$Y_1Y_2Y_3J_3$、反時計回りの正五角形$J_2J_1J_4J_5J_6$、平行四辺形$Y_5J_2J_6J_7$を順に作図すると、$X_5X_4 /\!/ J_1J_4,$$Y_3J_3 /\!/ Y_5J_7$を確かめられるので、$J_4X_4=J_1X_5$、また点対称な六角形$J_3Y_3Y_4Y_5J_7J_8$を描くことが可能です。反時計回りの正三角形$J_6J_7J_9$、平行四辺形$J_8J_7J_9J_{10}$、点対称な六角形$X_1X_2X_3X_4J_{11}J_{12}$を描けば、ここまでの計算から経路$Y_1J_3J_8$$J_{10}J_9J_4$$X_4J_{11}J_{12}X_1$は整角九等辺経路となるので、$O_4Y_1 /\!/ AX_1$より点対称な二十角形$Y_1J_3J_8J_{10}$$J_9J_4X_4J_{11}$$J_{12}X_1AU_{17}$$U_{16}U_{15}U_{14}U_{13}$$U_{12}U_{11}U_{10}O_4$を描くことにより、点$O_4$と点$A$を結ぶ整角九等辺経路$O_4U_{10}U_{11}$$\dots U_{17}A$を完成させられました(この経路の各辺は元の整角十八等辺経路のそれと明らかに等長です)。
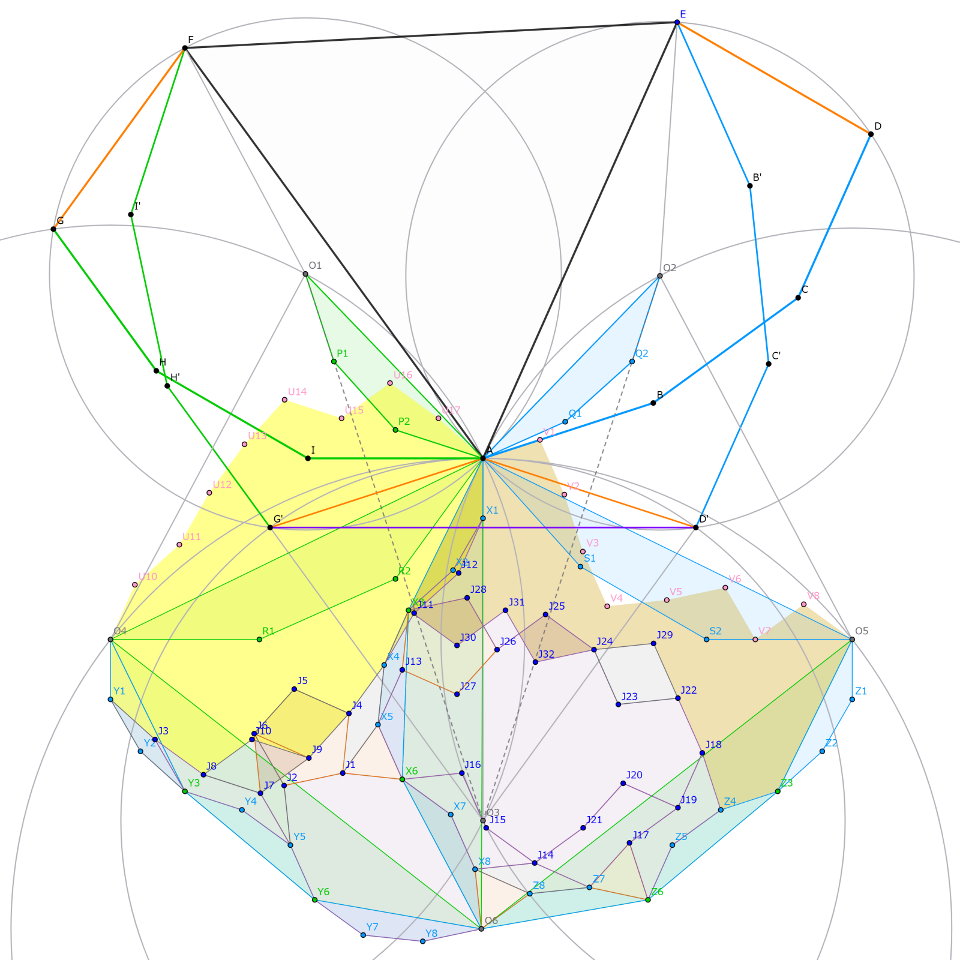
$\overrightarrow{AO_5}$側も大筋は一緒です。$\triangle X_8O_6Z_8$が正三角形であることを確かめたのち、平行四辺形$X_3X_4X_5J_{13},$$X_8Z_8Z_7J_{14}$、点対称な六角形$X_6X_7X_8$$J_{14}J_{15}J_{16}$、反時計回りの正三角形$Z_7Z_6J_{17}$を順に描きます。点対称な六角形$J_{17}Z_6Z_8$$Z_4J_{18}J_{19},$$J_{14}Z_7J_{17}$$J_{19}J_{20}J_{21}$を用意し、点対称な十六角形$J_{13}X_5X_6J_{16}$$J_{15}J_{14}J_{21}J_{20}$$J_{19}J_{18}J_{22}J_{23}$$J_{24}J_{25}J_{26}J_{27}$を描きましょう(途中で$J_{13}X_5 /\!/ J_{18}J_{19}$を用いました)。$\angle X_3J_{13}J_{27}$$=\angle J_{13}J_{27}J_{26}$$={108}^{\circ}$より、正五角形$X_3J_{13}J_{27}J_{26}J_{28}$を作れます。平行四辺形$J_{24}J_{23}J_{22}J_{29}$、点対称な八角形$J_{24}J_{25}J_{26}J_{28}$$X_3J_{30}J_{31}J_{32}$を描き、経路$AX_1X_2X_3,$$O_5Z_1Z_2Z_3$が平行移動のみで重なることに注意すると、点対称な二十角形$AX_3J_{30}J_{31}$$J_{32}J_{24}J_{29}J_{22}$$J_{18}Z_4Z_3O_5$$V_8V_7V_6V_5$$V_4V_3V_2V_1$が描けて、経路$AV_1V_2$$\dots V_8O_5$が点$A$と点$O_5$を結ぶ整角九等辺経路になるのです。元々十八等辺だったものが両方九等辺になったので、単純に考えて計算量が(ほぼ)半減しました。
点$O_4$について点$A$を反時計回りに${36}^{\circ}$回転させれば点$O_1$と重なるため、点$O_4$について経路$O_4U_{10}U_{11}$$\dots U_{17}A$を反時計回りに${36}^{\circ}$回転させた整角九等辺経路$O_4U_8U_7$$\dots U_1O_1$を作れます。同様に、点$O_5$について経路$AV_1V_2$$\dots V_8O_5$を時計回りに${36}^{\circ}$回転させた整角九等辺経路$O_2V_{17}V_{16}$$\dots V_{10}O_5$を作れます。$O_4=U_9,$$O_5=V_9$と別名を付ければ、整角十八等辺経路$O_1U_1U_2$$\dots U_{17}A,$$AV_1V_2$$\dots V_{17}O_2$の完成です。これらの経路も、先程と同じく簡略化してみましょう。
平行四辺形$U_1U_2U_3J_{33}$を描くと正五角形$U_3J_{33}U_1J_{34}J_{35}$が描けるので、反時計回りの正三角形$U_3J_{35}J_{36},$$U_1J_{34}J_{37}$、平行四辺形$J_{34}J_{35}J_{36}J_{38}$、点対称な六角形$U_5U_6U_7$$U_8J_{39}J_{40}$、平行四辺形$U_{11}U_{10}U_9J_{41}$を順に描いていきます。$\triangle U_8U_9J_{41}$は正三角形ですから、正五角形$J_{39}U_8J_{41}J_{42}J_{43}$、平行四辺形$U_{11}J_{41}J_{42}J_{44}$を描けて、さらに$\triangle J_{43}J_{42}J_{44}$も正三角形です。$U_3U_4 /\!/ J_{43}J_{39}$より、点対称な八角形$U_3U_4U_5J_{40}$$J_{39}J_{43}J_{45}J_{46}$が作れて、点対称な六角形$J_{43}J_{44}U_{13}$$U_{14}J_{47}J_{48},$$J_{47}U_{14}U_{15}$$U_{16}U_{20}U_{19}$、平行四辺形$U_{19}J_{47}J_{48}J_{49}$、反時計回りの正五角形$J_{49}U_{19}U_{18}J_{51}J_{50}$も順に作れますね。すると$U_1J_{37} /\!/ U_{18}J_{51}$から$U_1U_{18}$$=J_{37}J_{51}$が成立し、経路$O_1U_1U_{18}U_{19}$$U_{20}U_{16}U_{17}A$が整角七等辺経路となるとなるのです。今更ながら、詳細な偏角計算を省くことに罪悪感が湧いてきました。頑張ってついてきてください。
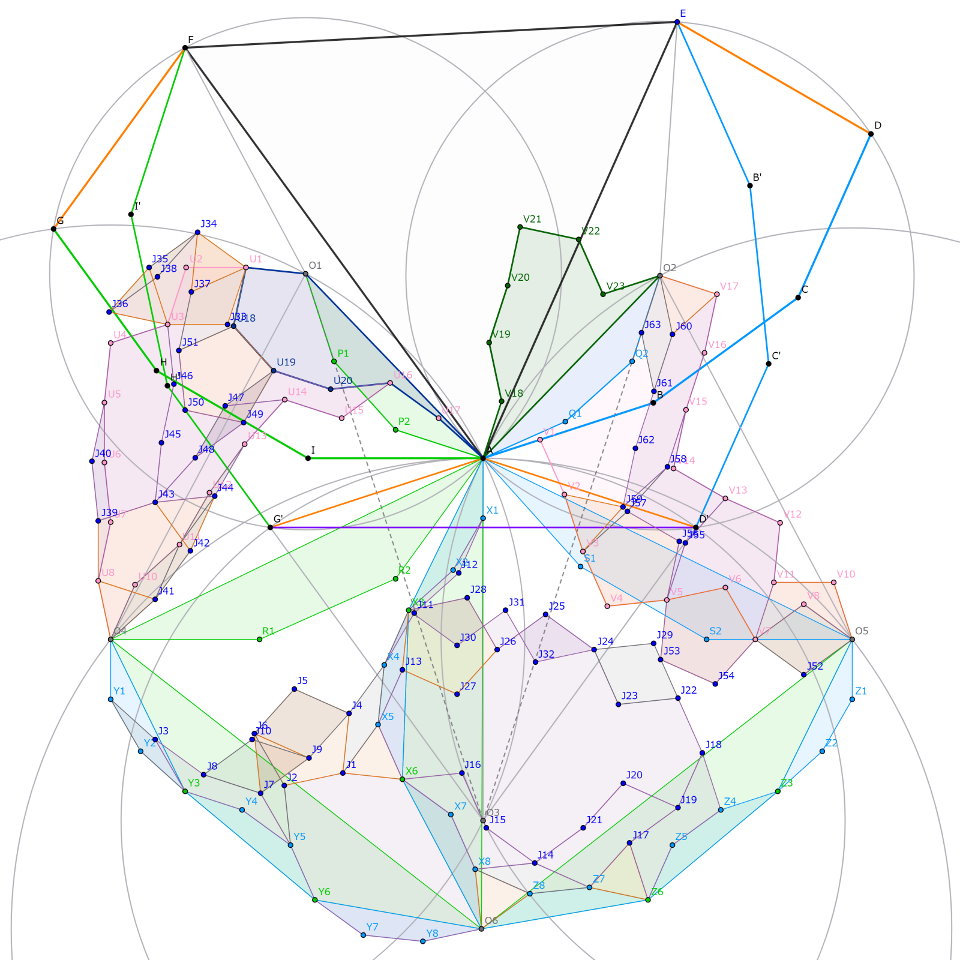
反対側です。平行四辺形$V_9V_8V_7J_{52}$を描くと正五角形$V_9V_{10}V_{11}V_7J_{52}$が現れ、正五角形$V_7V_6V_5J_{53}J_{54}$を描くと点対称な八角形$V_5J_{53}J_{54}V_7$$V_{11}V_{12}V_{13}J_{55}$を拵えられます。正五角形$V_3V_4V_5J_{56}J_{57}$を描くことで、点対称な八角形$J_{57}J_{56}V_5J_{55}$$V_{13}V_{14}V_{15}J_{58}$、平行四辺形$V_3J_{57}J_{58}J_{59}$、点対称な八角形$J_{59}J_{58}V_{15}V_{16}$$V_{17}J_{60}J_{61}J_{62}$を順に描いていけます。すると2つの正三角形$V_2V_3J_{59},$$V_{17}O_2J_{60}$ができますから、平行四辺形$J_{61}J_{60}O_2J_{63}$ののちに点対称な十四角形$AV_1V_2J_{59}$$J_{62}J_{61}J_{63}$$O_2V_{23}V_{22}$$V_{21}V_{20}V_{19}V_{18}$を用意できて、整角七等辺経路$AV_{18}V_{19}$$\dots V_{23}O_2$を作れるのです。これで$\overrightarrow{O_1A},\overrightarrow{AO_2}$の両方を整角ベクトル7本の合成に対応させられました。
次のサブセクションに行く前に、少しだけ考察を加えます。$\triangle AEF$の外心を$O$とすると、明らかに$AF \perp OO_1,$$AE \perp OO_2$です。簡単な偏角計算から$AF \perp U_{18}O_1,$$AE \perp V_{22}O_2$なので、3点の組$(O,O_1,U_{18}),$$(O,V_{22},O_2)$はいずれも同一直線上に存在しますね。このことを覚えておきましょう。
対称性の妙
経路$U_{18}U_{19}U_{20}$$U_{16}U_{17}A$を直線$OO_1$で対称移動させます。前述した考察より、こうして作られる経路の始点は$U_{18}$、終点は$F$となるので、作られた経路は$U_{18}W_4W_3$$W_2W_1F$と表せて、これもまた各辺の偏角が整数度です(直線$OO_1$の偏角が整数度であるため)。同様に経路$AV_{18}V_{19}$$V_{20}V_{21}V_{22}$を直線$OO_2$で対称移動移動させた経路$EW_{19}W_{18}$$W_{17}W_{16}V_{22}$も設けてあげます。$U_{18}=W_5,$$U_{19}=W_6,$$U_{20}=W_7,$$U_{16}=W_8,$$U_{17}=W_9,$$A=W_{10},$$V_{18}=W_{11},$$V_{19}=W_{12},$$V_{20}=W_{13},$$V_{21}=W_{14},$$V_{22}=W_{15}$と別名を付けると、整角二十等辺経路$FW_1W_2$$\dots W_{19}E$が完成し、問題4の解決まであと一息となります。今までの地道な計算のおかげで、百二十六等辺を二十等辺まで削減できたのです。やる気がみなぎりますね。
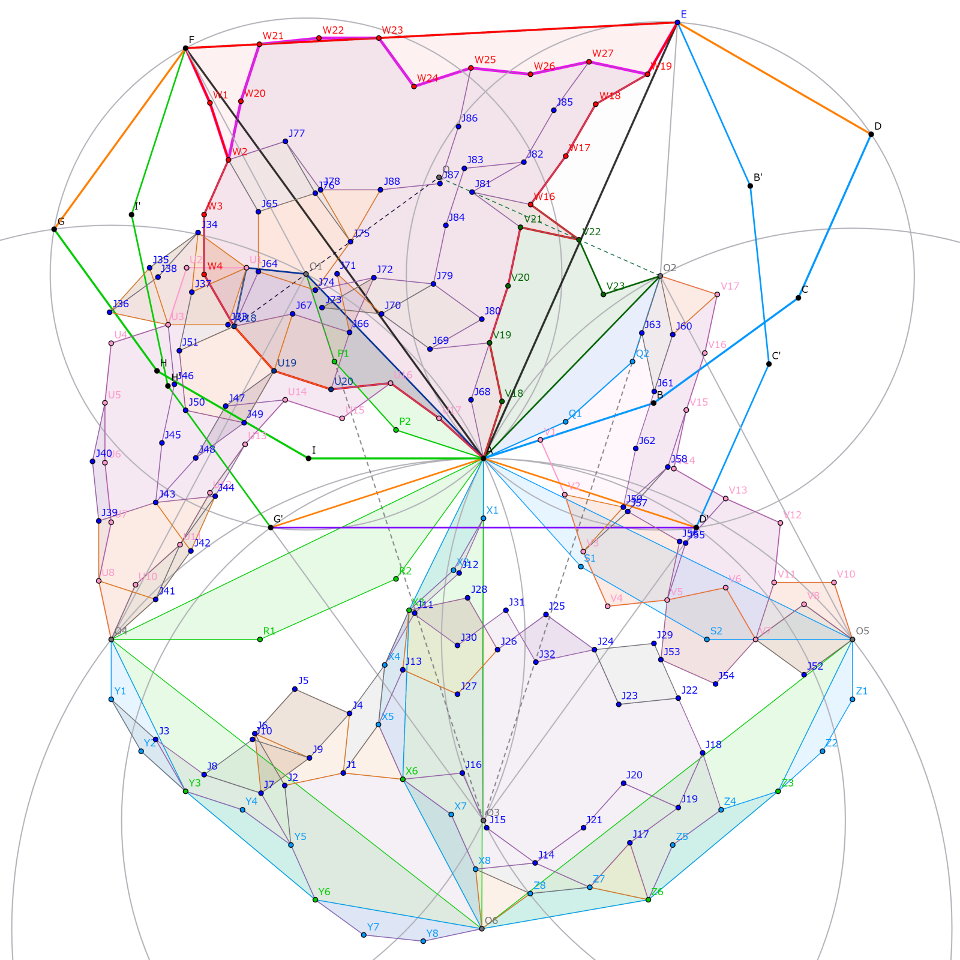
一気に駆け抜けます。点対称な六角形$W_2W_3W_4$$W_5J_{64}J_{65}$、正方形$W_6W_7J_{66}J_{67}$、平行四辺形$W_{10}W_{11}W_{12}J_{68}$、点対称な十角形$J_{66}W_7W_8W_9$$W_{10}J_{68}W_{12}$$J_{69}J_{70}J_{71}$を描けば、$\triangle W_5W_6J_{67}$は正三角形です。五芒星$J_{70}J_{71}J_{66}J_{72}J_{73}$、反時計回りの正五角形$J_{65}J_{64}J_{74}J_{75}J_{76}$、平行四辺形$W_2J_{65}J_{76}J_{77},$$J_{77}J_{76}J_{75}J_{78},$$J_{72}J_{73}J_{70}J_{79},$$J_{79}J_{70}J_{69}J_{80},$$W_{14}W_{15}W_{16}J_{81}$を順に描き加えれば、随所の平行に着目し点対称な十角形$J_{79}J_{80}J_{69}$$W_{12}W_{13}W_{14}$$J_{81}J_{82}J_{83}J_{84}$、点対称な八角形$J_{81}W_{16}W_{17}W_{18}$$W_{19}W_{27}J_{85}J_{82}$を拵えられます。$J_{75}J_{74} /\!/ W_{27}J_{85}$を用いて点対称な十四角形$J_{75}J_{74}J_{72}$$J_{79}J_{84}J_{83}J_{82}$$J_{85}W_{27}W_{26}$$W_{25}J_{86}J_{87}J_{88}$を用意すると、$\triangle J_{78}J_{75}J_{88}$が正三角形となるため、点対称な十二角形$W_2J_{77}J_{78}J_{88}$$J_{87}J_{86}W_{25}W_{24}$$W_{23}W_{22}W_{21}W_{20}$の作図とともに整角十二等辺経路$FW_1W_2W_{20}$$W_{21}W_{22}W_{23}$$W_{24}W_{25}W_{26}$$W_{27}W_{19}E$が顕現します(この経路を$\rho$とします)。
$\rho$の各辺の偏角を順に書き並べると以下の通りです。
$${-66}^{\circ},{-72}^{\circ},{78}^{\circ},{72}^{\circ},{6}^{\circ},{0}^{\circ},{-54}^{\circ},{18}^{\circ},{-6}^{\circ},{12}^{\circ},{-12}^{\circ},{60}^{\circ}$$ これらを$3^{\circ}$ずつ時計回りに回転させてみましょう。
$${-69}^{\circ},{-75}^{\circ},{75}^{\circ},{69}^{\circ},{3}^{\circ},{-3}^{\circ},{-57}^{\circ},{15}^{\circ},{-9}^{\circ},{9}^{\circ},{-15}^{\circ},{57}^{\circ}$$ 第1~4項、第5~6項、第7~12項に分けて考えると、対称性からこれらの偏角の合成は明らかに$0^{\circ}$です。ということは、回転前の偏角を合成すれば$3^{\circ}$となるため、$\arg\overrightarrow{FE}=3^{\circ}$なのです。やっと、やっと$\overrightarrow{FE}$の偏角に到達しました。最後の力を振り絞り計算すれば$\arg\overrightarrow{AE}={66}^{\circ}$となるため、$\angle AEF=$${63}^{\circ}$が本問の答えです。実演も一苦労ですね……。
解答の強調
問題F ${63}^{\circ}$
想定解における補助点は190個、補助線は304本でした(うち補助円は6個)。 こちら から、上記の解説図をGeoGebraで開くことができます。読み込みに10秒ほどかかるため、覚悟を決めてから開いてください。
余談パート
別解が優秀
問題4には別解が存在します。角度設定がたまたま都合のよいものであったため、はじめから整角二十四等辺経路を構成できてしまうのです。この事実は 立見鶏 氏に指摘されました。以下、氏による別解となります(筆者多忙につき答案画像をそのまま用いております、申し訳ございません)。
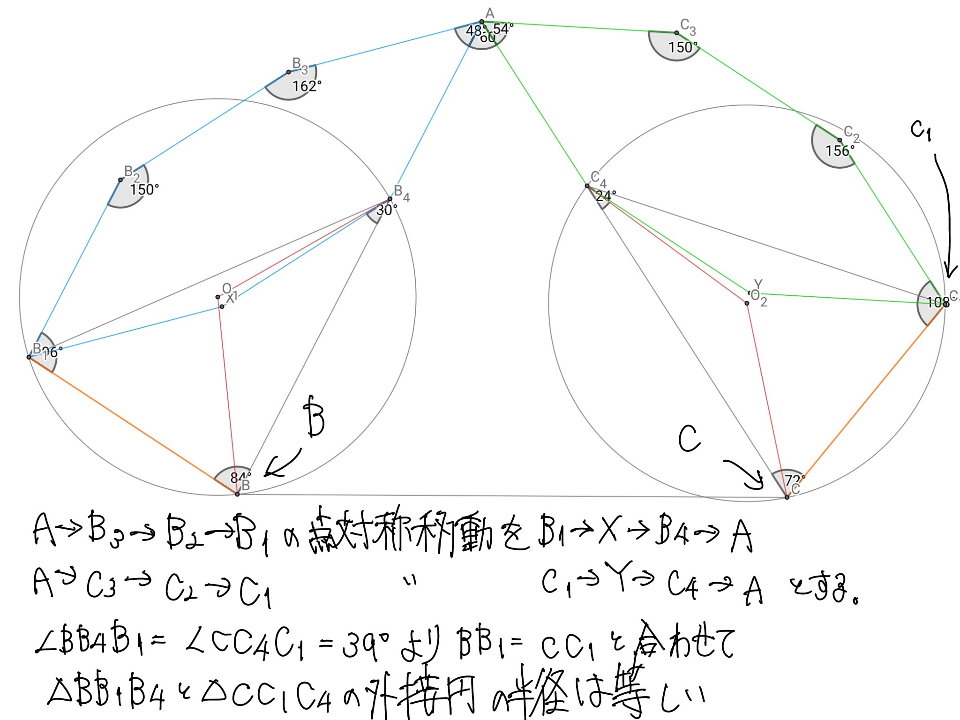
筆者が点の名前を指定せず出題したため、少々変更されております。角度計算と正弦定理により、円$BB_4B_1$と円$CC_1C_4$の半径が一致します。
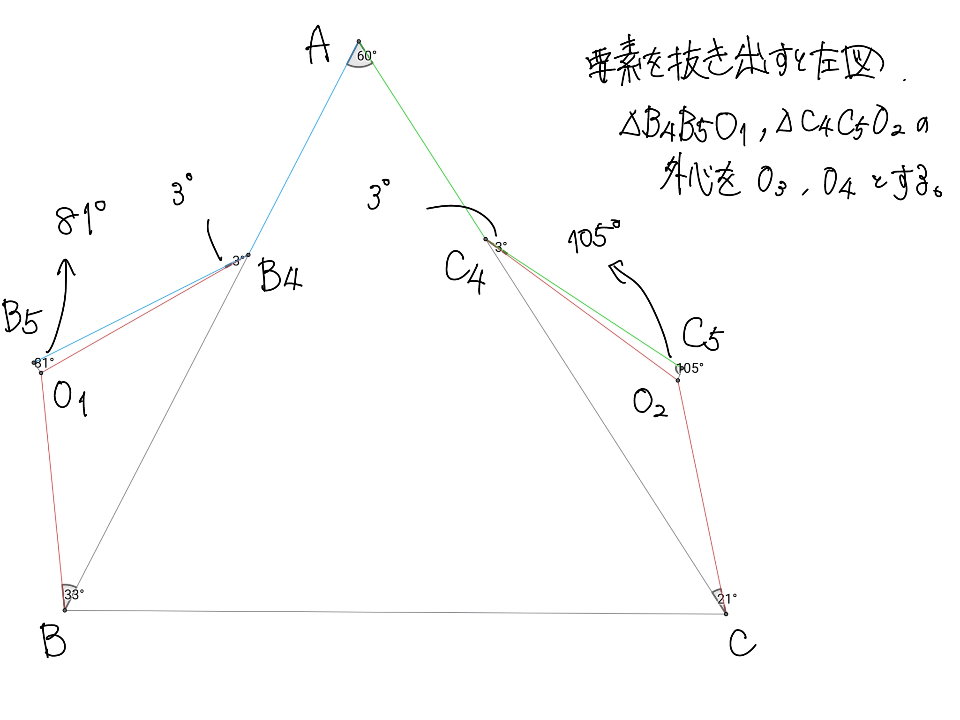
先程の図の点$X$を直線$B_4O_1$で対称移動し、点$B_5$を作ります。また$Y=C_5$と別名を付ければ、$O_1X \perp B_4B_1,$$O_2C_5 \perp C_1C_4$より、$\triangle B_4B_5O_1,$$\triangle C_4C_5O_2$の内角が判ります。
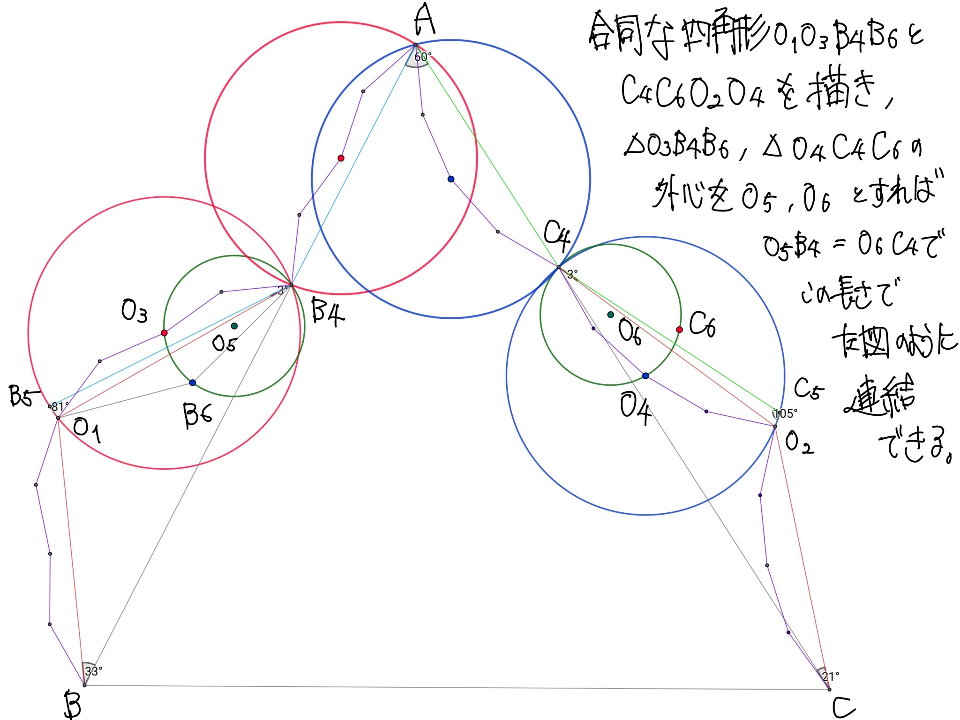
頂角${162}^{\circ}$の二等辺三角形$O_1O_3B_4$と頂角${150}^{\circ}$の二等辺三角形$C_4O_4O_2$をもとに、上図のような折れ線を作ることで、整角二十四等辺経路が完成します。

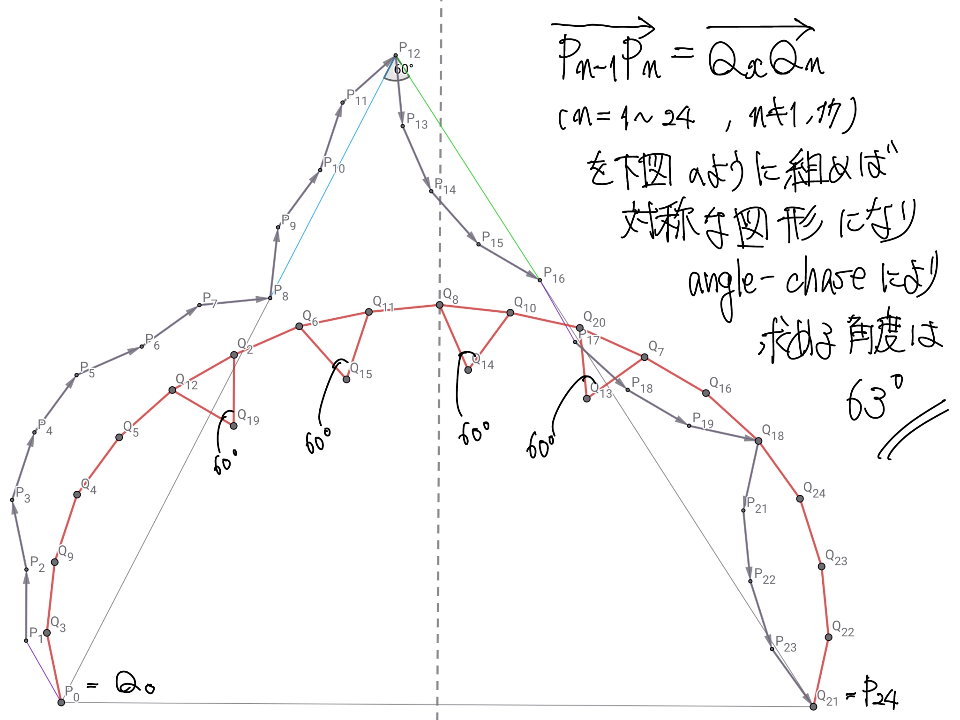
ここの行間が広いですが、実演パートで行ったように正多角形構成と平行移動をうまく活用すれば$\angle P_{12}P_0P_{24}=$${63}^{\circ}$が導出され、解答完了です。コンテストのラスボスとしての難しさは健在ですが、想定解よりは結構ナーフされました(ほか、三角関数の和積・積和変換で解き切った猛者もいらっしゃいます)。
主催者の声
第5回匿式図形問題エスパー杯の各問題の感想を、主催者の視点で述べていきます。まず、第3回・第4回では、邪悪な曲線ことレムニスケートに関連した出題もございましたが、今年は不作であり落ち着いた問題セットとなりました。深刻な問題飢饉のなかで得られた少数の幾何をさらに厳選し、下記6問をご覧いただいた次第です。
問題Aは、上質な作問で知られる
翔子さん
様に提供していただきました。後述の問題Dを事前に作っていたため、有難い反面「図の見た目が被ったな……」と感じたものですけれども、本問の集客効果は凄まじく、コンテスト参加者の多くはAから順に解答されていました。やはりbasic(幾何力の礎となる、的なニュアンスで)な問題は良いですね。
問題Bは筆者の自作です。「未知の長さを文字で置く」という基本操作が重要な問題であり、どちらかといえば代数らしい雰囲気が出ていたかもしれません。ちなみに、正方形を面積$36$の任意の長方形に変えても答えは不変です。お気づきでしたか?
続く問題Cは、様々な数学コンの受賞歴をもつ
nmoon
様からのご提供です。相変わらず人々は綺麗な問題を作ってきますね(本音)。本質的には余弦定理一発なのですが、意外と見えづらい円周角で参加者の得点を阻みました。この問題における$\angle EAF$$+\angle BPD$$={180}^{\circ}$を構図として覚えておけば、いずれ良いことがあるはずです。
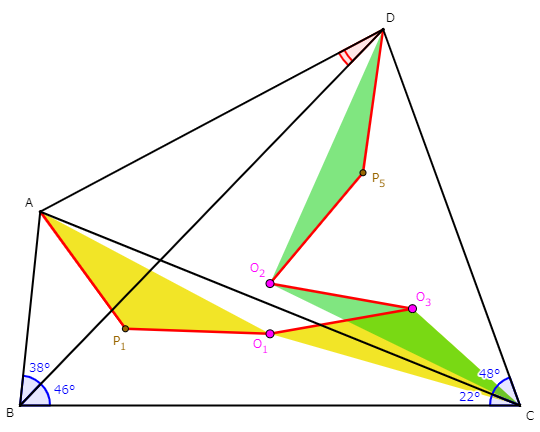
そして問題D。中受典型として知られる
ヒポクラテスの三日月
の、筆者による拡張です。流行れ(本音再び)。D以降の問題は、初見での「これ求められるの?」感を基準に仕上げました。求められます。これを。実は。
問題E。筆者オリジナルの中で特にオススメの一作です。辺の三等分という、求角問題との相性が一見最悪の設定に、初等幾何学最高の美しさとも讃えられる
フランク・モーリーの定理
を込めました。こちらも一部参加者から別解をいただいております。
トリを飾った問題Fにつきましては、考察含め作問に2か月近く(正味で約120時間)かかった難産っ子です。元々は後述する問題5のようなモンスターを出題予定であったものの、非本質部分が多すぎるということで現行の九角形へと差し替えました。なお、上記解説図を描くだけでも10時間以上かかったという裏話があり、「そんなものをコンテストに出すな」と各所より非難が湧き上がるのを肌に感じております。
6問を通じ、作問難易度>>>>>解答難易度であったと自負します。例えば問題Bは、参加者平均得点率が70%を超える易問ですが、一方で本問をゼロから思いつける参加者が70%もいらっしゃるかと問われれば首を縦に振れません(多めに見積もっても40%くらいかと考えます)。事実、主催者にとっては初等幾何研究歴7年弱にして漸く到達した性質です。9日間のコンテストにはあまりにも過剰な労力です。当然ながら、他の設問の作問コスパも同様に散々なものでございまして、コスパの上げ方を誰かご存じでしょうか……と途方に暮れる主催者がいます。哀れですね。
有用性とは
このセクションまで辿り着けた皆様であれば、外心の威力がどれほどのものであるか、よく理解されていると思われます。偏角が整数度の場合に限って記しましたが、これを偏角が有理数度の場合にも拡張できることは言うまでもないでしょう。今や皆様は、有限個の整角$n$等辺経路により描かれうる任意の図形について、各部分の偏角を(有理数度であれば)初等的に求められるのです。例えば、こういった問題を解けます。
四角形$ABCD$の辺$AB,BC,$$CD,DA$上にそれぞれ点$E,F,G,H$をとり、四角形$EFGH$の内部に点$P$をとる。$\angle CFG,$$\angle GFP,$$\angle PFE,$$\angle APB,$$\angle BPF,$$\angle FPC,$$\angle CPD,$$\angle BAP,$$\angle PDC$の大きさがすべて整数度で与えられ、$EH /\!/ FG$が成立したとき、$\angle EHG$の大きさを補題3の手法で求めるためには整角$u$等辺経路を考える必要がある。$u\le 107520$を示しなさい。(以下に問題の一例を示します。)
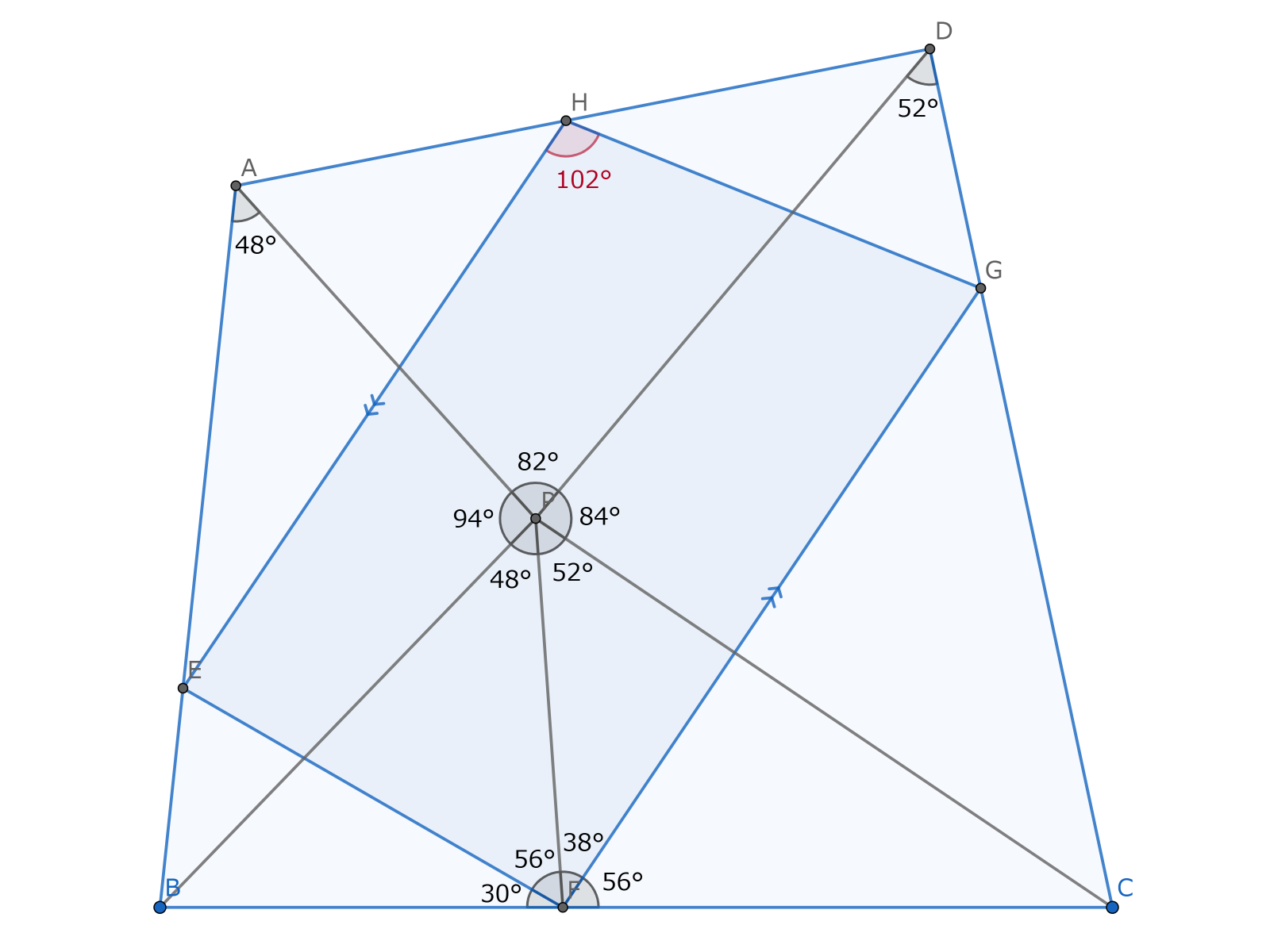
整角十万七千五百二十等辺経路。頑張れば手計算できますね。さあ、精々頑張りましょう……とは流石に言えなかったので、問題5の代わりに問題4を採用しました。ほか、ここまで複雑化すると三角関数解法のほうが遥かに美しくなってしまうため、という理由もあります。そして何より、万が一にも想定解通りに十万七千五百二十等辺十万七千五百二十一角形を描いてきた聡明な参加者がいらっしゃった場合を考えてみてください。採点者たる私に待ち受けている未来とは何か。死です。偏角をただ書き並べるだけでも推定500キロバイトに及び、しかもそれが経路変換のたびに何度もリライトされるのです。107520項の数列の転倒数は平均$\dfrac{107520\times 107519}{4}$$\approx 2.9\times {10}^9$ですから、仮に平行四辺形の構成のみで答案が書かれたならば、(行間の記述抜きで)推定1.4テラバイトの答案を採点することになります。比較として、地デジで1週間連続録画したときの容量が大体1.4テラバイトだそうです。どうして存命中に採点を終えられましょうか、いや終えられません。無理です。かくして問題5のお蔵入りに至り、contestantsとwin-winなrelationをbuildいたしました。
メッセージ
・整角$n$等辺経路で構成される求角問題には軒並み外心が使える
・補題3を用いれば、外心と各点の間に整角$n$等辺経路を設けられる
・採点時のこともよく考えて出題しようね
以上です。今回も約34,000字ほど書かせていただき、また問題4では120,000字以上のTikZコードに相当する解説図をお見せしました(GeoGebra全機能版でエクスポートした際の文字数)。読者に対する配慮がないのかと問われれば、なくはないです。ただ題材が重すぎるだけです。削れるだけ削った結果の34,000字といえます。例を挙げますと、もしも問題4の経路構成・変換に何の創意工夫も凝らさなければ、整角百二十六等辺経路の平均バブルソート回数をもとに概算し、補助点を3,800点ほど要していたはずなので。工夫で3,800点を190点に減らしました。これが筆者なりの配慮です。
ご感想・ご指摘・巧妙な解法・作業速度の上げ方などがございましたら、是非ともコメントに残していってください。ここまでお読みいただき、ありがとうございました。
