数学会報誌9月号
更新遅れて本当にごめんなさい!これからは会報誌はmathlogで書きますね。
夏休み中に書いた記事
ここに書いてある内容はすべて自信作なので
ぜひ読んでください。
OMC攻略① 動的計画法
OMCで無双しやすくなります。
OMC攻略② 偏微分
OMCで無双しやすくなります。
2回合成関数が一次関数となる離散単調増加関数について
夏休み中に私がマスフェスタで発表した内容です。
三角関数の上級者向け公式集
定期テスト、入試で役立つ公式集です。
※加法定理から和積まで全て頭に入っていることが前提です
数学オリンピック予選突破者の見直しの方法
数オリ民で計算ミスに悩まされている人は一度読んで下さい。
挑戦的問題集
任意の自然数nについて、ちょうどn個の格子点を通る円がかけることを証明せよ。
(1)3つの互いに接する円が与えられたとき、これら3つの円に接する円を2つ作図せよ。
(手法と、それでいつでも可能な証明を求める)
(2)ΔABCの内接三角形をΔDEFとして、内心をIとする。Aを中心としE,Fを通る円をωAとし、同様にωB,ωCを定める。ωAωBωCに接する円は2つあり、それぞれの中心をS,Tとする。また、AD,BEの交点をGとする。I,G,S,Tが共線であることを示せ。
雑多問題集
- Hを△ABCの垂心とし△ABC の垂心三角形をDEFとする
- △DEFの外接円とAB,ACの交点のうちF,DでないものをI,Jとする
- AEと△DEFの外接円の交点でEでないものをGとする
- AJ AD=112
- AB=24
- ΑΕ=16
以下の問に答えてください。 ただし条件4~6ではABで線分ABの長さを示すものとします。
- GHの長さを求めてください。
- GIの長さを求めてください。
自然数から自然数への単調増加関数が
次の条件を満たす。
・f(f(x))=2x+4
f(2025)を全て求めよ。
★2x+1のときがオリジナルの問題である。
2x+2,2x+3とか他の1次関数のときも考えてみよう。
前回の挑戦的問題集の解説
問題7
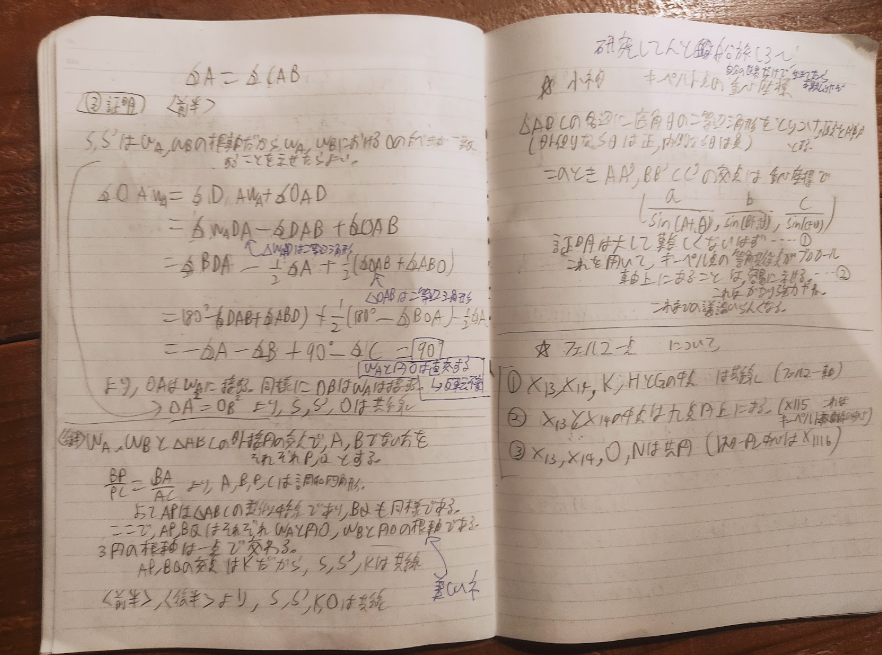 1
1
 2
2
問題8
 1
1
 2
2
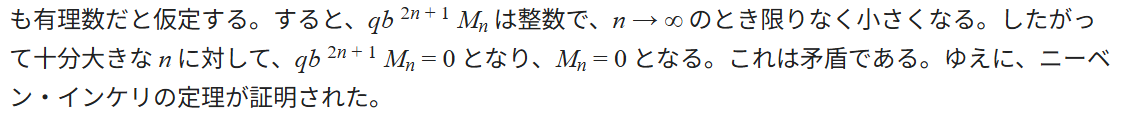 3
3
Vが有理数ならばV^2が有理数である
の対偶として、V^2が無理数ならばVが無理数であることは念頭に置いておく。
ニーベン・インケリの定理より、cos2は無理数だから、
cos^2(1)=(1+cos2)/2も無理数
よってtan^2(1)=1/(cos^2(1))-1も無理数だから、tan1は無理数である。
前回の雑多問題集の解答
問題7 6066
問題8
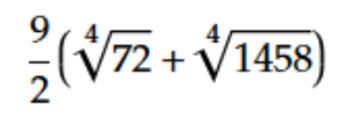 問題8の答え
問題8の答え
