楕円積分の3乗の積分について
楕円積分の$3$乗の積分について
楕円積分の$3$乗を含む級数について考えていきます。
楕円積分などを定義します。
\begin{align} K (x)&=\frac{\pi}{2}{}_2F_1\left[\begin{array}{}\frac12,\frac12\\1\end{array};x^2\right] \\\kappa(x)&={}_2F_1\left[\begin{array}{}\frac12,\frac12\\1\end{array};x\right] \\E (x)&=\frac{\pi}{2}{}_2F_1\left[\begin{array}{}-\frac12,\frac12\\1\end{array};x^2\right] \\K'(x)&=K\Big(\sqrt{1-x^2}\Big) \\E'(x)&=E\Big(\sqrt{1-x^2}\Big) \\\beta_n&=\frac{\binom{2n}{n}}{2^{2n}} \\\sum_{n=0}^{\infty}P_n(x)t^n&=\frac1{\sqrt{t^2-2tx+1}} \end{align}
あまり$E(x)$を見ることはありませんが、$E(x)$でもちゃんと計算できることを見せたいです。
準備のためにいくつか定理を用意します。
性質がいい$f(t)$に対して以下が成り立つ。
$$\int_{0}^{1}\frac{\mathrm{Im}f(\frac1x)}{x(1-tx)}dx=\pi f(t)$$
証明
まず、以下を示す。
$\displaystyle f\left(\frac1z+i0\right)-f\left(\frac1z-i0\right)$が$\mathrm{Re}(z)>0$で正則なとき、以下の等式が成り立つ。
$$\int_{0}^{1}\frac{f\left(\frac1x+i0\right)-f\left(\frac1x-i0\right)}{x(1-tx)}dx=2\pi if(t)$$
以下の積分経路で$\di\frac{f(z)}{z-t}$を積分する。
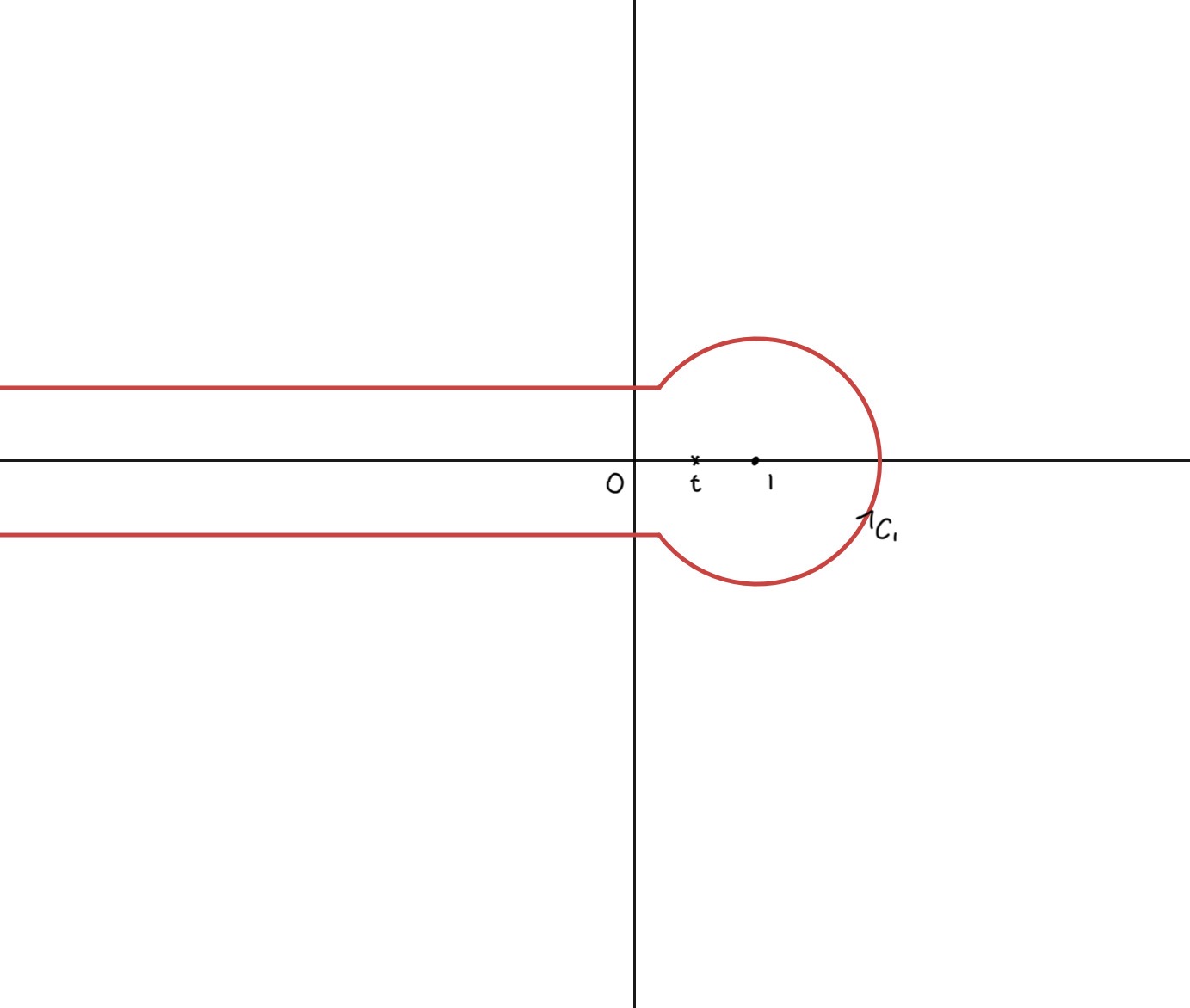 積分経路
積分経路
コーシーの積分定理より、
$$\oint_{C_1}\frac{f(z)}{z-t}dz=2\pi if(t)$$
円の部分は$0$になるので、
\begin{align*} \oint_{C_1}\frac{f(z)}{z-t}dz&=\int_{-\infty}^{1}\frac{-f(x+i0)+f(x-i0)}{x-t}dx \\&=\left(\int_{-\infty}^{0}+\int_{0}^{1}\right)\frac{-f(x+i0)+f(x-i0)}{x-t}dx \\&=\left(\int_{0}^{ー\infty}+\int_{\infty}^{1}\right)\frac{f(\frac1x+i0)-f(\frac1x-i0)}{x(1-tx)}dx \end{align*}
$\di g(x)=\frac{f(\frac1x+i0)-f(\frac1x-i0)}{x(1-tx)}$として、以下の積分経路で$g(x)$を積分する。
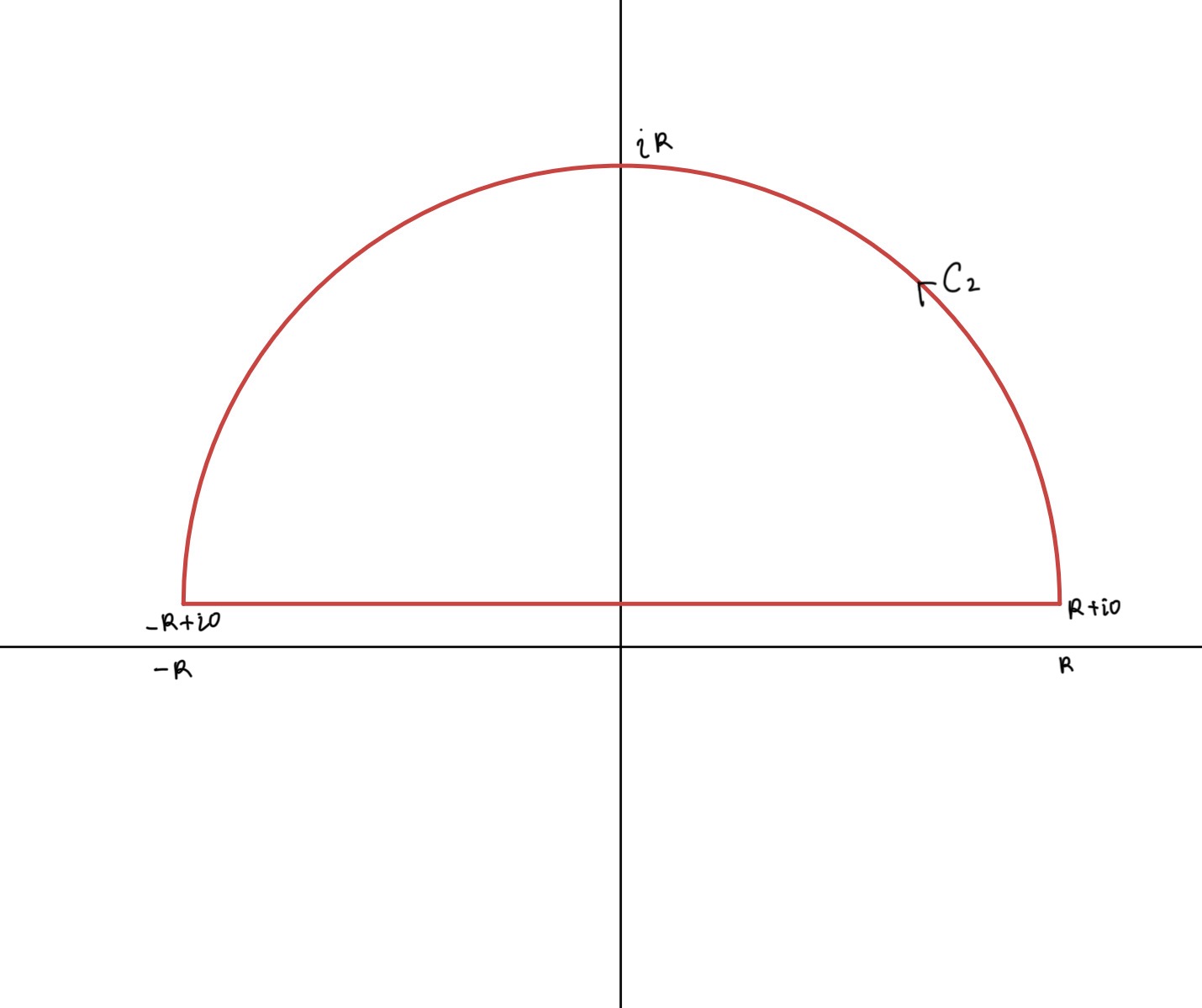 積分経路
積分経路
$f$の条件から全体の積分はコーシーの積分定理から$0$
円弧の部分は$R\to\infty$で$0$なので、$R\to\infty$としたとき、
$$\oint_{C_2}g(z)dz=\left(\int_{\infty}^{0}+\int_{0}^{1}+\int_{1}^{\infty}\right)g(x)dx$$
左辺は$0$になるので、区間を反転させると
\begin{align} \int_{0}^{1}g(x)dx&=\left(\int_{0}^{-\infty}+\int_{\infty}^{1}\right)g(x) \\&=\oint_{C_1}\frac{f(z)}{z-t}dz \\&=2\pi if(t) \end{align}
次に、以下を示す。
$f(x)$がべき級数展開可能なとき、以下の等式が成り立つ。
$$f(x+i0)-f(x-i0)=2i\mathrm{Im}f(x+i0)$$
$f(x)$がべき級数展開可能以外にも条件がありそうなのですが、あったりするのですかね、解析強い人教えて欲しいです。
$f(x)$はべき級数展開可能なので、数列$a_n$を用いて
$$f(x)=\sum_{n=0}^{\infty}a_nx^n$$
と表せる。
二項定理を用いて示す。後で$\varepsilon\to0$とします。
\begin{align*} f(x+i\varepsilon)&=\sum_{n=0}^{\infty}a_n(x+i\varepsilon)^n \\&=\sum_{n=0}^{\infty}a_{2n}(x+i\varepsilon)^{2n}+\sum_{n=0}^{\infty}a_{2n+1}(x+i\varepsilon)^{2n+1} \\&=\sum_{n=0}^{\infty}a_{2n}(x+i\varepsilon)^{2n}+\sum_{n=0}a_{2n+1}(x+i\varepsilon)^{2n+1} \\&=\sum_{n=0}^{\infty}a_{2n}\sum_{m=1}^{2n}\binom{2n}{m}x^{2n-m}(i\varepsilon)^m+\sum_{n=0}^{\infty}a_{2n+1}\sum_{m=0}^{2n+1}\binom{2n+1}{m}x^{2n-m+1}(i\varepsilon)^m \\&=\sum_{n=0}^{\infty}a_{2n}\left(\sum_{m=0}^{n}\binom{2n}{2m}x^{2n-2m}(i\varepsilon)^{2m}+\sum_{m=0}^{n-1}\binom{2n}{2m+1}x^{2n-2m-1}(i\varepsilon)^{2m+1}\right)+ \\&\ \ \ \sum_{n=0}^{\infty}a_{2n+1}\left(\sum_{m=0}^{n}\binom{2n+1}{2m}x^{2n-2m+1}(i\varepsilon)^{2m}+\sum_{m=0}^{n}\binom{2n+1}{2m+1}x^{2n-2m}(i\varepsilon)^{2m+1}\right) \\&=\sum_{n=0}^{\infty}a_{2n}\left(\sum_{m=0}^{n}\binom{2n}{2m}x^{2n-2m}(-1)^m\varepsilon^{2m}+i\sum_{m=0}^{n-1}\binom{2n}{2m+1}x^{2n-2m-1}(-1)^m\varepsilon^{2m+1}\right)+ \\&\ \ \ \sum_{n=0}^{\infty}a_{2n+1}\left(\sum_{m=0}^{n}\binom{2n+1}{2m}x^{2n-2m+1}(-1)^m\varepsilon^{2m}+i\sum_{m=0}^{n}\binom{2n+1}{2m+1}x^{2n-2m}(-1)^m\varepsilon^{2m+1}\right) \\&=\sum_{n=0}^{\infty}a_{2n}\sum_{m=0}^{n}\binom{2n}{2m}x^{2n-2m}(-1)^m\varepsilon^{2m}+\sum_{n=0}^{\infty}a_{2n+1}\sum_{m=0}^{n}\binom{2n+1}{2m}x^{2n-2m+1}(-1)^m\varepsilon^{2m}+ \\&\ \ \ i\Big(\sum_{n=0}^{\infty}a_{2n}\sum_{m=0}^{n-1}\binom{2n}{2m+1}x^{2n-2m-1}(-1)^m\varepsilon^{2m+1}+ \\&\ \ \ \sum_{n=0}^{\infty}a_{2n+1}\sum_{m=0}^{n}\binom{2n+1}{2m+1}x^{2n-2m}(-1)^m\varepsilon^{2m+1}\Big) \\&=A+Bi \end{align*}
$f(x-i\varepsilon)$についても同じ計算をすると、
$$f(x-i\varepsilon)=A-Bi$$
となるので、
\begin{align*} f(x+i\varepsilon)-f(x-i\varepsilon)&=A+Bi-A+Bi \\&=2iB \\&=2i\mathrm{Im}f(x+i\varepsilon) \end{align*}
$\varepsilon\to0$として、題意を得る。
先ほどの結果と合わせることで目標の定理を得る。
$$\kappa\left(\frac{1}{x}\right)=\sqrt{x}\Big(\kappa(x)+i\kappa(1-x)\Big)$$
証明
\begin{align*} \kappa\left(\frac1t+i\varepsilon\right)&=\frac{1}{\pi}\int_{0}^{1}\frac{dx}{\sqrt{x(1-x)\big(1-(\frac1t+i\varepsilon)x\big)}} \\&=\frac{1}{\pi}\left(\int_{0}^{t}\frac{dx}{\sqrt{x(1-x)\big(1-(\frac1t+i\varepsilon)x\big)}}+\int_{t}^{1}\frac{dx}{\sqrt{x(1-x)\big(1-(\frac1t+i\varepsilon)x\big)}}\right) \\&=\frac{1}{\pi}\left(t\int_{0}^{1}\frac{dx}{\sqrt{tx(1-tx)\big(1-(\frac1t+i\varepsilon)tx\big)}}+\int_{0}^{1-t}\frac{dx}{\sqrt{x(1-x)\big(1-(\frac1t+i\varepsilon)(1-x)\big)}}\right) \\&=\frac{1}{\pi}\left(\sqrt{t}\int_{0}^{1}\frac{dx}{\sqrt{x(1-tx)\big(1-(1+it\varepsilon)x\big)}}+\int_{0}^{1-t}\frac{dx}{\sqrt{x(1-x)\big(1-\frac1t-i\varepsilon+(\frac1t+i\varepsilon)x\big)}}\right) \end{align*}$\varepsilon\to0$として、
\begin{align*} \kappa\left(\frac1t\right)&=\frac1{\pi}\left(\sqrt{t}\int_{0}^{1}\frac{dx}{\sqrt{x(1-x)(1-tx)}}+\int_{0}^{1-t}\frac{dx}{\sqrt{x(1-x)\big(1-\frac1t+\frac1tx\big)}}\right) \\&=\sqrt{t}\kappa(t)+\frac1{\pi}(1-t)\int_{0}^{1}\frac{dx}{\sqrt{(1-t)x(1-(1-t)x)\big(1-\frac1t+\frac{1-t}{t}x\big)}} \\&=\sqrt{t}\kappa(t)+\frac1{\pi}i\sqrt{t}\int_{0}^{1}\frac{dx}{\sqrt{x(1-x)\big(1-(1-t)x\big)}} \\&=\sqrt{t}\big(\kappa(t)+i\kappa(1-t)\big) \end{align*}
よって、題意を得る。
\begin{align} K(x)&=\frac1{1+x}K\left(\frac{2\sqrt{x}}{1+x}\right) \\K'(x)&=\frac2{1+x}K\left(\frac{1-x}{1+x}\right) \end{align}
$$K\big(\sqrt{x}\big)K\big(\sqrt{1-x}\big)=\frac{\pi^3}{8}\sum_{n=0}^{\infty}\beta_n^4(4n+1)P_{2n}(2x-1)$$
$$K(\sqrt{x})=2\sum_{n=0}^{\infty}\frac{P_n(2x-1)}{2n+1}$$
$$\sum_{n=0}^{\infty}\frac{\beta_n^4}{4n+1}=\frac{\pi^3}{6\Gamma\left(\frac 34\right)^8}$$
$$K'(x)E(x)+K(x)E'(x)-K(x)K'(x)=\frac{\pi}{2}$$
準備ができたので求めていましょう。
楕円積分の累乗の指数の合計が$3$の積分を考えます。
$A,B$を定めます。
\begin{align} A&=\int_0^1K'(x)^3dx \\B&=\int_0^1E'(x)^3dx \end{align}
ちなみに、$A$の値はガンマ関数を用いて表せます。$B$は知りません。
以下、積分の一覧です。
\begin{align*} \int_0^1 K'(x)^3 \, dx &=A \\ \int_0^1 K(x)^3 \, dx &=\frac3{10}A \\ \int_0^1 K(x)^2 K'(x) \, dx &=\frac13A \\ \int_0^1 K(x) K'(x)^2 \, dx &=\frac12A \\ \int_0^1 K(x)^2 E(x) \, dx &=\frac15A \\ \int_0^1 K'(x)^2 E'(x) \, dx &=\frac13A \\ \int_0^1 K(x)^2 E'(x) \, dx &=\frac19A+\frac{2\pi}{3}\beta(2) \\ \int_0^1 K'(x)^2 E(x) \, dx &=\frac13A+\frac{\pi^3}{12} \\ \int_0^1 K(x) E(x)^2 \, dx &=-\frac{37}{240}A+\frac2{15}B-\frac15 \\ \int_0^1 K'(x) E'(x)^2 \, dx &=\frac4{27}A+\frac4{27}B+\frac{\pi}{3}\beta(2)+\frac{\pi}{6} \\ \int_0^1 K'(x) E(x)^2 \, dx &=\frac{13}{144}A-\frac{2}{9}B+\frac{\pi^3}{24} \\ \int_0^1 K(x) E'(x)^2 \, dx &=\frac4{27}A+\frac4{27}B+\frac{\pi}3\beta(2)+\frac{\pi}6 \\ \int_0^1 K(x) K'(x) E(x) \, dx &=\frac29A+\frac{\pi}{3}\beta(2)\\ \int_0^1 K(x) K'(x) E'(x) \, dx &=\frac16A+\frac{\pi^3}{24} \\ \int_0^1 K(x) E(x) E'(x) \, dx &=\frac2{27}A-\frac{4}{27}B+\frac{\pi}{2}\beta(2)+\frac{\pi}{12} \\ \int_0^1 K'(x) E(x) E'(x) \, dx &=\frac{11}{144}A+\frac{2}{9}B+\frac{\pi^3}{16} \\ \int_0^1 E(x)^3 \, dx &=\frac{37}{320}A-\frac{1}{10}B+\frac25 \\ \int_0^1 E'(x)^3 \, dx &=B \\ \int_0^1 E(x)^2 E'(x) \, dx &=\frac1{27}A+\frac{1}{27}B+\frac{\pi}{3}\beta(2)+\frac{\pi}{6} \\ \int_0^1 E(x) E'(x)^2 \, dx &=\frac{7}{576}A+\frac{5}{18}B+\frac{\pi^3}{24} \\ \end{align*}
現段階では$20$個の内$11$個示せているのでその証明を書いていきます。
まず、最初の$4$つの$K$のみの積分を示す。
前に示した等式
$$\int_{0}^{1}\frac{\mathrm{Im}f(\frac1x)}{x(1-tx)}dx=\pi f(t)$$
で$f(t)=t\kappa(t)^3$すると
\begin{align*}
\int_{0}^{1}\frac{\mathrm{Im}f(\frac1x)}{x(1-tx)}dx
&=\int_0^1\frac{\mathrm{Im}\Big(\sqrt{x}\big(\kappa(x)+i\kappa(1-x)\big)\Big)^3}{x^2(1-tx)}
\\&=\int_0^1\frac{3\kappa(x)^2\kappa(1-x)-\kappa(1-x)^3}{\sqrt{x}(1-tx)}dx
\\&=\pi t\kappa(t)^3
\end{align*}
$t=0$を代入して、整理すると
$$3\int_0^1\frac{\kappa(x)^2\kappa(1-x)}{\sqrt{x}}dx=\int_0^1\frac{\kappa(1-x)^3}{\sqrt{x}}dx$$
適切な置換と$\displaystyle\kappa(x)=\frac{2}{\pi}K(x)$を用いて
$$\int_0^1K(x)^2K'(x)dx=\frac13\int_0^1K'(x)^3dx=\frac13 A$$
前に示した$\mathrm{Landen}$変換を用いて
\begin{align*}
\int_0^1xK(x)^2K'(x)dx&=\int_0^1\frac{2\sqrt{x}}{1+x}K\left(\frac{2\sqrt{x}}{1+x}\right)^2K'\left(\frac{2\sqrt{x}}{1+x}\right)dx
\\&=\int_0^1(1-x)K(x)^2K'(x)dx
\\\int_0^1xK(x)^2K'(x)dx&=\int_0^1K(x)^2K'(x)dx=\frac16A
\end{align*}
よく用いる等式がある。以下、断りなく用いる。
$$\int_0^1xK(x)^aK'(x)^bE(x)^cE'(x)^ddx=\int_0^1xK(x)^bK'(x)^aE(x)^dE'(x)^cdx$$
適切な置換により示される。
\begin{align*}
\int_0^1xK(x)^3dx&=2\int_0^1\frac{1-x}{1+x}K\left(\frac{1-x}{1+x}\right)^3\frac{dx}{(1+x)^2}
\\&=\frac14\int_0^1K'(x)^3(1-x)dx
\\&=\frac14\int_0^1K'(x)^3dx-\frac14\int_0^1xK'(x)^3dx
\\&=\frac14\int_0^1K'(x)^3dx-\frac14\int_0^1xK(x)^3dx
\\\int_0^1K'(x)^3dx&=5\int_0^1xK(x)^3dx
\end{align*}
別の置換を用いて、
\begin{align*}
\int_0^1xK(x)^3dx&=-2\int_0^1\frac{2x}{x^2+1}K\left(\frac{2x}{x^2+1}\right)^3\frac{x^2-1}{(x^2+1)^2}dx
\\&=-4\int_0^1K(x^2)^3x(x^2-1)dx
\\&=2\int_0^1K(x)^3(1-x)dx
\\3\int_0^1xK(x)^3dx&=2\int_0^1K(x)^3dx
\end{align*}
よって、
\begin{align*}
\int_0^1K(x)^3dx&=\frac{3}{10}A
\\\int_0^1xK(x)^3dx&=\frac15A
\end{align*}
先ほど示した
$$\int_0^1xK(x)^2K'(x)dx=\frac16A$$
を用いる。
\begin{align*}
\int_0^1xK(x)^2K'(x)dx&=2\int_0^1\frac{1-x}{1+x}K\left(\frac{1-x}{1+x}\right)^2K'\left(\frac{1-x}{1+x}\right)\frac{dx}{(1+x)^2}
\\&=\frac12\int_0^1K(x)K'(x)(1-x)dx
\\&=\frac12\int_0^1K(x)K'(x)dx-\frac12\int_0^1xK(x)K'(x)^2dx
\\&=\frac12\int_0^1K(x)K'(x)dx-\frac12\int_0^1xK(x)^2K'(x)dx
\\\int_0^1K(x)K'(x)^2dx&=3\int_0^1xK(x)^2K'(x)dx
\\&=\frac1{2}A
\end{align*}
よって、
$$\int_0^1K(x)K'(x)^2dx=\frac12A$$
$K$のみの積分は全て示せた。
$A$の値を求める。
$$A=\frac{\Gamma\left(\frac14\right)^8}{128\pi^2}$$
証明
ルジャンドル多項式の直行性を用いて示す。\begin{align} A&=3\int_0^1K(x)^2K'(x)dx \\&=6\int_0^1xK(x)^2K'(x)dx \\&=3\int_0^1K\big(\sqrt{x}\big)^2K\big(\sqrt{1-x}\big)dx \\&=\frac{3\pi^3}{8}\sum_{n=0}^{\infty}\beta_n^4(4n+1)\int_0^1K\big(\sqrt{x}\big)P_{2n}(2x-1)dx \\&=\frac{3\pi^3}{8}\sum_{n=0}^{\infty}\beta_n^4(4n+1)\sum_{m=0}^{\infty}\frac1{2m+1}\int_0^1P_{m}(2x-1)P_{2n}(2x-1)dx \\&=\frac{3\pi^3}{8}\sum_{n=0}^{\infty}\beta_n^4(4n+1)\sum_{m=0}^{\infty}\frac1{(2m+1)(4m+1)}\delta_{2n,m} \\&=\frac{3\pi^3}{8}\sum_{n=0}^{\infty}\frac{\beta_n^4}{4n+1} \\&=\frac{\pi^6}{16\Gamma\left(\frac34\right)^8} \\&=\frac{\Gamma\left(\frac14\right)^8}{128\pi^2} \end{align}
$E$が含まれる積分を部分積分を用いて求める。
$\displaystyle x(1-x^2)K(x)^3$を微分する。
$$\frac{d}{dx}x(1-x^2)K(x)^3=-2K(x)^3+3K(x)^2E(x)$$
左辺を積分する。
\begin{align*}
\int_0^1\frac{d}{dx}x(1-x^2)K(x)^3dx&=\Big[x(1-x^2)K(x)^3\Big]_0^1
\\&=0
\\\int_0^1\frac{d}{dx}x(1-x^2)K(x)^3dx&=-2\int_0^1K(x)^3dx+3\int_0^1K(x)^2E(x)dx
\\\int_0^1K(x)^2E(x)dx&=\frac23\int_0^1K(x)^3dx
\\&=\frac15A
\end{align*}
よって、
$$\int_0^1 K(x)^2 E(x)dx=\frac15A$$
次からこの手法を用いるときは、微分する関数とそれを積分して導かれる関係式のみ書く。
$\displaystyle x(1-x^2)K'(x)^3$を微分して、積分することで
$$\int_0^1 K'(x)^2 E'(x) dx =\frac13A$$
$\displaystyle x(1-x^2)K(x)K'(x)^2$を微分して、積分することで
$$\int_0^1K'(x)^2E(x)dx=2\int_0^1K(x)K'(x)E'(x)dx$$
ルジャンドルの関係式を用いて積分を計算する。
\begin{align*}
&3\int_0^1K(x)K'(x)E'(x)dx-\int_0^1K(x)K'(x)^2dx
\\&\ \ =\int_0^1K'(x)^2E(x)dx+\int_0^1K(x)K'(x)E'(x)dx-\int_0^1K(x)K'(x)^2dx
\\&\ \ =\int_0^1K'(x)\big(K'(x)E(x)+K(x)E'(x)-K(x)K'(x)\big)dx
\\&\ \ =\frac{\pi}{2}\int_0^1K'(x)dx
\\&\ \ =\frac{\pi^3}{8}
\end{align*}
先ほど求めた値を用いて積分の値を求めると
\begin{align*}
\int_0^1K(x)K'(x)E'(x)dx&=\frac16A+\frac{\pi^3}{24}
\\\int_0^1K'(x)^2E(x)dx&=\frac1{3}A+\frac{\pi^3}{12}
\end{align*}
同様にして、
\begin{align*}
\int_0^1K(x)K'(x)E(x)dx&=\frac29A+\frac{\pi}{3}\beta(2)
\\\int_0^1K(x)^2E'(x)dx&=\frac19A+\frac{2\pi}{3}\beta(2)
\end{align*}
他の積分は、よくわからない。
$E$の$2$乗以上が積分に含まれていると、よくわからないっぽいです。
他にも、$x,x^2,x^3$が含まれる積分、さらにはもっと一般に$x^n$が含まれる積分を考えてみたいです。
例えば、以下のようなものがあるようです。上$2$つは示せています。
\begin{align}
\int_0^1xK'(x)^3dx&=\frac15A
\\\int_0^1x^2K'(x)^3&=\frac15-\frac{\pi^4}{40}
\\\int_0^1x^3K'(x)^3&=-\frac1{15}A+\frac{32}{15}B-\frac65
\end{align}
全て数値計算したわけではありませんが、おそらく全て
$$A,B,\pi^4,\pi^3,\pi^2,\pi,1,\pi\beta(2),\beta(4)$$
の$\mathbb{Q}$線形結合で表せられると思います。
証明の方針としてはまず、$1,x,x^2$が含まれる積分を示し、
この記事
のような方法を用いて$4$項間漸化式を導けばいいと思います。
もし、その$4$項間漸化式が解ければ、一般項を求めたことになります。
その漸化式ためにはまず微分方程式を求める必要があります。
$K(x)^3,K'(x)^3,E(x)^3$が満たす微分方程式を求める方法は分かっていますが、計算が面倒でまだ求めていません。
$K(x)E(x)E'(x)$が満たす微分方程式とか求められる気がしませんがね。
$4$乗以上の積分だとどうなるか気になりますね。
$3$乗だと上で書いた$10$個の定数の$\mathbb{Q}$線形結合から書けますが、$4$乗だと何個の定数の$\mathbb{Q}$線形結合で書けるのか気になりますね。
こうゆうの基底って言ったりするんですかね。
$3$乗以上の積分は、難しすぎる気がしますね。終わりです。
