平均曲率と閉超曲面の"半径"~Hasanis-Koutroufiotisの不等式~
以前 こちらの記事 で紹介させていただいた通り, 平均曲率の制限はしばしば曲面のサイズに制限を与えます. 今回は超曲面に対して成り立つ, 平均曲率と曲面のサイズの間の素朴な関係を示す幾何学的不等式であるHasanis-Koutroufiotisの不等式について紹介しようと思います.
$\Sigma^n \subset \mbb{R}^{n+1}$を閉超曲面($\mbb{R}^{n+1}$にはめ込まれた境界のない向きづけられたコンパクト多様体)とし, $H$を$\Sigma$の平均曲率とする. もし$\Sigma$が半径$R>0$のある球体$B_R(x)$に含まれるならば, $R\cdot\max_{\Sigma}|H| \geq 1$でなければならない. また等号成立は, $\Sigma$が半径$R=1/\max_{\Sigma}|H|$の$n$次元球面のときに限る.
今回は平均曲率$H$を, シェイプ作用素を$S$としたとき, $H = \tr{S} /n$で定義しています.
$\max_{\Sigma} |H|= 0$のときはどうなのかと気になった方がいるかもしれません. このとき$\Sigma$は境界を持たないコンパクトな極小超曲面となりますが, そのような極小超曲面は存在しない(詳しくは こちら を参照)ため, 今の設定では心配しているような状況は起こりません.
主張のイメージ
$H_0 = \max_{\Sigma}|H|>0$とおいて不等式を変形すると
\begin{align}
R \geq \frac{1}{H_0}
\end{align}
となるので「$\Sigma$を含むような球体の半径は少なくとも$1/H_0$でなければならない」というのが定理の主張です.
これは次の図ような状況をイメージするとわかりやすいかと思います.
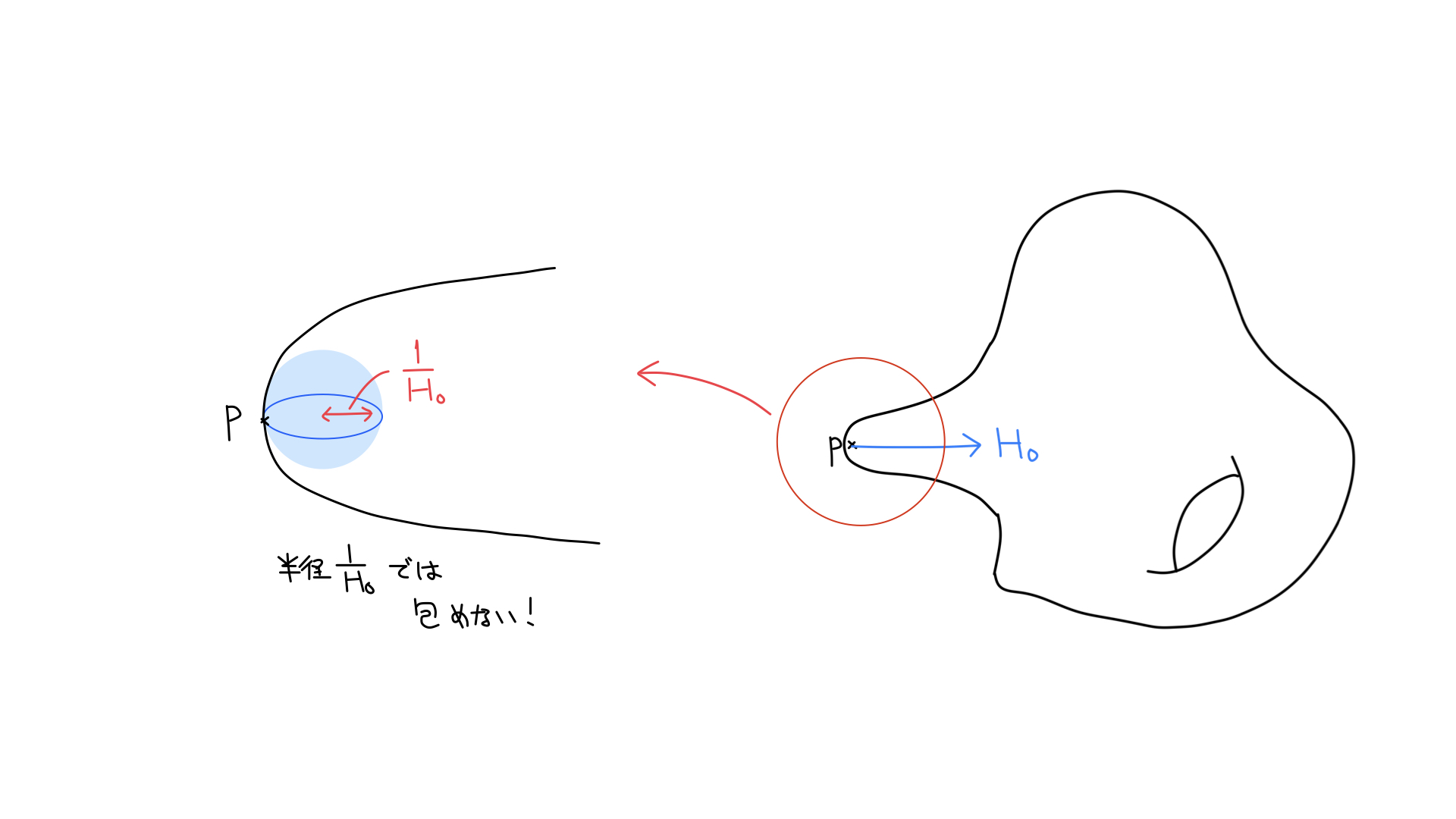強く曲がった部分に接する球体
$\Sigma$を含む最小の球体を考えると, その表面は$\Sigma$上のどこかで接します. 図で, 最も尖っている点$p$の平均曲率は, 半径$1/H_0$の球面の平均曲率と同じです. そこで, 球体が点$p$で接するような状況を考えると, 球体が$p$の周りの点を包むためには半径が$1/H_0$以上は必要そうです.
一方で上記の考察から, この半径の評価は非常にラフだということがわかります(冒頭ではこの意味で「素朴な関係」という紹介をしました). このことは次の図からもすぐにわかります.
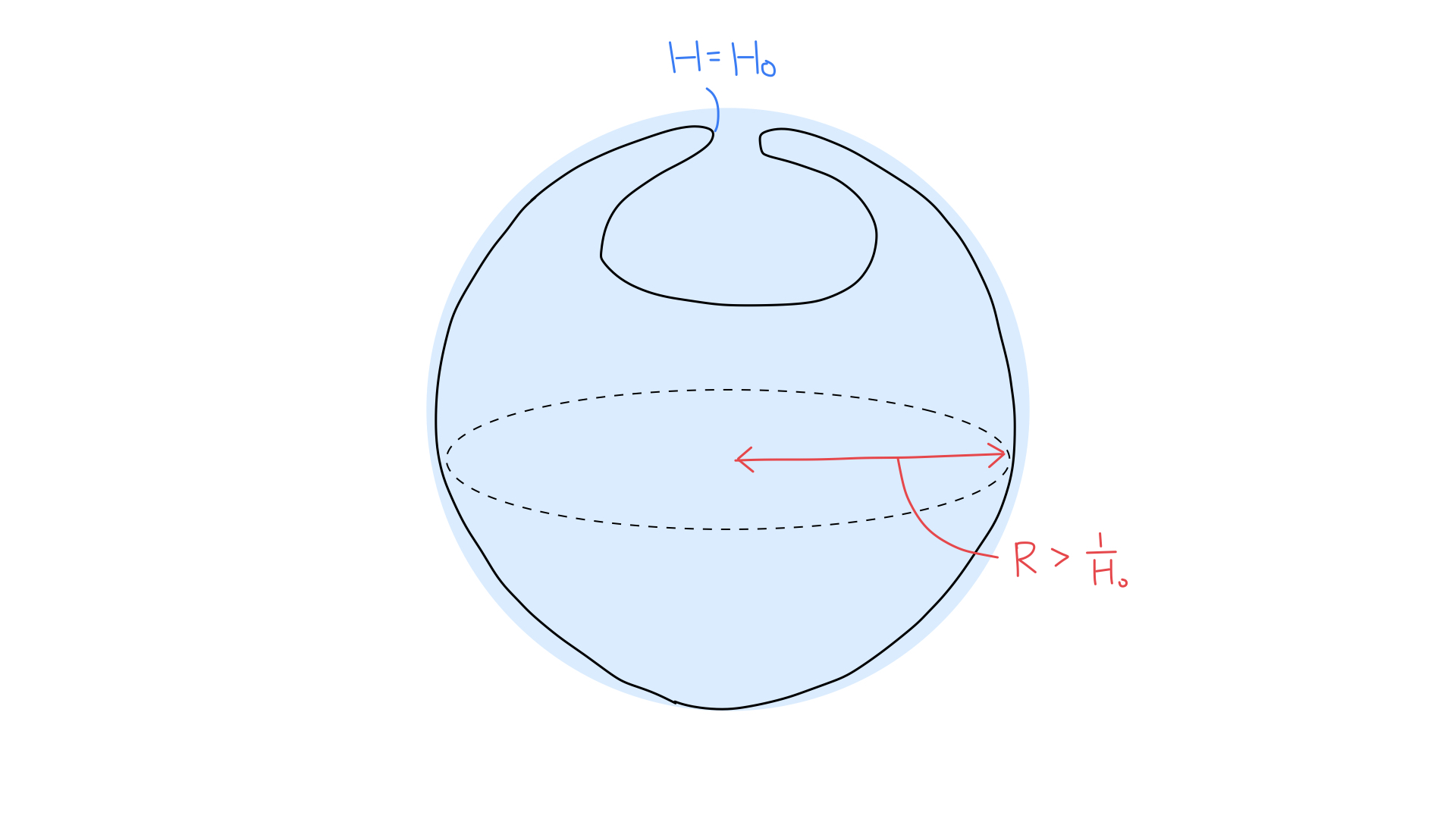角の生えた曲面とそれを包む球体
Hsiung-Minkowskiの公式
HasanisとKoutroufiotisによるオリジナルの論文HKでは, 最大値原理という楕円型偏微分方程式論の道具を用いて不等式が示されています. これ自体も幾何解析において(息をするように)用いられる重要なテクニックのひとつですが, 今回は偏微分方程式論の知識を仮定せず, 最低限の幾何学と関数解析の知識で理解できるよう, Hsiung-Minkowskiの公式と呼ばれる関係式を用いた証明を紹介します.
$X: \Sigma \to \mbb{R}^{n+1}$を閉超曲面とすると, 次の等式が成り立つ:
\begin{align}
\int_{\Sigma}(H\inn{N}{X} + 1) = 0.
\end{align}
第一変分公式
を用いて示す. はめ込み$X$の変分$X_t\,(|t|<\eps)$を
\begin{align}
X_t = (1+t)X
\end{align}
で定義する(相似拡大). $\Sigma_t = X_t(\Sigma)$とおくと, 第一変分公式より
\begin{align}
\left.\frac{d}{dt}\right|_{t=0}\vol{\Sigma_t} = -\left.\frac{d}{dt}\right|_{t=0}\int_{\Sigma}\inn{nHN}{(1+t)X}=-n\int_{\Sigma}\inn{HN}{X}.
\end{align}
一方, $\vol{\Sigma_t} = (1+t)^n\vol{\Sigma}$より,
\begin{align}
\left.\frac{d}{dt}\right|_{t=0}\vol{\Sigma_t} = n\vol{\Sigma}.
\end{align}
以上より,
\begin{align}
-n\int_{\Sigma}\inn{HN}{X} = n\vol{\Sigma}.
\end{align}
$\vol{\Sigma} = \int_{\Sigma}1$に注意すれば, 示したかった等式を得る.
超曲面の重心
証明に入る前に, 今回用いる記号の準備をします.
$p \geq 1$に対し, 閉超曲面$\Sigma$上の関数$f$の$L^p$ノルム$\|f\|_p$を
\begin{align}
\|f\|_p = \left(\frac{1}{\vol{\Sigma}}\int |f|^p \right)^{\frac{1}{p}}
\end{align}
で定義する.
また, 見やすさのため, $\Sigma$に沿ったベクトル場$V$に対し,
\begin{align}
\|V\|_p = \||V|\|_p
\end{align}
とおく.
はめ込み$X: \Sigma \to \mbb{R}^{n+1}$に対し,
\begin{align}
X_0=\frac{1}{\vol{\Sigma}}\int_{\Sigma}X
\end{align}
で表される点$X_0 \in \mbb{R}^{n+1}$を$\Sigma$の重心と呼ぶ. ここで, ベクトル場$X$の積分は, $X$の第$i$成分$(1 \leq i \leq n+1)$を$\Sigma$上の関数と思って成分ごとに積分し, その結果を並べたベクトルとして定義している.
重心をこのように定義するのには, これが剛体の重心の定義と同一なことに気づけば腑に落ちるかと思います.
超曲面の重心は, 超曲面$\Sigma$の慣性モーメントを最小化するという意味で, $\Sigma$の中心とでも呼ぶべき点になっています.
閉超曲面$\Sigma$の重心$X_0$は次を満たす:
\begin{align}
\|X-X_0\|_2 = \inf_{x \in \mbb{R}^{n+1}}\|X-x\|_2.
\end{align}
関数$I: \mbb{R}^{n+1} \to \mbb{R}$を$I(x)=\|X-x\|_2^2$で定める. 任意のベクトル$v\in \mbb{R}^{n+1}$に対し,
\begin{align}
dI_x(v) = \left.\frac{d}{dt}\right|_{t=0}I(x+tv) = \frac{1}{\vol{\Sigma}}\left.\frac{d}{dt}\right|_{t=0}\int_\Sigma |(X-x)-tv|^2 = \frac{2}{\vol{\Sigma}}\int_\Sigma \inn{X-x}{v} = \inn{\frac{2}{\vol{\Sigma}}\int_\Sigma (X-x)}{v}
\end{align}
となるので, $\nabla I(x)=\frac{2}{\vol{\Sigma}}\int_\Sigma (X-x)$. とくに, 重心$X_0$は$I$の臨界点である.
いま, 関数$x \mapsto |X-x|^2$の凸性から$I$も凸関数となるから, $I$の臨界値は$I$の最小値となる.
以上より, $\|X-X_0\|_2^2=I(X_0)= \inf_{x \in \mbb{R}^{n+1}}\|X-x\|_2. $
定理の証明
前節で導いた重心の性質を使って, まず$L^2$版の不等式を示します.
$X: \Sigma^n \to \mbb{R}^{n+1}$を閉超曲面とすると, 任意の$x \in \mbb{R}^{n+1}$に対し,
\begin{align}
\|H\|_2\|X-x\|_2 \geq 1
\end{align}
が成り立つ.
等号成立は, $x$が$\Sigma$の重心$X_0$であり, かつ$\Sigma$が$x=X_0$を中心とした半径$1/\|H\|_2$の$n$次元球面のときに限る.
Hsiung-Minkowskiの公式およびCauchy-Schwarzの不等式により
\begin{align}
1=\left|\frac{1}{\vol{\Sigma}}\int_\Sigma \inn{HN}{X-x} \right| \leq \frac{1}{\vol{\Sigma}}\int_\Sigma |H||X-x| \leq \|H\|_2\|X-x\|_2
\end{align}
特に, $\|X-u\|_2 \geq 1/\|H\|_2$となる.
よって, 等号が成立するとき, $x$は$\|X-x\|_2$を最小化するので, 重心の性質から$x=X_0$である.
さらに, Cauchy-Schwarzの不等式の等号成立条件から, $\Sigma$の各点で$X-X_0$は$N$と平行になる. このとき,
\begin{align}
\nablaS|X-X_0|^2=2\inn{X-X_0}{(X-X_0)^T}=0
\end{align}
となるので, $|X-X_0|=\mrm{const.}=r$.
また, $r=\|X-X_0\|_2=1/\|H\|_2$となるので, $\Sigma$は$X_0$を中心とした半径$1/\|H\|_2$の球面である.
$\Sigma\subset B_R(x)$となるとき,
\begin{align}
\|X-x\|_2 \leq \max_\Sigma |X-x| \leq R
\end{align}
となるので, 補題4より
\begin{align}
1 \leq \|H\|_2\|X-x\|_2 \leq \|H\|_2 R \leq R\cdot \max_\Sigma |H|
\end{align}
となる.
また, 補題4の等号成立条件から, 等号成立は$\Sigma$が重心を中心とした半径$R=1/\max_\Sigma |H|$の球面のときに限る.
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
