文献あり

蛇グラフ超入門（蛇の補題は関係ないよ）

465

こんにちは、ロダンです。今回は、最近注目されている新しい組み合わせ論の道具、「蛇グラフ」について紹介したいと思います。このグラフは正方形を名前の通り蛇のように連ねた図形であり、元々は団代数の団変数を計算するためにProppによってその原型が導入され、Musiker-SchifflerやMusiker-Schiffler-Williams1 Musiker-Schiffler-Williams2によってその理論が整備された概念です(Proppの出版は2020年ですが、プレプリントは2005年から存在しています)。近年では団代数の文脈を離れ純粋な組み合わせ論的な対象としても注目されているので、この機会に定義とその性質を簡単に紹介したいと思います。

蛇グラフの定義

さっそく定義をしていきましょう。次の符号付きタイルと呼ばれる2種類のタイルを並べていくことを考えます。
符号付きタイル

以下のルールにしたがってタイルを並べていきます。

最初のタイルは図1中の左のタイルを使う。
最初に置いたタイルの上か右のどちらかに、1辺を共有するようにして次の符号付きタイルを置く。
タイル同士の辺を共有している部分の符号は一致しているようにする。

この操作を有限回繰り返してできた図形、あるいはその符号を忘れたグラフのことを蛇グラフと呼びます。例えば図2の左の図はタイルをルールにしたがって並べたものであり、右の図はその符号を取り除いた蛇グラフです。

蛇グラフ

蛇グラフを構成する際、次のタイルを直前のタイルの上か右のどちらかに置く選択をしますが、これは言い換えれば直前のタイルの$+$と$-$のどちらを次のタイルと共有するかを選択しているということです。したがって、蛇グラフの形は内部にある符号$\{+,-\}$を左下から順に列挙した列で制御されているといえます。例えば図2で与えられているタイルたちの内部にある符号を左下から順に列挙すると$(+,+,-,-,-)$となっていますが、逆に符号列$(+,+,-,-,-)$を指定すると、この列をタイルたちの内部の符号として持つような蛇グラフは図2で与えられているものに一意的に決まります。この「一意的」は回転操作や鏡映操作による差を考慮していませんが、例えば符号列$(+,+,-,-,-)$の符号をすべて反転させた$(-,-,+,+,+)$から蛇グラフを作ると、これは$(+,+,-,-,-)$から作られる蛇グラフと鏡映の関係にあります（図3）。

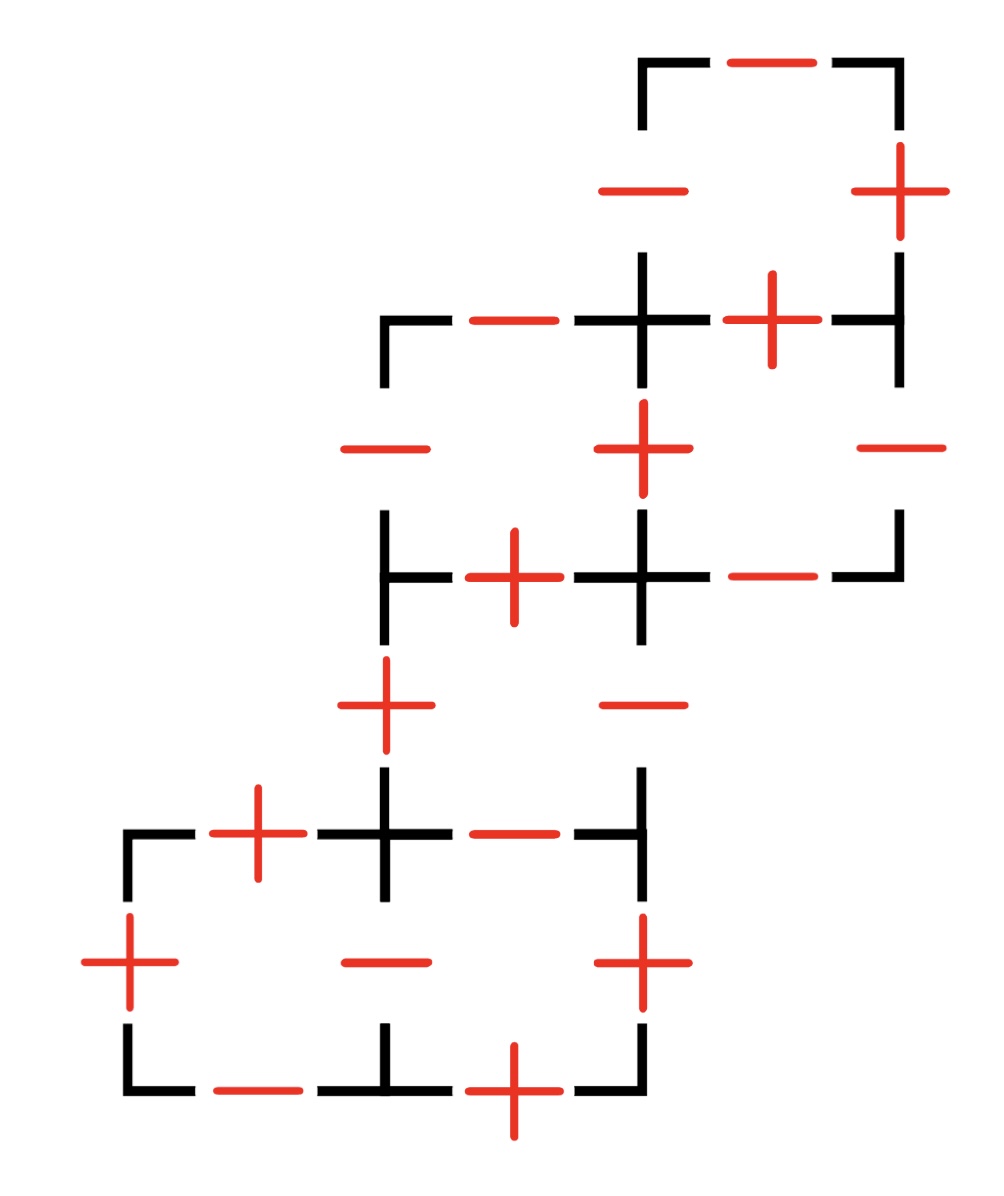鏡映の蛇グラフ

したがって、実は蛇グラフの「形」だけを制御するためには、符号列の情報よりももう少し弱く、「符号$+$と$-$が何回連続で続いているか」という情報を与える有限数列だけがあればOKです。この場合だと、数列$(2,3)$が蛇グラフの形を制御しているといえます。

ということで、この蛇グラフを数列$(2,3)$に付随する蛇グラフとして定義…したいところですが、そうはしません。ここでは、符号列$(+,+,-,-,-)$の最初と最後に符号を付け加えた符号列$(\varepsilon_1,+,+,-,-,-,\varepsilon_2)$（ただし$\varepsilon_1,\varepsilon_2\in\{+,-\}$）から定まる数列で図2の蛇グラフを定めます。すなわち、4つの数列$(1,2,3,1),(3,3,1),(1,2,4),(3,4)$のすべての数列に対して、これに付随する蛇グラフを図2で与えられるグラフとして定義します。数列が先に与えられている形で述べると、次のような定義になります。

有限な数列$(a_1,a_2,\dots,a_\ell)$（ただし$a_i\in \mathbb Z_{> 0}$）が与えられたとき、

$(a_1,\ell)\neq (1,1),(2,1)$ならば、$-$が$a_1$回連続で続いた後$+$が$a_2$回続き、また$-$が$a_3$回続き…となるような符号列$(s_1,s_2,\dots,s_n)$ （ただし$s_i\in \{+,-\}$であり、$n=\sum_{i=1}^\ell a_i$）を考える。内部の符号を左下から順に列挙した符号列が$(s_2,\dots,s_{n-1})$になるような蛇グラフを、数列$(a_1,a_2,\dots,a_\ell)$に付随する蛇グラフとよび、$\mathcal G(a_1,\dots,a_\ell)$とかく。
$(a_1,\ell)= (1,1)$ならば、2つの頂点とその間を結ぶ辺からなるグラフを考え、これを数列$(1)$に付随する蛇グラフと呼び、$\mathcal G(1)$とかく。
$(a_1,\ell)= (2,1)$ならば、図1の左のタイル1つからなるグラフを考え、これを数列$(2)$に付随する蛇グラフと呼び、$\mathcal G(2)$とかく。

(2)と(3)は数列から蛇グラフが作れない場合の例外処理です。この定義によれば、$\mathcal G(1,2,3,1), \mathcal G(3,3,1),\mathcal G(1,2,4),\mathcal G(3,4)$はすべて図2の蛇グラフ（を合同変換したもの）を指します。なぜこのようなまわりくどい定義をするのかについては一旦置いておいて、この蛇グラフを使って何をするのかについて踏み込んでいくことにしましょう。

蛇グラフの完全マッチングの個数

この記事では、与えられたグラフ$G$を、その頂点集合$V$と辺集合$E$を使って$G=(V,E)$のように表すとします。以下、蛇グラフの各タイルの角の全体集合を頂点集合$V$、角を結ぶ辺全体を辺集合$E$とします。組み合わせ論において、グラフが与えられた時にまず考えたいのはその完全マッチングでしょう（私の偏見かもしれませんが）。

グラフ$G=(V,E)$が与えられたとき、$E$の部分集合であって次の条件を満たすもの$P$を$G$の完全マッチングという：$V$の任意の元$v$に対して、ある$P$の元$e$が一意的に存在して、$e$の端点の1つが$v$となる。

グラフの形状によってはこの完全マッチングが存在しないようなグラフもあります（例えば頂点が奇数個の連結なグラフ）が、蛇グラフではそのようなことは起こりません。また、完全マッチングは1種類とは限りません。たとえば、$\mathcal G(1,2,3,1)$には以下の13種類の完全マッチングが存在します（赤で示した辺が完全マッチングに属する辺を指しています）。

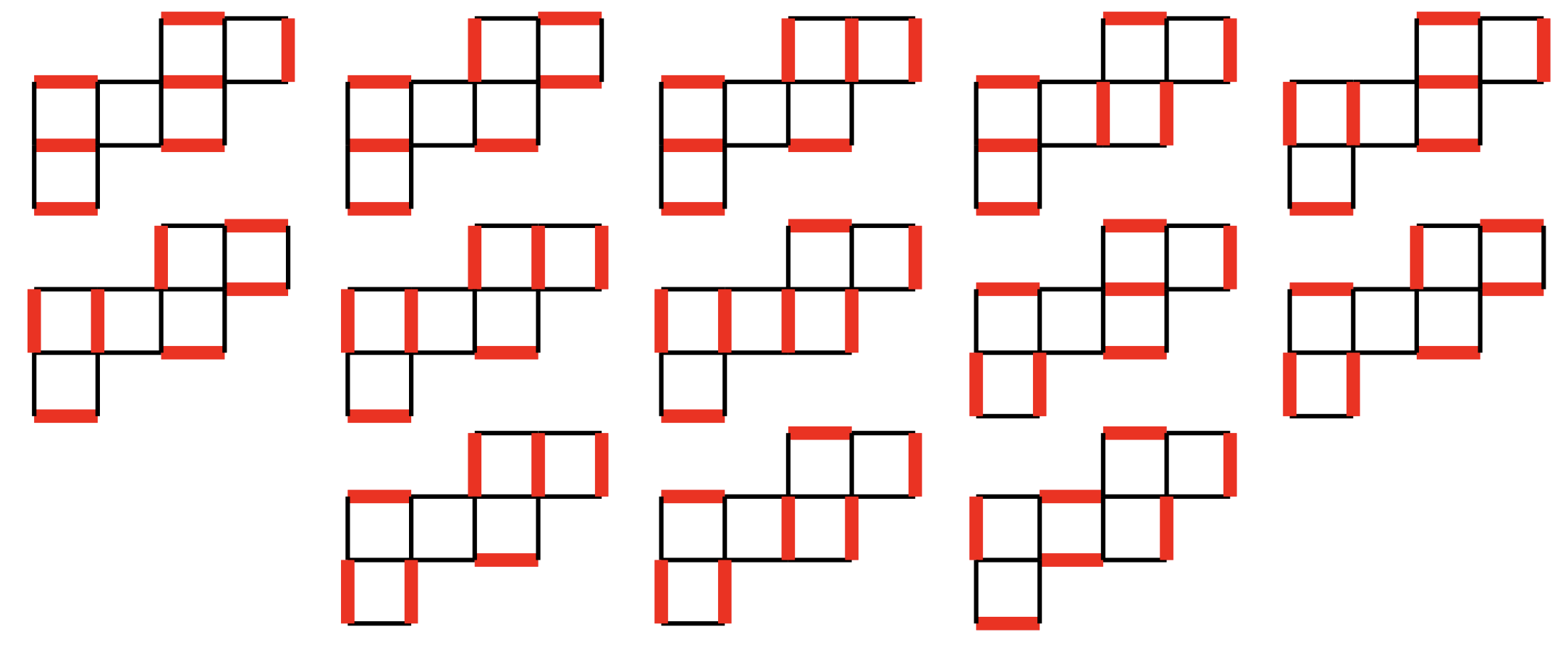完全マッチング一覧

特にこの完全マッチングの個数に注目します。一般にグラフ$G$が与えられたとき、その完全マッチングの個数がいくつかを数えるのは難しい問題です。一番安直なのは図4のように重複なくすべて列挙することだと思いますが、手作業でやろうとするとグラフが大きい場合に重複してないかどうかの確認がかなり面倒になると思います。わたしは図4程度の全列挙でももう2度とやりたくありません。
もしこの個数が計算で簡単に求められるのであれば嬉しいわけですが、実はグラフが蛇グラフの場合はそれができるのです。蛇グラフ$\mathcal G(a_1,\dots,a_n)$の完全マッチングの個数を$N(a_1,\dots,a_n)$で表すことにします。また、$[a_1,\dots,a_n]$で連分数
\begin{align} [a_1,\dots,a_m]:=a_1+\dfrac{1}{a_2+\dfrac{1}{\ddots+\dfrac{\ddots}{a_{m-1}+\dfrac{1}{a_m}}}} \end{align}
を表すことにします。このとき、以下の定理が成り立ちます。

[1, Theorem 3.4]

以下の等式が成立する：
\begin{align} [a_1,\dots,a_n]=\dfrac{N(a_1,\dots,a_n)}{N(a_2,\dots,a_n)}. \end{align}
なお、右辺は既約分数となる。ただし、$N(\ )=1$と定義する。

定理1によれば、$\mathcal G(1,2,3,1)$の完全マッチングの個数を知りたければ連分数$[1,2,3,1]=1+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{1}}}$を計算してその分子を見ればいいようです。実際に計算して見ると$\dfrac{13}{9}$となり、その分子は確かに直接完全マッチングを全列挙して確かめた$N(1,2,3,1)=13$に一致していることがわかります。蛇グラフを定義する時にわざわざ内部の符号ではなくその両端に符号を付け足した数列と対応させた理由の1つはここにあります。

…すごくないですか？僕はこれを知ったときめちゃくちゃ驚きました。完全マッチングの数なんてそう簡単に数え上げられるものじゃないように見えるのですが、連分数を使ってこんなあっさり計算できてしまうんです。ちなみに、この性質から連分数に関して例えば次のようなことがわかります。

定理1

連分数$[a_1,\dots,a_\ell]$と$[1,a_1-1,\dots,a_\ell]$を既約分数表示したときの分子は等しい。
連分数$[a_1,\dots,a_\ell]$と$[a_1-1,\dots,a_\ell-1,1]$を既約分数表示したときの分子は等しい。
連分数$[a_1,\dots,a_\ell]$と$[a_\ell,\dots,a_1]$を既約分数表示したときの分子は等しい。

いずれも、前者と後者の数列から同じ形の蛇グラフを与えることと定理1を使って示すことができます（もちろん蛇グラフを使わずに直接的に証明することもできます）。

これらの話だけでもだいぶ面白いと僕は思っていますが、まだ話は続きます。

蛇グラフと平方和

前節の定理により蛇グラフの完全マッチングの数を簡単に計算できるようになったわけですが、まだ「蛇グラフの完全マッチングの数を知ることでなんの役に立つのか」という部分に言及していないので、ここからはその話をしていくことにします。本稿のこれ以降の話についてはCanakci-Schiffler2により詳しいことが書いてあります。

まず、蛇グラフの完全マッチングの数について、次の定理が成り立つことが知られています。

[1, Theorem 5.2]

数列$(a_1,\dots,a_\ell)$と任意の$i\in\{2,\dots,\ell-1\}$について、次の等式が成り立つ:
\begin{align} N(a_1,\dots,a_\ell)=N(a_1,\dots,a_i)N(a_{i+1},\dots,a_\ell)+N(a_1,\dots,a_{i-1})N(a_{i+2},\dots,a_\ell). \end{align}

この定理は蛇グラフ$\mathcal G(a_1,\dots,a_\ell)$の完全マッチングの数え方を工夫することで証明することができます。一般の場合で書くと証明が長くなるので、ここでは数列が$(a_1,a_2,a_3,a_4)=(2,1,3,2)$のときの$i=2$のケースに沿って大体の証明方針を与えることで納得してもらうことにします。

!FORMULA[78][-1967409691][0] $\mathcal G[2,1,3,2]$
まず、$\mathcal G[2,1,3,2]$の完全マッチングのうちの左2つのタイルの完全マッチングとと右4つのタイルの完全マッチングに分離できるケースを考えます。例えば、以下の完全マッチングはそのような例です。
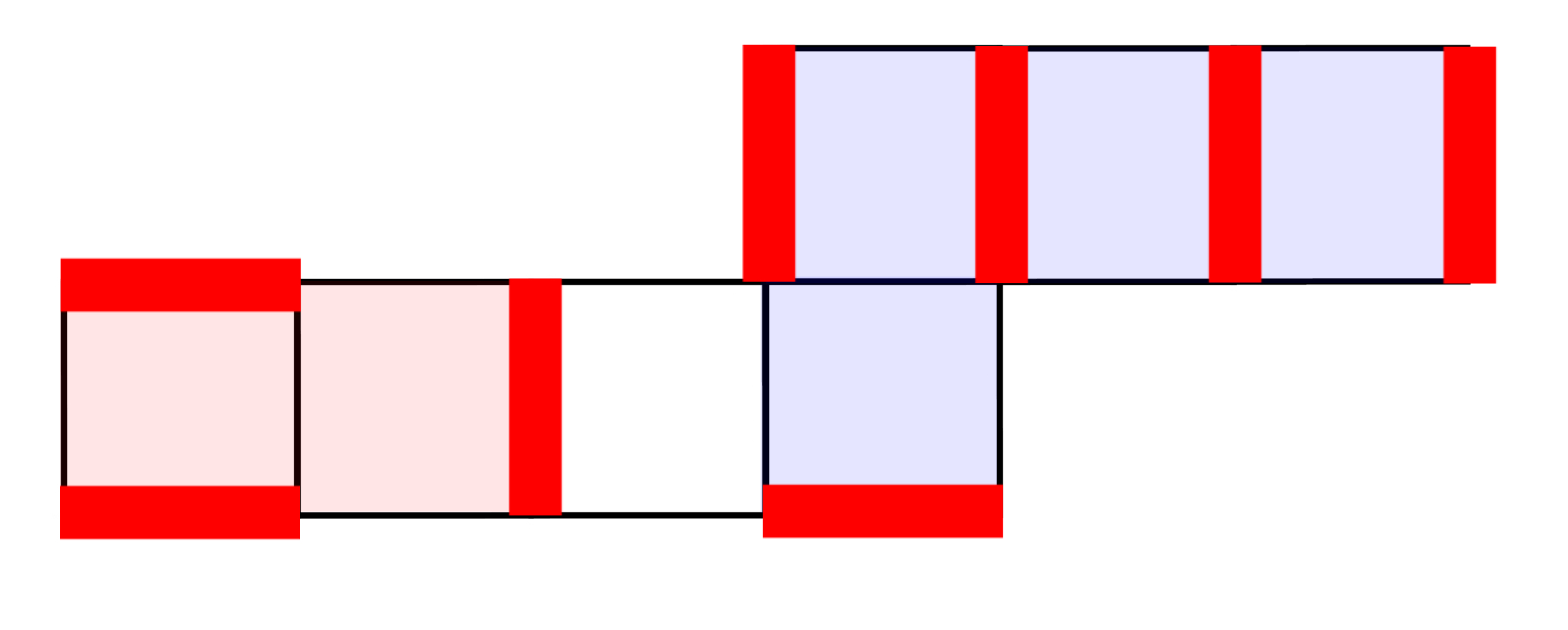分離される例
この完全マッチングに含まれる辺（赤い太線）は、赤い2つのタイルの完全マッチングまたは青い4つのタイルの完全マッチングの辺としてもみれることがわかると思います。このタイプの完全マッチングは、赤いタイルの図形が$\mathcal G(2,1)$、青いタイルの図形が$\mathcal G(3,2)$としてみれることから、全部で$N(2,1)N(3,2)$個あることがわかります。では、これ以外の完全マッチングは全部でいくつあるでしょうか？そのような完全マッチングは、少なくとも図6中の白いタイルの上下の辺の少なくともどちらかを含んでいなければなりません。実は、どちらかの辺を含んでいるときはもう片方も含んでいないと完全マッチングにならないことがわかります（チェックしてみましょう）。加えて、少なくとも図7に赤で示されるような辺は全て含んでいなければなりません。
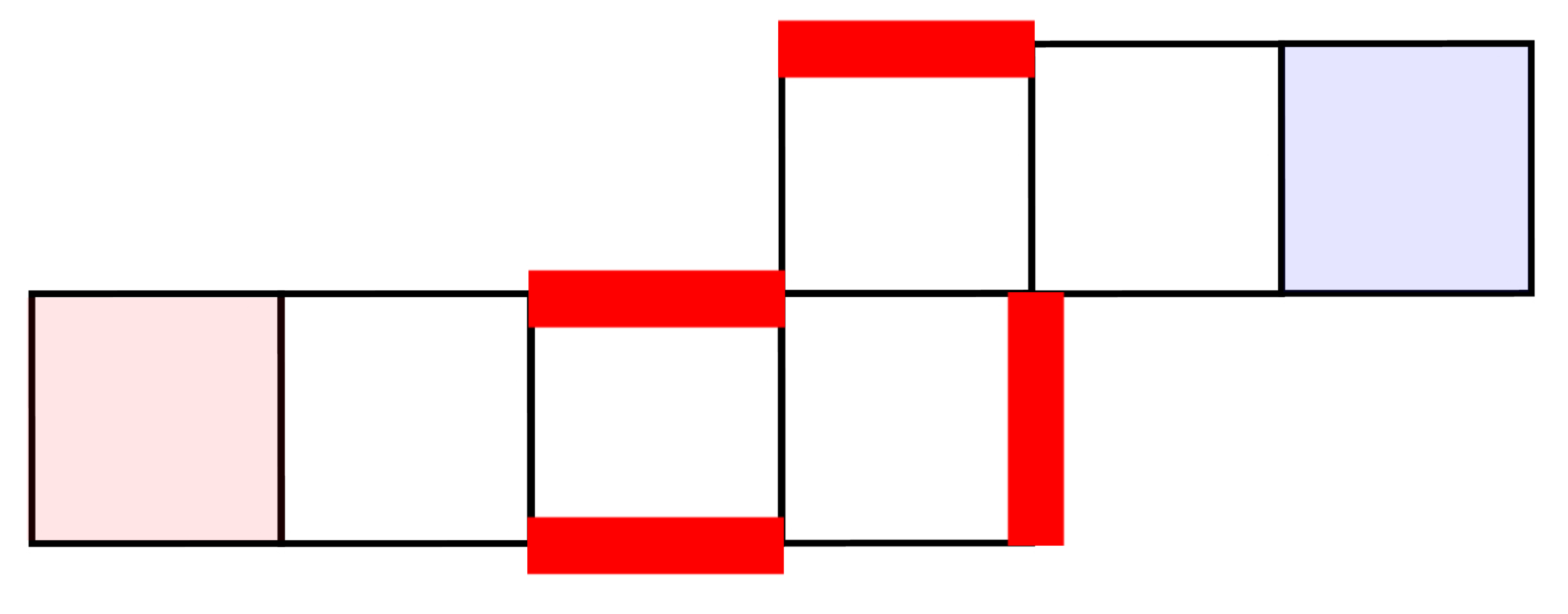含まれていなければいけない辺
したがって、図7のケースでは同図中の赤いタイルと青いタイルにおける完全マッチングが決まれば全体の完全マッチングが決定されることになり、その完全マッチングの数は$N(2)N(2)$で与えられます。以上で、

\begin{align} N(2,1,3,2)=N(2,1)N(3,2)+N(2)N(2) \end{align}
が示されました。一般のケースでも、$a_1,a_2,\dots,a_\ell$の値と$i$の値に応じて図6の白いタイルにあたるタイルを決定し、同様の議論で証明することが可能です。

定理2は、特に$N(a_1,\dots,a_{i})=N(a_{i+1},\dots,a_{\ell})$かつ$N(a_1,\dots,a_{i-1})=N(a_{i+2},\dots,a_{\ell})$であるような$i$が取れるケースが興味深いです。これが成り立つ例としては数列$(a_1,\dots,a_\ell)$に対して$\ell$が偶数で、かつ$ a_1,\dots,a_\ell$が回文的である場合が代表的です。ここで、数列が回文的であるとは、数列が逆から読んでも同じ数列になること、すなわち任意の$j$に対して$a_j=a_{\ell+1-j}$であることを意味します。この場合、$i=\dfrac{\ell}{2}$とすることで
\begin{align} N(a_1,\dots,a_{\frac{\ell}{2}})=N(a_{\frac{\ell}{2}},\dots,a_1)=N(a_{\frac{\ell}{2}+1},\dots,a_{\ell}) \end{align}
かつ
\begin{align} N(a_1,\dots,a_{\frac{\ell}{2}-1})=N(a_{\frac{\ell}{2}-1},\dots,a_1)=N(a_{\frac{\ell}{2}+2},\dots,a_{\ell}) \end{align}
となります。これをまとめると、以下が成り立つことがわかります。

定理2

数列$(a_1,\dots,a_\ell)$について、$\ell$が偶数かつ$ a_1,\dots,a_\ell$が回文的であるとき、\begin{align} N(a_1,\dots,a_\ell)=N(a_1,\dots,a_{\frac{\ell}{2}})^2+N(a_1,\dots,a_{\frac{\ell}{2}-1})^2 \end{align}
が成立する。

定理1から$N(a_1,\dots,a_{\dfrac{\ell}{2}})$と$N(a_1,\dots,a_{\frac{\ell}{2}-1})$が互いに素であることに注意してください。例えば、$\mathcal G(1,2,2,1)$は次のようなグラフになります。 !FORMULA[105][957890498][0] $ \mathcal G(1,2,2,1)$
このとき、$[1,2,2,1]=\dfrac{10}{7}$なので定理1から$N(1,2,2,1)=10$ですが、この数は$N(1,2)=3, N(1)=1$であり、定理2の系から$10=3^2+1^2$と互いに素な2つの数の平方和でかけます。

マルコフ数への応用

マルコフ数は、蛇グラフの完全マッチングに現れる数の典型例です。私の記事をいろいろ読んでくださっている人からするとまたその話かよと思われるかもしれませんが、今一度マルコフ数について復習しておきましょう。マルコフ数とは、マルコフ方程式
\begin{align} x^2+y^2+z^2=3xyz \end{align}
の正整数解$(x,y,z)$に現れる正整数のことを指します。例えば$(x,y,z)=(1,5,2)$はこの方程式の正整数解なので、$5$はマルコフ数です。まず、これらの数たちがある蛇グラフの完全マッチングの数になることを説明します。この記事やこの記事でも実質的に全く同じ話をしていますが、この記事でも改めて紹介します。

正の既約分数$t\in(0,1]$をとり、固定します。まず、傾きが$t$の線分$L_t$を$x$軸と$y$軸を固定した平面$\mathbb R^2$上にとります。ここで、この線分$L_t$の端点はどちらも整数格子点上にあって、$L_t$はそれ以外の整数格子点を通らないようなものとします。そして、整数格子点を頂点に持つ長さ1の正方形であって$L_t$が通るものを全て取り出し、その全ての正方形の左上から右下にかけて対角線を引きます。ここまでで、例えば$t=2/5$のときは下図のような図形が描けています。
!FORMULA[124][969246841][0]のプレ蛇グラフ $t=2/5$のプレ蛇グラフ
この図形のことを、$t$のプレ蛇グラフといいます。次に、このプレ蛇グラフの各パーツに次のルールで符号$\{+,-\}$を配置します。まず、線分$L_t$に左下から右上方向への向きを定めておきます。

プレ蛇グラフを分割する各直角三角形に対して、

次の条件を満たす直角三角形に$-$を配置する(図10を参照)。
1. 線分$L_t$が左下の端点を共有している直角三角形
2. $L_t$の進行方向の向かって左側が四角形に分割されるような直角三角形　
  $-$を配置する三角形
次の条件を満たす直角三角形に$+$を配置する(図11を参照)。
1. 線分$L_t$が右上の端点を共有している直角三角形
2. $L_t$の進行方向の向かって右側が四角形に分割されるような直角三角形　
  $+$を配置する三角形

以上のルールに従って$t=2/5$のプレ蛇グラフに符号を配置すると次のような図を得ます。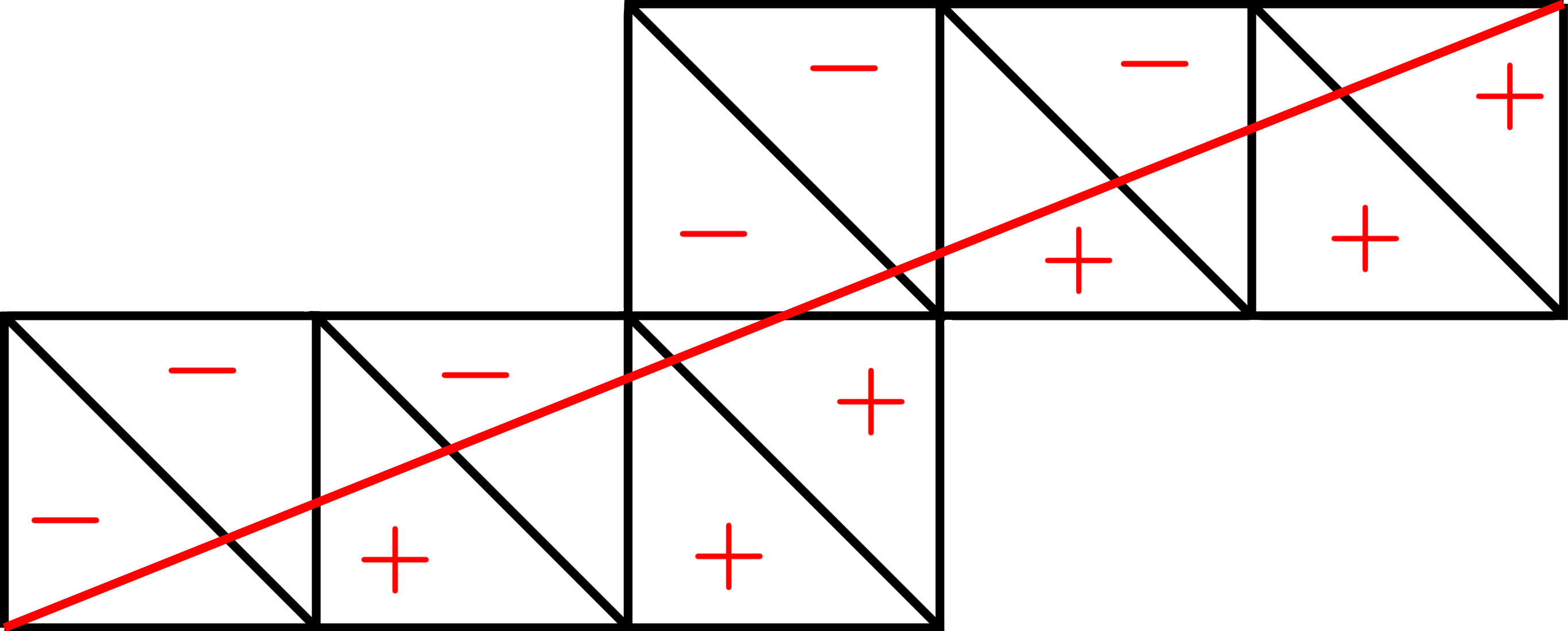符号つきプレ蛇グラフ
この符号を、線分$L_t$が左下から右上に向かって通る順番に並べます。たとえば、$t=2/5$の例では$-,-,+,-,+,+,-,-,+,-,+,+$です。この符号列、もしくはここから定まる有限数列から蛇グラフを構成します。この蛇グラフを$\mathcal G_t$と書くことにしましょう。$t=2/5$の例では$\mathcal G_{2/5}=\mathcal G(2,1,1,2,2,1,1,2)$です。ここで、$N_t$で$\mathcal G_t$の完全マッチングの数を表すとすると、次の定理が成立します。

[6, Theorem 7.1]

既約分数$t\in(0,1]$に対して、$N_t$はマルコフ数である。また逆に、$1$を除く全てのマルコフ数$m$に対して$m=N_t$となるような既約分数$t\in(0,1]$が存在する。

実際、$\mathcal G_{2/5}=\mathcal G(2,1,1,2,2,1,1,2)$の完全マッチングの個数を計算してみると、$[2,1,1,2,2,1,1,2]=\dfrac{194}{75}$なので$N_{2/5}=194$ですが、一方で$(5,13,194)$はマルコフ方程式の解なのでこれは確かにマルコフ数です。なお、定理3において$m=N_t$となるような既約分数$t\in(0,1]$が一意的かどうかは未解決です（マルコフ予想）。

また、$\mathcal G_t$の構成方法から次が成立します。

任意の既約分数$t\in(0,1]$に対して、$\mathcal G_t=\mathcal G(a_1,\dots,a_\ell)$であるとき、$\ell$は偶数かつ$(a_1,\dots,a_\ell)$は回文的である。

さらに命題4と定理2系から、次が従います。

任意のマルコフ数$m$に対して、互いに素な$\alpha,\beta$の組が存在して$m=\alpha^2+\beta^2$と表すことができる。

例えば$t=2/5$に対応するマルコフ数$194$を考えると、この数を完全マッチングの数として持つ回文的な蛇グラフとして$\mathcal G(2,1,1,2,2,1,1,2)$が取れるので、$194=N(2,1,1,2)^2+N(2,1,1)^2=13^2+5^2$となって確かに互いに素な2つの数の平方和としてとることができます。これは以前記事を書いたマルコフ数が互いに素な整数の2乗和でかけることの証明における定理1の別証明になっています。
あちらの記事の定理1では$\alpha,\beta$が$m$を含むマルコフトリプル$(a,b,m)$の取り方に依存していますが、こちらの$\alpha,\beta$は既約分数$t$の取り方に依存しています。$t$を1つ与えると、$t$が分数として大きさが2番目であるようなファレイトリプル$(r,s,t)$がとれ（ファレイトリプルの定義はこの記事を参照）、さらにそれに対応するマルコフ方程式の解$(N_r,N_s,N_t)$をとることができます。$t$が2番目の大きさであるようなファレイトリプル$(r,s,t)$の取り方は$t$に対して一意的なので、$(N_r,N_s,N_t)$も一意に決まり、さらに$N_r,N_s< N_t$が成立するのですが、$N_r=a,N_s=b$としたときに、この定理5で与えられる$\alpha,\beta$と別記事の定理1で与えられる$\alpha,\beta$が同じものになるかどうかはわかっていません。最後にこれを問題としてぶん投げて今回の締めとしたいと思います。