大学数学基礎解説

文献あり

ドミノで繋がる数学の話

日曜数学アドベントカレンダー,線形代数,ドミノタイリング

734

はじめに

　この記事は日曜数学 Advent Calendar 2023 の $10$ 日目の記事です。

　前日はコロちゃんぬさんの最大公約数と最小公倍数の分配法則についてでした。

　この記事では、私にとって今一番熱い話題である「ドミノタイリング」について語りたいと思います。

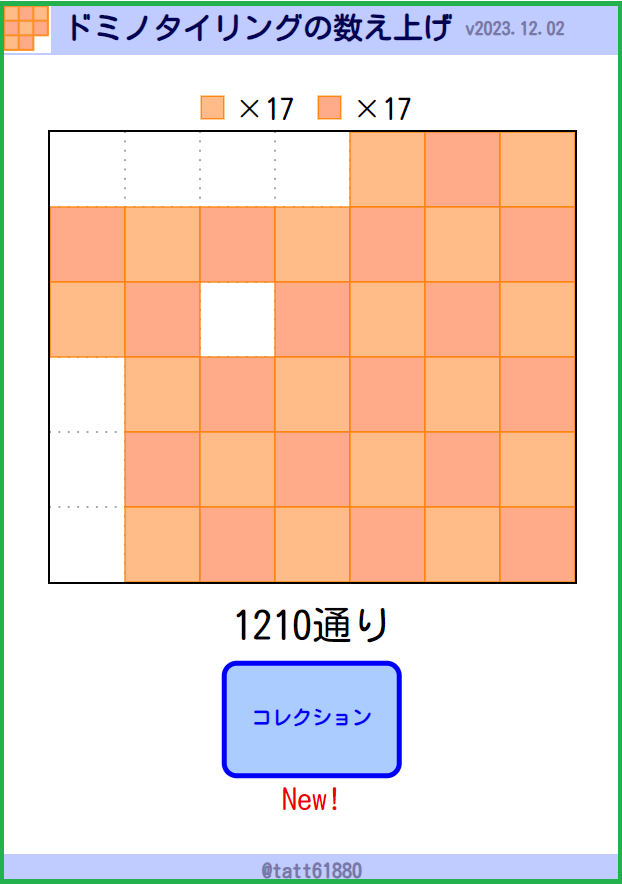今日の日付、12月10日にちなんだ1210とおりのドミノ数え上げパターン

ドミノタイリングとは

　ドミノタイリングというのは、図1 のようにしてドミノ($1\times2$ の長方形)で領域を埋めつくすことをいいます。

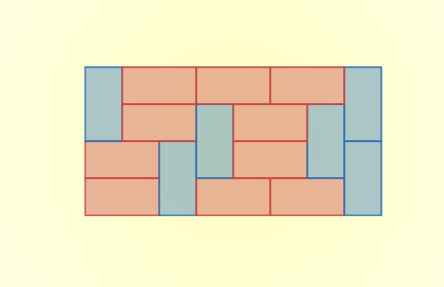ドミノタイリングの例

　これに興味を持ったきっかけは濱中裕明@Ototo_さんから2023年7月23日にもらったこのリプライでした。

縦横の長さが自然数の長方形に、1x2のドミノを敷き詰める場合の数を求める式も、cosがバンバンでてきます。っていうか、このトピックの元の問題もそこからかな。＞カステレイン行列
— 濱中裕明 (@Ototo_) July 22, 2023

　これをきっかけにして、$2023$ 年の後半、通勤時間や土日の日曜数学活動としてドミノタイリングと延々触れ合う日々が始まることになろうとは、このときは思いもよらなかったのでした。

ドミノタイリングの総数を求める公式に $\cos$ がたくさん出てくる話

　さて、さきのリプライに出てきた式はこういうものでした。

${\displaystyle m\times n}$ の長方形を ${\displaystyle 1\times 2}$ のドミノで埋め尽くす方法が何通りあるかの個数の公式

　${\displaystyle 　Z_{m,n}=\prod_{j=1}^{\left\lceil\frac{m}{2} \right\rceil}\prod_{k=1}^{\left\lceil\frac{n}{2} \right\rceil} 　\left( 　4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1} 　\right)}$

　いやあ、実に面白い式ですね!三角関数の $\cos$ が出てきています。$\prod$ は掛け算ですから、三角関数の式をたくさん掛け合わせています。にもかかわらず、答えが整数になる、というだけでも驚きですが、この式で${\displaystyle m\times n}$ の長方形を ${\displaystyle 1\times 2}$ のドミノで埋め尽くす方法が何通りあるかわかるというのですから!
　見た目もシンプルにまとまっていて実に美しいではありませんか!

　私はこの式をどうしても理解したいと思い、「線形代数と数え上げ[増補版]」の本Tを買ってしまったのでした。

　本を読んで、よくわからなかったところを自己流で補間することで、最終的にこの式を導出することに成功したのでした。
　そして、その導出方法と、なぜその式でドミノタイリングの総数を計算できるかについて記事にまとめました。
　前編記事ができたのが $10$ 月 $1$ 日、後編記事ができたのが $10$ 月 $21$ 日のことでした。

≪リンク≫ ドミノタイリングの数え上げ公式の導出方法【前編～導出～】
≪リンク≫ ドミノタイリングの数え上げ公式の導出方法【後編～証明～】

　式に出会ってから証明が完成するまで $2$ か月以上かかってますね・・・。
　ちょうど転勤して忙しくなり、平日は疲れ切って通勤時間も日曜数学活動はほとんどできていなかったこともあり、進捗は良くなかったと思います。
　しかし、時間を気にしなくていいのが日曜数学のいいところでもありますね。

任意のポリオミノをドミノで埋め尽くす総数を計算するアルゴリズムを作った話

　さて、証明記事が完成したとき、ふと「この方法を使えば、長方形でなくても、任意のポリオミノをドミノで埋め尽くす方法の総数を計算できるんじゃね?」と思いついたのでした……が。

　実際にやってみると、計算が合わない場合が出てきてしまいました。
　少し悩みましたが、「ポリオミノに穴が開いていたらそれも計算にいれなければいけない」ということを見落としていたことに気が付いたおかげで、少し修正することで、ほぼ同じ方法で任意のポリオミノバージョンも作ることができたのでした!
　修正できたのは $10$ 月 $26$ 日のことでした。
　この成果は、 $10$ 月 $29$ 日の日曜数学会で発表したのでした。振り返ってみると、発表の $3$ 日前に完成したんですね、我ながらギリギリすぎますね💦。
　その後、$11$ 月 $4$ 日に加筆記事を公開しました。

#日曜数学会
ドミノ埋め尽くしの総数と行列式の不思議な関係
発表スライド
1～4 /12 pic.twitter.com/5B6upw5GEH
— ａｐｕ (@apu_yokai) October 29, 2023

≪リンク≫ 任意のポリオミノをドミノで埋め尽くす方法の総数を行列式を使って求める方法(日曜数学会)

ドミノタイリングと平方剰余の関係についての論文が出た話

　それから間もない $11$ 月 $22$ 日、またドミノタイリングの式が話題になりました。なんと、平方剰余に関する式との関連がわかったというのです!

≪リンク≫ togetter:J.Koizumi氏による、平方剰余とドミノタイリングを結びつける公式を発見についての、中澤俊彦さんと神尾悠陽さんとの共著論文についての解説
≪リンク≫ arxiv:Quadratic residues and domino tilings

　その内容を少し解説します。
　$19$ 世紀ドイツの数学者アイゼンシュタインは奇素数 $p,q$ に対するルジャンドル記号 $\left(\frac{q}{p}\right) $ の値が以下のような式で表されることを示したといいます。

アイゼンシュタインによる奇素数 $p,q$ のルジャンドル記号

　${\displaystyle 　\left(\frac{q}{p}\right)=\prod_{j=1}^{\frac{p-1}{2} }\prod_{k=1}^{\frac{q-1}{2} } 　\left( 　4\cos^2\frac{2\pi j}{p}-4\cos^2\frac{2\pi k}{q} 　\right)}$

ルジャンドル記号についてはここをクリック / タップ

　ルジャンドル記号というのは、$p$ を奇素数、$a$ を $p$ と互いに素な $0$ でない整数として、

　${\displaystyle 　\left(\frac{a}{p}\right) 　\equiv a^{\frac{p-1}{2}}\qquad \mod p }$

になるもので、$-1,0,1$ のいずれかの値をとります。

　一方で、奇数 $m,n$ に対する $(m-1)\times(n-1)$ の長方形をドミノで埋め尽くす方法の総数は、先の公式の $m,n$ を $m-1,n-1$ で置き換えることで次のようになります。

奇数 $m,n$ に対して ${\displaystyle m-1\times n-1}$ の長方形を ${\displaystyle 1\times 2}$ のドミノで埋め尽くす方法が何通りあるかの個数

　${\displaystyle 　Z_{m-1,n-1}=\prod_{j=1}^{\frac{m-1}{2} }\prod_{k=1}^{\frac{n-1}{2}} 　\left( 　4\cos^2\frac{\pi j}{m}+4\cos^2\frac{\pi k}{n} 　\right)}$

　$m,n$ が奇数のときは、 $\cos$ の中の分子を $2\pi j,2\pi k$ に置き換えても総積に変わりないことが少し考えればわかりますので、置き換えると

奇数 $m,n$ に対して ${\displaystyle m-1\times n-1}$ の長方形を ${\displaystyle 1\times 2}$ のドミノで埋め尽くす方法が何通りあるかの個数(別表現)

　${\displaystyle 　Z_{m-1,n-1}=\prod_{j=1}^{\frac{m-1}{2} }\prod_{k=1}^{\frac{n-1}{2}} 　\left( 　4\cos^2\frac{2\pi j}{m}+4\cos^2\frac{2\pi k}{n} 　\right)}$

　ルジャンドル記号の式とこの式を見比べてみると、カッコ内の符号が逆になっているほかはまったく同じ形になっていることがわかりますね!
　これがただの偶然ではないというのです。

　J.Koizumi (sub)@J_Koizumi_233 さんのポストを元に少し解説します。

　奇素数 $p,q$ に対し、$(p-1)\times (q-1)$ のドミノタイリング $D$ を考え、垂直ドミノと水平ドミノの個数を別々にカウントします。すると水平なドミノの個数 $h(D)$ は必ず偶数になります。そこでDに $(-1)^{h(D)/2}$ というスコアを割り当てることにします。
　このとき、全てのドミノタイリングにわたるスコアの合計が $\left(\frac{q}{p}\right)$ にぴったり一致しているのです！

　さらに、$p,q$ が素数でない場合についても研究されているということで、J.Koizumi (sub)@J_Koizumi_233 さんのポストを引用します。

彼はまだ学部生ですが数学的才能に溢れており、今回もこの問題について相談した日の夜に完全な証明が送られてきて、大変驚かされました。一般の正整数m,nに対する(m-1)×(n-1)のドミノタイリングの場合は、mまたはnは奇数と仮定してよく、mが奇数である場合のスコアの合計は以下のようになります。 pic.twitter.com/7uuBncg7Vr
— J.Koizumi (sub) (@J_Koizumi_233) November 23, 2023

${\displaystyle \sum_{D\in \mathrm{D}(m-1,n-1)} (-1)^{\frac{h(D)}{2}} =\begin{cases} \left(\frac{n}{m}\right)&(n\equiv1\mod2)\\ \left(\frac{n/2}{m}\right)&(n\equiv0\mod2) \end{cases} }$

ここで左辺のD_(m-1,n-1)は(m-1)×(n-1)のドミノタイリング全体のなす集合です。右辺の(n/m)は平方剰余記号の拡張（Jacobi記号）であり、m=p_1×p_2×...と素因数分解して(n/p_i)を掛け合わせることで定義されます。
ちなみに、平方剰余の相互律（下式）は長方形の縦横を入れ替えることに対応しています。 pic.twitter.com/uKRem45f3k
— J.Koizumi (sub) (@J_Koizumi_233) November 23, 2023

${\displaystyle \left(\frac{n}{m}\right) =(-1)^{\frac{m-1}{2}\frac{n-1}{2}}\left(\frac{m}{n}\right) }$

　ということで、$m$ を奇数としたとき、スコアの総和はルジャンドル記号を一般化したヤコビ記号の値と一致することがわかったというのです!

ヤコビ記号についてはここをクリック / タップ

　ヤコビ記号(Jacobi記号)というのは、ルジャンドル記号を一般化したものです。任意の整数 $a$ と任意の正の奇整数 $n$ に対して、ヤコビ記号 ${\displaystyle 　\left(\frac{a}{n}\right) }$ は $n$ の素因数に対応するルジャンドル記号の積として定義されます。

${\displaystyle 　\left(\frac{a}{n}\right) =\left(\frac{a}{p_1}\right)^{\alpha_1} \left(\frac{a}{p_2}\right)^{\alpha_2} \cdots \left(\frac{a}{p_k}\right)^{\alpha_k} }$

ここで

${\displaystyle 　n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k} }$

は $n$ の素因数分解です。

下の引数が奇素数である場合、ヤコビ記号はルジャンドル記号と同じになります。

　私はこの論文の内容をまだほとんど理解していないので、語れることはあまりないのですが、それでも少し気が付いたことがあります。
　先のドミノタイリングの式を導出したときに、ドミノタイリングに対応するグラフの「タテの辺の重みを $i$ に、ヨコの辺の重みを $1$ に」して隣接行列を作るとパフィアンの絶対値がドミノタイリングの総数になったのですが、これを少しアレンジして、「タテの辺の重みを $1$ に、ヨコの辺の重みも $1$ に」してパフィアンを計算すると、 $(-1)^{h(D)/2}$ というスコアの総数になるはずです。

　そんなわけでパフィアンを計算するプログラムを作ろう……と思ったのですが、ググってもやり方がよくわからないので、chatGPT3.5と相談しながら作ることにしました。
　chatGPT3.5が作ってくれたパフィアン計算プログラムは、致命的なバグが複数あり、そのままでは使えませんでしたが、骨格部分はできていたので、半日くらいかけて修正したらちゃんとパフィアンが計算できるようになりました。
　とはいえ、もし私がchatGPTの力を借りなければ、今でもプログラムは完成していなかったことでしょう。今回、AIの恩恵・凄さというものを、最も感じた瞬間でした。

　……おっと、脱線しすぎましたね。話を元に戻しましょう。
　実際に計算した c++ のプログラムを以下に載せます。
　このプログラムは、 forループで $m,n$ を変化させて表を作ります。

        #include <bits/stdc++.h>
  #include <iostream>
  #include <vector>
  #include <algorithm>
  #include <complex>
  #include <numeric>
  #include <Eigen/Dense>
  
  using namespace std;
  using namespace Eigen;
  
  typedef long long ll;
  
  // 複素数型
  using Complex = complex<double>;
  
  // 複素行列型
  using ComplexMatrix = vector<vector<Complex>>;
  
  // ルジャンドル記号との関係を調べる
  // ドミノタイリングのときのグラフの辺の重みを全部1にする
  
  // 行列の中身を出力する関数
  void printMatrix(const ComplexMatrix& matrix) {
    for (const auto& row : matrix) {
        for (const auto& element : row) {
            cout << element << " ";
        }
        cout << endl;
    }
  }
  
  // 交代行列を取得する関数
  ComplexMatrix getSkewSymmetricMatrix(const ComplexMatrix& matrix) {
    ComplexMatrix skewSymmetricMatrix = matrix;
    for (int i = 0; i < matrix.size(); ++i) {
        for (int j = 0; j < matrix[i].size(); ++j) {
            skewSymmetricMatrix[i][j] = -matrix[j][i];
        }
    }
    return skewSymmetricMatrix;
  }
  
  // パフィアンの再帰的な計算
  Complex recursivePfaffian(const ComplexMatrix& matrix, const vector<int>& indices) {
    if (indices.size() == 2) {
        return matrix[indices[0]][indices[1]];
    }
  
    Complex result = 0.0;
    Complex s = Complex(1.0, 0);
  
    for (size_t i = 1; i < indices.size(); i ++) {
         if ( matrix[indices[0]][indices[i]] != 0.0){
            vector<int> subIndices(indices.begin(), indices.end());
            subIndices.erase(subIndices.begin() + 0);
            subIndices.erase(subIndices.begin() + i - 1);
            result += s * matrix[indices[0]][indices[i]] * recursivePfaffian(matrix, subIndices);
         }
         s = -s;
    }
        
  
    return result;
  }
  
  // パフィアンを計算
  Complex calculatePfaffian(const ComplexMatrix& matrix) {
    ComplexMatrix skewSymmetricMatrix = getSkewSymmetricMatrix(matrix);
  
    //cout << "Original Matrix:" << endl;
    //printMatrix(matrix);
  
    //cout << "\nSkew Symmetric Matrix:" << endl;
    //printMatrix(skewSymmetricMatrix);
  
    vector<int> indices(matrix.size());
    iota(indices.begin(), indices.end(), 0);
  
    return recursivePfaffian(skewSymmetricMatrix, indices);
  }
  
  int main() {
  
  // ドミノタイリングで水平ドミノの数をh(D)としたときのスコア(-1)^(h(D)/2)の総和
  //  by @apu_yokai
  
  // double の精度で計算しているため、頂点数が多くなると誤差がでてきます。
  
  for (int m = 2; m < 10; m += 2) {
    cout << "[" << m+1 << "]" ;
      for (int n = 1; n < 9; n++) {
  
        vector<pair<ll, ll>> V={};  // 頂点を入れる配列
      
        for(int jj = 1; jj <= n; jj++) {
            for (int ii = m; ii >= 1; ii--) {
              V.push_back(make_pair(m + 1 - ii, jj));
            }
        }
        
        // 行列式計算のための複素行列の宣言
        MatrixXcd complexMatrix(V.size(), V.size());
        
        // パフィアン計算のための行列の宣言(同じ行列を作っており冗長　要改善)
        ComplexMatrix copymatrix(V.size(),vector<Complex>(V.size()));
      
        for (int ii = 0; ii < V.size(); ii++) {
          for (int jj = 0; jj < V.size(); jj++) {
            int i = V.at(ii).first;
            int j = V.at(ii).second;
            int k = V.at(jj).first;
            int l = V.at(jj).second;
            
            // ここから隣接行列の成分を作成
            // parity が -1 のときは縦方向を -1倍にしている
            
            if ( k == i && l == j - 1) { complexMatrix(ii, jj) = complex<double>(-1.0, 0.0);
                                                       copymatrix[ii][jj]=complex<double>(-1.0, 0.0);}
            else if (k == i && l == j + 1) { complexMatrix(ii, jj) = complex<double>(1.0, 0.0);
                                                          copymatrix[ii][jj]=complex<double>(1.0, 0.0);}
            else if (k == i + 1 && l == j) { complexMatrix(ii, jj) = complex<double>(1.0, 0.0);
                                             copymatrix[ii][jj]=complex<double>(1.0, 0.0);}
            else if (k == i - 1 && l == j) { complexMatrix(ii, jj) = complex<double>(-1.0, 0.0);
                                             copymatrix[ii][jj]=complex<double>(-1.0, 0.0);}
            else  { complexMatrix(ii, jj) = complex<double>(0.0, 0.0);
                    copymatrix[ii][jj]=complex<double>(0.0, 0.0);
            }
          }
        }
        
          // 行列式を計算し、実部を取り出す(虚部はゼロになる)
          double det = complexMatrix.determinant().real();
        
          // パフィアンを計算し、実部を取り出す(虚部はゼロになる)
          Complex pf = calculatePfaffian(copymatrix);
        
          // 出力の精度を設定
          cout << setprecision(15); // 15桁の精度
        
          // 結果を出力
          //cout << "パフィアンの値(実部・虚部): " << pf << endl;
          //cout << "パフィアンの値(実部): " << pf.real() << endl;
          //cout << "行列式の値: " << det << endl;
          cout << pf.real() << " ";
      }
      cout << endl;
  }
  return 0;
  }

　このプログラム、出力しないのに行列式も計算しているのは、いろいろ実験して遊ぶことを想定しているからです。
　行列式計算部分を削除すればもっと短く、軽くすることもできますのでいろいろアレンジしてもらえればと思います。
　それを含めてかなり冗長な処理になってしまっていると思いますが、素人がchatGPT3.5と相談しながら作ったプログラムということで大目に見ていただければと思います。

アルゴリズム

　パフィアンを計算するアルゴリズムを簡単に説明します。
　計算には、パフィアンの次の性質を使っています。

　 $A$ を任意の $2n\times 2n$ 交代行列とする。 $A$ から $i,j$ 行と $i,j$ 列を除去して得られる行列を $A^{ij}$ と表すとき

　${\displaystyle \operatorname{Pf}A = \sum_{j=2}^{2n}(-1)^ja_{1j}\operatorname{Pf}A^{1j}}$

　これは行列式における余因子展開にあたる公式で、これを再帰的に適用することでパフィアンを求めることができるというわけです。
　なお、$a_{1j}$ がゼロのときは計算を打ち切ることで高速化しています。

出力結果

　さておき、出力結果はつぎのようになりました。
[ ]は $m=3,5,7,9$ を表しています。
各行は左から $n=2,3,\cdots,9$ を表しています。

      [3]1 0 -1 -1 0 1 1 0 
[5]1 -1 -1 0 -1 -1 1 1 
[7]1 -1 1 -1 -1 0 1 1 
[9]1 0 1 1 0 1 1 0

この表が Wikipedia のヤコビ記号の表と一致するのかどうか見比べてみると・・・

(Wikipedia のヤコビ記号の表をもとに作成)

$m$	$\left(\frac{2}{m}\right)$	$\left(\frac{3}{m}\right)$	$\left(\frac{4}{m}\right)$	$\left(\frac{5}{m}\right)$	$\left(\frac{6}{m}\right)$	$\left(\frac{7}{m}\right)$	$\left(\frac{8}{m}\right)$	$\left(\frac{9}{m}\right)$
3	-1	0	1	-1	0	1	-1	0
5	-1	-1	1	0	1	-1	-1	1
7	1	-1	1	-1	-1	0	1	1
9	1	0	1	1	0	1	1	0

　……あれ?少し違いますね?
　……と思って見直してみると

${\displaystyle \sum_{D\in \mathrm{D}(m-1,n-1)} (-1)^{\frac{h(D)}{2}} =\begin{cases} \left(\frac{n}{m}\right)&(n\equiv1\mod2)\\ \left(\frac{n/2}{m}\right)&(n\equiv0\mod2) \end{cases} }$

　ですから、
「$n$ が奇数のときはヤコビ記号の表の $n$ 列目と一致し、
$n$ が偶数のときはヤコビ記号の表の $n/2$ 列目と一致する」
ということでした。
　少しややこしいですが、これにあわせて表をこんな風に修正してみると……

$m$	$\left(\frac{2/2}{m}\right)$	$\left(\frac{3}{m}\right)$	$\left(\frac{4/2}{m}\right)$	$\left(\frac{5}{m}\right)$	$\left(\frac{6/2}{m}\right)$	$\left(\frac{7}{m}\right)$	$\left(\frac{8/2}{m}\right)$	$\left(\frac{9}{m}\right)$
3	1	0	-1	-1	0	1	1	0
5	1	-1	-1	0	-1	-1	1	1
7	1	-1	1	-1	-1	0	1	1
9	1	0	1	1	0	1	1	0

プログラムが出力した表と確かに一致していることが確認できました!

ドミノタイリングパズルで未解決問題が生えた話

　さて、時が少し戻って $10$ 月 $27$ 日。私が任意のポリオミノをドミノで埋め尽くす総数を計算するアルゴリズムを考えていることをX(Twitter)でつぶやいていると、Tatt（たっと）(@tatt61880) さんがこんなゲームを作ってくれました。

ブラウザ上で動作するようにしてみました！
現時点では、幅と高さを6に固定しています。

“ドミノ数え上げ” https://t.co/cQHPWsBW70 pic.twitter.com/0OqGFtzjvw
— Tatt（たっと） (@tatt61880) October 27, 2023

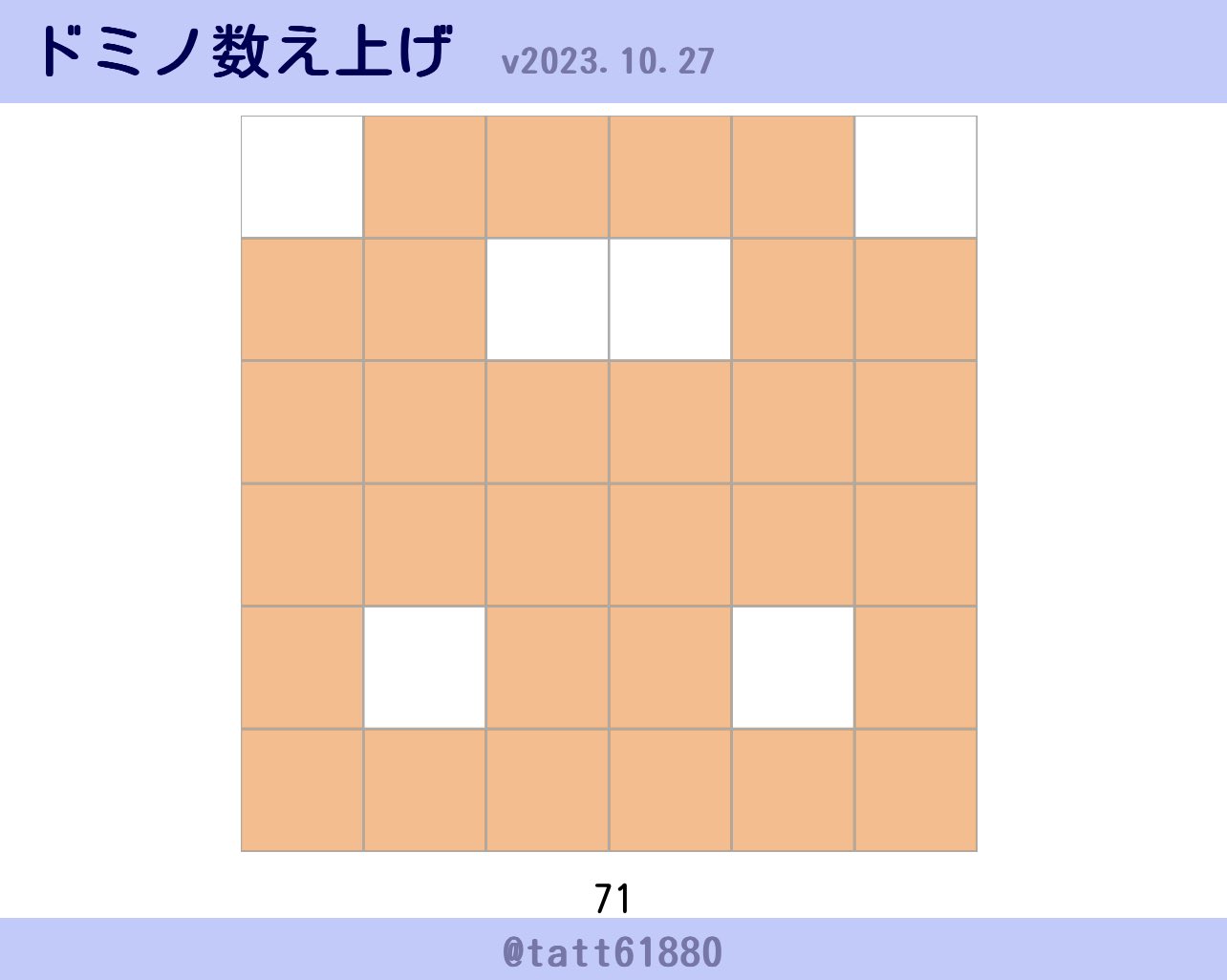ドミノ数え上げゲーム

　自由にタイルを配置して、すぐにドミノ配置パターンが何通りあるかわかり、しかも、見つけたパターン数をコレクションできる楽しいゲームです。
　遊んでいると時間が溶けてしまう危険なゲームです。

　ここから、意外な方向へ話が転がっていきます。
　このドミノ数え上げゲームでステージの大きさを無限にしたら全ての自然数のパターンを網羅できるかどうかについてポストしたところ……

apu_yokaiの11月18日のポスト
X(旧Twitter)apu_yokai:ドミノ数え上げゲーム、ステージの大きさを無限にしたら全ての自然数のパターンを網羅できるだろうか？

　このポストのリプライにあるように、suisen(@_su1sen)さん、べーたTCM-β(@tcmbeta)さん、
Tatt（たっと）(@tatt61880) さんが任意の自然数とおりを構成できるパターンを色々と構成してみせてくれました。
　つまり、ステージの広さが無限であれば、任意の数のパターンが構成可能なのです!

　自分で考えたい人もいると思いますので、具体的な構成例は↓に隠しておきます。

任意の自然数とおりを構成できるパターンの例についてはここをクリック / タップ

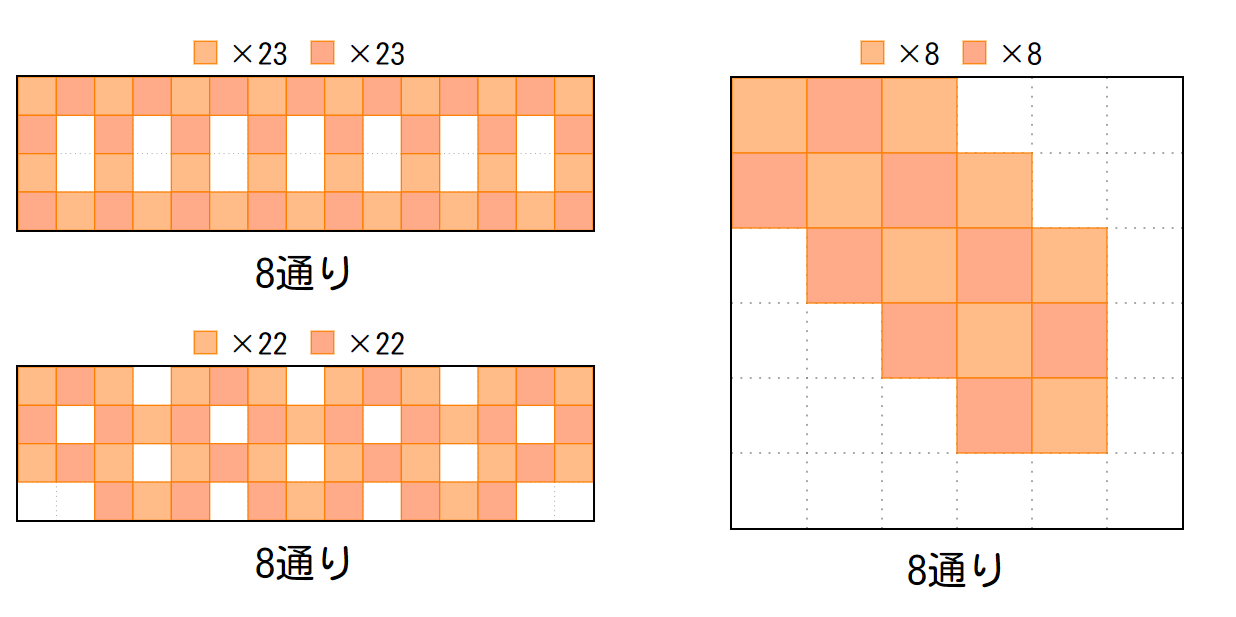任意の自然数とおりを構成できるパターンの一部

　というわけで、↑のパターンを見れば、「高さ $4$ 以上、幅無制限」の条件であれば任意の自然数のパターンを構成することが可能であることがわかります。

　次に、「高さ $3$ 、幅無制限」の条件について考えます。
　さすがに、高さ $3$ では無理だろう、……と思っていたのですが。

べーたTCM-β@tcmbeta さんの11月30日のポスト
X(旧Twitter)tcmbeta:手計算を諦め、プログラムにより4桁の素数は全部可能と判明しました。大きな素数でも、例えば100003を構成することができました↓

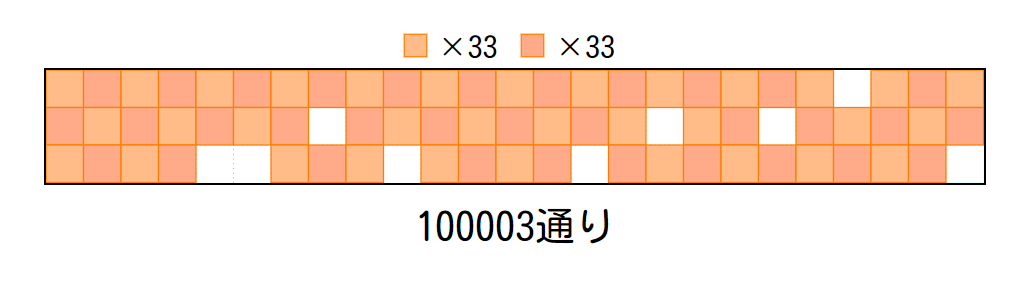100003とおりのパターン

　なんと、少なくとも $4$ 桁以下の素数ですべて可能と判明。合成数の場合は、素数の場合のパターンを組み合わせることで構成できますので、結局 $4$ 桁以下のすべてのパターンが可能だというのです。こうなってくると、全ての自然数で可能である可能性が出てきました。
　この記事を書いている $2023$ 年 $12$ 月 $9$ 日現在、この問題は未解決のままです。もし、「反例が見つかった!」とか、「可能であることが証明できた!」という情報があれば教えていただきたいと思います。

おわりに

　というわけで、$2023$ 年後半にいろいろな方向へ発展をみせたドミノタイリングの話題を総括してみました。
　私は普段、こんな感じでX(旧Twitter)上で情報交換しながら日曜数学活動をしています。一人ではたどりつけない世界でも、みんなで議論しながらなら垣間見ることができるのがこのスタイルのいいところですね。
　
　これでこの記事はおしまいですが、ドミノタイリングにはまだまだ面白い話題がかくれていそうです。
　みなさんもドミノタイリングで遊んでみてください!

　それでは明日のアドベントカレンダーは kiguro_masanao さんの「書籍『笑わない数学』裏話」ですね!
　それでは～。