第1章(後半)

⑦ジュルゴンヌ点(X(7))とナーゲル点(X(8))

赤い点がジュルゴンヌ点である。[15]

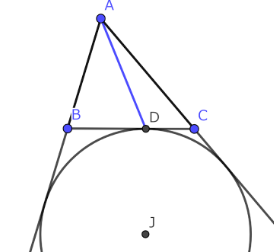青い線がsplitterである。

[16]　

赤い点がナーゲル点[15]

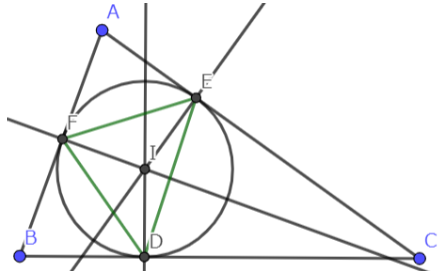緑の三角形が内接三角形である。

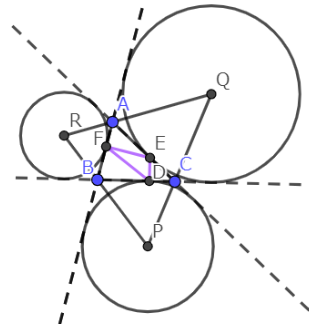紫の三角形が傍接三角形である。

私は初めは簡潔な証明が思いつかなかった。[17]を見て証明方法が分かった。

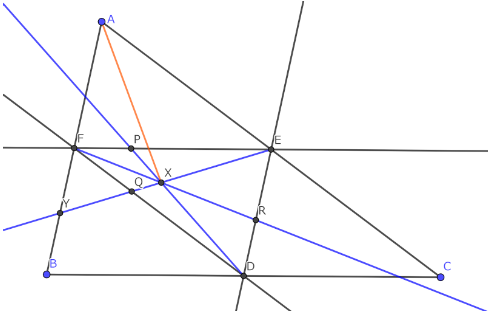中点三角形のナーゲル点Xが角の二等分線(橙)の交点になる。

⑧シュピーカー点

赤い点がシュピーカー点である。[18]

シュピーカー点には面白い性質がいくつかあるが、三角形の中心の勉強を進めないと、面白さをすぐには実感できない。ここには載せないが具体例としては、
①三角形における「面の重心」「頂点の重心」が、重心であるのに対し、「辺の重心」がシュピーカー点である。
簡単に言うと、重さが無視できる三角形の板の周囲に、十分に重さがあり太さが無視できる枠組みをとりつける。板のある点から糸で吊したときに板が水平になるとき、その点は
シュピーカー点である。
②3本のクリバー線(辺の中点を通り三角形の周を二等分する線）の交点である。
③垂心、mittenpunkt、シュピーカー点は同一直線上である。
④テイラー点(六点円、すなわち垂足三角形の各頂点から元の三角形の各辺に下した垂足6つを通る円の中心)は、垂足三角形のシュピーカー点である。
⑤excircles radical circle(3つの傍接円に直交する円)の中心はシュピーカー点である。
⑥キーペルト双曲線上である。
⑦シュピーカー円はナーゲル点と各頂点の中点を結ぶ三角形の内接円である。
などが挙げられる。

⑨ナーゲル線
証明は三線座標やベクトルを用いることが多いが、煩雑！
しかし重心の特性定理を用いることで、簡単に示せる。

ナーゲル線を表す。[19]

⑩ド・ロンシャン点

赤い点がド・ロンシャン点である。[20]

定義から明らかに、ドロンシャン点はオイラー線上である。

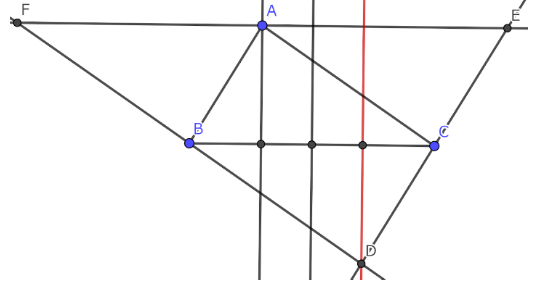赤い直線が逆垂線

各辺に垂直な直線と三角形の中心が対応している。[21]

★中点三角形と元の三角形との対応関係

ウィキペディアの情報をもとに作成。[22]

この表に掲載されている情報は全て証明済みである。

参考文献
これらの情報は全て2024年5月26日時点での情報である。
[1]  『外接円の半径と三角形の面積の関係』 https://manabitimes.jp/math/577
[2]  『ヘロンの公式の証明と使用例』  https://manabitimes.jp/math/579
[3]　『三角形の外接円の半径、内接円の半径と面積の関係S=1/2r(a+b+c)』
https://examist.jp/mathematics/trigonometric-ratio/gaisetuen-naisetuen-hankei/#google_vignette
[4]『三角形の五心の覚えておくべき性質を整理』 https://manabitimes.jp/math/628
[5]『三角形の重心・外心・垂心の位置関係(オイラー線)の幾何的証明』 https://examist.jp/mathematics/plane-figure/euler-line-syoumei/
[6]『九点円の定理の証明と諸性質』 https://manabitimes.jp/math/690
[7]『Euler Line』 https://mathworld.wolfram.com/EulerLine.html
[8]『九点円の中心がオイラー線上にあることの初等的な証明』 https://mathlog.info/articles/3336
[9]『フォイエルバッハ(Feuerbach)の定理』 http://yosshy.sansu.org/theorem/feuerbach.htm
[10]『Tangent Circles』 https://mathworld.wolfram.com/TangentCircles.html
[11]『Apollonius circle』 https://mathworld.wolfram.com/ApolloniusCircle.html
[12]『シムソン線であそぼう！』 https://mathlog.info/articles/3778
[13]『垂足三角形』 https://kikagaku.at-ninja.jp/triangle_geometry/orthic_triangle.html
[14]『Orthic Triangle』 https://mathworld.wolfram.com/OrthicTriangle.html
[15]『ジュルゴンヌ点とナーゲル点の存在証明』 https://manabitimes.jp/math/912
[16]『傍心の意味と性質・内心との比較』 https://manabitimes.jp/math/633
[17]『Why is the Incenter the Nagel Point of the Medial Triangle?』 https://polymathematics.typepad.com/polymath/why-is-the-incenter-the-nagel-point-of-the-medial-triangle.html
[18]『シュピーカー点』 https://ja.wikipedia.org/wiki/%E3%82%B7%E3%83%A5%E3%83%94%E3%83%BC%E3%82%AB%E3%83%BC%E7%82%B9
[19]『Nagel Line』 https://mathworld.wolfram.com/NagelLine.html
[20]『ド・ロンシャン点』 https://ja.wikipedia.org/wiki/%E3%83%89%E3%83%BB%E3%83%AD%E3%83%B3%E3%82%B7%E3%83%A3%E3%83%B3%E7%82%B9
[21]『de Longchamps point』 https://en.wikipedia.org/wiki/De_Longchamps_point
[22]『中点三角形』 https://ja.wikipedia.org/wiki/%E4%B8%AD%E7%82%B9%E4%B8%89%E8%A7%92%E5%BD%A2#:~:text=%E4%B8%AD%E7%82%B9%E4%B8%89%E8%A7%92%E5%BD%A2%EF%BC%88%E3%81%A1%E3%82%85%E3%81%86%E3%81%A6%E3%82%93,%E3%81%A8%E3%81%99%E3%82%8B%E4%B8%89%E8%A7%92%E5%BD%A2%E3%81%A7%E3%81%82%E3%82%8B%E3%80%82
[23]『中線定理とスチュワートの定理』
https://gleamath.com/parallelogram-and-stewarts-thm/
[24]『Bevan Point』 https://mathworld.wolfram.com/BevanPoint.html
[25]『五心間の距離等』 https://masagon7.jimdo.com/6-%E4%BA%94%E5%BF%83%E9%96%93%E3%81%AE%E8%B7%9D%E9%9B%A2/
[26]『オイラーの定理（内心と外心の距離）とオイラーの不等式の証明を3通りずつ』 https://manabitimes.jp/math/580
[27]『Fuhrmann Circle』 https://mathworld.wolfram.com/FuhrmannCircle.html
[28]『ETC』 https://faculty.evansville.edu/ck6/encyclopedia/ETC.html
[29]『等角共役点の証明』 https://su-hai.hatenablog.com/entry/6569200
[30]『等角共役線』 https://kikagaku.at-ninja.jp/triangle_geometry/isogonal_conjugate_lines.html
[31]『逆平行』 https://kikagaku.at-ninja.jp/triangle_geometry/antiparallel.html
[32]『Symmedianまとめ(類似中線)』 https://mathlog.info/articles/3400
[33]『Lemoine点(類似重心)』 https://kikagaku.at-ninja.jp/triangle_geometry/Lemoine_point.html
[34]『Gergonne点』 https://kikagaku.at-ninja.jp/triangle_geometry/Gergonne_point.html
[35]『等角共役点』 https://kikagaku.at-ninja.jp/triangle_geometry/isogonal_conjugate_points.html
[36]『Mandart Circle』 https://mathworld.wolfram.com/MandartCircle.html
[37]『ONE LINE PROOF OF LEMOINE'S PEDAL TRIANGLE THEOREM』
https://www.researchgate.net/publication/312653562_ONE_LINE_PROOF_OF_LEMOINE%27S_PEDAL_TRIANGLE_THEOREM#:~:text=Lemoine%27s%20theorem%20states%20that%20the,72
[38]『Lemoine円』 https://kikagaku.at-ninja.jp/triangle_geometry/Lemoine_circles.html
[39]『デカルトの円定理と2通りの証明』 https://manabitimes.jp/math/2867
[40]『デカルトの円定理』 https://ja.wikipedia.org/wiki/%E3%83%87%E3%82%AB%E3%83%AB%E3%83%88%E3%81%AE%E5%86%86%E5%AE%9A%E7%90%86
[41]『Soddy Circles』 https://mathworld.wolfram.com/SoddyCircles.html
[42]『三頂点からの距離の和、二乗の和が等しい点』 https://masagon7.jimdo.com/8-%E4%B8%89%E8%BE%BA%E3%81%AE%E5%92%8C-%E4%BA%8C%E4%B9%97%E3%81%AE%E5%92%8C%E3%81%8C%E7%AD%89%E3%81%97%E3%81%84%E7%82%B9/
[43]『垂足三角形と相似な三角形』 https://gleamath.com/pedal-triangle-and-similar-triangles01/
[44]『Adams’ Circles』 https://mathworld.wolfram.com/AdamsCircle.html
[45]『perspector』 https://mathworld.wolfram.com/Perspector.html