連載 グラフアートを描こう 第5回 グラフを回そう 前編 掛け算って何?

この記事に含まれる全ての画像は自作です。

注意事項

この記事は特定の国家や思想を批判するものではありません。

イントロダクション

この記事は、「連載 グラフアートを描こう」の第5回です。
第1回 、 第2回 、 第3回 、 第4回 を読んでいない人はそちらから読んでいただくとより理解が深まります。

本編

数直線

突然ですが、掛け算について考えましょう。

掛け算は、「原点が同じで基準の長さ($ 0 $から$ 1 $までの距離)が異なる2本の数直線」によって可視化することができます。例えば、この図を見てください:

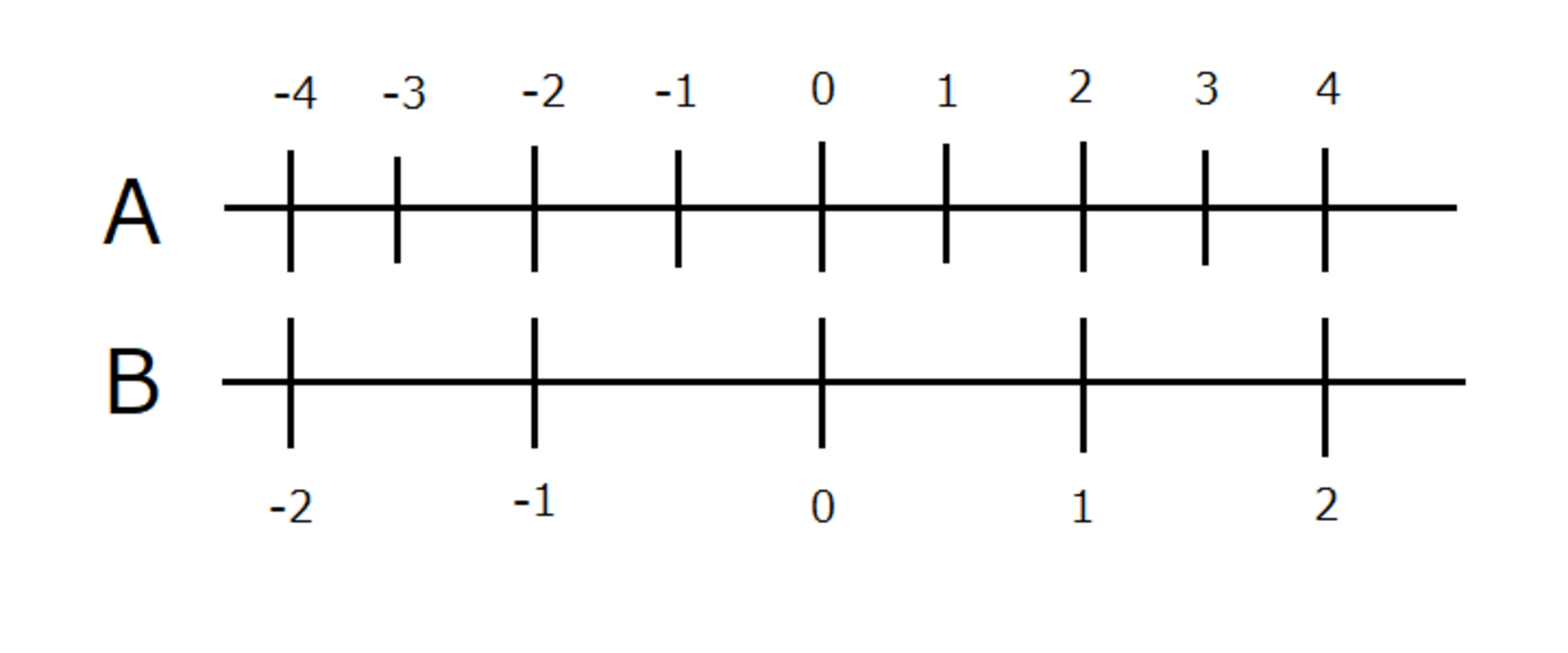原点が同じで基準の長さが異なる2本の数直線

Aの数直線の$ 2 $が、Bの数直線の$ 1 $に対応しています。

ここで、AB両方に目盛りがあるところの値を取り出してみましょう。

AはBの$ 2 $倍になっていますね。つまり、これらの数直線は、掛け算の表として使えるということです。別の例を見てみましょう。

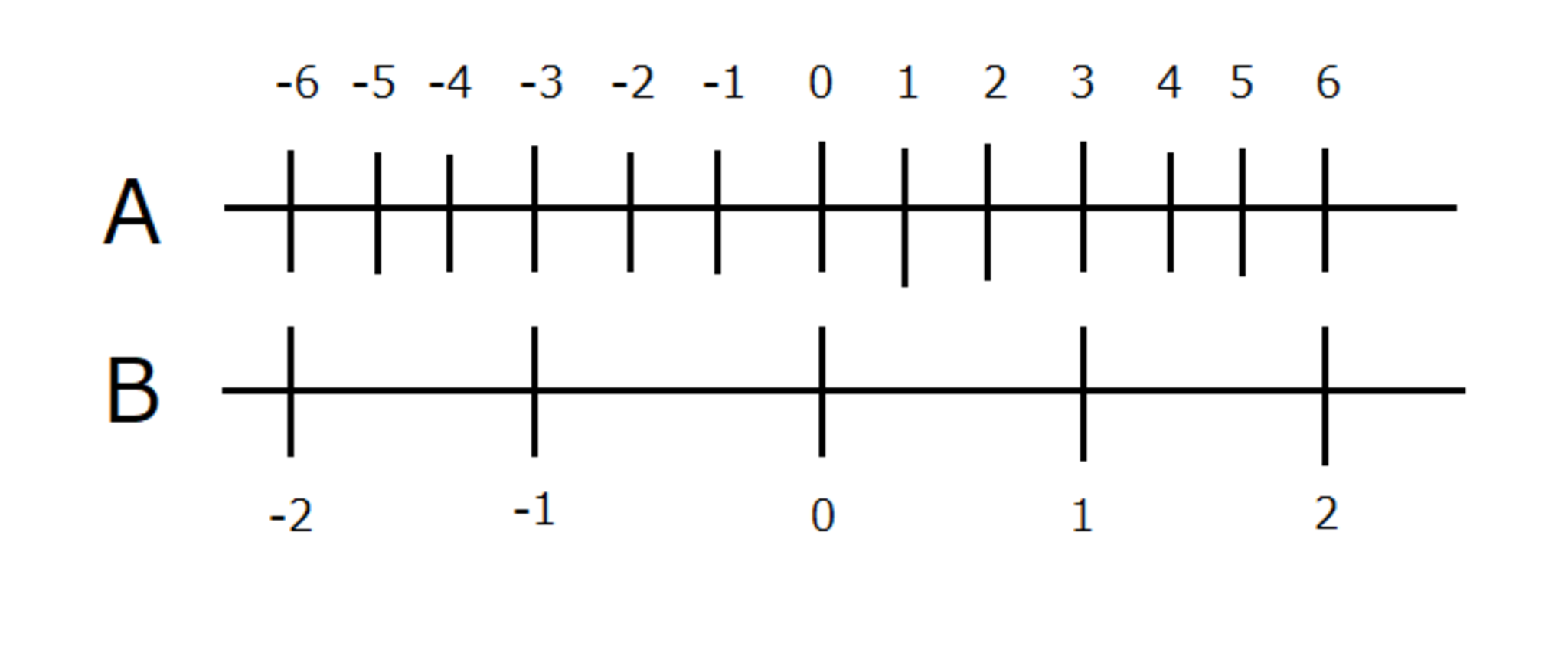原点が同じで基準の長さが異なる2本の数直線

この例では、AはBの$ 3 $倍になっています。では、この赤い線に注目してみましょう。

$\text{A}の\hspace{1mm}6\hspace{1mm}が\text{B}の\hspace{1mm}2\hspace{1mm}に対応する$

Bの$ 2 $にAの$ 6 $が対応しています。AはBの$ 3 $倍なので、この図は

$$ 3 \times 2 = 6 $$

を表していることになります。($ 2 \times 3 = 6 $でもいいのですが、一貫性を持たせるためにこの記事では倍率を左に書くことにします)

もちろん、整数だけではありません。こんなふうにBの$ 0 $と$ 1 $の間に線を引くと、

$\text{A}の\hspace{1mm}\frac{3}{2}\hspace{1mm}が\text{B}の\hspace{1mm}\frac{1}{2}\hspace{1mm}に対応する$

$$ 3 \times \frac{1}{2} = \frac{3}{2} $$

という分数の計算もできます。

小数を使った例を見てみましょう。

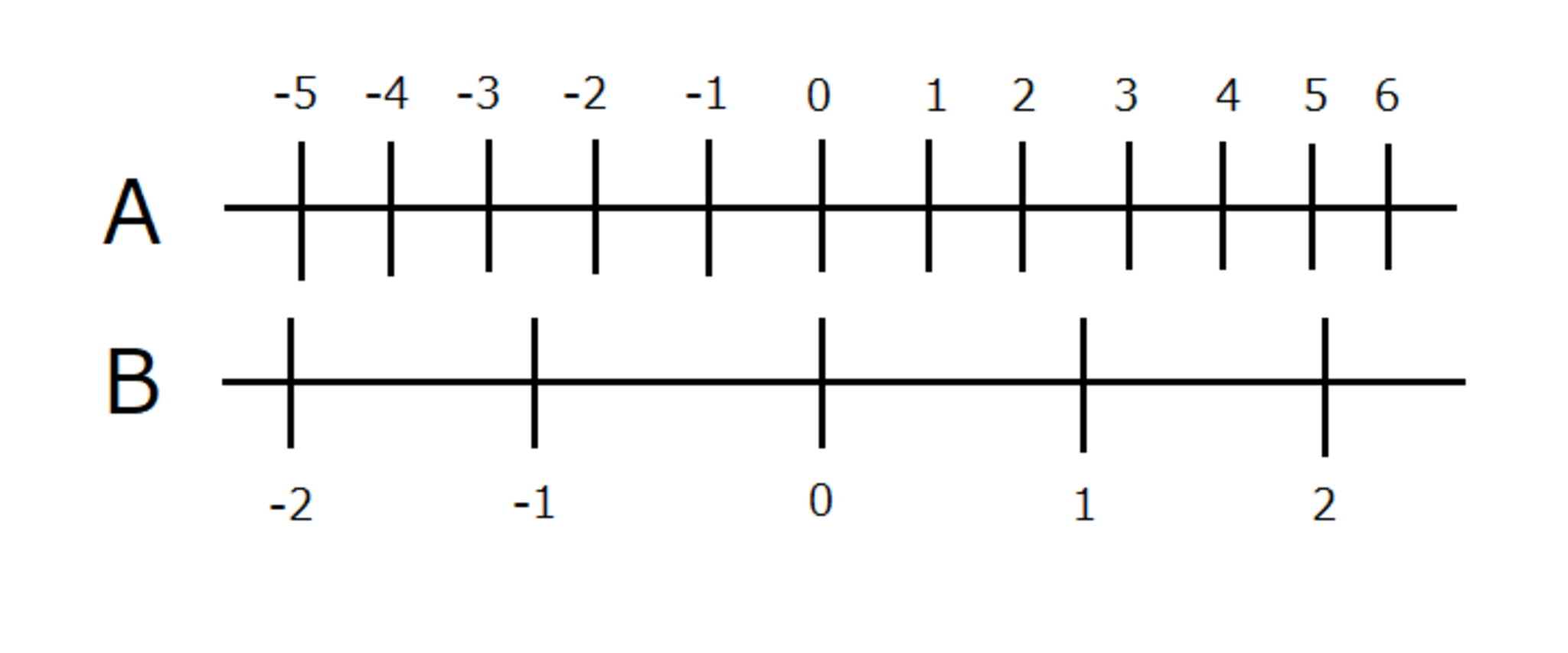別の一対の数直線

この図では、Bの$ 1 $はAの$ 2.54 $に対応しています。これを使って、$ 2.54 \times 1.25 $の近似値を読み取ってみましょう。

$2.54 \times 1.25\hspace{1mm}を表した図$

Bの$ 1.25 $の位置には、Aの$ 3.2 $くらいに対応していることがわかりますね。すなわち、

$$ 2.54 \times 1.25 \approx 3.2 $$

であることがわかります。実際の値は

$$ 2.54 \times 1.25 = 3.175 $$

なので、確かに掛け算を計算できていることが分かります。

負の数の掛け算

この考え方は、負の数にも適用することができます。

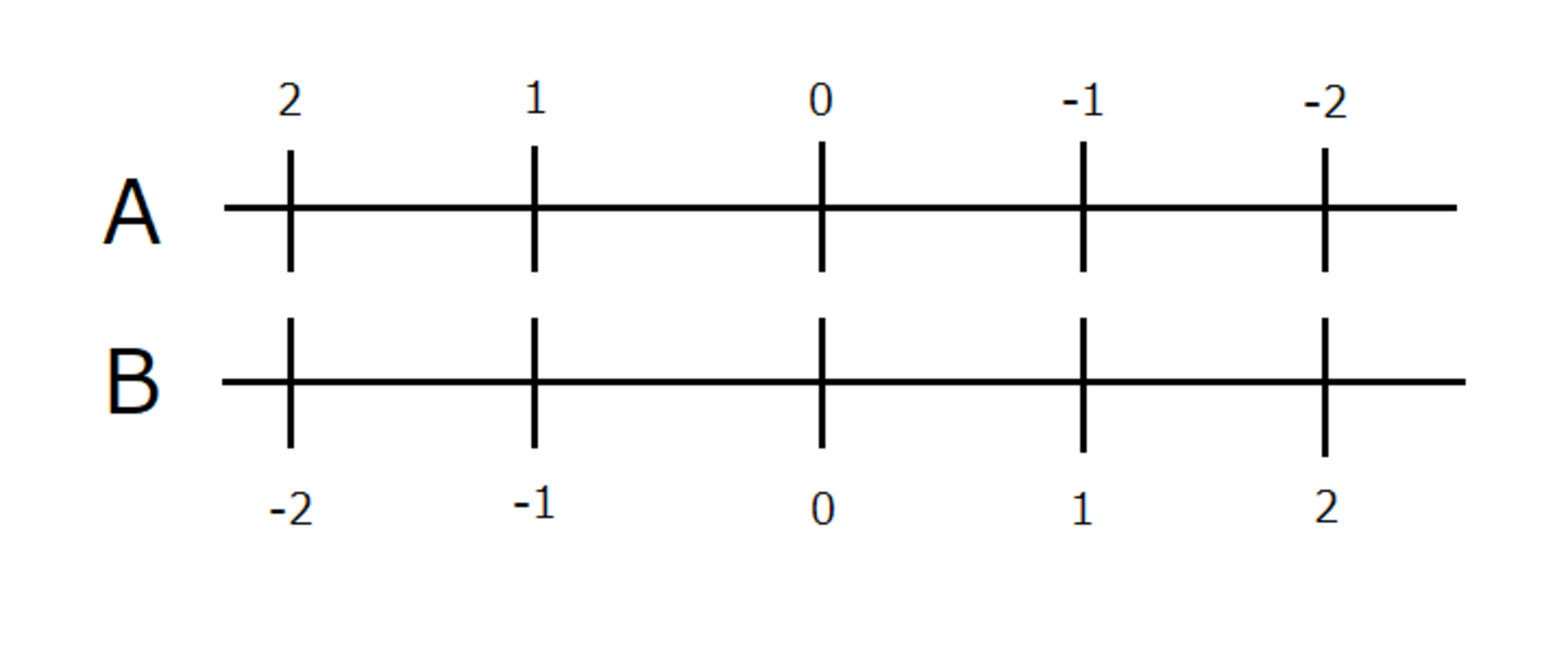互いに逆向きの数直線

AとBは、$ 0 $から$ 1 $までの長さは同じですが、左右が逆になっています。
Bの$ 1 $の上には、Aの$ -1 $がありますね。

これは、$ -1 $倍を表していると言えます。実際、上の図では

$$ -1 \times (-2) = 2,\hspace{5mm} -1 \times (-1) = 1,\hspace{5mm} -1 \times 0 = 0,\hspace{5mm} -1 \times 1 = -1,\hspace{5mm} -1 \times 2 = -2 $$

が成り立っています。

もちろん、反転してかつ基準の長さが異なるということもあり得ます。

$-2\hspace{1mm}倍を表す数直線$

この図では、AはBの$ -2 $倍になっています。$ -2 \times (-1) = 2 $や$ -2 \times 2 = 4 $を確認することができますね。

次回予告

なんでこんなことをやったのかは、次回わかります。
第6回 は、「グラフを回そう 中編 複素数」です。