高校数学解説

連載グラフアートを描こう第6回グラフを回そう中編複素数

グラフアート,オイラーの公式,複素数

366

この記事に含まれる全ての画像は自作です。

イントロダクション

この記事は、「連載グラフアートを描こう」の第6回です。
第1回、第2回、第3回、第4回、第5回を読んでいない人はそちらから読んでいただくとより理解が深まります。

本編

では早速ですが、$ 2 $乗して$ -1 $になる数、すなわち$ x \times x = -1 $を満たす$ x $について考えましょう。

前回の方法で考えると、「Bの$ 1 $がAの$ x $に対応するとき、Bの$ x $がAの$ -1 $に対応する」ような$ x $を求めればよいですね。

そのような$ x $は、どこにあるでしょうか。

実数の$ 2 $乗は必ず$ 0 $か正ですから、数直線の中にはありません。

その数は、$ 0 $から$ 1 $だけ上に行った場所にあります。

!FORMULA[14][1319579607][0] $2\hspace{1mm}乗して\hspace{1mm}-1\hspace{1mm}になる数$

Aを黒、Bを赤で示しています。たしかに、Bの$ 1 $がAの$ x $に対応し、Bの$ x $がAの$ -1 $に対応していることが分かりますね。

「そんなのありかよ！」と思うかもしれませんが、これが数学です。

この$ x $は虚数単位と呼ばれ、一般に$ i $という記号で表されます。工学系の文献では電流と文字が被るのを避けて例外的に$ j $を使うことが多いようですが、この記事では$ i $を用いることにします。

複素数

では、数直線を$ i $も含めた世界に拡張してみましょう。

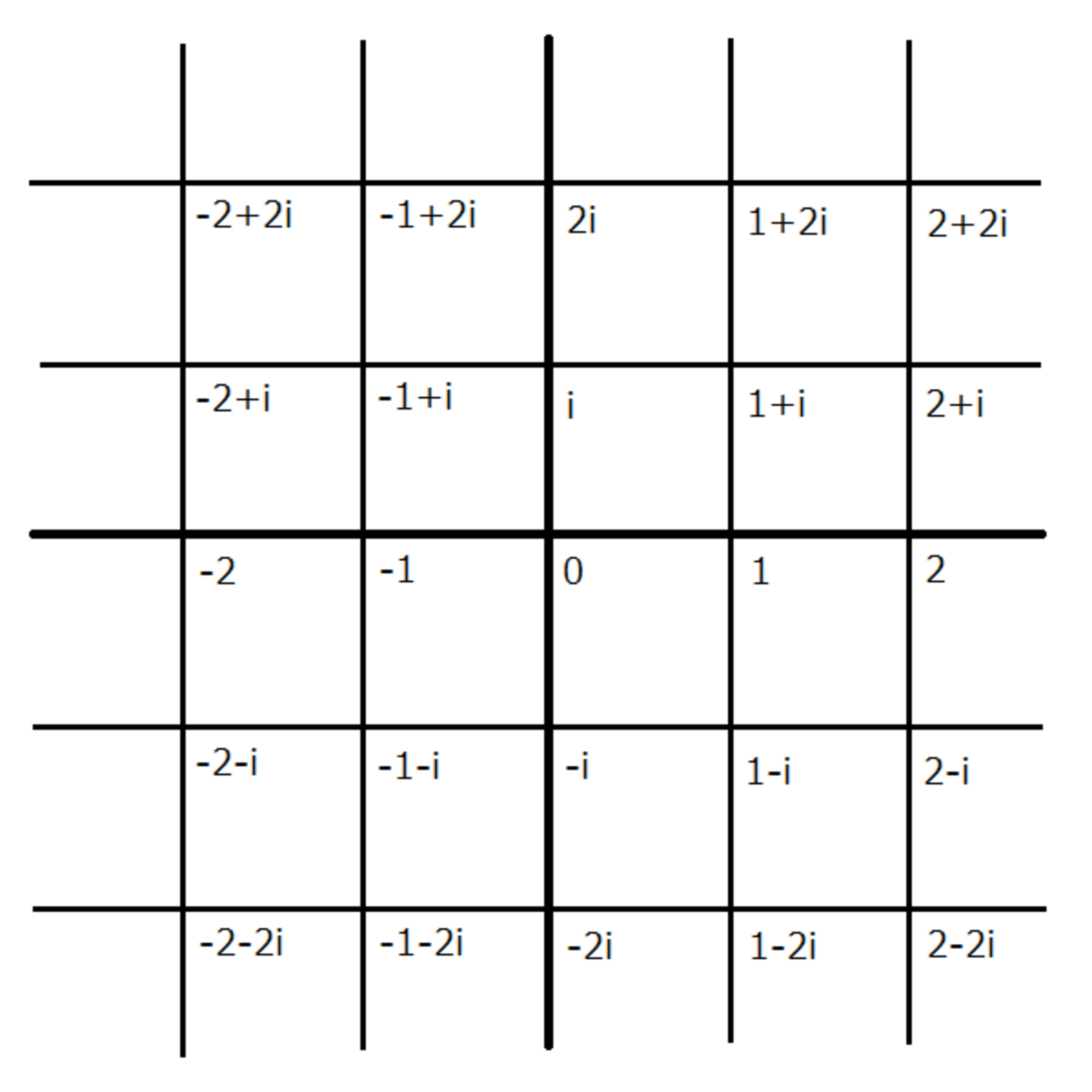複素平面

この碁盤の目に広がった世界全体に数が分布しています。こうして広がった世界にある数のことを、複素数といいます。$ 1 $や$ i $もこの世界の一部なので複素数に含まれます。

$ 1 + 2\sqrt{2} $などがこれ以上簡単にできないように、$ 1 + 2i $などもこれ以上簡単にできないことに注意してください。

また、$ 1 + 2\sqrt{2} $などと同じように、複素数も「実数部分、$ i $の係数、$ i $」の順序で書くことが多いです。

この世界での計算は、$ i^2 = -1 $に注意すれば、文字式の計算と同様にできます。

複素数の計算の例

$$ (1 + 2i) + (3 - 4i) = 4 - 2i $$

$$ (1 + 2i) (3 - 4i) = 3 + 2i - 8i^2 = (3 + 8) + 2i = 11 + 2i $$

一般に、$ a, b, c, d $を実数として

$$ (a + bi) + (c + di) = (a + c) + (b + d)i $$

$$ (a + bi)(c + di) = ac + (ad + bc)i + bdi^2 = (ac - bd) + (ad + bc)i $$

回転を表す複素数

突然ですが、$ z = \cos{72^\circ} + i\sin{72^\circ}$とおいて、複素数にこの$ z $を掛けるとどうなるか見てみましょう。

前回の考え方を使って考えてみましょう。

$ \cos^2{72^\circ} + \sin^2{72^\circ} = 1 $ですから、$ 1 $が$ z $の位置まで回転することになります。

!FORMULA[42][-659245401][0]

$座標軸が\hspace{1mm}72\hspace{1mm}度回転する$

すなわち、この$ z $は、反時計回りに$ 72 $度回転させる操作を表していると言えます。

一般に、$ w = \cos{\alpha} + i\sin{\alpha} $は、反時計回りに$ \alpha $回転させる操作を表していると言えます。