【Causality】全悪質時空１
因果的な性質としては最悪の性質を持つ全悪質時空の因果構造について解説します。全悪質時空はその因果的性質の悪質さからあまり多くの研究がなされていません。しかし私は以下の理由から割と面白い対象だと思っています。
- Godel宇宙など相対論で有名な例がある
- コンパクト時空を考える時、ほぼ必然的に全悪質かどうかという問題意識を持つことができる
- 与えられた時空が全悪質かどうかを完全に判定することは難しい。
- 時空という描像で時間と空間を捉えようとするとき、結局時間とは何なのかという形而上学的な疑問をもたらす
この記事の内容の9割は
Matori, Totally vicious space‐times and reflectivity (1987)
https://aip.scitation.org/doi/10.1063/1.527977
の解説です。
全悪質は英語ではTotally Viciousと言います。全悪質はあまり一般的な用語ではありませんので、この記事では以降、Totally ViciousまたはTV時空と書くことにします。
Totally Vicious時空の定義
まずは定義からですが、同値な定義がいくつかあります。
時空$(M,g)$がTotally Viciousであるとは次の同値な条件のいずれかを満たすことである。
(T1) 任意の$p\in M$に対して、$ I^+(p)\cap I^-(p)=M$
(T2) ある$p_0\in M$に対して、$ I^+(p_0)\cap I^-(p_0)=M$
(T3) 任意の$p\in M$に対して、$p$を通る閉timelike曲線(CTC)が少なくとも一つ存在する。
(T4) 任意の$p,q\in M (p\ne q)$に対して、$p$と$q$を結ぶtimelike曲線が少なくとも一つ存在する。
(V1) 任意の$p\in M$に対して、$ J^+(p)\cap J^-(p)=M$
(V2) ある$p_0\in M$に対して、$ J^+(p_0)\cap J^-(p_0)=M$
まずはこれらの条件が同値であることを証明しましょう。
(T1)$\Rightarrow$(T2)
自明
(T2)$\Rightarrow$(T1)
任意の$p,q\in M$に対して、$ I^+(p_0)\cap I^-(p_0)=M$であるから、$p_0<< p<< p_0<< q<< p_0$となる。よって$p<< q<< p$となり、$q\in I^+(p)\cap I^-(p)$となる。従って$M\subset I^+(p)\cap I^-(p)$である。
(T1)$\Rightarrow$(T3)
自明
(T3)$\Rightarrow$(T2)
次の簡単な補題が成り立つことが分かる。
補題：$II(p):=I^+(p)\cap I^-(p)$と書くとき、$II(p)\ne\emptyset,II(q)\ne\emptyset$が$II(p)\cap II(q)\ne\emptyset$ならば、$II(p)=II(q)$である。
この補題を使うと次のように証明できる。$p\in I^+(p)\cap I^-(p)$であるから、$ M=\bigcup_{p\in M}\{I^+(p)\cap I^-(p)\}$である。補題より$ M$は$ I^+(p)\cap I^-(p)$の形をした集合のdisjoint unionであり、Mは連結で$ I^+(p)\cap I^-(p)$はopenなので$ M=I^+(p_0)\cap I^-(p_0)$である。
(T1)$\Rightarrow$(T4)
自明
(T4)$\Rightarrow$(T3)
任意の$ p\in M$に対して、$ I^+(p)\cup I^-(p)=M$または$ M-{p}$となる。$ I^\pm(p)$はopenで、$ M,M-{p}$は連結だから、$ I^+(p)\cap I^-(p)\ne\emptyset$である。よって$ \exists r\in I^+(p)\cap I^-(p)$となる。従って、$ p<< r<< p$、特に$p<< p$である。
(V1)$\Leftrightarrow$(V2)
(T1)$\Leftrightarrow$(T2)と同様
(T1)$\Rightarrow$(V1)
自明
(V1)$\Rightarrow$(T1)
$ r\in I^+(p)$を1つとる。$ \forall q\in J^+(r)$より$ q\in I^+(p)$となる。同様に$ q\in I^-(p)$である。よって$ M=I^+(p)\cap I^-(p)$となる。
$I^\pm(p)$は常に開集合であるが、$J^\pm(p)$は一般には開でも閉でもないため、(T3),(T4)のtimelike曲線をcausal曲線に置き換えた主張(T3)',(T4)'はTVを意味しないことに注意してください。例えば、$M=\mathbb{R}\times S^1$とし、$\mathbb{R}$の座標を$t$、$S^1$の座標を$x$とするとき、計量を$g=-dtdx$で定めた時空$(M,g)$は(T3)',(T4)'を満たしますが、TVではありません。
Totally Viciousとなるための十分条件
次に気になるのは時空がいつTVとなるかということです。もちろん上の定義が必要十分なのですが、上の定義が成り立っているかを任意の時空に対して調べる方法を確立するのはかなり難しそうです。そこでもう少し調べやすそうな十分条件を調べることにします。
TVであることの十分条件として重要な役割を果たすのが、以下の反射律です。以下の定義からは自明ではないのですが反射律は因果構造が“連続的”であるということを意味しています。
時空$(M,g)$が点$q\in M$ において過去反射的(past reflecting)であるとは、次の同値な３つの条件を満たすときを言う。
$I^+(p)\supset I^+(q)\ \Rightarrow\ I^-(p)\subset I^-(q)$
$q\in \overline{I^+(p)}\ \Rightarrow\ p\in \overline{I^-(q)}$
$q\in \partial I^+(p)\ \Rightarrow\ p\in \partial I^-(q)$
さらに任意の点が過去反射的であるとき、時空$(M,g)$は過去反射的であるという。未来と過去を入れ替えて未来反射的も同様に定義する。過去反射的かつ未来反射的であるとき、時空$(M,g)$は反射的であるという。
次に$\overline{I^\pm(p)}$という集合について補題を準備しておきます。
$ \overline{I^+(p)}=\{r\in M;\ I^+(r)\subset I^+(p)\}$
$ T=\{r\in M;\ I^+(r)\subset I^+(p)\}$とする。
(i)$ \overline{I^+(p)}\subset T$を示す。
$ r\in \overline{I^+(p)}$に対して、$ I^+(r)\subset I^+(p)$を示せば良い。
$ r^+\in I^+(r)$に対して、$ I^-(r^+)$は$ r^+$の近傍だから、点列$ \{r_n\},r_n\to r$で大きい$ n$に対して、$ r_n\in I^-(r^+)\cap I^+(p)$となるものがある。よって$ p<< r_n<< r^+$であるから、$ r^+\in I^+(p)$となる。したがって$ I^+(r)\subset I^+(p)$である。
(ii)$ \overline{I^+(p)}\supset T$を示す。
$ T\ni r$を含む任意の近傍$ U$に対して、$ I^+(r,U)$は$ I^+(p)$に含まれるから、$ U\cap I^+(p)\ne\emptyset$となる。よって$ r\in \overline{I^+(p)}$である。
以上の準備から次の定理を示すことができます。
時空$(M,g)$がreflectingでかつ少なくとも１つCTCが存在するならば、TVである。
$ I^\pm(p_0)=\overline{I^\pm(p_0)}$が示されれば、$ I^\pm(p_0)$はopen & closedなので$ I^\pm(p_0)=M$より$ I^+(p_0)\cap I^-(p_0)=M$となりTVとなる。よって$ I^\pm(p_0)=\overline{I^\pm(p_0)}$を示せばよい。
$ I^\pm(p_0)\subset\overline{I^\pm(p_0)}$は明らかであるから、$ I^\pm(p_0)\supset\overline{I^\pm(p_0)}$を示す。
$ \gamma$をCTCとし、$ \gamma(0)=p_0,\gamma(u)=\gamma(u+1),\gamma(v)>>\gamma(u)\ (v>u)$であるとする。
$ r\in \overline{I^+(p_0)}$とすると、reflectivityより$ p_0\in \overline{I^-(r)}$となるから、補題１より$ I^-(p_0)\subset I^-(r)$である。
$ \gamma(-\epsilon)\subset I^-(r)$より$ I^+(\gamma(-\epsilon))\ni r$となる(ここまではreflectingなら$\gamma$がCTCでなくても常に成り立つ）。
$ \gamma(-\epsilon)=\gamma(1-\epsilon)\in I^+(p_0)$なので、$ r\in I^+(p_0)$となる。
（つまり$ p_0$の過去の未来に$ r$があり、CTCのおかげで$ p_0$の過去が未来にあるから$ r$が$ p_0$の未来にある。）
reflectingという性質は結構いろいろな時空で満たされるので強力である。以下の系が得られる。
時空$(M,g)$において、任意の$p\in M$に対して、$J^\pm(p)$がclosedであるとき、causally closedであるという。
この性質をcausally simpleと呼ぶ流儀もあります。私はcausalかつcausally closedな時空をcausally simpleと呼ぶ流儀です。
causally closed時空がCTCを持てばTVである。
$ p\in \overline{I^+(q)}(=\overline{J^+(q)})$のとき、causally closedならば$\overline{J^+(q)}=J^+(q)$であるから、$p\in J^+(q)$である。よって、同様の議論で$ q\in J^-(p)=\overline{I^-(p)}$となるから、reflectingである。よって定理２より主張が従う。
他にも次の便利な応用があります。
定常時空がCTCを持てばTVである。
https://mathlog.info/articles/3570 の命題９より定常時空はreflectingであるから、定理２より従う。
これは次のように応用できます。
Gödel宇宙はTVである。
Gödel宇宙の計量はPoincare model based座標において
$$
\begin{align}
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}+dz^2,
K=-\omega^2/2
\end{align}
$$
と表される。(
https://mathlog.info/articles/3471
)
$t=$一定面上に誘導される計量は
$$
\begin{align}
ds^2&=\frac{dr^2}{(1+\frac{K}{4}r^2)^2}+\left(\frac{r^2}{(1+\frac{K}{4}r^2)^2}-\frac{\omega^2}{4}\frac{r^4}{(1+\frac{K}{4}r^2)^2}\right)d\theta^2+dz^2 \\
&=\frac{dr^2}{(1+\frac{K}{4}r^2)^2}+\frac{r^2(1-\frac{\omega^2}{4}r^2)}{(1+\frac{K}{4}r^2)^2}d\theta^2+dz^2
\end{align}
$$
となるから、$t=$一定面上において、$||\partial_\theta||^2=\frac{r^2(1-\frac{\omega^2}{4}r^2)}{(1+\frac{K}{4}r^2)^2}$である。よって、$\partial_\theta$の積分曲線は閉曲線であり、さらに$2/\omega< r$の領域においてtimelikeである。したがってCTCが存在する。
コンパクト時空
コンパクト時空とTV時空との関係を述べます。まずコンパクト時空について基本的なことは以下です。
コンパクト時空$(M,g)$はCTCを持つ。
$M=\bigcup_{p\in M} I^+(p)$であり、コンパクトであることから有限集合$S=\{p_i\}$が存在して、$M=\bigcup_{p_i\in S} I^+(p_i)$となる。今$I^+(p_1)$が他の$I^+(p_i)$には含まれないとする（もし含まれるなら$S$から$p_1$を取り除けばよい）。よって$p$は他の$I^+(p_i)$には含まれない。従って$p_1\in I^+(p_1)$でなければならない。
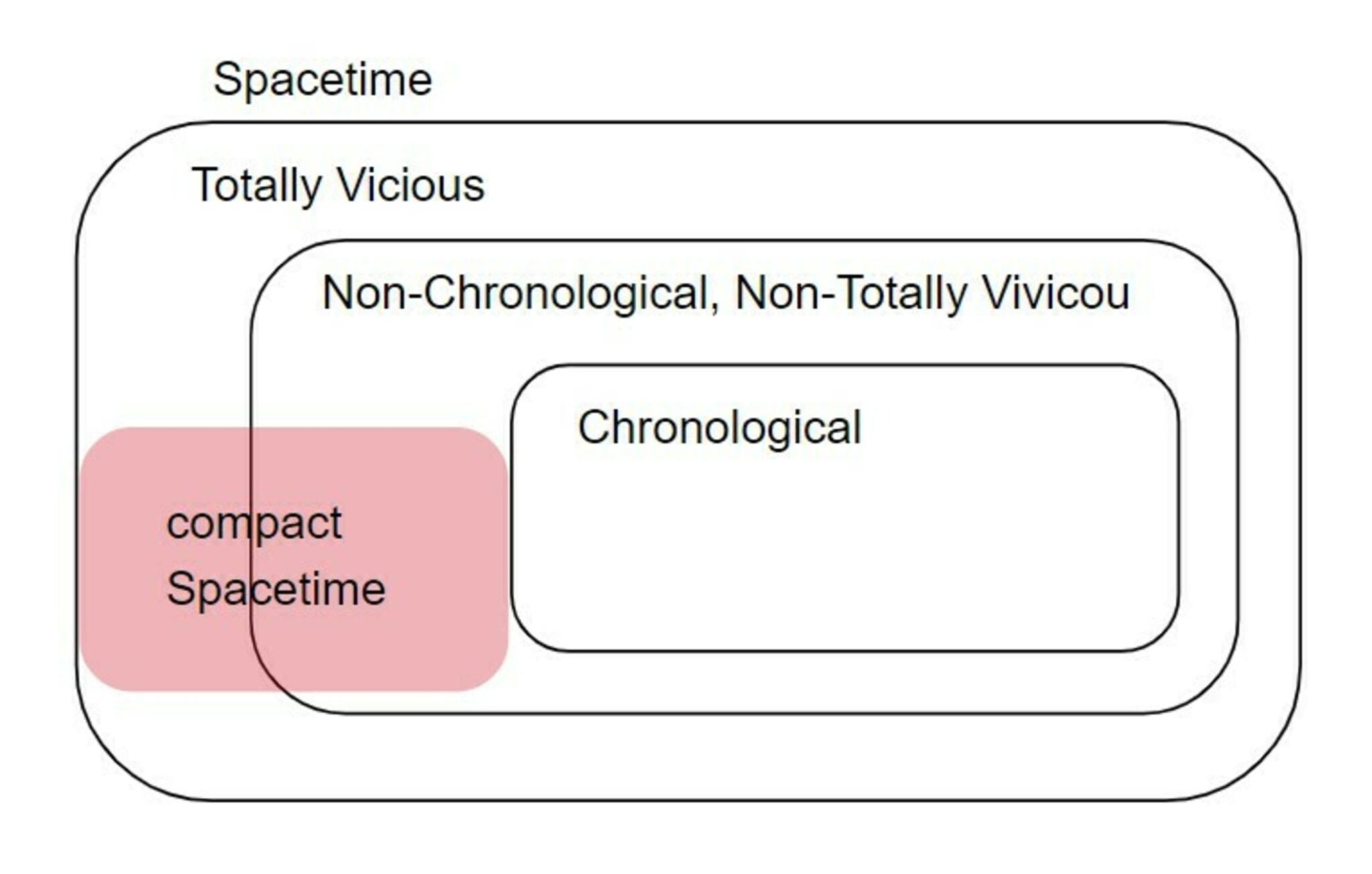因果構造の包含関係
このことからコンパクト時空はchronological時空ではありません。従って、Non-chronological Non-TV時空またはTV時空のどちらかとなります。コンパクトでNon-chronological Non-TVな時空の例として以下のものがあります。
$(\mathbb{R}^2,\{t,x\})$に次の計量を定める。
$$
g=\cos^2x(-dt^2+dx^2)+2\sin x dtdx
$$
これを$(t,x)\sim(t+1,x),(t,x)\sim(t,x+2\pi)$という同値類で割った2次元Lorentzianトーラス$(T^2,g)$を考える。
$$
g(\partial_t,\partial_t)=-\cos^2x,\ \nabla_{\partial_t}\partial_t=-\frac{\sin x\cos x}{\sin^2 x+\cos^4 x}(\sin x\partial_t+\cos^2 x\partial_x)
$$
であるから、$x=\pm\frac{\pi}{2}$において、$t-$曲線はnull測地線である。
また光円錐は下図のようになっている。
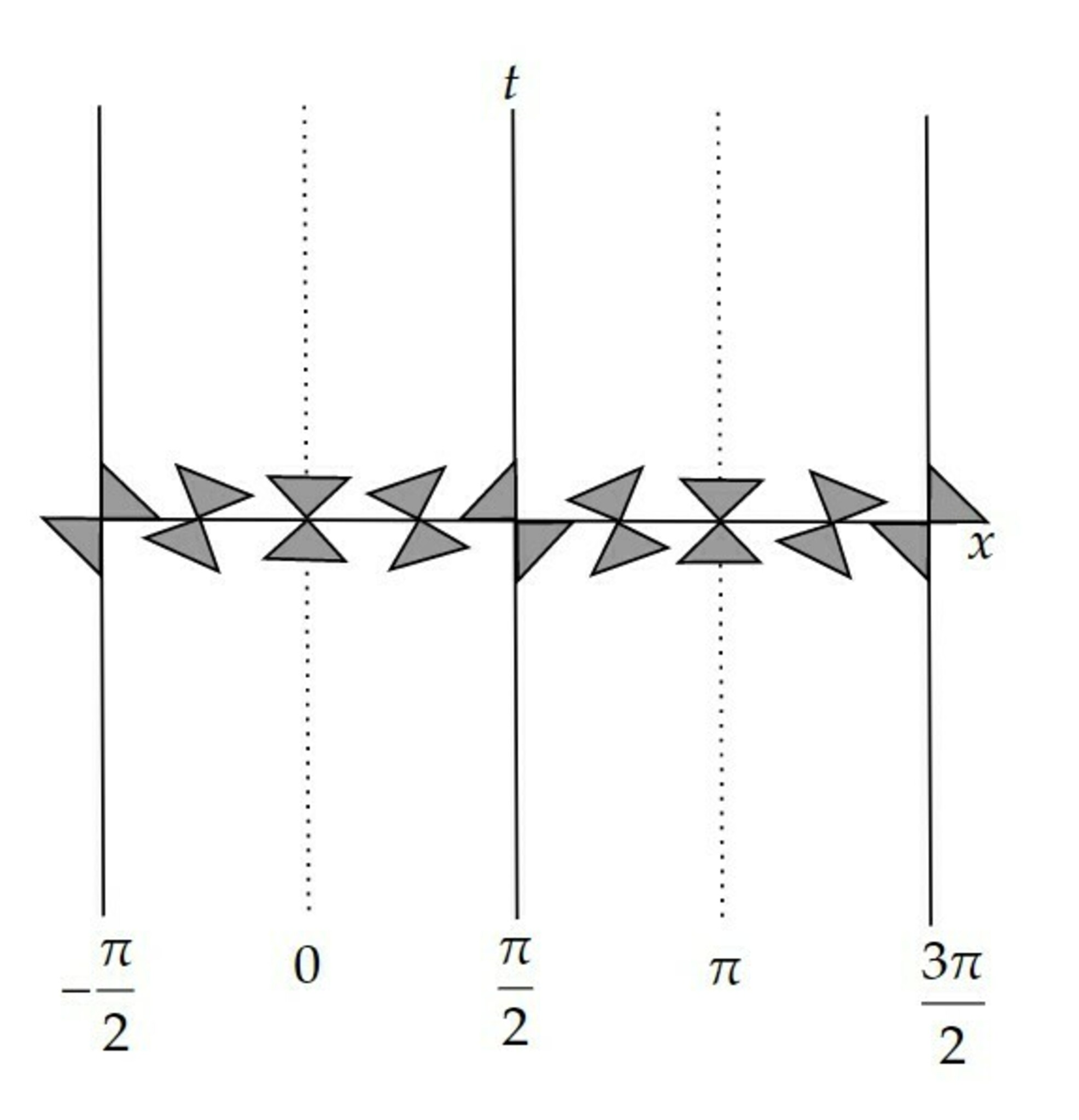(M,g)の光円錐
これより$p=(0,0)$に対して、$I^+(p)\subset \{(t,x);\ |x|<\pi/2\}$となることが分かるので、$(T^2,g)$はTVではない。
また$I^-(p)=M$が成り立つ。
上の例があることからコンパクト時空がいつTVとなるかという問題意識が当然生じます。TV時空がreflectingであることは自明なので、定理２、命題３を合わせると直ちに次が従います。
コンパクト時空$(M,g)$がreflectingであることと、TVであることは同値である。
https://mathlog.info/articles/4163 の命題２でhomogeneous時空はreflectingであることを示しました。従って次の系を得ます。
コンパクトなhomogeneous時空はTVである。
コンパクト時空においてはTVであることの判断はreflectingかどうかを調べればよいので少しやりやすくなった気がします。次の記事 全悪質時空２ ではreflectingを少し弱めたlocally reflectingとTVとの関係を考察します。