Proposition31~50の解説

\begin{eqnarray} y''y'-xy'y&=&0\\ \Rightarrow\int f(x)y''y'dx&=&\int xf(x)y'ydx \end{eqnarray}
\begin{eqnarray} (RHS)&=&\left[\frac12xf(x)y^2\right]-\int\frac12\left(f(x)+xf'(x)\right)y^2dx\\ (LHS)&=&\left[\frac12f(x)y'^2\right]-\int\frac12f'(x)y'^2dx \end{eqnarray}
\begin{eqnarray} y''y-xy^2&=&0\\ \Rightarrow\int f(x)y''ydx&=&\int xf(x)y^2dx \end{eqnarray}
\begin{eqnarray} (LHS)&=&\left[f(x)y'y\right]-\int(f(x)y'+f'(x)y)y'dx\\ &=&\left[f(x)y'y-\frac12f'(x)y^2\right]+\int\frac12f''(x)y^2-f(x)y'^2dx \end{eqnarray}
$f(x)=x^n$,積分区間を$[0,\infty)$とすると,
\begin{eqnarray} \int_0^{\infty}nx^{n-1}y'^2dx&=&\int_0^{\infty}(n+1)x^ny^2dx\\ \int_0^{\infty}x^{n}y'^2dx&=&\int_0^{\infty}\left(\frac{n(n-1)}{2}x^{n-2}-x^{n+1}\right)y^2dx \end{eqnarray}
がわかるので,
\begin{eqnarray} (2n+1)\int_0^{\infty}x^ny^2dx-\frac{n(n-1)(n-2)}{2}\int_0^{\infty}x^{n-3}y^2dx=0 \end{eqnarray}
$I(n):=\int_0^{\infty}x^{n}y^2dx$とすると,
\begin{eqnarray} \frac{\Gamma(n+w+\frac{7}{6})12^n}{(3n+w)!}I(3n+w)-\frac{\Gamma(n+w+\frac16)12^n}{(3n+w-3)!}I(3n+w-3)=0 \end{eqnarray}
\begin{align} \therefore I(3n+w)=\frac{(3n+w)!\Gamma(w+\frac76)}{\Gamma(n+w+\frac{7}{6})12^n}I(w) \end{align}
がわかりました.$I(0)$については,
\begin{eqnarray} \int Ai(x)^2dx&=&xAi(x)^2-Ai'(x)^2\\ \therefore\int_0^{\infty}Ai(x)^2dx&=&Ai'(0)^2=\frac{1}{3^{2/3}\Gamma(\frac{1}{3})^2} \end{eqnarray}
なので,題意が示されました.

\begin{align} g(s):=\int_{-\infty}^{\infty}Ai(x)e^{sx}dx \end{align}
\begin{eqnarray} y''-xy&=&0\\ \Rightarrow\int_{-\infty}^{\infty}y''e^{sx}dx&=&\int_{-\infty}^{\infty}xye^{sx}dx \end{eqnarray}
\begin{eqnarray} (RHS)&=&g'(s)\\ (LHS)&=&[y'e^{sx}]_{-\infty}^{\infty}-s\int_{-\infty}^{\infty}y'e^{sx}dx\\ &=&s^2\int_{-\infty}^{\infty}ye^{sx}dx=s^2g(s) \end{eqnarray}
\begin{align} \therefore s^2g-g'=0,g(0)=1 \Leftrightarrow g(s)=e^{s^3/3} \end{align}

\begin{align} h(s):=\int_{-\infty}^{\infty}Ai(x)^2e^{sx}dx \end{align}
prop31の$f(x)$の不定積分について,$f(x)=e^{sx}$,積分区間を$(-\infty,\infty)$とすると,
\begin{eqnarray} \int_{-\infty}^{\infty}sy'^2e^{sx}dx&=&\int_{-\infty}^{\infty}(1+sx)y^2e^{sx}dx=h(s)+sh'(s)\\ \int_{-\infty}^{\infty}y'^2e^{sx}&=&\int_{-\infty}^{\infty}\left(\frac{s^2}{2}-x\right)y^2e^{sx}dx=\frac{s^2}{2}h(s)-h'(s) \end{eqnarray}
\begin{eqnarray} \therefore \frac{s^3}{2}h-sh'&=&h+sh' \end{eqnarray}
\begin{eqnarray} 2sh'+\left(1-\frac{s^3}{2}\right)h=0\Rightarrow h(s)=\frac{e^{(s^3-1)/12}}{\sqrt s}h(1) \end{eqnarray}
そして,
\begin{eqnarray} h(1)&=&\int_{-\infty}^{\infty}e^xAi(x)\int_{-\infty}^{\infty}e^{\frac{(2\pi k)^3}{3}i+2\pi ikx}dkdx\\ &=&\int_{-\infty}^{\infty}e^{\frac{(2\pi k)^3}{3}i+\frac{(2\pi ik+1)^3}{3}}dk\\ &=&\int_{-\infty}^{\infty}e^{-4\pi^2k^2+2\pi ik+\frac{1}{3}}dk\\ &=&\frac{1}{2\sqrt{\pi}}e^{1/12} \end{eqnarray}
なので,
\begin{align} h(s)=\frac{1}{2\sqrt{s\pi}}e^{s^3/12} \end{align}
です.

\begin{eqnarray} \int_{0}^X\frac{1-e^{nit}}{1-e^{it}}f(t)dt&=&\int_0^X\sum_{k=0}^{n-1}e^{kit}f(t)dt\\ &=&\sum_{k=0}^{n-1}\int_0^Xe^{kit}f(t)dt\\ \end{eqnarray}
なので,$n\to\infty$としたとき,
\begin{align} \int_0^X\frac{e^{nit}}{1-e^{it}}f(t)dt=0 \end{align}
が成り立てば題意が成り立ちます.
\begin{eqnarray} \int_0^{X}e^{nit}\frac{f(t)}{1-e^{it}}dt&=&\left[\frac{e^{nit}}{ni}\frac{f(t)}{1-e^{it}}\right]_0^X-\frac1{ni}\int_0^Xe^{nit}\frac{d}{dt}\left(\frac{f(t)}{1-e^{it}}\right)dt\\ &=&\frac{1}{ni}\left(e^{niX}\frac{f(X)}{1-e^{iX}}-\lim_{t\to0}\frac{f(t)}{t}\frac{t}{1-e^{it}}\right)-\frac{1}{ni}\int_0^Xe^{nit}\frac{d}{dt}\left(\frac{f(t)}{1-e^{it}}\right)dt \end{eqnarray}
です.$\frac{1}{1-e^{it}}$は$t=0$で不連続ですが,$\lim_{t\to0}\frac{f(t)}{t}$が存在することと,$\lim_{t\to0}\frac{t}{1-e^{it}}$が存在することから,$\frac{f(t)}{1-e^{it}}$は$t\in(0,X]$で有界で連続です.
有界で連続な関数の導関数もまた有界で連続なので,$\int_0^Xe^{nit}\frac{d}{dt}\left(\frac{f(t)}{1-e^{it}}\right)dt$は有限の値になります.
以上より,$\int_0^Xe^{nit}\frac{f(t)}{1-e^{it}}dt=O(\frac{1}{n})$なので,題意が成り立ちます.

\begin{eqnarray} \int_0^{\infty}\frac{2x}{1+x^2}\ln\frac{x^2+2x\cos a+1}{x^2+2x\cos b+1}dx&=&\int_0^{\infty}\frac{2x}{1+x^2}\int_b^{a}\frac{-2x\sin t}{x^2+2x\cos t+1}dtdx \end{eqnarray}
\begin{eqnarray} \int_0^{\infty}\frac{4x^2}{(x^2+1)(x^2+2x\cos t+1)}dx&=&\int_0^{\infty}\left(\frac{1}{x^2+1}-\frac{1}{x^2+2x\cos t+1}\right)\frac{2x}{\cos t}dx\\ &=&\frac{1}{\cos t}\int_0^{\infty}\frac{2x}{x^2+1}-\frac{2x+2\cos t}{x^2+2x\cos t+1}+\frac{2\cos t}{x^2+2x\cos t+1}dx\\ &=&\frac{1}{\cos t}\left[\ln\frac{x^2+1}{x^2+2x\cos t+1}+2\cot t\ \tan^{-1}\frac{x+\cos t}{\sin t}\right]_0^{\infty}\\ &=&\frac{2t}{\sin t}\ \ (|t|\in(0,\pi/2]) \end{eqnarray}
なので,
\begin{eqnarray} \int_0^{\infty}\frac{2x}{x^2+1}\ln\frac{x^2+2x\cos a+1}{x^2+2x\cos b+1}dx&=&\int_b^{a}\int_0^{\infty}\frac{-4x^2\sin t}{(x^2+1)(x^2+2x\cos t+1)}dxdt\\ &=&\int_a^b2tdt=b^2-a^2 \end{eqnarray}
となります.

\begin{eqnarray} \int_0^1\ln\left(\frac{1+x+\frac{x^2}{4}}{1+x-2x^2}\right)\frac{dx}{x(2+x)}&=&\int_0^1\ln\left(\frac{4+4x+x^2}{4+4x-8x^2}\right)\frac{dx}{x(2+x)}\\ &=&\int_0^1\ln\left(\frac{(2+x)^2}{(2+x)^2-(3x)^2}\right)\frac{dx}{x(2+x)}\\ &=&-\int_0^1\ln\left(1-\left(\frac{3x}{2+x}\right)^2\right)\frac{dx}{x(2+x)}\\ &=&\frac14\int_0^1\frac{\ln(\frac{1}{1-X})}{X}dX\ \ \left(\left(\frac{3x}{2+x}\right)^2\to X\right)\\ &=&\frac{\pi^2}{24}\\ \int_0^1\ln\left(\frac{1+2x+x^2}{1+2x-3x^2}\right)\frac{dx}{x(1+x)}&=&\int_0^1\ln\left(\frac{(1+x)^2}{(1+x)^2-(2x)^2}\right)\frac{dx}{x(1+x)}\\ &=&-\int_0^1\ln\left(1-\left(\frac{2x}{1+x}\right)^2\right)\frac{dx}{x(1+x)}\\ &=&\frac{1}{2}\int_0^1\frac{\ln\frac{1}{1-X}}{X}dX\ \ \left(\left(\frac{2x}{1+x}\right)^2\to X\right)\\ &=&\frac{\pi^2}{12} \end{eqnarray}

\begin{eqnarray} \int_0^1\frac{1-\sqrt{1-s^2x^2}}{x\sqrt{1-x^2}\sqrt{1-s^2x^2}}\ln\frac{1}{1-x^2}dx&=&\int_0^1\left(\frac{1}{\sqrt{1-s^2x^2}}-1\right)\ln\frac{1}{1-x^2}\frac{dx}{x\sqrt{1-x^2}}\\ &=&\sum_{n\gt0}\beta_n s^{2n}\int_0^1x^{2n-1}\frac{\ln\frac{1}{1-x^2}}{\sqrt{1-x^2}}dx\\ &=&\sum_{n\gt k\geq0}\frac{s^{2n}}{n(2k+1)} \end{eqnarray}
以前 僕の記事 で書いたこのモーメントを用いました.
\begin{align} \int_0^1x^{2n-1}\frac{\ln\frac{1}{1-x^2}}{\sqrt{1-x^2}}dx=\frac{1}{2n\beta_n}\sum_{k=0}^{n-1}\frac{1}{k+\frac{1}{2}} \end{align}
あとは,$(\tanh^{-1}x)^2$の母関数について考えて一致することを確かめればよいです.
\begin{eqnarray} (\tanh^{-1}x)^2&=&\left(\int_0^x\frac{dt}{1-t^2}\right)^2\\ &=&2!\int_{x\gt s\gt t\gt0}\frac{ds}{1-s^2}\frac{dt}{1-t^2}\\ &=&2\sum_{n,m\geq0}\int_{x\gt s\gt t\gt0}s^{2n}t^{2n}dsdt\\ &=&\sum_{n,m\geq0}\frac{x^{2n+2m+2}}{(2n+1)(n+m+1)}\\ &=&\sum_{n\gt k\geq0}\frac{x^{2n}}{n(2k+1)} \end{eqnarray}
以上より,
\begin{align} \int_0^{1}\frac{1-\sqrt{1-s^2x^2}}{x\sqrt{1-x^2}\sqrt{1-s^2x^2}}\ln\frac{1}{1-x^2}dx=(\tanh^{-1}s)^2 \end{align}
です.

\begin{eqnarray} \frac{d}{ds}\int_0^1\frac{\ln(1-sx)}{x}\ln\frac{1-x}{\sqrt{1-sx}}dx&=&\int_0^1\frac{\ln(1-sx)}{1-sx}-\frac{\ln(1-x)}{1-sx}\ dx\\ &=&-\frac{\ln^2(1-s)}{2s}-\int_0^1\frac{\ln(1-x)}{1-sx}dx \end{eqnarray}
\begin{eqnarray} \int_0^1\frac{\ln\frac{1}{1-x}}{1-sx}dx&=&\sum_{n\geq0}s^n\int_0^1x^n\ln\frac{1}{1-x}dx \end{eqnarray}
であり,次が成り立つので,(証明は後述)
\begin{align} \int_0^1x^{n-1}\ln\frac{1}{1-x}dx=\frac{1}{n}\sum_{k=1}^n\frac{1}{k} \end{align}
\begin{eqnarray} \int_0^1\frac{\ln\frac{1}{1-x}}{1-sx}dx&=&\sum_{n\geq k\gt0}\frac{s^{n-1}}{nk}\\ &=&\frac{1}{s}\mathrm{Li}_2(s)+\sum_{n,m\geq0}\frac{s^{n+m+1}}{(n+m+2)(n+1)}\\ &=&\frac{1}{s}\mathrm{Li}_2(s)+\sum_{n,m\geq0}\left(\frac{1}{n+1}-\frac{1}{n+m+2}\right)\frac{s^{n+m+1}}{n+1}\\ &=&\frac{1}{s}\mathrm{Li}_2(s)+\frac{\ln^2(1-s)}{2s} \end{eqnarray}
となります.最後に$A=B-A\Leftrightarrow A=\frac12B$と$\ln^2(1-x)=\sum_{n,m\geq0}\frac{s^{n+1}}{n+1}\frac{s^{m+1}}{m+1}$を用いました.
\begin{eqnarray} \int_0^1\frac{\ln(1-sx)}{x}\ln\frac{1-x}{\sqrt{1-sx}}dx&=&\int_0^s\left(-\frac{\ln^2(1-s)}{2s}-\int_0^1\frac{\ln(1-x)}{1-sx}dx\right)ds\\ &=&\int_0^s\frac{1}{s}\mathrm{Li}_2(s)ds\\ &=&\mathrm{Li}_3(s) \end{eqnarray}
これにより題意が示されました.

\begin{eqnarray} \int_0^1\frac{\tanh^{-1}x}{1-x^2}(\tan^{-1}sx-x\tan^{-1}s)dx&=&\int_0^1\frac{\tanh^{-1}x}{1-x^2}\int_0^s\frac{x}{1+x^2t^2}-\frac{x}{1+t^2}dtdx\\ &=&\int_0^s\int_0^1\frac{\tanh^{-1}x}{1-x^2}\frac{xt^2(1-x^2)}{(1+x^2t^2)(1+t^2)}dxdt\\ &=&\int_0^s\frac{t^2}{1+t^2}\int_0^1\frac{x\tanh^{-1}x}{1+x^2t^2}dxdt\\ &=&\int_0^s\frac{t^2}{1+t^2}\sum_{n\geq0}(-1)^{n}t^{2n}\int_0^1x^{2n+1}\tanh^{-1}xdxdt\\ &=&\int_0^s\frac{1}{1+t^2}\sum_{n\gt k\geq0}(-1)^{n-1}\frac{t^{2n}}{2n}\frac{1}{2k+1}dt \end{eqnarray}
ここで,
\begin{eqnarray} (\tan^{-1}t)^2&=&\left(\int_0^t\frac{dx}{1+x^2}\right)^2\\ &=&2!\int_{t\gt x\gt y\gt0}\frac{dx}{1+x^2}\frac{dy}{1+y^2}\\ &=&2\sum_{n,m\geq0}(-1)^{n+m}\int_{t\gt x\gt y\gt0}x^{2n}y^{2m}dxdy\\ &=&\sum_{n,m}(-1)^{n+m}\frac{t^{2n+2m+2}}{(n+m+1)(2m+1)}\\ &=&\sum_{n\gt k\geq0}(-1)^{n}\frac{t^{2n}}{n(2k+1)} \end{eqnarray}
なので,
\begin{eqnarray} \int_0^1\frac{\tanh^{-1}x}{1-x^2}(\tan^{-1}sx-x\tan^{-1}s)dx&=&\int_0^s\frac{1}{1+t^2}\frac{(\tan^{-1}t)^2}{2}dt\\ &=&\frac{1}{6}(\tan^{-1}s)^3 \end{eqnarray}
となります.

\begin{eqnarray} \int_0^{\infty}\sin\left(\frac{a\pi x}{2}\right)\left(\psi\left(\frac{3+x}{4}\right)-\psi\left(\frac{1+x}{4}\right)\right)dx&=&\int_0^{\infty}\sin\left(\frac{a\pi x}{2}\right)\sum_{n\geq0}\frac{4(-1)^n}{2n+1+x}dx\\ &=&4\sum_{n\geq0}(-1)^n\int_0^{\infty}\frac{\sin\frac{a\pi x}{2}}{2n+1+x}dx\\ &=&4\sum_{n\geq0}(-1)^n\int_0^{\infty}\sin\frac{a\pi x}{2}\int_0^{\infty}e^{-(2n+1+x)u}dudx\\ &=&\mathrm{Im}\ 4\sum_{n\geq0}(-1)^n\int_0^{\infty}e^{-(2n+1)u}\int_0^{\infty}e^{-(u-\frac{a\pi}{2}i)x}dxdu\\ &=&2a\pi\sum_{n\geq0}(-1)^{n}\int_0^{\infty}\frac{e^{-(2n+1)u}}{u^2+\frac{a^2\pi^2}{4}}du\left(=2\int_0^{\infty}\frac{1}{x^2+1}\frac{dx}{\cosh\frac{a\pi x}{2}}\right)\\ &=&\frac{2}{a\pi}\sum_{n\geq0}\int_0^{\infty}\frac{(-1)^n(2n+1)}{\frac{x^2}{a^2\pi^2}+\left(n+\frac{1}{2}\right)^2}e^{-x}dx\\ &=&\frac{2}{a}\int_0^{\infty}\frac{1}{\cosh\frac{x}{a}}e^{-x}dx\\ &=&\frac{4}{a}\sum_{n\geq0}\int_0^{\infty}(-1)^ne^{-\left(1+\frac{2n+1}{a}\right)x}dx\\ &=&4\sum_{n\geq0}\frac{(-1)^n}{2n+1+a}\\ &=&\psi\left(\frac{3+a}{4}\right)-\psi\left(\frac{1+a}{4}\right) \end{eqnarray}

$a\gt 0$とします.
\begin{eqnarray} \int_{-\infty}^{\infty}\frac{\cos\left(s\tan^{-1}\frac{x}{a}\right)}{(a^2+x^2)^{s/2}}\frac{dx}{1+x^2}&=&2\int_0^{\infty}\frac{\cos\left(s\tan^{-1}\frac{x}{a}\right)}{(a^2+x^2)^{s/2}}\frac{dx}{1+x^2}\\ &=&\mathrm{Re}\ 2\int_0^{\infty}\frac{1}{(a-ix)^s}\frac{dx}{1+x^2}\\ &=&\mathrm{Re}\ \frac{2}{\Gamma(s)}\int_0^{\infty}\frac{dx}{1+x^2}\int_0^{\infty}t^{s-1}e^{-(a-ix)t}dt\\ &=&\frac{2}{\Gamma(s)}\int_0^{\infty}t^{s-1}e^{-at}\int_0^{\infty}\frac{\cos xt}{1+x^2}dxdt\\ &=&\frac{\pi}{\Gamma(s)}\int_0^{\infty}t^{s-1}e^{-(1+a)t}dt\\ &=&\frac{\pi}{(1+a)^s}\\ \int_{-\infty}^{\infty}\frac{\sin\left(s\tan^{-1}\frac{x}{a}\right)}{(a^2+x^2)^{s/2}}\frac{x}{1+x^2}dx&=&2\int_0^{\infty}\frac{\sin\left(s\tan^{-1}\frac{x}{a}\right)}{(a^2+x^2)^{s/2}}\frac{x}{1+x^2}dx\\ &=&\mathrm{Im}\ 2\int_0^{\infty}\frac{1}{(a-ix)^s}\frac{x}{1+x^2}dx\\ &=&\mathrm{Im}\ \frac{2}{\Gamma(s)}\int_0^{\infty}\frac{x}{1+x^2}\int_0^{\infty}t^{s-1}e^{-(a-ix)t}dtdx\\ &=&\frac{2}{\Gamma(s)}\int_0^{\infty}t^{s-1}e^{-at}\int_0^{\infty}\frac{x\sin xt}{1+x^2}dxdt\\ &=&\frac{\pi}{\Gamma(s)}\int_0^{\infty}t^{s-1}e^{-(1+a)t}dt\\ &=&\frac{\pi}{(1+a)^s} \end{eqnarray}

\begin{eqnarray} f_1(s):&=&\int_0^{\infty}\frac{x}{e^x-1}e^{-sx}dx\\ &=&\sum_{n\geq0}\int_0^{\infty}xe^{-(s+n+1)x}dx=\sum_{n\geq0}\frac{1}{(n+s+1)^2}\\ f_2(s):&=&\int_0^{\infty}\left(\frac{x}{e^x-1}-1\right)\frac{e^{-sx}}{x}dx\\ &=&\int_s^{\infty}f_1(t)-\frac{1}{t}dt\\ &=&\left[-\ln t-\sum_{n\geq0}\frac{1}{n+t}+\frac{1}{t}\right]_s^{\infty}\\ &=&\ln s-\psi(s)-\frac{1}{s}\\ f_3(s):&=&\int_0^{\infty}\left(\frac{x}{e^x-1}-1+\frac{x}{2}\right)\frac{e^{-sx}}{x^2}dx\\ &=&\int_s^{\infty}f_2(t)+\frac{1}{2t}dt\\ &=&\left[\left(t-\frac12\right)\ln t-t-\ln\Gamma(t)\right]_s^{\infty}\\ &=&\ln\frac{\Gamma(s)e^s}{s^{s-1/2}}+\lim_{t\to\infty}\ln\frac{t^{t-1/2}}{\Gamma(t)e^t}\\ &=&\ln\frac{\Gamma(s)e^s}{s^{s-1/2}\sqrt{2\pi}} \end{eqnarray}

\begin{eqnarray} \int_0^{1}\frac{\tan^{-1}\frac{1}{\sqrt{x^2+2a^2}}}{\sqrt{x^2+2a^2}(x^2+a^2)}dx&=&\int_0^{1}\int_0^1\frac{dydx}{(x^2+y^2+2a^2)(x^2+a^2)}\\ &=&\int_0^1\int_0^1\left(\frac{1}{x^2+a^2}-\frac{1}{x^2+y^2+2a^2}\right)\frac{dxdy}{y^2+a^2}\\ &=&\left(\int_0^1\frac{dx}{x^2+a^2}\right)^2-\int_0^1\frac{dxdy}{(x^2+y^2+2a^2)(y^2+a^2)}\\ &=&\frac{1}{2}\left(\int_0^1\frac{dx}{x^2+a^2}\right)^2\\ &=&\frac1{2a^2}\left(\tan^{-1}\frac{1}{a}\right)^2 \end{eqnarray}

$g(x):=\int_0^xg'(y)dy$に対して
\begin{eqnarray} \int_0^1f(x)g(x)dx&=&\int_0^1f(x)\int_0^{x}g'(y)dydx\\ &=&\int_0^1g'(y)\int_y^1f(x)dxdy\\ &=&\int_0^1g'(y)(f^{(-1)}(1)-f^{(-1)}(y))dy \end{eqnarray}
なので,
\begin{eqnarray} \int_0^1\mathrm{Li}_2(x)\ln\frac{1}{1-x}dx&=&\int_0^1\frac{1-x}{x}\left(\ln(1-x)-1\right)\ln(1-x)dx\\ &=&\int_0^1\ln x-\ln^2x+\frac{\ln\frac{1}{1-x}}{x}+\frac{\ln^2\frac{1}{1-x}}{x}dx\\ &=&-3+\int_0^1\frac{dx}{x}\int_0^x\frac{dy}{1-y}+2!\int_0^1\frac{dx}{x}\int_0^x\frac{dy}{1-y}\int_0^z\frac{dz}{1-z}\\ &=&\zeta(2)-3+2\int_0^1\frac{dz}{z}\int_0^z\frac{dy}{y}\int_0^x\frac{dx}{1-x}\\ &=&\zeta(2)+2\zeta(3)-3 \end{eqnarray}
です.

先ず,
\begin{eqnarray} \int_0^{\infty}\frac{\tan^{-1}\frac{1}{x}(\tan^{-1}x)^2}{x}dx&=&\int_0^{\pi/2}\frac{\left(\frac{\pi}{2}-x\right)x^2}{\sin x\cos x}dx\ \ (x\to\tan x)\\ &=&\int_0^{\pi/2}\frac{(\pi-2x)x^2}{\sin 2x}dx\\ &=&\frac{1}{8}\int_0^{\pi}\frac{(\pi-x)x^2}{\sin x}dx\\ &=&\frac{1}{8}\left(\int_0^{\pi/2}+\int_{\pi/2}^{\pi}\right)\ ''dx\\ &=&\frac{1}{8}\left(\int_0^{\pi/2}\frac{(\pi-x)x^2}{\sin x}dx+\int_0^{\pi/2}\frac{t(\pi-t)^2}{\sin t}dt\right)\ \ (\pi-x\to t)\\ &=&\frac{\pi}{8}\int_0^{\pi/2}\frac{(\pi-x)x}{\sin x}dx\\ &=&\frac{7\pi}{16}\zeta(3) \end{eqnarray}
です.
そして,$x\gt0$において
\begin{eqnarray} \ln^2(1+xi)&=&\left(\frac{1}{2}\ln(1+x^2)+i\tan^{-1}x\right)^2\\ &=&\left(\frac{1}{4}\ln^2(1+x^2)-(\tan^{-1}x)^2\right)+i\ln(1+x^2)\tan^{-1}x \end{eqnarray}
と,prop40より,
\begin{eqnarray} \int_0^{\infty}\frac{\cos(s\tan^{-1}x)}{(1+x^2)^{s/2}}\frac{a}{a^2+x^2}dx&=&\frac{\pi}{2}\frac{1}{(1+a)^s}\\ \mathrm{Re}\int_0^{\infty}(1+ix)^{-s}\frac{a}{a^2+x^2}dx&=& \end{eqnarray}
ですから,両辺$s$で2階微分し$s\to+0$とすれば,
\begin{eqnarray} \mathrm{Re}\int_0^{\infty}\ln^2(1+ix)\frac{a}{a^2+x^2}dx&=&\frac{\pi}{2}\ln^2(1+a)\\ \int_0^{\infty}\frac{\frac{1}{4}\ln^2(1+x^2)-(\tan^{-1}x)^2}{a^2+x^2}dx&=&\frac{\pi}{2}\frac{\ln^2(1+a)}{a} \end{eqnarray}
がわかります.
prop15,43でも用いた,$\int_0^{1}\frac{da}{a^2+x^2}=\frac{1}{x}\tan^{-1}\frac{1}{x}$を使えば,
\begin{eqnarray} \int_0^{\infty}\frac{\tan^{-1}\frac{1}{x}}{x}\left(\frac{1}{4}\ln^2(1+x^2)-(\tan^{-1}x)^2\right)dx&=&\frac{\pi}{2}\int_0^{1}\frac{\ln^2(1+a)}{a}da\\ &=&\pi\int_0^1\frac{da}{a}\int_0^a\frac{db}{1+b}\int_0^b\frac{dc}{1+c}\\ &=&\pi\sum_{n,m\geq0}\frac{(-1)^{n+m}}{(n+1)(n+m+2)^2}=\pi\zeta(1,\bar{2})=\frac{\pi}{8}\zeta(3) \end{eqnarray}
であり,$\int_0^{\infty}\tan^{-1}\frac{1}{x}(\tan^{-1}x)^2\frac{dx}{x}=\frac{7\pi}{16}\zeta(3)$ですから,
\begin{eqnarray} \int_0^{\infty}\frac{\tan^{-1}\frac{1}{x}\ln^2(1+x^2)}{x}dx=\frac{9\pi}{4}\zeta(3) \end{eqnarray}
となります.

\begin{eqnarray} \int_0^1\frac{dx}{\sqrt{1+x^4}}&=&\int_0^1\frac{dx}{2\sqrt{x(1+x^2)}}\\ &=&\int_0^1\frac{dx}{\sqrt{(1-x^2)((1+x)^2+(1-x)^2)}}\ \left(x\to\frac{1-x}{1+x}\right)\\ &=&\frac{1}{\sqrt2}\int_0^1\frac{dx}{\sqrt{1-x^4}}\\ &=&\frac{\pi^{3/2}}{4\Gamma(\frac{3}{4})^2} \end{eqnarray}

\begin{eqnarray} \int_0^{\pi/2}(\sinh^{-1}\sin x)^2dx&=&\int_0^{1}\frac{(\sinh^{-1}x)^2}{\sqrt{1-x^2}}dx\\ &=&2!\int_0^1\frac{dx}{\sqrt{1-x^2}}\int_0^x\frac{dy}{\sqrt{1+y^2}}\int_0^z\frac{dz}{\sqrt{1+z^2}}\\ &=&2!\int_0^1\frac{dx}{\sqrt{1-x^2}}\int_0^x\frac{dy}{\sqrt{1+y^2}}(-1)^0\beta_0\sum_{n\gt0}\frac{(-1)^{n-1}}{2n\beta_n}y^{2n-1}\sqrt{1+y^2}dy\\ &=&2\sum_{n\gt0}\frac{(-1)^{n-1}}{2n\beta_n}\int_0^1\frac{dx}{\sqrt{1-x^2}}\int_0^xy^{2n-1}dy\\ &=&\sum_{n\gt0}\frac{(-1)^{n-1}}{2n^2\beta_n}\int_0^1\frac{x^{2n}}{\sqrt{1-x^2}}dx\\ &=&\frac{\pi}{4}\sum_{n\gt0}\frac{(-1)^{n-1}}{n^2}=\frac{\pi^3}{48}\\ \int_0^{\pi/2}\left(\sinh^{-1}\sqrt{\sin x}\right)^3dx&=&2\int_0^1\frac{x(\sinh^{-1}x)^3}{\sqrt{1-x^4}}dx\\ &=&12\int_0^1\frac{x}{\sqrt{1-x^4}}dx\int_0^x\frac{dy}{\sqrt{1+y^2}}\int_0^y\frac{dz}{\sqrt{1+z^2}}\int_0^z\frac{dw}{\sqrt{1+w^2}}\\ &=&12\int_0^1\frac{x}{\sqrt{1-x^4}}dx\int_0^y\frac{dy}{\sqrt{1+y^2}}\int_0^y\frac{dz}{\sqrt{1+z^2}}\sum_{n\gt0}\frac{(-1)^{n-1}}{2n\beta_n}z^{2n-1}\sqrt{1+z^2}\\ &=&12\int_0^1\frac{x}{\sqrt{1-x^4}}dx\int_0^y\sum_{n\gt0}\frac{(-1)^{n-1}}{(2n)^2\beta_n}\frac{y^{2n}}{\sqrt{1+y^2}}dy\\ &=&3\sum_{m\gt n\gt0}\frac{(-1)^{n}}{2n\beta}\frac{1}{m^2}\int_0^1\frac{x^{2n}}{\sqrt{1-x^2}}dx\\ &=&\frac{3\pi}{4}\sum_{m\gt n\gt0}\frac{(-1)^m}{mn^2}=\frac{3\pi}{4}\zeta(\bar{1},2)\\ &=&\frac{3\pi}{4}\left(\frac{\pi^2}{12}\ln2-\frac{1}{4}\zeta(3)\right)\\ &=&\frac{\pi^3}{16}\ln2-\frac{3\pi}{16}\zeta(3) \end{eqnarray}

\begin{eqnarray} \int_0^{\pi/2}\ln\frac{1+\cos x}{\sin x}\ln\ln\frac{1+\cos x}{\sin x}\frac{dx}{1+\sin x}&=&\int_0^1\ln\frac{1+\sqrt{1-x^2}}{x}\ln\ln\frac{1-\sqrt{1-x^2}}{x}\frac{dx}{(x+1)\sqrt{1-x^2}}\\ &=&\int_0^1\cosh^{-1}\frac{1}{x}\ln\cosh^{-1}\frac{1}{x}\frac{dx}{(x+1)\sqrt{1-x^2}}\\ &=&\int_0^{\infty}\frac{x\ln x}{\cosh x+1}dx \end{eqnarray}
次のMellin変換を考えます.
\begin{eqnarray} \int_0^{\infty}\frac{x^{s-1}}{\cosh x+\cos t}dx&=&\int_0^{\infty}x^{s-1}\frac{2}{\sin t}\sum_{n\gt0}(-1)^{n-1}\sin(nt) e^{-nx}dx\\ &=&\frac{2}{\sin t}\sum_{n\gt0}(-1)^{n-1}\sin(nt)\frac{\Gamma(s)}{n^s} \end{eqnarray}
故に,
\begin{eqnarray} \int_0^{\infty}\frac{x^{s-1}}{\cosh x+\cos t}\ln x\ dx&=&\frac{d}{ds}\int_0^{\infty}\frac{x^{s-1}}{\cosh x+\cos t}dx\\ &=&2\sum_{n\gt0}(-1)^{n-1}\frac{\sin nt}{\sin t}\frac{\Gamma(s)}{n^s}(\psi(s)-\ln n) \end{eqnarray}
であり,$\lim_{t\to0}\frac{\sin nt}{\sin t}=n$より,
\begin{eqnarray} \int_0^{\infty}\frac{x\ln x}{\cosh x+1}dx&=&2\sum_{n\gt0}\frac{(-1)^{n-1}}{n}(\psi(2)-\ln n)\\ &=&2\ln2\psi(2)+2\sum_{n\gt0}\frac{(-1)^n}{n}\ln n \end{eqnarray}
です.
\begin{eqnarray} \left[\frac{d}{ds}\sum_{n\gt0}\frac{(-1)^{n-1}}{n^{s}}\right]_{s=1}&=&-\frac12\ln^22+\gamma\ln2 \end{eqnarray}
が知られているので,
\begin{align} \int_0^\infty\frac{x\ln x}{\cosh x+1}dx=2\ln2-\ln^22 \end{align}
がわかりました.

\begin{eqnarray} \int_{-\infty}^{\infty}\binom{n}{x}\binom{m}{x}\binom{n+m+x}{x}dx&=&\int_{-\infty}^{\infty}\frac{n!}{x!(n-x)!}\frac{m!}{x!(m-x)!}\frac{(n+m+x)!}{x!(n+m)!}dx\\ &=&\frac{n!m!}{(n+m)!}\int_{-\infty}^{\infty}\frac{\Gamma(n+m+x)}{\Gamma(x+1)}\frac{1}{\Gamma(x+1)\Gamma(n-x+1)}\frac{1}{\Gamma(x+1)\Gamma(m-x+1)}dx\\ &=&\frac{n!m!}{(n+m)!}\int_{-\infty}^{\infty}\frac{\sin^2\pi x}{\pi^2x^2}\frac{\prod_{k=1}^{n+m}(k+x)}{\prod_{k=1}^{n}(k-x)\prod_{k=1}^{m}(k-x)}dx\\ &=&\frac{1}{2\pi^2}\frac{n!m!}{(n+m)!}\int_{-\infty}^{\infty}\frac{1-\cos(2\pi x)}{x^2}\frac{\prod_{k=1}^{n+m}(k+x)}{\prod_{k=1}^{n}(k-x)\prod_{k=1}^{m}(k-x)}dx \end{eqnarray}
ここで,次の関数の複素積分を考えます.
\begin{align} f(z):=\frac{1-e^{2\pi iz}}{z^2}\frac{\prod_{k=1}^{n+m}(k+z)}{\prod_{k=1}^n(k-z)\prod_{k=1}^{m}(k-z)} \end{align}
積分経路は実軸を$z=l-1\ (l\in\mathbb{N}_{\leq\max(n,m)+1})$の点を微小半円を用いて除きながら通り,大半円を通る次の図のような経路$C$とする.

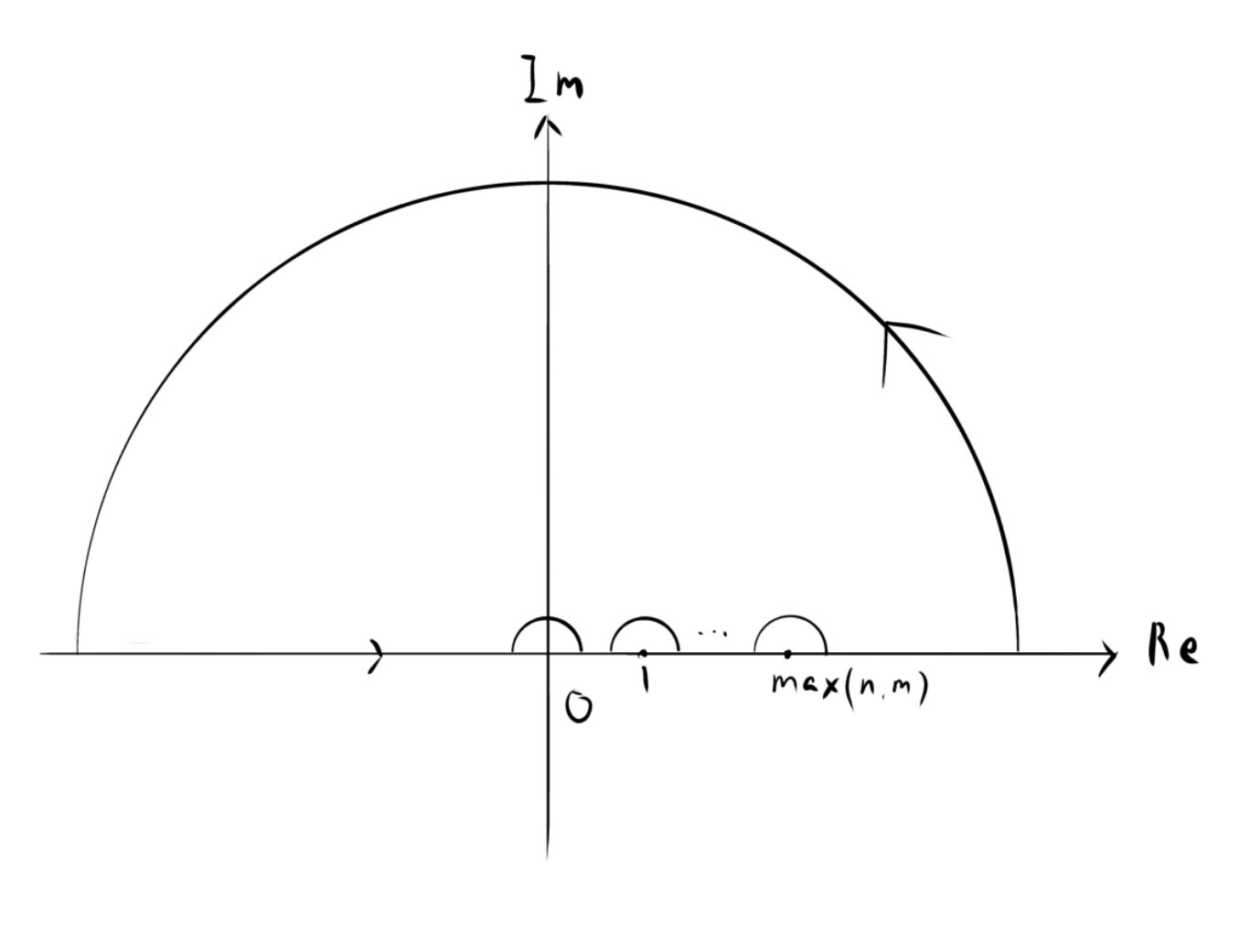
経路$C$内は正則なので次が成り立つ.
\begin{align} \oint_Cf(z)dz=0 \end{align}
そして,十分大きい実数$R$と小さい$\varepsilon$を用いて,
\begin{align} \oint_Cf(z)dz=P.V.\int_{-R}^{R}f(t)dt+\int_0^{\pi}f(Re^{it})Rie^{it}dt-\sum_{k=0}^{\max(n,m)}\int_0^{\pi}f(k+\varepsilon e^{it})\varepsilon ie^{it}dt \end{align}
と書ける.
先ず,
\begin{align} \mathrm{Re}\ P.V.\int_{-R}^{R}f(t)dt=\int_{-\infty}^{\infty}\frac{1-\cos(2\pi x)}{x^2}\frac{\prod_{k=1}^{n+m}(k+x)}{\prod_{k=1}^n(k-x)\prod_{k=1}^m(k-x)}dx \end{align}
なので他の項を計算すれば題意が求まります.
\begin{eqnarray} f(Re^{it})Re^{it}&=&\frac{1-e^{2\pi iR(\cos t+i\sin t)}}{Re^{it}}\frac{O(R^{n+m})}{O(R^n)O(R^m)}\\ &=&\frac{1}{R}O(R^0)(1-e^{2\pi iR\cos t}e^{-2\pi R\sin t}) \end{eqnarray}
より,$t\in(0,\pi)$により
\begin{align} \int_0^{\pi}f(Re^{it})Rie^{it}dt\overset{R\to\infty}{=}0 \end{align}
がわかる.
\begin{eqnarray} \prod_{l=0,l\neq k}^{n}(l-k)&=&(-1)^k\prod_{l=1}^{n-k}l\prod_{l=0}^{k-1}(k-l)\\ &=&(-1)^k(n-k)!k! \end{eqnarray}
なので,$0\leq k\leq\min(n,m)$で,
\begin{eqnarray} \int_0^{\pi}f(k+\varepsilon e^{it})\varepsilon ie^{it}dt&=&i\int_0^{\pi}\frac{1-e^{2\pi i\varepsilon e^{it}}}{\varepsilon e^{it}}\frac{\prod_{l=1}^{n+m}(l+k+\varepsilon e^{it})}{\prod_{l=0,l\neq k}^{n}(l-k-\varepsilon e^{it})\prod_{l=0,l\neq k}^{m}(l-k-\varepsilon e^{it})}dt\\ &\overset{\varepsilon\to0}{=}&i\int_0^{\pi}\frac{1-e^{2\pi i\varepsilon e^{it}}}{\varepsilon e^{it}}\frac{\frac{(n+m+k)!}{k!}}{(n-k)!k!(m-k)!k!}dt\\ &=&\frac{n!}{(n-k)!k!}\frac{m!}{(m-k)!k!}\frac{(n+m+k)!}{k!(n+m)!}\frac{(n+m)!}{n!m!}i\int_0^{\pi}\frac{1-e^{2\pi i\varepsilon e^{it}}}{\varepsilon e^{it}}dt\\ &=&\binom{n}{k}\binom{m}{k}\binom{n+m+k}{k}\frac{(n+m)!}{n!m!}i\int_0^{\pi}\frac{1-e^{2\pi i\varepsilon e^{it}}}{\varepsilon e^{it}}dt\\ &=&''\frac{(n+m)!}{n!m!}i\int_0^{\pi}\left(-2\pi i+O(\varepsilon)\right)dt\\ &=&2\pi^2\frac{(n+m)!}{n!m!}\binom{n}{k}\binom{m}{k}\binom{n+m+k}{k} \end{eqnarray}
$\min(n,m)\lt k\leq\max(n,m)$で,
\begin{eqnarray} \int_0^{\pi}f(k+\varepsilon e^{it})\varepsilon ie^{it}dt&=&i\int_0^{\pi}(1-e^{2\pi i\varepsilon e^{it}})\frac{\prod_{l=1}^{n+m}(l+k+\varepsilon e^{it})}{\prod_{l=0}^{\min(n,m)}(l-k-\varepsilon e^{it})\prod_{l=0,l\neq k}^{\max(n,m)}(l-k-\varepsilon e^{it})}dt\\ &\overset{\varepsilon\to0}{=}&A\int_0^{\pi}1-e^{2\pi i\varepsilon e^{it}}dt=0 \end{eqnarray}
となる.
以上より,
\begin{eqnarray} P.V.\int_{-\infty}^{\infty}f(t)dt&=&2\pi^2\frac{(n+m)!}{n!m!}\sum_{k=0}^{\min(n,m)}\binom{n}{k}\binom{m}{k}\binom{n+m+k}{k} \end{eqnarray}
\begin{eqnarray} \Rightarrow \int_{-\infty}^{\infty}\frac{1-\cos(2\pi x)}{x^2}\frac{\prod_{k=1}^{n+m}(k+x)}{\prod_{k=1}^{n}(k-x)\prod_{k=1}^{m}(k-x)}dx&=&2\pi^2\frac{n!m!}{(n+m)!}\sum_{k=1}^{\min(n,m)}\binom{n}{k}\binom{m}{k}\binom{n+m+k}{k}\\ \Leftrightarrow\int_{-\infty}^{\infty}\binom{n}{x}\binom{m}{x}\binom{n+m+x}{x}dx&=&\sum_{k=0}^{\min(n,m)}\binom{n}{k}\binom{m}{k}\binom{n+m+k}{k} \end{eqnarray}
これにより題意が示されました.