ABJ anomaly：ループダイアグラムによる計算 (1/2)

【Notationについて】

• 次の略称を使用します：

  • VS, AVS: ベクトル対称性、軸性ベクトル対称性 (Vector Symmetry, Axial Vector Symmetry)
  • VT, AVT: ベクトル変換、軸性ベクトル変換 (Vector Transformation, Axial Vector Transformation)
  • VC, AVC: ベクトルカレント、軸性ベクトルカレント (Vector Current, Axial Vector Current)

• $\not A:=\gamma^\mu A_\mu$、$\gamma^\mu$はガンマ行列（ちょっとスラッシュがずれていますがご容赦ください）

• $\epsilon_{\mu\nu\alpha\beta}$は4次元の完全反対称テンソル。本記事では$\epsilon_{0123}=+1$であることに注意。

Axial vector currentの非保存とABJ anomaly

U(1)ゲージ場$A_\mu$を背景場とするmassless fermionの系を考えます：
\begin{align} {\cal L}=\bar\psi(i\not\partial+e\not A)\psi \end{align}
ここで$\bar\psi:=\psi^\dagger \gamma^0$です。この系は次の変換に対して不変です：
\begin{align} \begin{cases} \psi\rightarrow e^{i\theta_V}\psi & \text{ベクトル変換（VT）}\\ \psi\rightarrow e^{i\gamma_5\theta_A}\psi & \text{軸性ベクトル変換（AVT）} \end{cases} \end{align}
これらの変換に対してネーターカレントを計算すると
\begin{align} \begin{cases} j^\mu=i\bar\psi \gamma^\mu\psi & \text{ベクトルカレント（VC）}\\ j^\mu_5=i\bar\psi \gamma_5\gamma^\mu\psi & \text{軸性ベクトルカレント（AVC）} \end{cases} \end{align}
となります。これらの発散は運動方程式を使うことによりゼロであることがわかります:
\begin{align} \begin{cases} \partial_\mu j^\mu=0,\\ \partial_\mu j^\mu_5=0 \end{cases} \end{align}
この保存則は古典的には正しいです。しかし量子論ではAVTに対する対称性が破れ、AVCの発散がノンゼロになります。一方VTの対称性は破れず（というか破れないようにします）、VCの発散は量子論でもゼロです。これをABJ anomalyと呼び、以前記事で議論しました: 「無限ホテル」から始める量子異常 。この記事ではDirac方程式を考え、電場・磁場が一様に存在する場合を考察し、粒子数の定義およびDiracの海の底がないことから、軸性ベクトル対称性（AVS）が破れることを議論しました。

本記事では場の量子論のループダイアグラムの計算により、同様AVSが破れることを見ます。このような計算では正則化を指定する必要がありますが、ここでは球対称な運動量カットオフを使って計算します。もうひとつ次元正則化の方法でも計算できますが、それはまた別記事で書こうと思います。

本記事はRef.ref1に基づいています。また場の量子論の基礎的な事項の説明は省きます。計算に馴染みのない方は、考察対象とする行列要素やダイアグラム、ループ積分はそういうものだと思って受け入れてください。多少参考になりそうな場の量子論関連の記事を以下に載せておきます。

• ネーターカレントの導出・Gell-Mann-Levyの方法
• 走る結合定数の計算(1/5): くりこみ概論
• 走る結合定数の計算(3/5): 摂動計算に関する数学公式集

計算するダイアグラム

次の量を計算します：
\begin{align} \begin{cases} \displaystyle T_{\mu\nu\lambda}(k_1,k_2,q) &:=i\int d^4 x_1 d^4 x_2 \langle 0| T(V_\mu(x_1)V_\nu(x_2)A_\lambda(0))|0\rangle e^{ik_1 x_1+ik_2 x_2},\\ \displaystyle T_{\mu\nu}(k_1,k_2,q) &:=i\int d^4 x_1 d^4 x_2 \langle 0| T(V_\mu(x_1)V_\nu(x_2)P(0))|0\rangle e^{ik_1 x_1+ik_2 x_2} \end{cases} \end{align}
ここで
\begin{align} \begin{cases} V_\mu(x)&=\bar\psi(x)\gamma_\mu \psi(x),\\ A_\mu(x)&=\bar\psi(x)\gamma_\mu \gamma_5\psi(x),\\ P(x)&=\bar\psi(x)\gamma_5\psi(x) \end{cases} \end{align}
です。古典的なカレントの保存則
\begin{align} \begin{cases} \partial^\mu V_\mu(x)&=0,\\ \partial^\mu A_\mu(x)&=2imP(x) \end{cases} \end{align}
および$T$積の微分が
\begin{align} \partial_x^\mu(T(J_\mu(x){\cal O}(y)))= T(\partial^\mu J_\mu(x){\cal O}(y)) +[J_0(x),{\cal O}(y)]\delta(x_0-y_0) \end{align}
であること（T積は階段関数を含み、これを微分した部分からデルタ関数が現れる）、さらに$[V_0(x),A_0(y)]\delta(x_0-y_0)=0$
より、Ward恒等式
\begin{align} k_1^\mu T_{\mu\nu\lambda}&=k^\mu_2T_{\mu\nu\lambda}=0,\\ q^\lambda T_{\mu\nu\lambda}&=2mT_{\mu\nu} \tag{1} \end{align}
を得ます。特に$m=0$の場合、AVCも保存します($q^\lambda T_{\mu\nu\lambda}=0$)。

これをファインマン・ダイアグラムの計算の観点から議論します。対応する最低次のダイアグラムは以下です：

$T_{\mu\nu\lambda}$のダイアグラム

$T_{\mu\nu}$のダイアグラム

これらダイアグラムに対応する式は以下です：
\begin{align} T_{\nu\nu\lambda}&=i\int\frac{d^4p}{(2\pi)^4}(-1) \Bigg\{ {\rm tr}\left[ \frac{i}{\not p-m}\gamma_\mu\gamma_5 \frac{i}{(\not p-\not q)-m}\gamma_\nu \frac{i}{(\not p-\not k_1)-m}\gamma_\mu\right]+(k_1\leftrightarrow k_2, \mu\leftrightarrow \nu) \Bigg\},\\ T_{\nu\nu}&=i\int\frac{d^4p}{(2\pi)^4}(-1) \Bigg\{ {\rm tr}\left[ \frac{i}{\not p-m}\gamma_5 \frac{i}{(\not p-\not q)-m}\gamma_\nu \frac{i}{(\not p-\not k_1)-m}\gamma_\mu\right]+(k_1\leftrightarrow k_2, \mu\leftrightarrow \nu) \Bigg\} \end{align}

ここで$\not q\gamma_5=\gamma_5(\not p-\not q-m)+(\not p -m)\gamma_5+2m\gamma_5$を用いると、$q^\lambda T_{\mu\nu\lambda}$は以下のようになります：
\begin{align} q^\lambda T_{\mu\nu\lambda}&=2mT_{\mu\nu}+\Delta^{(1)}_{\mu\nu}+\Delta^{(2)}_{\mu\nu},\\ \Delta^{(1)}_{\mu\nu} &=\int\frac{d^4p}{(2\pi)^4} {\rm tr}\Bigg[ \frac{i}{\not p-m}\gamma_5\gamma_\nu \frac{i}{(\not p-\not k_1)-m}\gamma_\mu- \frac{i}{(\not p-\not k_2)-m}\gamma_5\gamma_\nu \frac{i}{(\not p-\not q)-m}\gamma_\mu \Bigg],\\ \Delta^{(2)}_{\mu\nu} &=\int\frac{d^4p}{(2\pi)^4} {\rm tr}\Bigg[ \frac{i}{\not p-m}\gamma_5\gamma_\mu \frac{i}{(\not p-\not k_2)-m}\gamma_\nu- \frac{i}{(\not p-\not k_1)-m}\gamma_5\gamma_\mu \frac{i}{(\not p-\not q)-m}\gamma_\nu \Bigg] \end{align}
ここで$\Delta^{(1)}_{\mu\nu},\Delta^{(2)}_{\mu\nu}$の第２項において、それぞれ変数変換$p\rightarrow p+k_2,p\rightarrow p+k_1$を施せばどちらも第１項の積分に一致するので、一見これらは消えるように思えます。消えればAVCは保存されることになります。

しかしこれらのループ積分は線形発散をもち、そのため計算に不定性があります。単純な例として
\begin{align} \int^\infty_{-\infty} [(x+a)-x]dx \end{align}
を考えると、初項の$(x+a)$において変数変換$x\rightarrow x-a$をすればゼロに思えますが、しかし$(x+a)$の$x$と最後の$-x$を先に打ち消せば$\int^\infty_{-\infty} a dx=[ax]^\infty_{-\infty}$になります。当然ですが、このような積分に意味を与えるためには、無限大や不定性の正則化の方法を指定しなければいけません。上のループ積分にはこのような不定性が存在します。

これは場の量子論の致命的な問題点にも思えます。しかしこの不定性の存在が、むしろ現実に起こる現象 -中性パイオンの崩壊- を説明します。

以下ループの正則化を指定し有限化することで、AVCの保存則が破れることを見ます。

球対称な運動量カットオフ

次の積分を考えます：
\begin{align} \Delta a := \lim_{R\rightarrow \infty} \int_{-R}^R [f(x+a)-f(x)] dx \end{align}
$x\gg a$の領域を考え、被積分関数を$x$のまわりでテイラー展開します：
\begin{align} \Delta (a) := \lim_{R\rightarrow \infty} \int_{-R}^R [af'(x)+\frac{1}{2}a^2f''(x)+\ldots] dx \end{align}
$f$は線形発散をもち、$f$の2階微分以降は収束するとすれば
\begin{align} \Delta(a)=\lim_{R\rightarrow \infty}a[f(R)-f(-R)] \end{align}
任意の$n$次元Euclid空間においてこれに対応する式は、Gauss lawを用いて
\begin{align} \Delta(a)&=\lim_{R\rightarrow \infty} i\int_V d^n r [a^\tau \partial_\tau f(r)+\ldots]\\ &=\lim_{R\rightarrow \infty} i\vec a\cdot\int_{\partial V} d\vec S f(r)\\ &=\lim_{R\rightarrow \infty}(i\vec a\cdot \hat nf(R)S_n(R))\\ &=\lim_{R\rightarrow \infty} i\vec a\cdot \frac{\vec R}{R}f(R) \frac{2\pi^{n/2}}{\Gamma(n/2)}R^{n-1} \end{align}
$V$は半径$R$の$n$次元球の体積であり、$\partial V$はその表面積です。$S_n(R)$は半径$R$の$n$次元球面の面積です。$i$のファクターはEuclid化からもたらされます。4次元では
\begin{align} \Delta(a)=2i\pi^2a^\mu \lim_{p\rightarrow \infty} R^2 R_\mu f(R) \end{align}
です。$a^\mu$は積分変数のシフトに対応します。

この正則化を採用し、前章のループ積分を計算します。あとで述べますが、$a$はベクトル対称性（VS）を保存するように決定します。

ループ積分によるanomalyの計算には、この方法の他にも次元正則化に基づく方法があります。本記事の方法の利点は、ループ積分を実行する必要がないことです。上記正則化に対し有限で残る項を被積分関数からとりだし、極限をとればよいです。

ループ積分の計算

次の量を導入します：
\begin{align} T_{\mu\nu\lambda}(a):= (-1)\int\frac{d^4p}{(2\pi)^4} \Bigg\{ {\rm tr}\left[ \frac{i}{(\not p+\not a)+-m}\gamma_\mu\gamma_5 \frac{i}{(\not p+\not a-\not q)-m}\gamma_\nu \frac{i}{(\not p+\not a-\not k_1)-m}\gamma_\mu\right] \\+(k_1\leftrightarrow k_2,\mu\leftrightarrow\nu) \Bigg\} \end{align}
これは$T_{\mu\nu\lambda}$の被積分関数の積分変数を$p\rightarrow p+a$としたものです。この積分に前章の正則化を施すため、次の量を考えます：
\begin{align} \Delta_{\mu\nu\lambda}(a) &:=T_{\nu\nu\lambda}(a)-T_{\nu\nu\lambda}(0)\\ &=\Delta_{\mu\nu\lambda}^{(1)}+\Delta_{\mu\nu\lambda}^{(2)},\\ \Delta_{\mu\nu\lambda}^{(1)} &:=(-1)\int\frac{d^4p}{(2\pi)^4} \Bigg\{{\rm tr}\left[ \frac{i}{(\not p+\not a)-m}\gamma_\mu\gamma_5 \frac{i}{((\not p+\not a)-\not q)-m}\gamma_\nu \frac{i}{((\not p+\not a)-\not k_1)-m}\gamma_\mu\right]\\ &\hspace{3.5cm}-{\rm tr}\left[ \frac{i}{\not p-m}\gamma_\mu\gamma_5 \frac{i}{(\not p-\not q)-m}\gamma_\nu \frac{i}{(\not p-\not k_1)-m}\gamma_\mu\right]\Bigg\}\\ \Delta_{\mu\nu\lambda}^{(2)} &:=(-1)\int\frac{d^4p}{(2\pi)^4} \Bigg\{{\rm tr}\left[ \frac{i}{(\not p+\not a)-m}\gamma_\nu\gamma_5 \frac{i}{((\not p+\not a)-\not q)-m}\gamma_\mu \frac{i}{((\not p+\not a)-\not k_2)-m}\gamma_\nu\right]\\ &\hspace{3.5cm}-{\rm tr}\left[ \frac{i}{\not p-m}\gamma_\nu\gamma_5 \frac{i}{(\not p-\not q)-m}\gamma_\mu \frac{i}{(\not p-\not k_2)-m}\gamma_\mu\right]\Bigg\} \end{align}
前章の正則化より、線形発散の部分のみ取り出します：
\begin{align} \Delta_{\mu\nu\lambda}^{(1)} &=(-1)\int\frac{d^4p}{(2\pi)^4} a^\tau\frac{\partial}{\partial p^\tau} {\rm tr} \left[ \frac{1}{\not p-m}\gamma_\lambda\gamma_5 \frac{1}{(\not p-\not q)-m} \gamma_\nu \frac{1}{(\not p-\not k_1)-m} \gamma_\mu \right]\\ &\xrightarrow{\rm Euclid化}(-1)i\int\frac{d^4p}{(2\pi)^4} a^\tau\frac{\partial}{\partial p^\tau} {\rm tr} \left[ \frac{1}{\not p+m}\gamma_\lambda\gamma_5 \frac{1}{(\not p+\not q)-m} \gamma_\nu \frac{1}{(\not p+\not k_1)-m} \gamma_\mu \right]\\ &\xrightarrow{\rm regularization}2i\pi^2a^\tau \lim_{p\rightarrow\infty} p^2p_\tau \left\{ -\frac{1}{(2\pi)^4}{\rm tr} \left[ \frac{1}{\not p+m}\gamma_\lambda\gamma_5 \frac{1}{(\not p-\not q)+m} \gamma_\nu \frac{1}{(\not p-\not k_1)+m} \gamma_\mu \right] \right\}\\ &=-\frac{1}{(2\pi)^4} 2i\pi^2a^\tau\lim_{p\rightarrow\infty} p^2p_\tau \frac{1}{p^6} {\rm tr} (\gamma_\alpha\gamma_\lambda\gamma_5\gamma_\beta\gamma_\nu\gamma_\delta\gamma_\mu)p^\alpha p^\beta p^\delta\tag{2} \end{align}
ここで
\begin{align} {\rm tr}(\gamma_\mu\gamma_\nu\gamma_\rho\gamma_\sigma\gamma_\alpha\gamma_\beta\gamma^5)&=-4i( \delta_{\mu\nu}\epsilon_{\rho\sigma\alpha\beta} -\delta_{\mu\rho}\epsilon_{\nu\sigma\alpha\beta} +\delta_{\rho\nu}\epsilon_{\mu\sigma\alpha\beta} -\delta_{\alpha\beta}\epsilon_{\sigma\mu\nu\rho} +\delta_{\sigma\beta}\epsilon_{\alpha\mu\nu\rho} -\delta_{\sigma\alpha}\epsilon_{\beta\mu\nu\rho})\\ (\epsilon_{0123}&=+1) \end{align}
であり、Eq.(1)のうち残るのは$\alpha,\beta,\delta$のうち2つが$\delta$で縮約されるもののみ（そのほかは$\epsilon$テンソルと$p$2つの縮約によりゼロ）。よって${\rm tr}$の部分で残るのは$4i\delta_{\alpha\beta}\epsilon_{\lambda\nu\delta\mu}$のみ。ゆえに
\begin{align} {\rm Eq.(1)}=-\frac{1}{(2\pi)^4}2i\pi^2a^\tau \lim_{p\rightarrow \infty} p^2p_\tau\frac{1}{p^6}4i\delta_{\alpha\beta}\epsilon_{\lambda\nu\delta\mu} p^\alpha p^\beta p^\delta \end{align}
です。運動量は球対称に極限をとり
\begin{align} \lim_{p\rightarrow\infty}\frac{p^\tau p^\delta}{p^2}=\delta^{\tau\delta}/4 \end{align}
とします。最終的に
\begin{align} \Delta_{\mu\nu\lambda}^{(1)}=-\frac{1}{8\pi^2}a^\tau\epsilon_{\tau\mu\nu\lambda} \end{align}
となります。

ここで$a^\tau$を
\begin{align} a^\tau=\alpha k_1^\tau+(\alpha-\beta)k^\tau_2 \end{align}
のようにパラメトライズします。$\Delta_{\mu\nu\lambda}^{(2)}$は$\Delta_{\mu\nu\lambda}^{(1)}$で$k_1\leftrightarrow k_2,\mu\leftrightarrow \nu$としたものなので、結局
\begin{align} \Delta_{\mu\nu\lambda}(a)=\Delta_{\mu\nu\lambda}^{(1)}(a)+\Delta_{\mu\nu\lambda}^{(2)}(a)=\frac{1}{8\pi^2}\beta(k_1-k_2)^\rho \epsilon_{\rho\mu\nu\lambda} \end{align}
を得ます。$\Delta_{\mu\nu\lambda}(a)=T_{\mu\nu\lambda}(a)-T_{\mu\nu\lambda}(0)$であったから、
\begin{align} T_{\mu\nu\lambda}(a)=T_{\mu\nu\lambda}(0) -\frac{1}{8\pi^2}\beta(k_1-k_2)^\rho\epsilon_{\mu\nu\lambda\rho}\tag{3} \end{align}
となります。

Axial vector currentの発散に関して

「計算するダイアグラム」の章で書いたように
\begin{align} q^\lambda T_{\mu\nu\lambda}&=2mT_{\mu\nu} +\Delta_{\mu\nu}^{(1)}+\Delta_{\mu\nu}^{(2)},\\ \Delta^{(1)}_{\mu\nu} &=\int\frac{d^4p}{(2\pi)^4} {\rm tr}\Bigg[ \frac{i}{\not p-m}\gamma_5\gamma_\nu \frac{i}{(\not p-\not k_1)-m}\gamma_\mu- \frac{i}{(\not p-\not k_2)-m}\gamma_5\gamma_\nu \frac{i}{(\not p-\not q)-m}\gamma_\mu \Bigg],\\ \Delta^{(2)}_{\mu\nu} &=\int\frac{d^4p}{(2\pi)^4} {\rm tr}\Bigg[ \frac{i}{\not p-m}\gamma_5\gamma_\mu \frac{i}{(\not p-\not k_2)-m}\gamma_\nu- \frac{i}{(\not p-\not k_1)-m}\gamma_5\gamma_\mu \frac{i}{(\not p-\not q)-m}\gamma_\nu \Bigg] \end{align}
です。前章と同様に$\Delta_{\mu\nu}^{(1)},\Delta_{\mu\nu}^{(2)}$に正則化を施し計算します：
\begin{align} \Delta^{(1)}_{\mu\nu} &=\int\frac{d^4p}{(2\pi)^4} {\rm tr}\Bigg[ \frac{i}{\not p-m}\gamma_5\gamma_\nu \frac{i}{(\not p-\not k_1)-m}\gamma_\mu- \frac{i}{(\not p-\not k_2)-m}\gamma_5\gamma_\nu \frac{i}{(\not p-\not q)-m}\gamma_\mu\Bigg]\\ &=-k_2^\tau\int\frac{d^4p}{(2\pi)^4} \frac{\partial}{\partial p^\tau}{\rm tr} \left[ \frac{\not p+m}{p^2-m^2}\gamma_5\gamma_\nu \frac{(\not p-\not k_1)+m}{(p-k_1)^2-m^2}\gamma_\mu \right]\\ &\xrightarrow{\text{Euclid化, regularization}} -\frac{k_2^\tau}{(2\pi)^4}(2i\pi^2)\lim_{p\rightarrow \infty} \frac{p_\tau}{p^2}{\rm tr}(\gamma_\alpha\gamma_5\gamma_\nu\gamma_\beta\gamma_\mu)p^\alpha k_1^\beta \end{align}
ここでtrの中の分子の$p^2$の項はtrで消えることに注意。計算をすすめると
\begin{align} &=-\frac{k_2^\tau}{(2\pi)^4}(2i\pi^2)4i\epsilon_{\alpha\nu\beta\mu} \lim_{p\rightarrow \infty}\frac{p_\tau p^\alpha}{p^2}k_1^\beta\\ &=-\frac{k_2^\alpha}{(2\pi)^4}(2i\pi^2)i\epsilon_{\alpha\nu\beta\mu}k_1^\beta\\ &=-\frac{1}{8\pi^2}\epsilon_{\mu\nu\sigma\rho}k_1^\sigma k_2^\rho \end{align}
となります。ゆえに
\begin{align} q^\lambda T_{\mu\nu\lambda}=2mT_{\mu\nu} -\frac{1}{4\pi^2}\epsilon_{\mu\nu\sigma\rho}k_1^\sigma k_2^\rho \tag{4} \end{align}
を得ます。

一方、Eq.(2)において両辺に$q^\lambda=k_1^\lambda+k_2^\lambda$をかけると
\begin{align} q^\lambda T_{\mu\nu\lambda}(a=\alpha k_1+(\alpha-\beta)k_2) &=q^\lambda T_{\mu\nu\lambda} -\frac{\beta}{8\pi^2}(k_1+k_2)^\lambda\epsilon_{\mu\nu\lambda\rho}(k_1-k_2)^\rho\\ \leftrightarrow q^\lambda T_{\mu\nu\lambda}(a=\alpha k_1+(\alpha-\beta)k_2) &=q^\lambda T_{\mu\nu\lambda}+\frac{\beta}{4\pi^2} \epsilon_{\mu\nu\sigma\rho}k_1^\sigma k_2^\rho \end{align}
ですが、これにEq.(3)を代入して
\begin{align} q^\lambda T_{\mu\nu\lambda}(a=\alpha k_1+(\alpha-\beta)k_2) &=2mT_{\mu\nu}-\frac{1-\beta}{4\pi^2}\epsilon_{\mu\nu\sigma\rho}k^\sigma_1k^\rho_2 \end{align}
を得ます。

Vector currentの発散について

VCの発散については、Eq.(2)より
\begin{align} k_1^\mu T_{\mu\nu\lambda}(a=\alpha k_1+(\alpha-\beta)k_2) =k_1^\mu T_{\mu\nu\lambda}-\frac{\beta}{8\pi^2}\epsilon_{\mu\nu\lambda\rho} (k_1-k_2)^\rho \end{align}
です。$k_1^\mu T_{\mu\nu\lambda}$を計算します：
\begin{align} k_1^\mu T_{\mu\nu\lambda} =(-1)\int\frac{d^4p}{(2\pi)^4} \Bigg\{ {\rm tr}\left[ \frac{1}{\not p-m}\gamma_\lambda \gamma_5\frac{1}{(\not p-\not q)-m} \gamma_\nu\frac{1}{(\not p-\not k_1)-m}\not k_1 \right]\\ +{\rm tr}\left[ \frac{1}{\not p-m}\gamma_\lambda \gamma_5\frac{1}{(\not p-\not q)-m} \not k_1\frac{1}{(\not p-\not k_2)-m}\gamma_\nu \right] \Bigg\} \end{align}
ここで$\not k_1=[(\not p-\not k_2)-m]-[(\not p-\not q)-m]$を用いると
\begin{align} =(-1)\int \frac{d^4p}{(2\pi)^4} {\rm tr} \left[ \gamma_\lambda\gamma_5 \frac{1}{(\not p-\not q)-m}\gamma_\nu\frac{1}{(\not p-\not k_1)-m} -\gamma_\lambda\gamma_5\frac{1}{(\not p-\not k_2)-m}\gamma_\nu \frac{1}{\not p-m} \right] \end{align}
今までと同様Euclid化 & regularizationを施すと
\begin{align} &=\lim_{p\rightarrow \infty}\frac{ik^\tau_1}{(2\pi)^4} \frac{p_\tau}{p}2\pi^2p^3 {\rm tr} \left[ \gamma_\lambda\gamma_5 \frac{-\not k_2}{(p-k_2)^2+m^2}\gamma_\nu \frac{\not p}{p^2+m^2} \right]\\ &=\lim_{p\rightarrow \infty} -k_1^\tau k_2^\alpha \frac{2\pi^2 i}{(2\pi)^4} \frac{p_\tau p^\beta}{p^2} {\rm tr}(\gamma_\lambda \gamma_5 \gamma_\alpha\gamma_\nu\gamma_\beta)\\ &=-\frac{1}{8\pi^2}\epsilon_{\lambda\sigma\nu\rho}k_1^\rho k_2^\sigma \end{align}
ゆえに
\begin{align} k_1^\mu T_{\mu\nu\lambda}=-\frac{1}{8\pi^2}\epsilon_{\lambda\sigma\nu\rho} k_1^\rho k_2^\sigma \end{align}
を得ます。Eq.(2)にこれを代入すれば、VCの発散は
\begin{align} k_1^\mu T_{\mu\nu\lambda}(a=\alpha k_1+(\alpha-\beta)k_2) =\frac{(1+\beta)}{8\pi^2}\epsilon_{\nu\lambda\sigma\rho} k_1^\sigma k_2^\rho \end{align}
となります。

係数の決定

ここまでの結果をまとめると以下のようになります:

どちらも結局$\alpha$には依存せず、自由なパラメータは$\beta$のみです。また$m=0$であっても両方のcurrentを同時に保存させることはできず、必ずどちらかの対称性は破れます。

どちらのカレントを保存させるかというと、VCを保存するようにします。VCの保存則が破れるとgauge symmetryも破れることになります。gauge symmetryの破れはユニタリティの破れ等をもたらし、理論の根本的な整合性を破壊します。よって破るとするならAVCしかありません。本記事では述べませんが、その破れは中性パイオンの崩壊確率を説明し、このようなanomalyが実際に必要であることがわかります。
$\beta=-1$とすればVCの対称性は保たれます。以上から

これは$m=0$におけるaxial Ward identityを次のように変化させます（Appendix 2参照）：

この計算は、以前の記事 「無限ホテル」から始める量子異常 のEq.(3)において$n=4$としたものと一致します（$m=0$とする。$j_5^\mu$と$e^2A^\mu$は同じ量。）。ただし「無限ホテル」の記事では$\epsilon^{0123}=+1$であるのに対し、本記事では$\epsilon^{0123}=-1$で定義しているため、符号が一見違っていることに注意してください。

まとめ

本記事ではABJ anomaly（axial vector symmetryの量子的破れ）をループ積分により導きました。正則化として球対称な運動量カットオフを採用することで、ループ積分の線形発散からもたらされる有限部分を計算しました。正則化における不定なパラメータをvector currentの保存を保つように決定すると、axial vector currentの保存が破れます。その結果は「「無限ホテル」...」の記事の4次元の結果を再現します。

2つほどコメントです：

• ABJ anomalyはfermionの質量には依存しません。
• 上に示したダイアグラム以外アノマリーには寄与しません。これは高次のループは発散の次数が低いためです。

おしまい。${}_\blacksquare$

Appendix 1: QEDのファインマン則

以下本記事で採用しているファインマン則です（Ref.[1]のAppendixより）。

• 運動量保存で制限されない内線の運動量$p$は$\displaystyle\int\frac{d^4p}{(2\pi)^4}$で積分する。
• フェルミオンの閉ループには$(-1)$をかける。
• フェルミオンのプロパゲータとバーテックスに関するファインマン則：
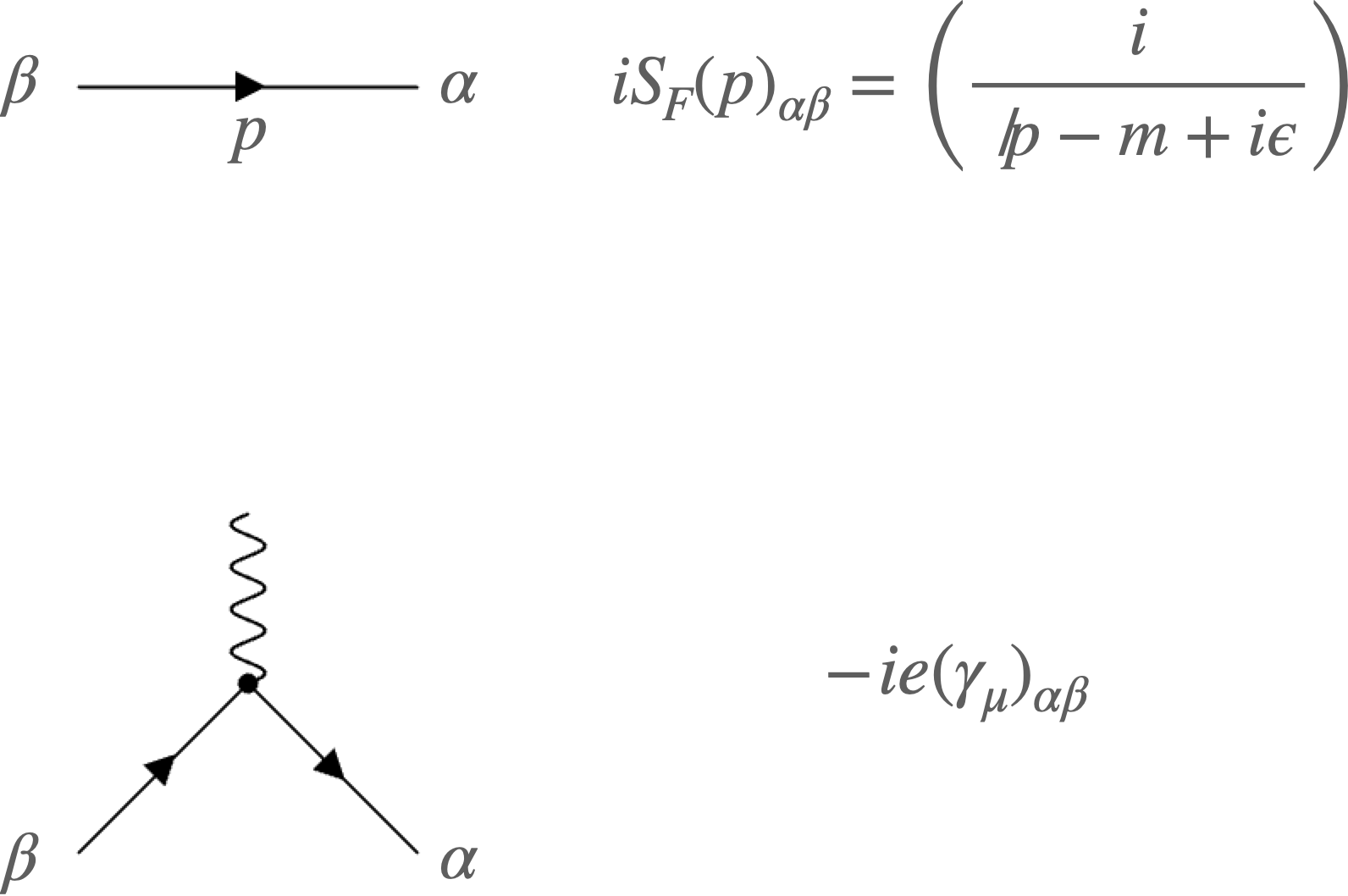  フェルミオンプロパゲータとバーテックスのファインマン則
  ＊光子の伝播関数のファインマン則は本記事では必要ないので割愛しました。

Appendix 2: Eq.(5)の導出

$T_{\mu\nu\rho}$の定義式から始めます：
\begin{align} \int d^4x e^{-iq\cdot x}\langle k_1, k_2|{A_5}_\nu(x)|0\rangle =i(-ie)^2(2\pi)^4\delta^4(k_1+k_2-q) {\epsilon^\lambda}^*(k_1){\epsilon^\mu}^*(k_2) T_{\lambda\mu\nu}(k_1,k_2) \end{align}
左辺の$\langle k_1,k_2|$は運動量$k_1,k_2$の光子の状態、$\epsilon_\mu(p)$は光子$A_\mu(p)$の偏極ベクトルです（偏極ベクトルの基底の足は省略しています）。光子場と区別するため、本文のAVC $A_\mu$を${A_5}_\mu$と書きました。上の式に$iq^\nu$をかけて$q$で積分すれば
\begin{align} \langle k_1, k_2|\partial^\nu {A_5}_\nu(0)|0\rangle =-ie^2{\epsilon^\lambda}^*(k_1){\epsilon^\mu}^*(k_2) iq^\nu T_{\lambda\mu\nu}(k_1,k_2), \ \ \ q_\mu={k_1}_\mu+{k_2}_\mu \end{align}
となります。本文公式2の下の式で$m=0$としたものを$q^\nu T_{\lambda\mu\nu}(k_1,k_2)$に代入すると、上式の右辺は以下のように計算できます：
\begin{align} =-\frac{e^2}{2\pi^2}{\epsilon^\lambda}^*(k_1){\epsilon^\mu}^*(k_2) \epsilon_{\lambda\mu\sigma\rho}k_1^\sigma k_2^\rho \tag{6} \end{align}

次にEq.(5)の右辺の期待値を計算します。
\begin{align} \langle k_1,k_2|\frac{e^2}{(4\pi)^2}\epsilon^{\mu\nu\rho\sigma} F_{\mu\nu}(0)F_{\rho\sigma}(0)|0\rangle =\langle k_1,k_2|\frac{e^2}{(4\pi)^2}4\epsilon^{\mu\nu\rho\sigma} (\partial_\mu A_\nu(0))(\partial_\rho A_\sigma(0))|0\rangle \end{align}
に、$A_\mu$の生成・消滅演算子による展開
\begin{align} A_\mu(x)=\int\frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bf p}}} \sum_{r=0}^3( a^r_{\bf p}\epsilon^r_\mu(p)e^{-ip\cdot x} + {a^r}^\dagger_{\bf p}{\epsilon^r}^*_\mu(p)e^{ip\cdot x}) \end{align}
を代入して計算すると
\begin{align} \langle k_1,k_2|\partial_\mu A_\nu(0)\partial_\rho A_\sigma(0)|0\rangle &= \langle 0|\sqrt{2E_{\bf p}}\sqrt{2E_{\bf k}}a^s_{\bf p}a^t_{\bf k} \int\frac{d^3p'}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bf p'}}} \sum_{r=0}^3( (-ip'_\mu)a^r_{\bf p'}\epsilon^r_\nu(p') + (ip'_\mu){a^r}^\dagger_{\bf p'}{\epsilon^r}^*_\nu(p'))\\ &\hspace{2cm}\times\int\frac{d^3q}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bf q}}} \sum_{u=0}^3( (-iq_\rho)a^u_{\bf q}\epsilon^u_\sigma(q) + (iq_\rho){a^u}^\dagger_{\bf q}{\epsilon^u}^*_\sigma(q))|0\rangle\\ &\hspace{-2cm}= \langle 0|\sqrt{2E_{\bf p}}\sqrt{2E_{\bf k}}a^s_{\bf p}a^t_{\bf k} \int\frac{d^3p'}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bf p'}}} \sum_{r=0}^3( (ip'_\mu){a^r}^\dagger_{\bf p'}{\epsilon^r}^*_\nu(p') \int\frac{d^3q}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bf q}}} \sum_{u=0}^3( (iq_\rho){a^u}^\dagger_{\bf q}{\epsilon^u}^*_\sigma(q)|0\rangle \end{align}
となります。$[a^r_{\bf p},{a^s_{\bf p'}}^\dagger]=(2\pi)^3\delta^{(3)}({\bf p}-{\bf p'})\delta^{rs}$であるから（$r,s$は偏極ベクトルの基底の足）、生成・消滅演算子に関してcontractionをとると
\begin{align} \langle 0|a_{\bf p}^s a_{\bf k}^t {a^r}^\dagger_{\bf p'} {a^u}^\dagger_{\bf q}|0\rangle =(2\pi)^6 (\delta^{(3)}({\bf p}-{\bf p'})\delta^{(3)}({\bf k}-{\bf q})\delta^{sr}\delta^{tu} +\delta^{(3)}({\bf p}-{\bf q})\delta^{(3)}({\bf k}-{\bf p'}) \delta^{su}\delta^{tr}) \end{align}
です。これを用いて計算すれば
\begin{align} \langle k_1,k_2|\partial_\mu A_\nu(0)\partial_\rho A_\sigma(0)|0\rangle= (i{k_1}_\mu){\epsilon^s}_\nu^*(k_1)(i{k_2}_\rho){\epsilon^t}_\sigma^*(k_2) +(i{k_2}_\mu){\epsilon^t}_\nu^*(k_2)(i{k_1}_\rho){\epsilon^s}_\sigma^*(k_1) \end{align}
となります。これに$\epsilon^{\mu\nu\rho\sigma}$をかけると、第１項と第２項は同じ寄与を与えます。以上より
\begin{align} \langle k_1,k_2|\frac{e^2}{(4\pi)^2}\epsilon^{\mu\nu\sigma\rho} F_{\mu\nu} F_{\sigma\rho}(0)|0\rangle&= \langle k_1,k_2|\frac{e^2}{(4\pi)^2}4\epsilon^{\mu\nu\rho\sigma} (\partial_\mu A_\nu(0))(\partial_\rho A_\sigma(0))|0\rangle\\ &=\frac{e^2}{2\pi^2}\epsilon^{\mu\nu\sigma\rho} (i{k_1}_\mu){\epsilon^s}_\nu^*(k_1)(i{k_2}_\sigma){\epsilon^t}_\rho^*(k_2)\\ &= -\frac{e^2}{2\pi^2}\epsilon_{\lambda\mu\sigma\rho} {\epsilon^{\lambda s}}^*(k_1){\epsilon^{\mu t}}^*(k_2) {k_1}^\sigma {k_2}^\rho \end{align}
これはEq.(6)と一致します。よって
\begin{align} \langle k_1, k_2|\partial^\nu {A_5}_\nu(0)|0\rangle =\langle k_1,k_2|\frac{e^2}{(4\pi)^2}\epsilon^{\mu\nu\sigma\rho} F_{\mu\nu} F_{\sigma\rho}(0)|0\rangle \end{align}
が成立します。$\langle k_1,k_2|$, $|0\rangle$を外せばEq.(5)を得ます。${}_\blacksquare$