「無限ホテル」から始める量子異常

はじめに ー無限ホテルは非現実か？ー

「無限ホテルのパラドックス」というお話があります。

無限に部屋が存在するホテルがあります。部屋には端から1,2,...と番号がついています。どの部屋にもお客さんがいるとします。そこにお客さんがもうひとり来ました。部屋は"満室"なのにもかかわらず、このホテルにさらに客を宿泊させることができます。1の部屋の人を2の部屋に、2の部屋の人を3の部屋に、...、iの部屋の人をi+1の部屋に動かせば1の部屋が空くので、そこに新たなお客さんに入ってもらえば良いです（図1）。すべての部屋に宿泊客がいるのに、さらに宿泊客を増やせるというのがパラドックスのように感じます。

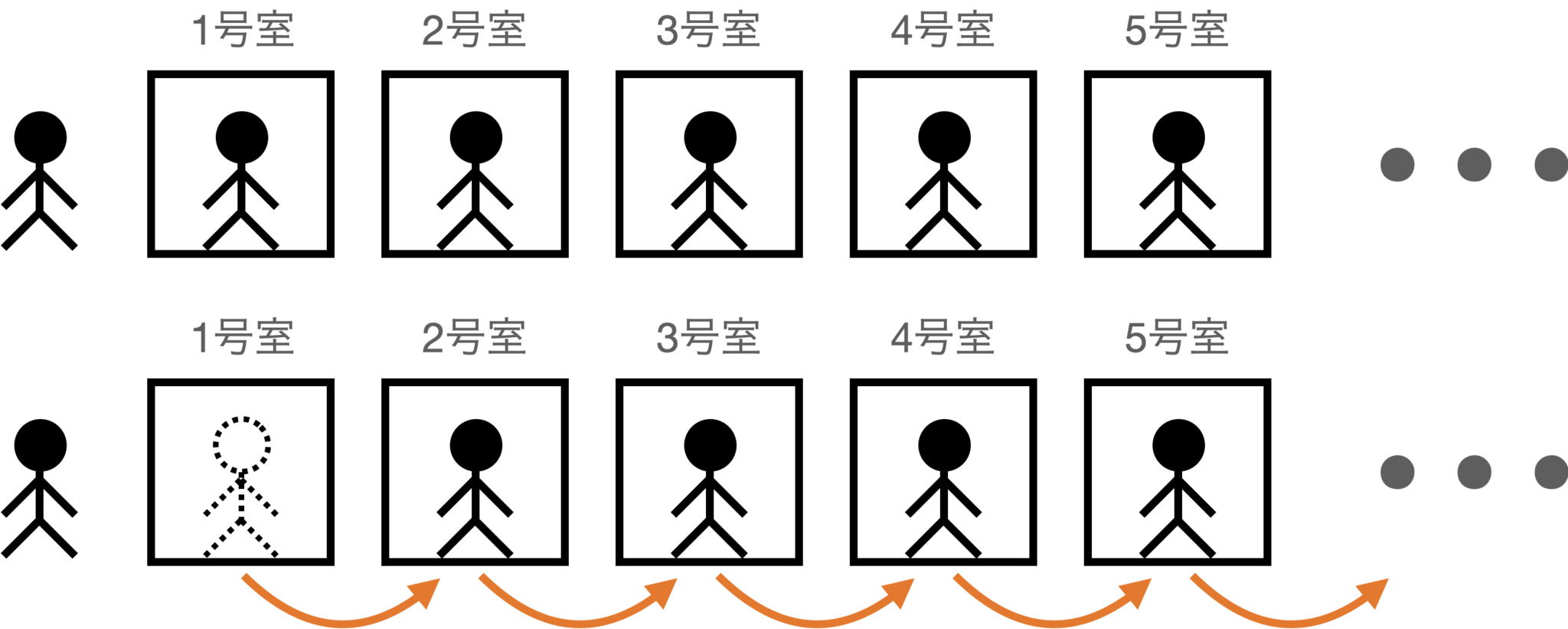無限ホテルの1号室を空ける

このお話は、無限大の集合の要素は数え上げることが不可能であり、一対一対応が可能か否かの比較によってのみ集合の"大きさ"（いわゆる濃度）を測りうることを示しています。無限大という概念がいかに我々の感覚と異なるかを浮き彫りにする例え話です。このような話を聞くと「無限大は実世界には存在しない。単なる数学的な定義の問題であって、現実とは関係ない」と思うのではないでしょうか。

しかし実は無限ホテルに対応する物理 − ABJ anomaly − が存在します。 ABJはこの現象を最初に議論したAdler, Bell, Jackiwの3人の頭文字です。"anomaly"は「異常」という意味の一般名詞ですが、この場合「量子異常」「量子アノマリー」のことを指します。量子異常とは、量子効果により古典的な対称性が破れる現象を表す言葉です。

以下この物理現象に関して述べます。これは量子力学と特殊相対性理論を融合がもたらす"無限"により生じます。そしてこの現象は量子論のトポロジカルな側面と関係します。

本記事はRef.[1]の"The infinite-hotel story"という章およびRef.[2]を元にしています。本記事を読むにはある程度量子力学の知識が必要な部分があります。しかし、ここで言いたいことは難しいことではありません。途中でわけわからなくなったり面倒になったら「ABJ anomalyの無限ホテルによる例え」の章に飛んでください。ここを読むと、この現象と無限ホテルとの対応に関する感覚は理解できるんじゃないかと思います。ポイントはディラックの海には底がないことです。

ディラックの海

ディラックの海（以下Diracの海と表記します）、一度は聞いたことがあるのではないでしょうか。まずこの概念を簡単に説明します。

量子力学ではSchrödinger方程式(SE)

により「状態の時間発展」=「波動関数$\psi$の時間発展」を記述します。しかしこの方程式は、特殊相対論の要請であるローレンツ変換(LT)の下での不変性を持ちません。SEの右辺のハミルトニアンの運動項は$-\frac{1}{2m}\frac{\partial^2}{\partial x^2}$で2階微分である一方、SEの左辺の時間微分は1階微分です。ところがLTは時間と空間を混ぜる変換なので、時間と空間の微分の階数が左辺と右辺で違う方程式はLTで不変にはなりません。

SEをLTの下で不変になるように拡張するのは簡単です。相対論ではエネルギー$E$、運動量$p$、質量$m$の関係は$E^2=p^2+m^2$です。これに対応原理
$$ \quad p\to \frac{1}{i}\frac{\partial}{\partial x}, \ \ \ E\to i\frac{\partial}{\partial t} $$
を入れればKlein-Gordon方程式（KGE）

を得ます。ところがKGEには以下の2つの問題があります。

まず1.について。量子力学では、$|\psi(x,t)|^2$は、時刻$t$において粒子が$x\sim x+dx$の間に存在する確率を表します。これの全空間での積分は、世界のどこかに粒子が存在する確率です。よってこれは時間に依らず$1$になるべきです。ところが上記のKGEの解である$\psi$は、このような時間非依存の規格化が不可能です。よって、$\psi$を粒子の存在確率と結びつけることができません。

1.の問題はDirac方程式（DE）:

で解決されます。$\psi$は$4$成分の波動関数、中括弧は反交換関係:$\{\gamma_\mu,\gamma_\nu\}:=\gamma_\mu\gamma_\nu+\gamma_\nu\gamma_\mu$のことです。$\gamma_\mu$はDirac行列と呼ばれます。これは数学的に言えばClifford algebraの元です。DEはLTの下で共変であり、さらにその解$\psi$は確率解釈が可能です。粒子数の保存、すなわち連続の方程式が成立します。

しかしながら、DEを採用しても2.の問題が残ります。DEの解はエネルギーに関してプラスマイナス対称に存在します。つまり、正のエネルギー$E$の状態に対し、符号を変えた$-E$の状態も必ず存在します。これは不可避な「無限に深い負のエネルギー状態」の存在を意味します。粒子は光を無限に放出し、無限に深いエネルギー状態に落ちこんでいくでしょう。これでは系は不安定になってしまいます。

これを救済するアイディアが「Diracの海」です（図2）。DEによって記述される粒子はフェルミオンと呼ばれ、この粒子は1つのエネルギー準位に1つしか入れません。ならば、負のエネルギー状態はもともと粒子で埋まっている（正確には、粒子の質量を$m$として、$E=-\sqrt{p^2+m^2}|_{p=0}=-m$以下の状態は埋まっている）ことにしてしまえば、負のエネルギーに粒子が落ちることができなくなります。そして、負のエネルギーが埋まった状態が真空であり、それから状態がずれた時のみ観測にかかることにします（図2左図）。負のエネルギー状態を埋めている粒子状態が正エネルギーに励起すると、負のエネルギー状態に穴が空きます。これが（粒子と共に）反粒子として観測されます。いわゆる粒子・反粒子の対生成です（図2右図）。このような前提により相対論的粒子を取り扱う理論は「Diracの空孔理論」と呼ばれます。

Diracの海における粒子描像。●は占有されている状態、○は空いている状態。×は禁制帯。
【左図】 E<0の状態は全て埋まっていて、E>0の状態は全て空いている真空状態。粒子も反粒子も存在しない。
【右図】 E<0におけるある占有状態がE>0に励起した図。E<0に穴が空いた状態が存在し、E>0に占有された状態が存在すると、それらはそれぞれ反粒子と粒子として観測される

これでフェルミオンに関しては1.2.の問題が解決されました。ただ、世の中にはフェルミオンの他にボソンと呼ばれる粒子があります。これは1つのエネルギー準位にいくつでも入れるので、残念ながらDiracの海のアイディアで2.を解決することはできません。その解決は「場の量子論」によりなされます^{${}^{【1】}$}。現在場の量子論は、素粒子を記述する標準的な理論として、また近年では物性系を記述するのにも利用されています。現在では場の量子論はおよそ万人（の物理学者）に受け入れられています。

しかしながら、DEは間違っているわけではありません。例えばDEはSEでは説明できない水素原子のエネルギー準位を再現します。SEと場の量子論の間に、 DEが有効な記述を与えるエネルギー領域が存在します。

本記事では、場の量子論に踏み込むことなく、無限ホテルに対応する物理であるABJ anomalyの概要を説明します。後述しますが、ABJ anomalyの本質はDirac作用素のゼロモードに関連しているので、そういう意味ではDEの考察で十分なのです。

ABJ anomaly

以下「無限ホテル」との対応を簡単かつ明確にするため、$1+1$次元（空間$1$次元、時間$1$次元のこと）における質量ゼロの粒子に対するDEを考えます:
\begin{align} \quad i\gamma^\mu\partial_\mu \psi(x)=0 \end{align}
ここで$\mu=0,1$であり、0成分が時間、1成分が空間成分です。これに伴い$\psi$も$2$成分になります。質量がゼロの粒子を考えるのは以下の議論に本質的です。質量ゼロ、スピン1/2の粒子を「Weyl粒子」と呼びます。

Weyl表現:$\gamma^0=\sigma_x,\gamma^1=i\sigma_y,\gamma^5=\gamma_0\gamma^1=-\sigma_z$を採用し、$\psi_R:=\frac{1+\gamma_5}{2}\psi, \ \psi_L:=\frac{1-\gamma_5}{2}\psi$としてDirac方程式を書き下すと
\begin{align} \quad \begin{cases} i\partial_0\psi_R&=-i\partial_1\psi_R,\\ i\partial_0\psi_L&=i\partial_1\psi_L \end{cases} \end{align}
となります。これをみると$\psi_R$と$\psi_L$が分離しています。モードが分離していると、それらがお互い入れ替わることもなく、粒子数はそれぞれ保存します。以下$\psi_R$のモードをRight Handed (RH)、$\psi_L$のモードをLeft Handed （LH）と呼ぶことにします。RHの粒子数を$Q_R$、LHの粒子数を$Q_L$、全粒子数を$Q:=Q_R+Q_L$(ベクトル電荷)、RHとLHの粒子数の差を$Q_5:=Q_R-Q_L$(軸性ベクトル電荷)とします。
$\psi_{R,L}$で$Q_R,Q_L$を表すと
\begin{align} \quad \begin{cases} \displaystyle Q_R=\int dx^1\langle\psi_R^\dagger\psi_R\rangle, \\ \displaystyle Q_L=\int dx^1\langle\psi_L^\dagger\psi_L\rangle, \end{cases} \end{align}
となります。$\langle\cdot\rangle:=\langle 0|\cdot|0\rangle$は真空$\langle 0\textbar,|0\rangle$による期待値です。それぞれ数が保存するので
\begin{align} \quad \dot Q=\dot Q_R + \dot Q_L=0, \ \ \ \dot Q_5=\dot Q_R-\dot Q_L=0 \end{align}
が成り立ちます。ここでドットは時間微分を表します。
$\psi_R,\psi_L$のdispersion(エネルギー$\omega$と運動量$p$の関係)は、波動関数が$\exp(-i\omega t+ipx)$に比例するので、これをDEに入れて
\begin{align} \quad \begin{cases} \omega=p & \text{for } \psi_R\\ \omega=-p & \text{for } \psi_L \end{cases} \end{align}
となります。以下で電場を$E$で表すため、ここからはエネルギーを$\omega$で表します。

次に、粒子に電磁場をカップルさせます。このときDEは
\begin{align} \quad i\gamma^\mu D_\mu\psi(x)=0, \ \ D_\mu :=\partial_\mu + ieA_\mu\\ \leftrightarrow \begin{cases} i\partial_0\psi_R=(-i\partial_1-eA^1)\psi_R,\\ i\partial_0\psi_L=(i\partial_1+eA^1)\psi_L \end{cases} \end{align}
となります。ここで$x$のプラス方向に一様な電場をかけます。ただし電場は外場とみなし、粒子からの反作用は考慮しません。$A^0=0$とし、電場を$E=\dot A^1$とします。このとき古典的には
\begin{align} \quad \frac{dp}{dt}=-eF^{01}=+eF_{01}=eE \tag{1} \end{align}
が成立します。すなわち一様電場によって粒子は$x$方向に等加速度運動します。量子論でも事情は変わりません。

電場をかけてもRHとLHは分離しているので、両者の粒子数は変わらないように思います。しかし、Diracの海の描像では状況が違います。

図3はRHとLHの真空状態、図4は電場による状態の変化を示した図です。電場がかかる前は、エネルギーゼロのところまで粒子が占有し、そこから上には粒子がない状態だとします（図3）。電場をかける前の「Diracの海」はこのようなものであり、元々の真空$|0\rangle$は図3で規定されます。難しいことではなく、$\omega>0$に存在する黒丸がRHの粒子の数、$\omega>0$に存在する黒四角がLHの粒子の数と理解すればいいです。つまり元々の状態は$Q_R=Q_L=0$です。

RHとLHの真空状態。縦軸はエネルギー$\omega$、横軸は運動量

ここに電場をかけます（図4）。するとEq.(1)にあるように、RHの粒子は加速され、負のエネルギー状態に存在した粒子が正エネルギーに顔をだしてきます。これは、無限ホテルと同じで、それぞれの部屋にいた粒子達が、より高いエネルギーの部屋に皆同時に上がっていく状況に対応します。正エネルギーに顔をだした粒子は粒子数に正の寄与をします。逆に、LHは正のエネルギー状態に存在した粒子が負エネルギーに沈んでいきます。沈んでいくと、負のエネルギー状態に穴が開きます。これはLHの反粒子の生成に対応し、粒子数に負の寄与をします。

$x^1$のプラス方向に電場が存在する場合のRHとLHの状態の変化

ここで、周期的な世界を考えます。$L$だけ進んだら元の場所に戻る世界、すなわち
\begin{align} \quad \psi(x^1+L)=\psi(x^1) \end{align}
とします。すると（空間部分の波動関数は$e^{ip^1 x^1}$に比例するので）エネルギー状態は$2\pi/L$ごとに1つ存在します。RHのdispersionは$\omega=p$であり、$\dot p=eE$なので、エネルギーは単位時間あたり$eE$増えます。よってDiracの海から顔を出すRHの単位時間あたりの数は
\begin{align} \quad \dot Q_R=eE/(L/2\pi)=\frac{L}{2\pi}eE \end{align}
です。一方LHは$\omega=-p$であり、逆にエネルギーが単位時間あたり$eE$減るので、Diracの海に消えていくLHの単位時間あたりの数は
\begin{align} \quad \dot Q_L-=-\frac{L}{2\pi}eE \end{align}
です。よって

を得ます。

以上行ったことを振り返ります。もともとRHとLHは分離しており、電場もこれらを混ぜることはないので、$Q_R, Q_L$はそれぞれ保存する気がします。これは古典的には正しいです。ところが、相対論的な量子力学に移ったとたん、$Q_R, Q_L$が保存しなくなります。そして結果的に$Q_5$は保存せず、時間依存してしまいました。

Diracの海の描像では、正エネルギーの粒子の数が粒子数に正の寄与をし、負エネルギーに開いた穴は、粒子数に負の寄与をします。さらに、Diracの海に底がないことから、底の影響を考える必要がないのが大切です。仮に、海の負のエネルギー部分のあるところまでしか粒子が埋まっておらず、あるところから下は埋まっていないとします(図5。茶色の線から下は状態が空いているとする)。すると、RHの正エネルギー部分に顔を出した粒子が粒子数に正の寄与をした分、それまで埋まっていた負のエネルギー状態に穴が開き（図５左図の下3つの白丸）、これがRH粒子数に負の寄与を与えるので、結局RHの粒子数$Q_R$は変わりません。LHも事情は同じで、負のエネルギーに落ち込んだ粒子が、それまで埋まっていなかった負エネルギー部分の状態を埋めるため（図５右図の下3つの黒四角）、これがLHの粒子数に正の寄与を与え、結局粒子数$Q_L$は変わりません。以上より仮に底があれば、$Q_5=Q_R-Q_L$も変化しなくなってしまいます。

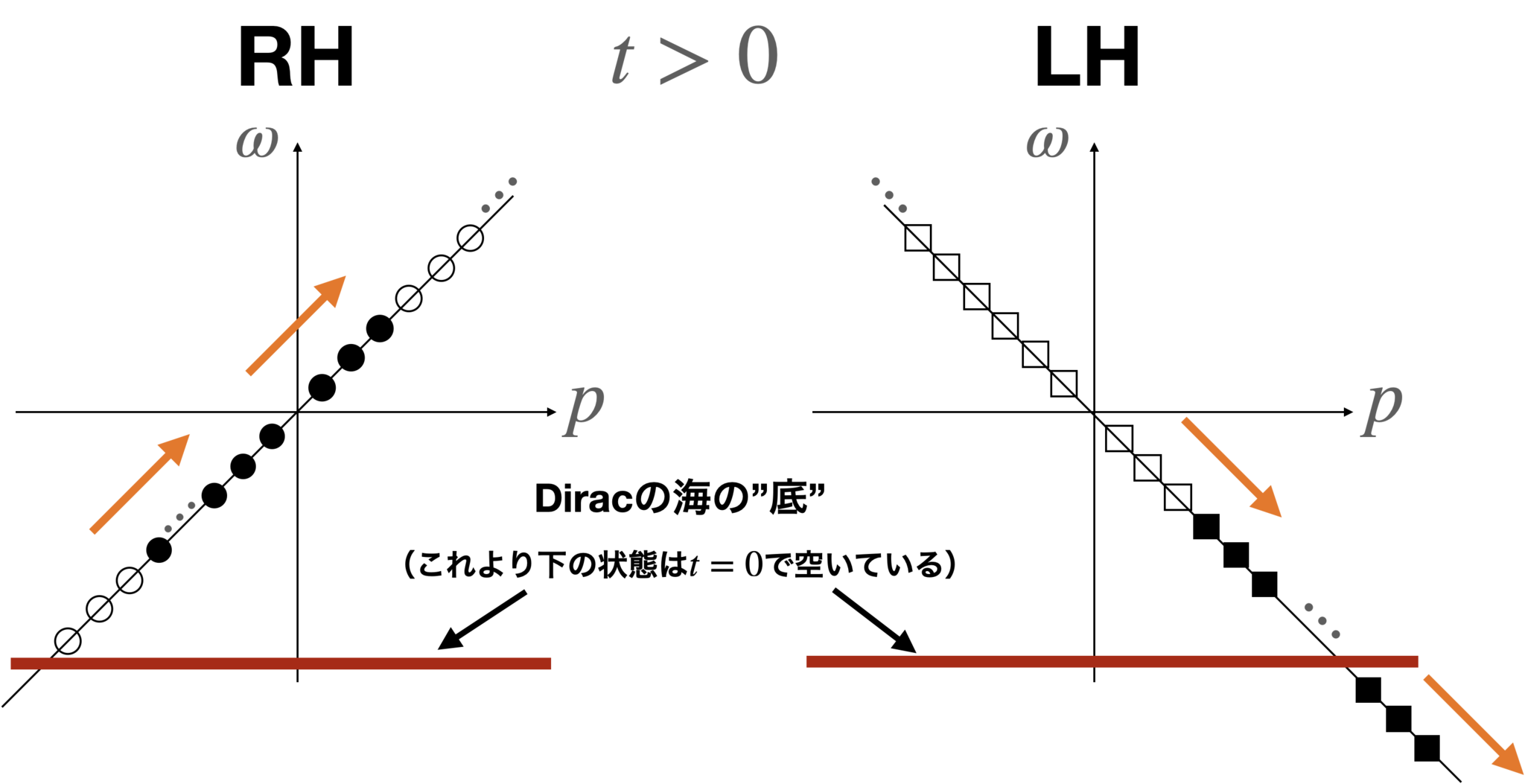Diracの海の"底"の影響（※実際には底は存在しません）。この場合、RHもLHもその粒子数は変化せず、$Q,Q_5$共に変化しない

ABJ anomalyの無限ホテルによる例え

前章の議論を無限ホテルに例えます。
RHの粒子を男性、LHを女性とします^{${}^{【2】}$}。

エネルギー状態の1つ1つはホテルの部屋であり、1室には1人しか泊まれないとします。また、部屋は男性用と女性用にわかれています。エネルギーの大きさは高さに例えます。地上の部屋には、地面に近い方から1,2,3...と番号がつけられています。同様に、地下の部屋には、地面に近い方から-1,-2,-3...と番号がつけられています。

最初（$t=0$）、地下の部屋は、男性用も女性用も満杯だとします（図6）。地上の部屋は、男性用も女性用もぜんぶ空室とします。そして、男性は全員、自分の部屋番号より1つ大きい部屋に、単位時間あたり1回移動します（ただし-1の次は1に移ることにします）。女性は全員、自分の部屋番号より1つ小さい部屋に、単位時間あたり1回移動します（1の次は-1に移ることにします）。

このとき、時刻$t$での男性の人数$N_男(t)$と女性の人数$N_女(t)$がどうなるか考えます。

$t=0$のホテル。男女ともにゼロ人。Diracの海の真空状態に対応。

そもそも$t=0$での$N_男(t=0)$と$N_女(t=0)$はいくつでしょうか。無限人いるから無限大、としてしまうと、状態の変化が起きてもそれを記述できないので避けます。地下の部屋が満杯の状態は、Diracの海でいえば真空状態です。真空状態は粒子が存在しないので、これとのアナロジーで、地下の部屋が満杯かつ地上の部屋がすべて空の状態の人数はゼロと定義しましょう。よって
\begin{align} \quad N_男(t=0)=N_女(t=0)=0 \end{align}
と定義します。

では、$t=0$の状態から人が移動したとき（図7）、人数をどう定義するべきでしょうか。

$t>0$のホテル。男性の地上の部屋は埋まっていき、女性の地下の部屋は空いていく。部屋が埋まった分男性の人数が増え、部屋が空いた分女性の人数が減ると定義する。

ここでは、地面から有限の範囲の部屋だけ考え（無限の底は考慮しない）、$t=0$の状態と比較して部屋が埋まれば埋まった分だけ人数が増加したと定義し、部屋が空けば空いた分だけ人数が減少したと定義します。すると

$\quad N_男(t)=t$       ...地上の部屋が単位時間あたり1つ埋まる
$\quad N_女(t)=-t$     ...地下の部屋が単位時間あたり1つ空く
（ガウス記号をつけるのが正しいのでしょうが、そのへんは適当で）

です。よって全人数を$N_{\rm tot}(t)=N_男(t)+N_女(t)$とし、男女の人数差を$N_{\rm diff}:=N_男(t)-N_女(t)$とします。すると

$\quad N_{\rm tot}(t)=0$     ...全人数は変化しない。男性が増えた分、女性は減っている
$\quad N_{\rm diff}(t)=2t$     ....男性が増え女性は減っているから差は広がる

となります。

これは一見不思議な結果です。男女とも部屋を移っているだけなので、人数は男女ともに変化がなく、$N_{\rm tot}$も$N_{\rm diff}$も時間に依存しない気がします。しかし無限の人数を数えることはできません。そこで、地下の部屋が無限に埋まっている状態を基準にし、その状態をゼロ人と定義しました。そして有限の部屋番号の占有状態の変化にのみ注目し、人数の変化を定義しました。我々人間には、有限部分の変化しか感知できないので、これができることの限界といってもいいかもしれません。いづれにせよ、このように定義すると、人数という概念が無限に煩わされずにwell definedになります。そしてこの影響は、$Q_5$（男女の人数差）の非保存という"異常"を導きます。一方で$Q$（男女の全人数）は保存します。

(3+1)次元のABJ anomaly

次に(3+1)次元のABJ anomalyについて述べます。
この場合重要なのは、電場だけでなく磁場が存在する状況を設定することです。

これに関しては別記事を書きました： (3+1)次元一様磁場中のワイル粒子
ここではこの記事の結果のみ引用します。

(3+1)次元において、$3$方向（$z$方向）に一様磁場$H$をかけます。このときWeyl粒子のエネルギー固有値は以下のようになります：
\begin{align} \quad \omega(n,\sigma^3,p^3)= \pm\sqrt{2eH(n+1/2)+(p^3)^2-eH\mu} \ \ \ (\mu=\pm 1) \end{align}
ここで$\omega$は粒子のエネルギー。$n$は、Landau準位と呼ばれる、粒子のサイクロトロン運動に関するエネルギー準位を指定する整数。$\mu=\pm 1$はスピンと磁場の結合に関する量子数。$p^3$は$z$方向の運動量です（$z$方向には粒子は自由に動けることに注意）。

粒子のdispersionは以下のようにまとめられます：

このdispersion relationを図にしたのが図8です。

z方向に一様な磁場がかかったときの粒子のdispersion relation

これをみると、$\psi_R$は磁場中では1つだけ線形のモード: $\omega=p^3$を持ちます。このモードは(1+1)次元のときと同様、負のエネルギーから正のエネルギーに連続的につながっています。同様に$\psi_L$は1つだけ線形のモード: $\omega=-p^3$を持ちます。真空状態は$\omega\le 0$がすべて占有され、$\omega>0$がすべて空いている状態です。そしてこれら以外正と負のエネルギーをつなぐモードは存在しません。

ここに(1+1)次元の場合と同様電場を3方向（z方向）にかければ、RHの粒子は加速され$p^3$は時刻と共に大きくなり、$\omega\le0$の状態がどんどん正のエネルギー状態に顔をだし、粒子生成が起きます。逆にLHの粒子は時間が経つにつれ$\omega<0$の状態がどんどん空いていき、反粒子生成が起きます。(1+1)次元のときと同様、3方向に周期境界条件を課すと（周期$L$）

\begin{align} \quad \dot Q_R&=\frac{LeH}{4\pi^2}\omega(n=0,\sigma_3=-1,p^3)=\frac{e^2L}{4\pi^2}EH,\\ \dot Q_L&=-\frac{e^2L}{4\pi^2}EH=-\dot{\bar Q_L} \end{align}

となります。よって

です。この場合も$Q_5$は異常な振る舞いを示し、時間とともに値が大きくなります。

ちなみに、電場は断熱的(adiabatic)にかけます。これは、$n\neq 0$の状態（双曲的なdispersionをもつモード）を占有する粒子が正エネルギー状態に現れないように電場をゆっくりかける、ということです。あまり大きな電場を突然かけると、正エネルギーに繋がらない状態も励起されてしまいます。

軸性ベクトルカレントの非保存

(3+1)次元では磁場をかけることで線形のdispersionを持つモードが出現し、そこに電場をかけることがABJ anomalyに重要でした。(3+1)次元で電場と磁場が必要な理由を考えます。

対称性が存在する場合、それに対応するカレントなるものが存在します（ネーターの定理）。$Q$は保存するので対応するカレント（ベクトルカレント）が存在し、付随する対称性（ベクトル対称性）が成立しています。一方、$Q_5$は古典的には保存し量子論では保存しないので、対応するカレントが量子論では保存せず、付随する対称性（軸性ベクトル対称性）も量子効果で破れます。カレント$j_\mu$が保存する場合、その発散$\partial^\mu j_\mu$はゼロになり、保存しない場合はノンゼロになります。

空間$d$次元において$Q_5$に対応するカレント（軸性ベクトルカレント）を$j_{5\mu}(x)$とすると、
\begin{align} \quad Q_5=\int d^dx \ j_{5 0}(x) \end{align}
が成立します。(1+1)次元のとき$\dot Q_5=\frac{L}{\pi}eE$だったので、$j_{5 i}(x)$の空間積分がゼロになるとすると
\begin{align} \quad \dot Q_5=\int dx \ \partial^0j_{50}=\int dx \ \partial^\mu j_{5\mu}\\ =\frac{L}{\pi}eE=-\frac{eL}{2\pi}\epsilon^{\mu\nu}F_{\mu\nu} \end{align}
になります（$\epsilon_{\mu\nu}$は完全反対称テンソル。$\epsilon_{01}=-\epsilon^{01}=1$）。ここで$\dot Q_5$と電場の関係が任意の積分領域で成立すると仮定すれば
\begin{align} \quad \partial^\mu j_{5\mu}=-\frac{e}{2\pi}\epsilon^{\mu\nu}F_{\mu\nu} \end{align}
が成立します。よって発散はゼロではなく、軸性ベクトル対称性が破れていることがわかります。この式から、(3+1)次元の場合の発散は、$\epsilon$を4次元の完全反対称テンソルに変えることで右辺のLorentzの足が4つになり
\begin{align} \quad \partial^\mu j_{5\mu}(x)\propto \epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma} \end{align}
となるのではないかと推察されます。そしてこの推測は正しいです。天下りですが、量子電磁気学（Quantum ElectroDynamics, QED）における軸性ベクトルカレントの発散は一般の$2n$次元において

と書けます(Ref.[3]P667)。そして$\vec H$を磁場とすると
\begin{align} \quad \epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma}\propto \vec E\cdot \vec H \end{align}
なので、(3+1)次元におけるABJ anomalyは電場と磁場の内積に比例します。これが(3+1)次元で電場だけでなく磁場を必要とした原因です。

(3+1)次元において、$A^2=Hx^2$および$A^3=-Et$を、Eq.(3)で$n=2$とした式
\begin{align} \quad \partial^\mu j_{5\mu}=-\frac{e^2}{16\pi^2}\epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma} \end{align}
に代入すると、少しの計算ののち

\begin{align} \quad \dot Q_5&=\int d^3x \partial^0 j_{50}=\int d^3x \partial^\mu j_{5\mu}\\ &=\int d^3x \left(-\frac{e^2}{16\pi^2}(-8EH)\right)=\frac{Le^2}{2\pi^2}EH \end{align}
となり、Eq.(2)の結果を再現します。

指数定理との関係

Eq.(3)で示した式はどのように導かれたのでしょうか。これに関しては後日他の記事で述べますがMathlogFujikawaMathlogZeromode、ここでは概要だけ述べておきます。

改めてABJ anomalyが生じた原因をまとめておきます。$Q_5$の異常な生成は、Dirac方程式の「ゼロモード」、すなわち

$\quad i\gamma^\mu D_\mu\psi_n=\lambda_n\psi_n$のうち$\lambda_n=0$のモード、つまり$i\gamma^\mu D_\mu\psi=0$を満たすモード

の状態占有数のRHとLHの差によるものでした。そしてそれは線形なdispersionのモードにより引き起こされました。(1+1)次元ではそもそも線形なdispersionのモードしかありませんでした。(3+1)次元では、双曲的なdispersionをもつモードと線形なdispersionのモードがありました。しかし、双曲的なモードはRHもLHも同じであり、正負エネルギー間の状態のフローも存在しないため、$Q_5$には影響しませんでした。線形モードのみがRHとLHの差を生じさせ、anomalyに寄与します。

さて、Eq.(3)は場の量子論の計算から導かれます。場の量子論において、ABJ anomalyを直観的に理解するには、経路積分がわかりやすいです（藤川の方法。Ref.[4]MathlogFujikawa）。経路積分形式の場の量子論では、このゼロモードの存在が、軸性ベクトル変換（$Q_5$の保存に関わる変換）に関する非自明なヤコビアンを生みます。このヤコビアンの存在のため、古典的に存在する軸性ベクトル対称性が破れ、量子異常が生じます。ヤコビアンはそのままではwell definedではないので、正則化して計算します。するとヤコビアンはゼロモードのRHとLHの間の占有数の差に等しくなりますMathlogZeromodeMathlogInstanton。 このようにしてEq.(3)が導かれます。Diracの海の描像におけるABJ anomalyは、こうして場の量子論でも同じように現れます。

ABJ anomalyは、RHとLHのゼロモードの差というWeyl粒子の性質、ひいてはDirac作用素の性質が、ゲージ場の性質（$\epsilon^{\mu\nu\rho\sigma...}F_{\mu\nu\rho\sigma...}$）で定まることを主張します。これは指数定理の反映ですMathlogZeromodeMathlogInstanton。ABJ anomalyに関わるのはAtiyah-SingerおよびAtiyah-Patodi-Singerの指数定理です。Atiya-Singerの指数定理をWikipediaから引用すると以下のように書かれています：

スピン${}^c$多様体 の上の複素ベクトル束の間の楕円型微分作用素について、解析的指数と呼ばれる量と位相的指数と呼ばれる量とが等しいという定理である。解析的指数は与えられた楕円型微分作用素が定める偏微分方程式の解の次元を表す解析的な量であり、一方で位相的指数は微分作用素の主表象をもとにして多様体のコホモロジーを通じて定義される幾何的な量である。

上記の楕円型微分作用素は、本記事ではDirac作用素$i\gamma^\mu D_\mu$のことです。指数定理はABJ anomalyの文脈で言えば、この作用素のゼロモード解の性質が、ファイバー束（$\simeq$ゲージ場）で定まる位相不変量で表されるということです。実際Eq.(3)の右辺は$n$次Chern指標と呼ばれる量であり(Ref.[5] P90)、ファイバー束が大域的にどの程度「ねじれているか」あるいは「どの程度非自明か」を測る指標です。

ABJ anomalyだけでなく、一般に、量子アノマリーはゲージ場の大域的な位相構造により決定され、詳細な構造には依存しません。

現実世界のABJ anomaly

ここでABJ anomalyが現実に起きるかについて考えます。

ここまでの議論は真空の話でした。もし世の中に電荷をもつWeyl粒子が存在したら、真空に磁場と電場を並行にかけることで、RHの粒子とLHの反粒子の生成が起きるでしょう。完全に質量ゼロでなくとも、それが非常に軽ければ、粒子の質量に対し非常に強い磁場と電場をかけることで同様の現象は起こるんじゃないかと思います。しかし、最も質量の小さいDirac粒子である電子でさえ、その質量に対し強い電磁場を発生させることは、現在のところ不可能です^{${}^{【3】}$}。

中性パイオンの崩壊

では結局ABJ anomalyは現実では起きないのでしょうか。実はABJ anomalyは中性パイオンの崩壊を説明します。というか、もともとABJ anomalyはこの物理現象に関連して議論されました（Ref.[6][7]MathlogPion）。　

電荷ゼロのパイオンである中性パイオン$\pi^0$は、だいたい$10^{-16}$秒で2つの光子$\gamma\gamma$に崩壊します。ところが、場の量子論でこの崩壊の確率振幅に関するファインマン・ダイアグラムを計算するとゼロになります（サザーランド・フェルトマンの定理）。しかし計算を注意深く行うと、サザーランド・フェルトマンの定理では考慮されていない、発散に伴う不定性があることがわかります。おおざっぱにいえば、計算には線形に発散する量同士の引き算が現れるのですが、これを計算するとき、どのように正則化（=一時的なカットオフを入れること。計算の最後でカットオフは無限大にする）を行うかで、答えが変わります。ではどのような基準に基づき正則化するかというと、ベクトルカレント($Q$に関わるカレント)を保存するようにします。このとき軸性ベクトルカレント（$Q_5$に関わるカレント）の保存則は破れます。そしてこの破れは、上記した中性パイオンの寿命$\sim 10^{-16}$秒を見事に説明します。詳しくはMathlogPionをご参照ください。

中性パイオンに関わる軸性ベクトルカレントの発散は、パイオン質量がゼロの場合

\begin{align} \quad \langle\partial^\mu j^{3}_{5\mu}\rangle =\frac{e^2}{32\pi^2}\epsilon_{\mu\nu\rho\sigma}F^{\mu\nu}F^{\rho\sigma} \end{align}

となります。右辺は$\epsilon FF$の形をしており、ABJ anomalyであることがわかります。$j^3_{5\mu}$の3は、アイソスピンの第３成分の軸性ベクトルカレントであることを指します。アイソスピンの第３成分は中性のパイオンに関わる量です。

上記のファインマン・ダイアグラムの計算は、上記した経路積分の方法（=藤川の方法）と本質的には同じですが、量子異常のトポロジカルな側面を理解するには藤川の方法が優れていますMathlogFujikawa。

線形発散の正則化の方法を指定することは、Diracの海の描像で言えば、ホテルの底をどこか有限の部屋番号でとりあえず切っておき、そこまで考慮して計算し、最後に無限大にもっていくようなことだと思えばいいです。「ABJ anomalyの無限ホテルによる例え」で言えば、男女の人数を

$\quad N_男:=$「$-n$以上$n$以下の部屋番号の部屋のうち埋まっている男性部屋の数」
$\quad N_女:=$「$-n$以上$n$以下の部屋番号の部屋のうち埋まっている女性部屋の数」

と定義し、後で$n\to \infty$としているようなものです。こう定義しておけば、$t$秒後の人数はそれぞれ

となります。 $N_男, N_女, N_{\rm tot}$は$n\to \infty$で無限大になりますが、初期状態において人数$N_男=N_女＝n$がゼロになるように、$N_男、N_女$からそれぞれ$n$をさっぴいて定義しておけばよいです。

物性系におけるABJ anomaly

「実世界のABJ anomaly」としてもうひとつ重要なことに、物性系におけるABJ anomalyの実現があります。これは近年注目を集めている、物性系におけるトポロジーの話題 − Weyl semimetal、Graphene、topological insulator等 − と関係します。これらの系に線形のdispersionのモードが存在することが重要です。Ref.[8]ではこれらの現象にABJ anomalyの観点で言及しています。

これら物性系の話題に関しては、他の記事で改めて書こうと思います。
（31Oct.2022追記: Ref.[10]のレクチャーノートに、物性系における量子アノマリーの入門的内容が網羅的に記載されています）

まとめ

本記事では「無限ホテルのパラドックス」を土台にして、ABJ anomalyについて解説しました。

「質量ゼロのDirac粒子」=「Weyl粒子」が存在する場合、(1+1)次元において真空中に電場をかけると、古典的には生じ得ない$Q_5$（RHとLHの粒子数の差）の生成が起きることを見ました。このように量子論において$Q_5$の保存に関連する対称性が破れることで$Q_5$が生成される現象をABJ anomalyと呼びます。一般に、古典的には成立している対称性が量子論で破れる現象を「量子アノマリー」と呼びます。そしてこの現象にはDiracの海に底が存在しないことは重要でした。

(3+1)次元では電場と磁場の両方が存在する場合に$Q_5$の生成が起きます。これは(3+1)次元では軸性ベクトルカレントの発散が$\epsilon^{\mu\nu\rho\sigma}F_{\mu\nu}F_{\rho\sigma}\propto \vec E\cdot \vec H$に比例することによります。そして(1+1)次元でも(3+1)次元でも、線形のdispersionをもつモードがRHとLHの差を生みました。このように、Dirac作用素のゼロモード（$i\gamma^\mu D_\mu =0$の解）がゲージ場により表現されるのは、指数定理の現れです。一般に量子アノマリーは、系の詳細な状態には依存せず、ゲージ場（ファイバー束）の大域的な位相構造により決定されます。

本記事で記したABJ anomalyは「Atiyah-Patodi-Singerの指数定理」=「境界つき多様体上のAtiyah-Singerの指数定理」と関係します。RHとLHのモードの差は、占有された状態が電場により"流れる"「スペクトルの流れ」で表されました。この事実はもっときちんと数学的に扱うことができます。これに関してはまた記事にします。

もともとABJ anomalyは中性パイオンの崩壊に関係するダイアグラムの計算により発見されました。これに関しては本記事では少し言及するに留めました（11Aug.2023追記:MathlogPionに詳細を書きました）。また物性系とABJ anomalyの関連に関しては殆ど何も話しませんでした。これらに関してもそのうち記事にしたいと思います。

おしまい。${}_\blacksquare$