ラマヌジャン総和法4：応用例
はじめに
この記事では
前回の記事
に引き続きラマヌジャンの総和法について勉強していきます。
今回の記事では
前回の記事
で紹介した定理たちを用いたラマヌジャン和の興味深い応用例について見ていき、このシリーズの最終回としたいと思います。
$\Z$上の総和
$$\sum^\R_{n\in\Z}e^{\a n}=0\quad(0<|\a|<\pi)$$
オイラーは"divergent calculation"として次のような式変形をしていたようです。
$$\sum_{n\in\Z}e^{\a n}=\sum_{n\geq1}e^{\a n}+\sum_{n\geq0}e^{-\a n}=\frac{e^\a}{1-e^\a}+\frac1{1-e^{-\a}}=0$$
しかしこれはラマヌジャン和を用いることで次のように正当化できます。
前々回の記事
の例1として求めたように
$$\sum^\R_{n\geq1}e^{-zn}=\frac{e^{-z}}{1-e^{-z}}-\frac{e^{-z}}z$$
が成り立つので
\begin{align}
\sum^\R_{n\in\Z}e^{\a n}
&=\sum^\R_{n\geq1}e^{\a n}+\sum^\R_{n\geq1}e^{\a(1-n)}-\int^1_0e^{\a x}dx\\
&=\l(\frac{e^\a}{1-e^\a}+\frac{e^\a}\a\r)+\l(\frac{e^{-\a}}{1-e^{-\a}}-\frac{e^{-\a}}\a\r)e^\a-\frac{e^\a-1}\a\\
&=0
\end{align}
を得る。
$$\sum^\R_{n\in\Z}n^k=0\quad(k\geq0)$$
「整数の$k$乗の総和は$0$となる」と言うとそんなわけなさ過ぎて面白いですね。
\begin{align}
\sum^\R_{n\geq1}1&=\frac12\\
\sum^\R_{n\geq1}n^{2k}&=\frac1{2k+1}\\
\sum^\R_{n\geq1}n^{2k-1}&=\frac{1-B_{2k}}{2k}
\end{align}
であったことに注意すると
$$\sum^\R_{n\in\Z}n^k=\sum^\R_{n\geq1}n^k+\sum^\R_{n\geq1}(-n)^k-\int^1_{-1}x^kdx=0$$
を得る。
$$\sum^\R_{n\in\Z}\frac1{z-\pi n}=\cot z$$
通常の部分分数展開
では
$$\cot z=\frac1z+\sum^\infty_{\substack{n=-\infty\\n\neq0}}\l(\frac1{z-\pi n}+\frac1{\pi n}\r)$$
のように収束因子$1/\pi n$が必要でしたがラマヌジャン和ではその必要はありません。
\begin{align}
\sum^\R_{n\geq1}\frac1{z-\pi n}
&=\frac1z+\sum^\R_{n\geq1}\frac1{z-\pi n}+\sum^\R_{n\geq1}\frac1{z+\pi n}-\int^1_{-1}\frac1{z-\pi x}dx\\
&=\frac1z+\sum^\R_{n\geq1}\frac{2z}{z^2-\pi^2n^2}-\int^1_0\frac{2z}{z^2-\pi^2x^2}dx\\
&=\frac1z+\sum^\infty_{n=1}\frac{2z}{z^2-\pi^2n^2}
-\int^\infty_1\frac{2z}{z^2-\pi^2x^2}dx-\int^1_0\frac{2z}{z^2-\pi^2x^2}dx\\
&=\cot z+\l[\frac1\pi\log\frac{z-\pi x}{z+\pi x}\r]^\infty_0\\
&=\cot z
\end{align}
を得る。
部分分数展開と言えばディガンマ関数
$$\psi(z)=\frac{d}{dz}\log\G(z)=-\g-\sum^\infty_{n=0}\l(\frac1{n+z}-\frac1{n+1}\r)$$
に関する次の式も面白いですね。
$$\sum^\R_{n\geq1}\frac1{n+z}=-\psi(z+1)+\log(z+1)$$
\begin{align}
\sum^\R_{n\geq1}\l(\frac1n-\frac1{n+z}\r)
&=\sum^\infty_{n=1}\l(\frac1n-\frac1{n+z}\r)-\int^\infty_1\l(\frac1x-\frac1{x+z}\r)dx\\
\sum^\R_{n\geq1}\frac1n-\sum^\R_{n\geq1}\frac1{n+z}
&=\g+\psi(z+1)-\l[\log\frac x{x+z}\r]^\infty_1\\
\g-\sum^\R_{n\geq1}\frac1{n+z}
&=\g+\psi(z+1)-\log(z+1)\\
\end{align}
とわかる。
倍数公式
$$1+\sum^\infty_{n=1}\frac2{(4n)^3-4n}=\frac32\log2$$
たまには収束級数も求めてみましょう。ちなみにこれはラマヌジャンがインドの数学誌に初めて出題した問題の一つでした。
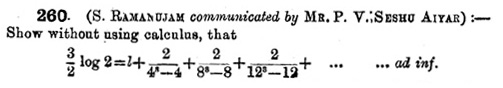Collected Papersより
倍数公式などから
\begin{align}
\sum^\R_{n\geq1}\frac1n
&=\g\\
&=\sum^\R_{n\geq1}\frac1{2n}+\sum^\R_{n\geq1}\frac1{2n-1}-\frac12\int^2_1\frac{dx}x\\
\sum^\R_{n\geq1}\frac1{2n-1}
&=\frac{\g+\log2}2\\
\sum^\R_{n\geq1}\frac1{2n+1}
&=\sum^\R_{n\geq1}\frac1{2n-1}-1+\int^2_1\frac{dx}{2x-1}\\
&=\frac{\g+\log2+\log3}2-1\\
&=\sum^\R_{n\geq1}\frac1{4n+1}+\sum^\R_{n\geq1}\frac1{4n-1}-\frac12\int^2_1\frac{dx}{2x+1}
\end{align}
が成り立つことに注意すると
\begin{align}
\sum^\R_{n\geq1}\frac2{(4n)^3-4n}
&=\sum^\R_{n\geq1}\frac1{2n(4n+1)(4n-1)}\\
&=-\sum^\R_{n\geq}\frac1{2n}+\sum^\R_{n\geq1}\frac1{4n+1}+\sum^\R_{n\geq1}\frac1{4n-1}\\
&=-\frac{\g}2+\frac{\g+\log2+\log3}2-1+\frac{\log5-\log3}4\\
&=-1+\frac12\log2+\frac14\log3+\frac14\log5
\end{align}
がわかる。
また
\begin{align}
\int^\infty_1\frac2{(4x)^4-4x}dx
&=\int^\infty_1\l(-\frac1{2x}+\frac1{4x+1}+\frac1{4x-1}\r)dx\\
&=\l[\frac14\log\frac{(4x)^2-1}{x^2}\r]^\infty_1\\
&=\log2-\frac14\log3-\frac14\log5
\end{align}
が成り立つことに注意すると
\begin{align}
1+\sum^\infty_{n=1}\frac2{(4n)^3-4n}
&=1+\sum^\R_{n\geq1}\frac2{(4n)^3-4n}+\int^\infty_1\frac2{(4x)^4-4x}dx\\
&=\frac32\log2
\end{align}
を得る。
$$\G(Nz)=\frac{N^{Nx-\frac12}}{(2\pi)^{\frac{N-1}2}}\prod^{N-1}_{k=0}\G\l(x+\frac kN\r)$$
$f(x)=\log x$のfractional sumは$\vp(x)=\log\G(x+1)$と求まるので$f(x/N)=\log x-\log N$つまり
$$\vp[f(x/N)](x)=\log\G(x+1)-x\log N$$
が成り立つことおよび
\begin{align}
\sum^\R_{n\geq1}\log n&=\frac12\log2\pi-1\\
\sum^\R_{n\geq1}\log\frac nN
&=\sum^\R_{n\geq1}\log n-\log N\sum^\R_{n\geq1}1\\
&=\frac12\log2\pi-1-\frac12\log N\\
N\int^1_{1/N}\log x\ dx
&=N[x\log x-x]^1_{1/N}\\
&=\log N-(N-1)
\end{align}
に注意すると
$$\log\G(x+1)-x\log N
=\sum^N_{k=1}\log\G\l(\frac{x+k}N\r)
-\frac{N-1}2\log2\pi+\frac12\log N$$
を得る。
ディリクレ級数
ディリクレ級数の解析接続
ディリクレ級数
$$L(s)=\sum^\infty_{n=1}\frac{c(n)}{n^s}$$
は一般に解析接続を考えることが難しいと思われますが、$c(x)$が
$$c(x)=\sum_{k\geq0}\frac{a_k}{x^{\a_k}}$$
(無限和とは限らない)と展開できるときは
\begin{align}
L(s)
&=\sum^\R_{n\geq1}\frac{c(n)}{n^s}+\int^\infty_1c(x)x^{-s}ds\\
&=\sum^\R_{n\geq1}\frac{c(n)}{n^s}+\sum_{k\geq0}\frac{a_k}{s+\a_k-1}
\end{align}
によって解析接続することができ、特にラマヌジャン和が正則関数を定めることから$L(s)$は$s=1-\a_k$を単純極に持つ以外は正則であることがわかったりします。
レルヒの公式
一般ディリクレ級数
$$Z(s)=\sum^\infty_{n=1}\frac1{a(n)^s}$$
に対しても同様にラマヌジャン和を考えることで次のような公式も導くことができます。
フルヴィッツのゼータ関数
$$\z(s,a)=\sum^\infty_{n=0}\frac1{(n+a)^s}$$
について
$$\z(-k,a)=-\frac{B_{k+1}(a)}{k+1}\quad(k\geq0)$$
が成り立つ。
ラマヌジャン和により
\begin{align}
\z(s,a+1)
&=\sum^\R_{n\geq1}\frac1{(n+a)^s}+\int^\infty_1\frac{dx}{(x+a)^s}\\
&=\sum^\R_{n\geq1}\frac1{(n+a)^s}+\frac{(a+1)^{1-s}}{s-1}
\end{align}
と解析接続できるので、
前回の記事
の補題4から
\begin{align}
\sum^\R_{n\geq1}(n+a)^k
&=\frac{1-B_{k+1}(a+1)}{k+1}+\int^{a+1}_1x^kdx\\
&=\frac{(a+1)^{k+1}-B_{k+1}(a+1)}{k+1}
\end{align}
が成り立つことに注意するとわかる。
数列$a_n$に対し
$$Z(s)=\sum^\infty_{n=1}\frac1{a(n)^s}$$
と定まる関数が$s=0$周りまで解析接続できるとき、$a_n$の正規化積を
$$\prod^\reg_{n\geq1}a_n=e^{-Z'(0)}$$
によって定める。
$$\prod^\reg_{n\geq1}(n+a)=\frac{\sqrt{2\pi}}{\G(a+1)}$$
$$\z(s,a+1)=\sum^\R_{n\geq1}\frac1{(n+a)^s}+\frac{(a+1)^{1-s}}{s-1}$$
を$s$について微分することで
$$\frac{\partial}{\partial s}\z(s,a+1)=-\sum^\R_{n\geq1}\frac{\log(n+a)}{(n+a)^s}-\frac{(a+1)^{1-s}}{s-1}\l(\log(a+1)+\frac1{s-1}\r)$$
特に
$$\frac{\partial}{\partial s}\z(0,a+1)=-\sum^\R_{n\geq1}\log(n+a)+(a+1)(\log(a+1)-1)$$
が成り立つので
前回の記事
の補題4から
\begin{align}
\sum^\R_{n\geq1}\log(n+a)
&=-\log\G(a+1)+\frac12\log2\pi-1+\int^{a+1}_1\log xdx\\
&=-\log\G(a+1)+\frac12\log2\pi-(a+1)(\log(a+1)-1)\\
\end{align}
と求まることに注意すると
$$\frac{\partial}{\partial s}\z(0,a+1)=\log\frac{\G(a+1)}{\sqrt{2\pi}}$$
を得る。
関数等式
最後にこのシリーズの
第$0$回
で紹介していた
\begin{align}
\z(1-s)&=2^{1-s}\pi^{-s}\cos\frac{\pi s}2\G(1-s)\z(s)\\
G_2\l(-\frac1z\r)&=z^2G_2(z)-2\pi iz
\end{align}
という関数等式のラマヌジャン和を用いた証明を見ていくこととしましょう。
ゼータ関数の関数等式
$$\sum^\R_{n\geq1}\frac1{n+u} =\log\l(1+\frac1u\r)+2\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)\frac t{u^2+t^2}dt$$
ラマヌジャン和の明示式
$$\sum^\R_{n\geq1}f(n):=\frac{f(1)}2+i\int^\infty_0\frac{f(1+it)-f(1-it)}{e^{2\pi t}-1}dt$$
において$f(x)=1/(x-1+u)$とおくことで
\begin{align}
\sum^\R_{n\geq1}\frac1{n-1+u}
&=\frac1{2u}+i\int^\infty_0\frac{\frac1{u+it}-\frac1{u-it}}{e^{2\pi t}-1}dt\\
&=\frac1{2u}+2\int^\infty_0\frac1{e^{2\pi t}-1}\frac t{u^2+t^2}dt\\
\end{align}
が成り立つので
$$\int^\infty_0\frac{dt}{u^2+t^2}=\l[\frac1u\arctan\frac tu\r]^\infty_0=\frac\pi{2u}$$
に注意すると
\begin{align}
\sum^\R_{n\geq1}\frac1{n+u}
&=\sum^\R_{n\geq1}\frac1{n-1+u}-\frac1u+\int^1_0\frac{dt}{t+u}\\
&=\log\l(1+\frac1u\r)-\frac1{2u}+2\int^\infty_0\frac1{e^{2\pi t}-1}\frac t{u^2+t^2}dt\\
&=\log\l(1+\frac1u\r)+2\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)\frac t{u^2+t^2}dt
\end{align}
を得る。
$$\z(1-s)=2^{1-s}\pi^{-s}\cos\l(\frac{\pi s}2\r)\G(s)\z(s)$$
Ramanujan's Master Theorem
の$\phi(s)=1,1/s$の場合から
\begin{align}
\int^\infty_0\frac{u^{s-1}}{1+u}du&=\frac\pi{\sin\pi s}\\
\int^\infty_0\log\l(1+\frac1u\r)u^{s-1}du&=\int^\infty_0\log(1+u)u^{-s-1}du\\
&=\frac\pi{s\sin\pi s}
\end{align}
と求まることに注意すると
\begin{align}
\int^\infty_0\l(\sum^\R_{n\geq1}\frac1{n+u}\r)u^{s-1}du
&=\sum^\R_{n\geq1}\int^\infty_0\frac{u^{s-1}}{n+u}du\\
&=\sum^\R_{n\geq1}n^{s-1}\int^\infty_0\frac{u^{s-1}}{1+u}du\\
&=\frac\pi{\sin\pi s}\sum^\R_{n\geq1}n^{s-1}\\
&=\frac\pi{\sin\pi s}\l(\z(1-s)+\frac1s\r)\\
\int^\infty_0\l(\sum^\R_{n\geq1}\frac1{n+u}\r)u^{s-1}du
&=\frac\pi{s\sin\pi s}+2\int^\infty_0\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)\frac t{u^2+t^2}u^{s-1}dt
\end{align}
つまり$0<\Re(s)<1$において
$$\frac\pi{\sin\pi s}\z(1-s)
=2\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)\int^\infty_0\frac t{u^2+t^2}u^{s-1}dudt$$
が成り立つ。
またこの右辺の積分はRamanujan's Master Theoremを二回使う(?)ことによって
\begin{align}
&\phantom{={}}
\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)\int^\infty_0\frac t{u^2+t^2}u^{s-1}dudt\\
&=\frac12\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)\int^\infty_0\frac t{u+t^2}u^{\frac s2-1}dudt\\
&=\frac{\pi/2}{\sin(\pi s/2)}\int^\infty_0\l(\frac1{e^{2\pi t}-1}-\frac1{2\pi t}\r)t^{s-1}dt\\
&=\frac{\pi/2}{\sin(\pi s/2)}(2\pi)^{-s}\G(s)\z(s)
\end{align}
と求まる。したがって
$$\frac{\sin\pi s}\pi\frac{\pi/2}{\sin(\pi s/2)}=\cos\frac{\pi s}2$$
に注意すると
$$\z(1-s)=2^{1-s}\pi^{-s}\cos\l(\frac{\pi s}2\r)\G(s)\z(s)$$
を得る。
アイゼンシュタイン級数の関数等式
アイゼンシュタイン級数とは
$$G_{2k}(z)=\sum_{m,n}\frac1{(mz+n)^{2k}}$$
のように定義される関数のことを言います。これらの関数は一般に
$$G_{2k}\l(-\frac1z\r)=\sum_{m,n}\frac{z^{2k}}{(m-nz)^{2k}}=z^{2k}G_{2k}(z)$$
という関係式を満たしますが、$k=1$のとき
$$G_{2k}(z)=\sum^\infty_{m=-\infty}\bigg(\sum^\infty_{\substack{n=-\infty\\(m,n)\neq(0,0)}}\frac1{(mz+n)^{2k}}\bigg)$$
はこの級数が条件収束となるためこのような操作が正当化されず、実際には
$$G_{2k}\l(-\frac1z\r)=z^2G(z)-2\pi iz$$
という関係式を満たすこととなります。
このことについては一般にこの$q$-展開(フーリエ級数展開)を考えることで示されますが、ラマヌジャン和を用いることで級数の形のまま示すことができます。
適当な条件下で
$$\sum^\infty_{m=1}\sum^\infty_{n=1}(f(m,n)-f(n,m))
=\int^\infty_1\int^\infty_1(f(x,y)-f(y,x))dydx$$
が成り立つ。
ラマヌジャン和においては
$$\sum^\R_{m\geq1}\sum^\R_{n\geq1}f(m,n)=\sum^\R_{m\geq1}\sum^\R_{n\geq1}f(n,m)$$
が成り立つことに注意してこれを$S$とおく。
このとき
\begin{align}
\sum^\infty_{m=1}\sum^\infty_{n=1}f(m,n)
&=\sum^\infty_{m=1}\l(\sum^\R_{n\geq1}f(m,n)+\int^\infty_1f(m,y)dy\r)\\
&=\sum^\R_{m\geq1}\sum^\R_{n\geq1}f(m,n)+\int^\infty_1\l(\sum^\R_{n\geq1}f(x,n)\r)dx
+\sum^\infty_{m=1}\int^\infty_1f(m,y)dy\\
&=S+\sum^\infty_{m=1}\int^\infty_1f(m,y)dy+\sum^\R_{n\geq1}\int^\infty_1f(x,n)dx
\end{align}
および同様に
$$\sum^\infty_{m=1}\sum^\infty_{n=1}f(n,m)
=S+\sum^\infty_{m=1}\int^\infty_1f(x,m)dx+\sum^\R_{n\geq1}\int^\infty_1f(n,y)dy$$
が成り立つのでこの差を取ることで
\begin{align}
\sum^\infty_{m=1}\sum^\infty_{n=1}(f(m,n)-f(n,m))
&=\sum^\infty_{m=1}\int^\infty_1(f(m,y)-f(y,m))dy\\
&\qquad-\sum^\R_{m\geq1}\int^\infty_1(f(m,y)-f(y,m))dy\\
&=\int^\infty_1\int^\infty_1(f(x,y)-f(y,x))dydx
\end{align}
を得る。
$$G_{2k}\l(-\frac1z\r)=z^2G(z)-2\pi iz$$
\begin{align}
G_{2k}(z)
&=2\sum^\infty_{m=1}\sum^\infty_{n=1}\l(\frac1{(mz+n)^2}+\frac1{(mz-n)^2}\r)
+2\l(1+\frac1{z^2}\r)\z(2)\\
\frac1{z^2}G_{2k}\l(-\frac1z\r)
&=2\sum^\infty_{m=1}\sum^\infty_{n=1}\l(\frac1{(nz+m)^2}+\frac1{(nz-m)^2}\r)
+2\l(1+\frac1{z^2}\r)\z(2)
\end{align}
と表せることに注意すると
$$f(m,n)=\frac1{(mz+n)^2}+\frac1{(mz-n)^2}$$
に対し
$$\sum^\infty_{m=1}\sum^\infty_{n=1}(f(m,n)-f(n,m))=\frac{\pi i}z$$
が成り立つことを示せばよい。
そしてこれは上の補題から
\begin{align}
\sum^\infty_{m=1}\sum^\infty_{n=1}(f(m,n)-f(n,m))
&=\int^\infty_1\int^\infty_1(f(x,y)-f(y,x))dydx\\
&=-\frac1z\l[\log\frac{x+z}{x-z}-\log\frac{1+xz}{1-xz}\r]^\infty_1\\\
&=\frac{\pi i}z
\end{align}
とわかる。
おわりに
以上がラマヌジャン総和法に関する理論の概説でした。
最初
$$\sum^\R_{n\geq1}f(n)=\frac{f(1)}2-\sum^\infty_{n=1}\frac{B_{2n}}{(2n)!}f^{(2n-1)}(1)$$
という定義が出てきたときは一体この謎の定数から何がわかるのかと思いましたが
$$R(x)-R(x+1)=f(x),\quad\int^2_1R(x)dx=0$$
という方程式によって特徴付けられる関数
$$R(x)=-\int^x_1f(t)dt+\frac{f(x)}2+i\int^\infty_0\frac{f(x+it)-f(x-it)}{e^{2\pi t}-1}dt$$
が正則関数の積分変換という解析的に扱いやすい対象となっているため、例えばゼータ関数の解析接続
$$\z(s)=\sum^\R_{n\geq1}n^s+\frac1{s-1}$$
を定めるなど重要な結果をもたらしてくれるのでした。
結局アベル・プラナの和公式やメリン変換のような積分変換が偉いだけじゃね？と思うところもままありますが、総和法として$\sum$を用いて表すことで議論が明瞭になるというのは確かです。
総和法は雰囲気だけで使っていると非常に危ういものではありますが、正しい使い方を知っていれば怖いものはありません。比較的幅広く使える総和法として中々面白い武器を手に入れたという感触があります。
皆さんもラマヌジャン総和法を用いて色々遊んでみてはいかがでしょうか。
では。
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
