Nielsen-Ninomiyaの定理1/2: Poincaré-Hopfの定理
物理学と関連する指数定理に関していくつか記事を書きました（Refs.anomalyDirac_zeromodeWitten）。本記事と次の記事で、そのような定理のひとつである「Nielsen-Ninomiyaの定理」（Refs.NielsenAokiKarsten）に関して書きます。
Nielsen-Ninomiyaの定理とは、場の理論においてfermionを格子正則化した際、ある物理的に自然な条件の下では連続極限に存在しないモード ーdoublerと呼ばれるー が生ずるのを避けられないというno-go定理です。この定理に関しては次の記事で説明します。
ところで、球面に毛を生やすと必ずつむじができるという事実はよく知られています。Nielsen-Ninomiyaの定理は、このつむじの存在と関わる定理である「Poincaré-Hopfの定理」:
\begin{align}
\sum_r j_r=\chi(S) \ \ \ \ (j_r\text{は特異点の指標。}S\text{は向き付可能な閉曲面。}\chi(S)\text{は閉曲面のEuler標数})
\end{align}
を用いることで証明できます。
本記事ではこの「拡張されたつむじ定理 = Poincaré-Hopfの定理」を、Ref.Hopfに習い証明します。ここでは向き付け可能な2次元閉曲面に関する当該定理を扱います。次の記事で格子正則化およびdoublerを説明し、この定理を用いることでNielsen-Ninomiyaの定理を証明します。
準備：ベクトル場の特異点とその指数、三角形分割
ベクトル場の特異点・その指数
向き付け可能な2次元の閉曲面を考えます。閉曲面とはコンパクトで境界のない2次元曲面のことです。向き付け可能とは、Ref.Kobayashiの表現を借りると、閉曲面を三角形分割した際2つの三角形領域で共有されている辺の向き付けがすべての2つの三角形領域で逆になる場合を言います。三角形分割、辺の向き付けに関しては後ほど述べます。
まあでも本記事ではヘンな曲面は考えないこととし、「向き付け可能な2次元の閉曲面」＝「裏表が定義できる閉じた曲面」と感覚的に捉えて問題ないです。
閉曲面の各点の接平面上に連続なベクトル場をとります。つまりは閉曲面上の各点に曲面に沿って矢印を描くのですが、有限個の孤立したベクトル場のゼロ点の近傍を除き、十分近くの矢印はほとんど同じ長さと向きを持つことにします。一方ゼロ点の近傍ではベクトル場の向きは一般には連続的に変化しません。例えば図1のようなつむじはその例です。なぜならつむじでは、そこからほんのちょっと離れた2点でも毛の方向が全く異なるからです。また簡単な例として極座標表示されたベクトル場${\boldsymbol v}=(r\cos\theta,r\sin\theta)$の原点はゼロ点であり、その点をまたぐとベクトルの方向は不連続に変化します。以降このようなゼロ点を特異点と呼ぶことにします。
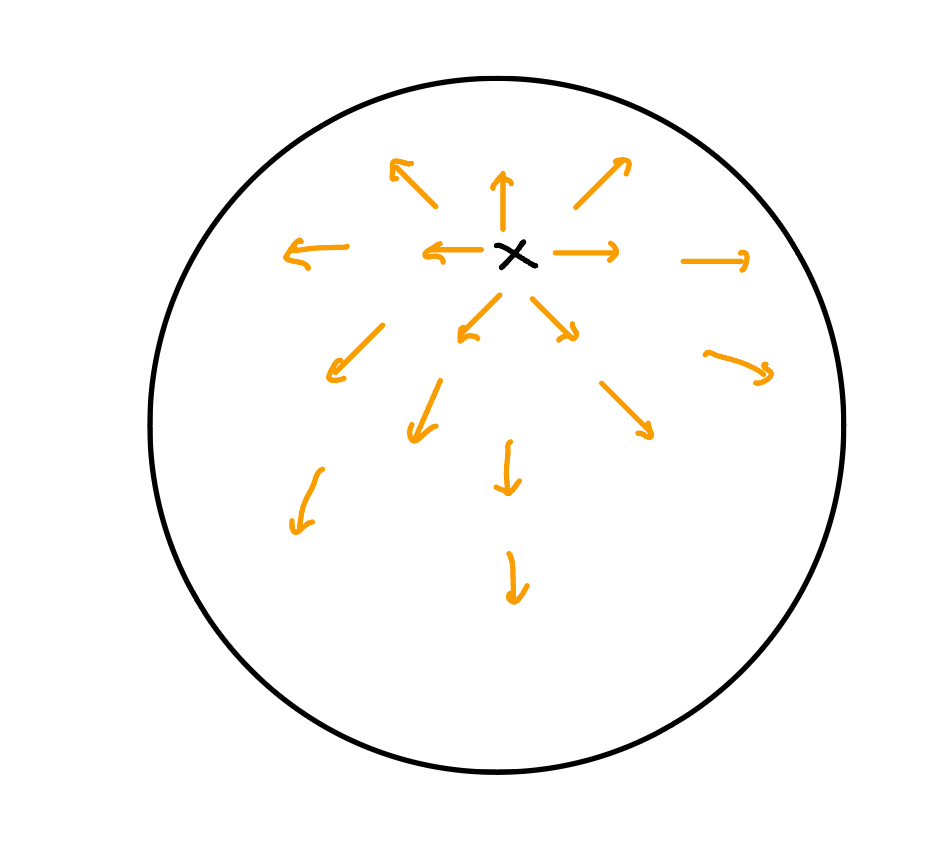球面上のベクトル場の例。バツ印はつむじ。
特異点の周りを囲む小さな経路をとります（図2）。この経路上ではベクトル場は連続的に変化します。経路を一周して戻ればもちろんベクトル場は同じ方向を向いています。しかも連続的に変化するので、一周回った時に経路上のベクトルがどれだけ回転したかが定義できます。回転角は$2\pi$の整数倍になります。これを$2\pi$で割った値を、その特異点の指数と呼びます。例えば反時計回りにベクトルが一周するなら指数は$+1$、時計回りに一周なら$-1$、回らないなら$0$です（図2）。
![特異点の指数の例。!FORMULA[7][37918][0]が指数。円内の赤点は特異点。黒矢印は経路の方向。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FgYTCkVxs2ZuRZ7nu8FIa.png?alt=media)
特異点の指数の例。$j$が指数。円内の赤点は特異点。黒矢印は経路の方向。
経路には向きがあり、それによりベクトルの回転方向が逆になるのは重要です。図2では円周左回りに対して矢印の回転角を測っていますが、もし右回りだと指数の正負が逆になります。特異点がある領域を左手に見る方向に経路を向き付けるのがルールです。
回転角は$2\pi$の整数倍だから、特異点の指数は離散的な値です。よって指数は少しだけ変わるということが不可能です。よって連続的な経路の変形に対し指数は変化しません。ゆえに指数では経路が特異点を囲うか否かというトポロジカルな性質が重要です。領域内に特異点がない場合、その経路が十分小さければ経路に沿ったベクトル場の変化は無限に小さくできるので、指数はゼロです。
三角形分割
以下に示す証明では閉曲面を「三角形分割」することが重要です。その名のとおり閉曲面を三角形で分割するのですが、いくつかルールがあります。まず三角形と言っても辺がまっすぐである必要はありません。また頂点・辺だけではなくその領域内部も含みます（これを三角形の面と呼びます）。さらに曲面$S$の三角形分割では以下のような条件がつきます（Ref.Kobayashi）：
- $S$の1点$P$が三角形$T$に属し、かつその辺上になければ、$T$が$P$を含む唯一の三角形であり、
- $P$が三角形$T$の辺上にあってその頂点でなければ、$P$の属する辺を共有する三角形$T'$がちょうどもう1つあり、$P$は$T\cup T'$の内部に含まれ、
- $P$が三角形$T$の頂点なら、$P$を頂点とする有限個の三角形$T=T_1,T_2,\cdots,T_k$があり、$T_j$と$T_{j+1}$はただ1つの辺を共有し（ただし$T_{k+1}=T_1$と考える）、かつ$P$は$T_1\cup\cdots \cup T_k$の内部に含まれる
三角形分割では、ある点が頂点なら、それを共有するどの三角形でもその点は頂点です。ある三角形の頂点が他の三角形の頂点ではない辺上にあってはダメです。このようなルールを守って三角形に分割します。
Poincaré-Hopfの定理
以上の準備のもと以下の定理を示します。
向き付け可能な閉曲面$S$の特異点の指数の和はEuler標数$\chi(S)$に等しい:
\begin{align}
\sum_r j_r=\chi(S), \ \ \ \chi(S):=v-e+f
\end{align}
ここで$v,e,f$はそれぞれ$S$を三角形分割したときの頂点、辺、面の数。
まず特異点の指数の和がベクトル場の取り方に依存しないことを示す。
閉曲面$S$上の2つの違うベクトル場$F,F'$を用意し、$S$を$F,F'$の特異点がそれぞれ最大でも1つ入るように三角形分割する。三角形分割のそれぞれの領域に番号を割り振り、その番号を$r$で表す。各領域における$F,F'$の特異点の指数をそれぞれ$j_r,j'_r$とする（特異点が内部にない場合は指数はゼロ）。2つのベクトル場の回転の様子とそれぞれの特異点の指数、指数の差を図3に示した（$F$が赤、$F'$が青）。
![三角形分割の各領域の辺上における2つのベクトル場（!FORMULA[44][36802][0]が赤、!FORMULA[45][1140991][0]が青）。赤と青の点はそれぞれ!FORMULA[46][1096675225][0]の特異点を表す。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FMT13P0awmH0KqKFICFcR.png?alt=media)
三角形分割の各領域の辺上における2つのベクトル場（$F$が赤、$F'$が青）。赤と青の点はそれぞれ$F,F'$の特異点を表す。
さて、指数の差の和$\sum_r(j_r-j'_r)$を考える。三角形$r$において、$j_r-j'_r$は辺に沿ってベクトル場が1周したときの各ベクトルの回転角の差である（図4参照）。ここで各辺は2つの三角形領域で共有される。またその経路の方向は、その辺を共有する2つの三角形領域で逆になる: 図4において薄いオレンジの矢印$A$が領域$A$における経路の向き、矢印$B$が領域Bにおける経路の向きである。よって図4の赤と青のなすベクトルの角度の変化は、$A$と$B$で絶対値が等しくかつ符号が逆である。以上から、ある辺からの$j_r-j'_r$への寄与は、その辺を共有する2つの三角形領域で打ち消しあう。
![２つの三角形領域!FORMULA[56][35227537][0]が共有する辺におけるベクトル場!FORMULA[57][1096675225][0]の変化。辺上に薄いオレンジで示した矢印は、三角形!FORMULA[58][36647][0]および!FORMULA[59][36678][0]での経路の方向を示す。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FXfJeJ8eiL7c3M3PjuFhi.png?alt=media)
２つの三角形領域$A,B$が共有する辺におけるベクトル場$F,F'$の変化。辺上に薄いオレンジで示した矢印は、三角形$A$および$B$での経路の方向を示す。
よってすべての三角形からの$j_r-j'_r$の寄与の和をとるとゼロになる：
\begin{align}
\sum_r (j_r-j'_r)=0
\end{align}
三角形領域が特異点を含まないときは$j_r,j'_r$はゼロなので、和は特異点に関してとればよい。よって特異点の指数の和はベクトル場の取り方に依存しない(★)ことがわかる：
\begin{align}
\sum_r j_r=\sum_{r'} j'_{r'}
\end{align}
上の式の$r, r'$はそれぞれベクトル場$F,F'$の特異点につけた番号である。
(★)の事実から、ある特定のベクトル場で特異点の指数の和を計算すれば、その値は一般のベクトル場で正しい。そこで以下、特異点の指数の和が曲面$S$のEuler標数に等しいベクトル場が作れることを示す。
閉曲面$S$を適当に三角形分割する。そしてそれぞれの三角形領域に、図5の右図のように新たな点を4つ付け加える。赤で示した3点は各辺の中心に位置している。また青の1点は辺や頂点には存在せず、面の真ん中あたりに位置するとする。そして赤、青および三角形の頂点を図のように線で結ぶ。
このようにして新たにできた図形の各線分に図5のように矢印を付与する。矢印のルールは以下：
- 元の三角形の辺に位置する線分には、赤の点に向かって矢印をつける
- 青い点を通る線分に関しては、青い点に向かって矢印をつける
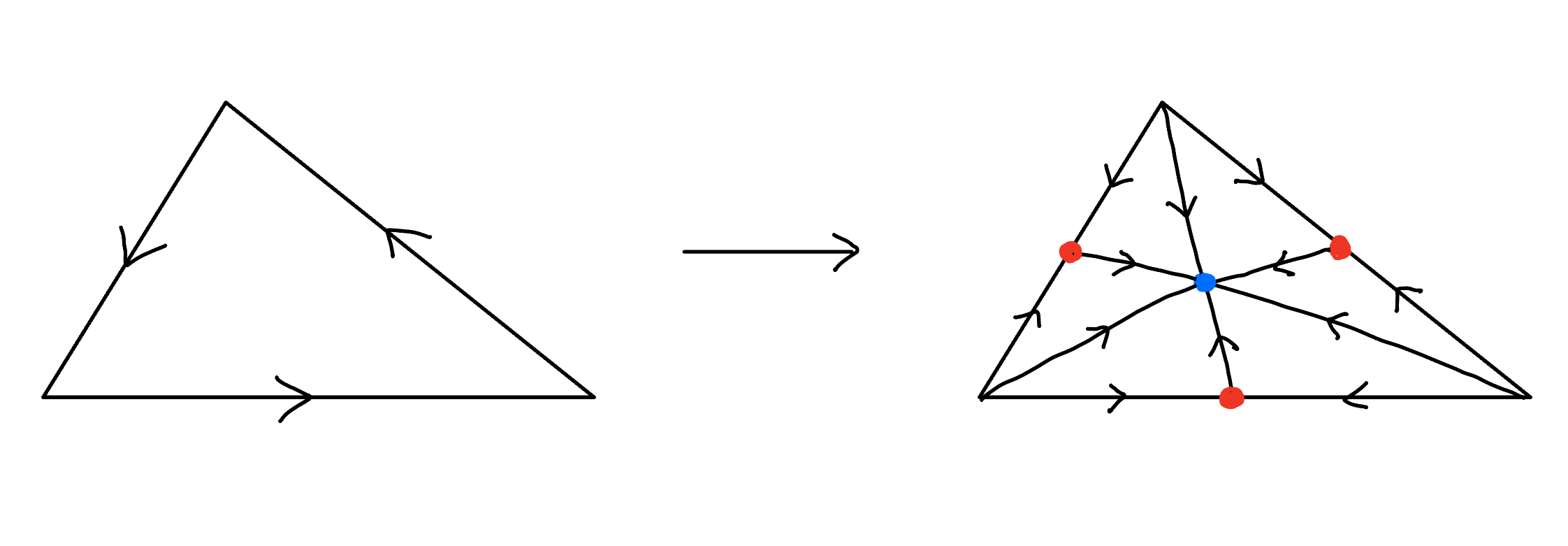三角形領域に4点（辺上の赤3点、面内の青1点）を加え、線で結び、矢印を付す。
さて、この矢印に整合的なベクトル場を局面$S$に作る。元の三角形は、4点の追加により新たに6つの三角形領域に分割されるが、その各々の領域内部では、滑らかな特異点のないベクトル場が作れる。これは図6から直感的に明らかかと思う。
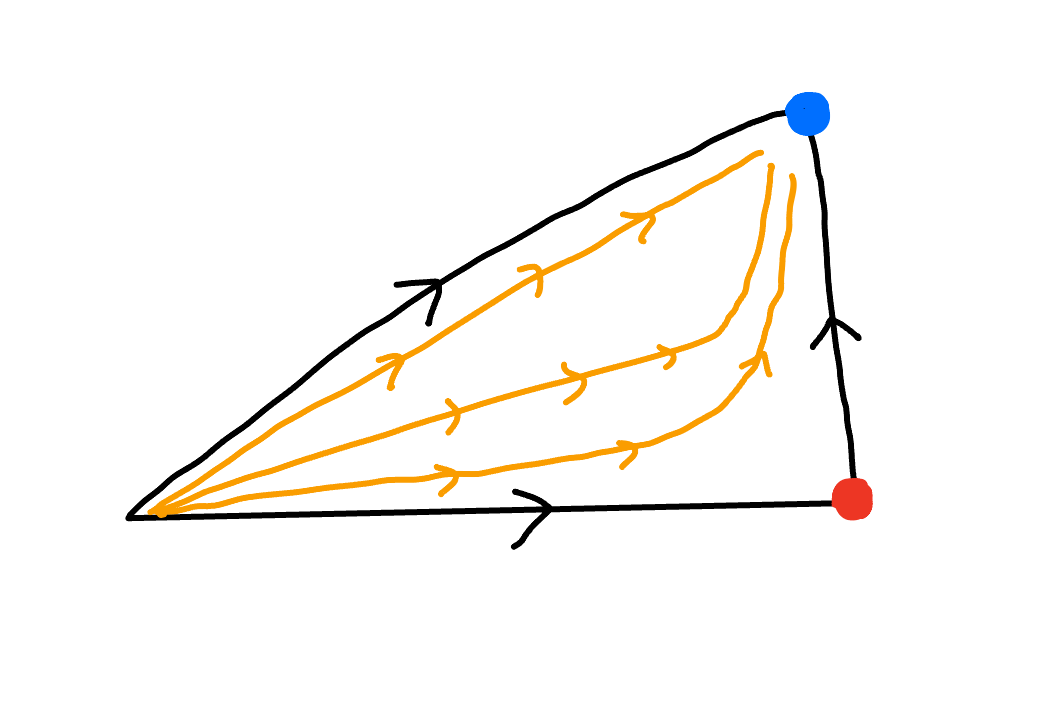図5右図左下の三角形内部のベクトル場の例。内部には特異点が生じないように描ける。
特異点は図7の青、赤、緑の点である。図7の各特異点のまわりのベクトル場の様子より、それぞれの特異点の指数は
青: $+1$、赤: $-1$、緑: $+1$
である。
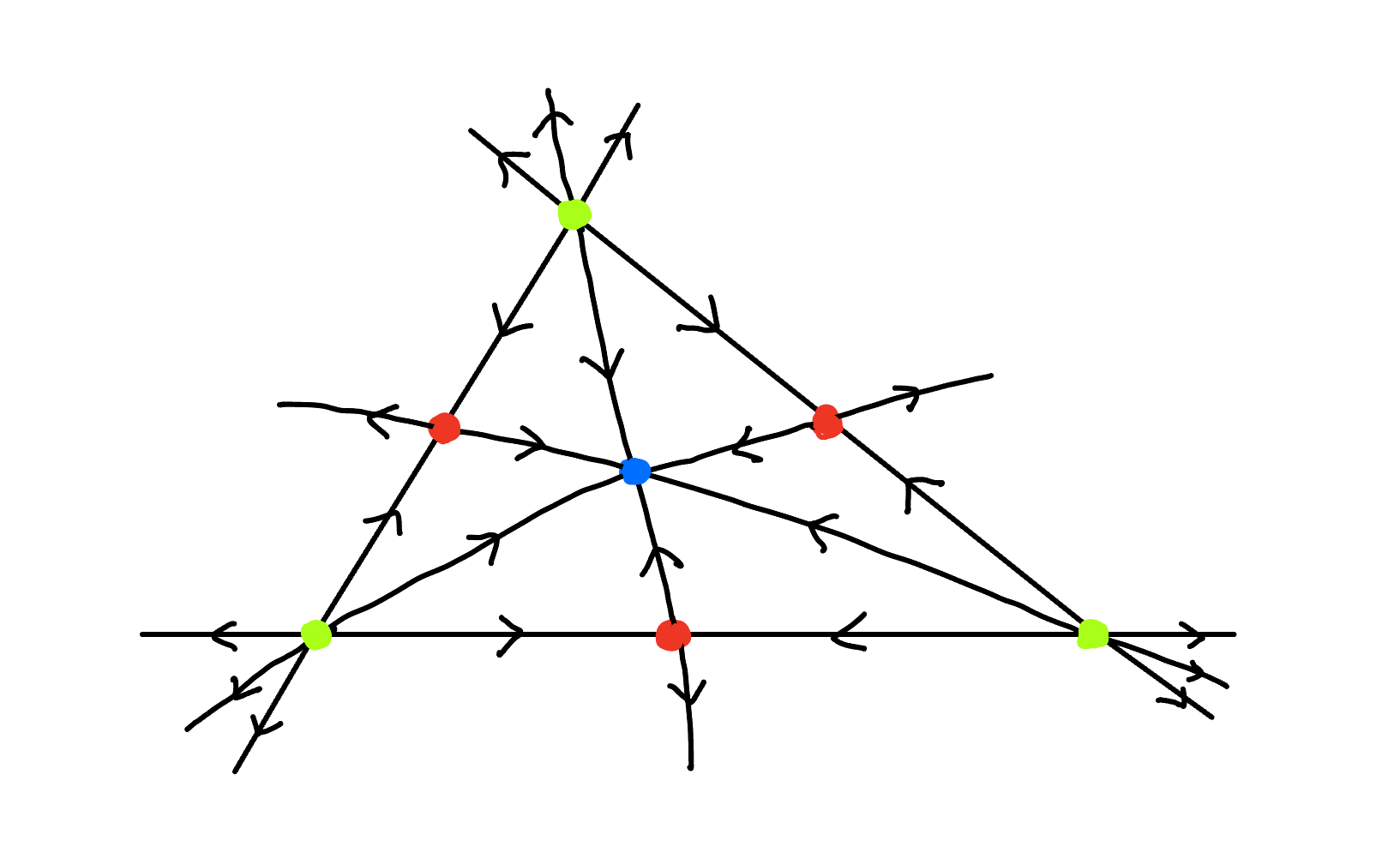緑・赤・青の特異点のまわりのベクトル場の様子。面内のベクトル場は省略してある。
青は元の三角形分割の面の数$f$、赤は辺の数$e$、緑は頂点の数$v$だけ存在する。ゆえに閉曲面の指数$j_r$の和は
\begin{align}
\sum_r j_r=v\times(+1)+e\times(-1)+f\times(+1)=v-e+f
\end{align}
であることがわかる。$v-e+f$はEuler標数なので、定理1が証明された。${}_\blacksquare$
球面を三角形分割しEuler標数を計算すれば$2$であることがわかるので、必ず特異点=つむじが必要です。Euler標数は2だから、指数が$+1$の特異点なら2つ必要です。これは、例えば球の南極から湧き出し北極に吸い込まれるようなベクトル場を考えれば指数が$+1$の特異点が2つ存在することと整合的です。
この定理により、特異点がない閉曲面はEuler標数がゼロである必要があります。そのような図形はトーラス（＝ドーナツ）です。つむじがないようにトーラスに毛を（寝かせて）生やすには、例えばベクトル場をトーラスの周に沿うように描けばよいです。
今回はここまで。${}_\blacksquare$
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
