文献あり

超幾何数列の基礎12：機械計算のすゝめ

103

はじめに

　この記事では前回の記事に引き続き超幾何数列の基本事項についてまとめていきます。
　さてこれまでの記事では超幾何数列の計算に関する各種アルゴリズムの手順と正当性について解説し、また第10回・第11回の記事ではそれらを手計算で実行する際のコツについて紹介しました。しかしこれまでも何度か言及しているように各種のアルゴリズムは時に非常に膨大な計算を要するため、手計算で実行するのはあまり現実的ではありません。
　なので基本的には適当な数式処理ソフトに計算を任せた方が良いわけですが、GosperやZeilbergerのアルゴリズムを直接実行できるコマンドが用意されているのは"A=B"などで紹介されているMapleという有償ソフトくらいしかなく、そのため私の記事では特に紹介してきませんでした。
　しかしどうやら無償ソフトである Maxima にも超幾何数列の計算に関するコマンドが用意されているらしいということを最近知ったので、今回の記事ではそのことついて簡単に調べていこうと思います。

基本的な使い方

　とりあえずMaximaの操作方法について最低限の説明をしておきましょう。本当に最低限の説明しかしないので、詳しい使い方については各々で調べてください。

ダウンロードは各々で頑張って。オンラインで実行できるサイトもあるっぽいので、ダウンロードがめんどくさい人やスマホから実行したい人はこちらを試してみてはいかが。
Maximaはコマンドプロンプトとかからも呼び出せるらしいが、wxMaximaを使うと数式が見やすくて良いらしい。
実行結果を出力する場合は末尾に ; を、しない場合には $ を打ち込み、Shift+Enterを押すことでコマンドが実行される。
単にEnterを押すと改行でき、縦または横並びにコマンドを書いてShift+Enterを押すことで複数のコマンドをいっぺんに実行できる(コマンドの数だけラベルが付与される)。
${}$: で代入操作が、:= で関数の定義ができる。
TeXとかDesmosとかWolframAlphaとかに慣れてると忘れがちなこととして、(一部例外はあるが)あらゆる積に対し * を打たなければならないことに非常に注意しよう。incorrect syntax系のエラーメッセージが出たときはまず * の打ち忘れを疑った方がいいと思う(個人の感想)。

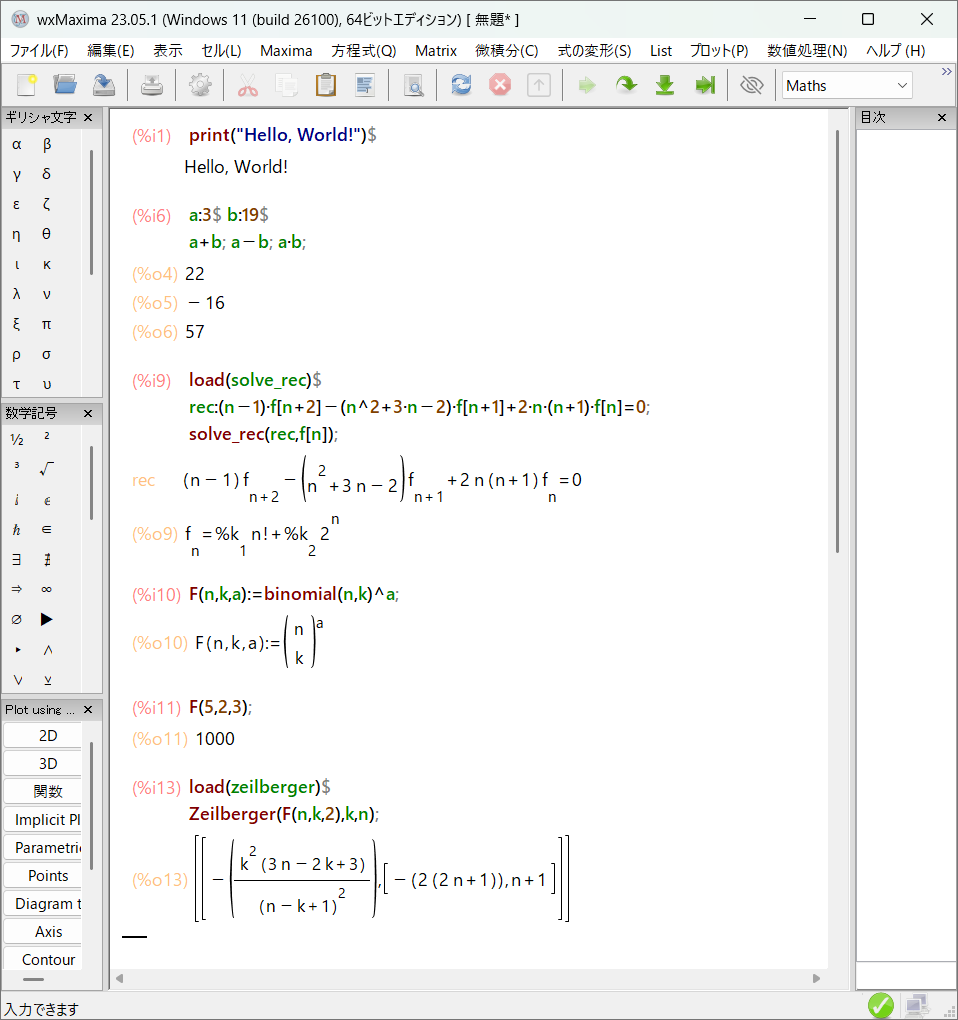使用例

simplify_sumパッケージ

　まずは Gosper's algorithm および Zeilberger's algorithm に類する計算を実行できるパッケージ：simplify_sumについて解説していきましょう。
　ただしこれらのアルゴリズムに関しては下で紹介するZeilbergerパッケージでも扱うことができ、それぞれ違った特性を持つので、上手く使い分けるようにしましょう。

パッケージの内容

　このパッケージには主にsimplify_sum, summand_to_recの2つのコマンドが用意されています。これらのコマンドを使うためには予めload(simplify_sum)を実行しておく必要があります。

sum(A(n), n, a, b)
数列$A(n)$とその変数$n$および始点と終点$a,b$を与えたとき$\sum^b_{n=a}A(n)$を返します。簡単な数列$A(n)$に対してはその値や閉形式を返します。
simplify_sum(S)
sum(hoge)の含まれた数式$S$を与えたとき、その数式中のsumをできるだけ閉形式に表そうとします。
summand_to_rec(F(n,k), [k,a,b], n)
超幾何数列$F(n,k)$とその変数$n,k$および始点と終点$a,b$を与えたとき
$$\sm_n=\sum^b_{k=a}F(n,k)$$
の満たす漸化式を返します。また$a,b$を省略した場合は
$$\sm_n=\sum^\infty_{k=-\infty}F(n,k)$$
の満たす漸化式を返します。

計算例と補足

　simplify_sumパッケージの基本的な機能は上に記した通りですが、細かいことについては以下で計算例を眺めながら説明していくこととしましょう。(なお以下の例における表記は実際の挙動とはラベルの付き方などが少し異なりますが、あまり気にしないでください。)

$k^{10}$の総和

(%i1)    load(simplify_sum)$
(%i2)    sum(k^(10), k, 1, n);

$$(\%\o2)\qquad\sum^n_{k=1}k^{10}$$

(%i3)    simplify_sum(%);

$$(\%\o3)\qquad\frac{6n^{11}+33n^{10}+55n^9-66n^7+66n^5-33n^3+5n}{66}$$

(%i4)    factor(%o3);

$$(\%\o4)\qquad \frac{n(n+1)(2n+1)(n^2+n-1)(3n^6+9n^5+2n^4-11n^3+3n^2+10n-5)}{66}$$

　上のように引数に$\%$を入れるとで直前の出力を参照することができ、また$\%\o3$のようにラベルを指定することで該当の出力を参照することができます。
　またfactorを用いることで数式を因数分解することができます。

partfracの使用例

(%i1)    load(simplify_sum)$
(%i2)    S: sum(1 / (k^2 + sqrt(5)*k -1), k, 1, n);
(%i3)    simplify_sum(S);

\begin{align} \mathrm{S}\qquad&\sum^n_{k=1}\frac1{k^2+\sqrt5k-1}\\ (\%\o3)\qquad&\frac{32n(3\sqrt5n^2+7n^2+12\sqrt5n+24n+9\sqrt5+23)}{3(\sqrt5-1)(\sqrt5+1)(\sqrt5+3)(2n+\sqrt5-1)(2n+\sqrt5+1)(2n+\sqrt5+3)} \end{align}

(%i4)    partfrac(%, n);

\begin{align} (\%\o4)\qquad -\frac{4\sqrt5+4}{(6\sqrt5+6)(2n+\sqrt5+3)} &+\frac{-4\sqrt5-4}{(6\sqrt5+6)(2n+\sqrt5+1)}\\ &-\frac{16\sqrt5+32}{(24\sqrt5+48)(2n+\sqrt5-1)} +\frac{12\sqrt5+28}{12\sqrt5+36} \end{align}

　このようにpartfrac(hoge, n)を用いて計算結果を$n$について部分分数分解することで式が多少綺麗になる場合があります。ただしこの例の場合では後の例でも紹介するようにAntiDifferenceを用いた方が結果が綺麗になるので、そのあたりは上手く使い分けるようにしましょう。

超幾何数列の入力について

(%i1)    load(simplify_sum)$
(%i2)    A: (3*n)! / (n! * (n+1)! * (n+2)! * 27^n)$
(%i3)    B: (n-1)!^2 / ((n-1/2)! * (n+1/2)!)$
(%i4)    C: gamma(n-1/4) / gamma(n+1/4)$
(%i5)    D: product(a*j^3 + b*j^2 +c*j + d, j, 1, n-1) / product(a*j^3 + b*j^2 +c*j + e, j, 1, n)$
(%i6)    List: [A, B, C, D];

$$\mathrm{List}\qquad\l[ \frac{(3n)!}{27^nn!(n+1)!(n+2)!},\ \frac{(n-1)!^2}{(n-\frac12)!(n+\frac12)!},\ \frac{\G(n-\frac14)}{\G(n+\frac14)},\ \frac{\prod^{n-1}_{j=1}(aj^3+bj^2+cj+d)}{\prod^n_{j=1}(aj^3+bj^2+cj+e)}\r]$$

(%i7)    S(x) := simplify_sum(sum(x, n, 1, m))$
(%i8)    for k:1 thru 4 do print(S(List[k]));

\begin{align} &\frac{(81m^2+261m+200)(3(m+1))!}{120(m+1)27^mm!(m+1)!(m+2)!}-5\\\\ &\frac{4m!^2}{(\frac{2m-1}2)!(\frac{2m+1}2)!}-\frac8\pi\\\\ &\frac{2\,\G(\frac{4m+3}4)}{\G(\frac{4m+1}5)}-\frac{2\,\G(\frac34)}{\G(\frac14)}\\\\ &\frac{e+c+b+a}{(e-d)\prod^1_{j=1}(aj^3+bj^2+cj+e)}-\frac{\prod^n_{j=1}(aj^3+bj^2+cj+d)}{(e-d)\prod^n_{j=1}(aj^3+bj^2+cj+e)}\\\\ (\%\o8)\qquad&\mathrm{done} \end{align}

　このようにsimplify_sumパッケージでは超幾何数列を入力する方法として有理関数、指数関数、階乗、二項係数(binomial)、ガンマ関数(gamma)、総乗(product)などが全て使えます。ただし下で紹介するZeilbergerパッケージやsolve_recパッケージではどうやらガンマ関数と総乗は超幾何数列として認識してくれないっぽいので、上手く使い分けるようにしましょう。
　また上のようにリストや関数の定義、for文などが使えます(詳しくは各々で調べてください)。

二変数の総和

(%i1)    load(simplify_sum)$
(%i2)    F(a):= sum(binomial(n,k)^a, k, 0, n);

$$(\%\o2)\qquad F(a):=\sum^n_{k=0}\binom nk^a$$

(%i3)    for a:1 thru 3 do print(F(a));

\begin{align} &2^n\\\\ &\frac{2^{2n}(\frac{2n-1}2)!}{\sqrt\pi n!}\\\\ &\sum^n_{k=0}\binom nk^3\\\\ (\%\o3)\qquad&\mathrm{done} \end{align}

　このようにsimplify_sumはZeilberger's algorithmの範疇にあるような総和の閉形式もできるだけ求めようとしてくれます。ただし時により
$$\sum^n_{k=0}\binom nk^2=\frac{2^{2n}(\frac{2n-1}2)!}{\sqrt\pi n!}\qquad\l(=\frac{2^{2n}(\frac12)_n}{(1)_n}=\binom{2n}n\r)$$
のように少しクセのある形式で表示されることには注意しましょう。

summand_to_recの使用例

(%i1)    load(simplify_sum)$
(%i2)    summand_to_rec(binomial(n,k)*x^k, k, n);
(%i3)    summand_to_rec(binomial(n+k,k)*2^(-k), [k,0,n], n);
(%i4)    summand_to_rec(binomial(n+k,k)*2^k, [k,0,n], n);

\begin{align} (\%\o2)\qquad&\sm_n\c(x+1)-\sm_{n+1}=0\\\\ (\%\o3)\qquad&\sm_{n+1}-2\sm_{n+1}=0\\\\ (\%\o4)\qquad&\sm_{n+1}+\sm_{n+1}=\frac{3\c2^{n+1}(2n+1)!}{(n+1)n!^2} \end{align}

　これはつまり
$$f_1(n)=\sum^\infty_{n=-\infty}\binom nkx^k=\sum^n_{k=0}\binom nkx^k$$
および
$$f_2(n)=\sum^n_{k=0}\binom{n+k}k\frac1{2^k},\quad f_3(n)=\sum^n_{k=0}\binom{n+k}k2^k$$
とおいたとき、これらが漸化式
\begin{alignat}{3} f_1(n+1)-{}&&(x+1)f_1(n)&=0\\ f_2(n+1)-{}&&2f_2(n)&=0\\ f_3(n+1)+{}&&f_3(n)&=\frac{3\c2^{n+1}(2n+1)!}{(n+1)n!^2} \end{alignat}
を満たすことを意味しています。
　Zeilberger's algorithmを応用したい場合は基本的にはこのsummand_to_recを用いるのが便利だと思いますが、これは有限和にしか使えないっぽい、つまり
$$f(k)=\sum^\infty_{n=k}\binom nky^n$$
のような無限級数の満たす漸化式を求めるのが苦手っぽかったり、また漸化式の成立を証明するのに必要な$G(n,k)$を提示してくれなかったりするので、そういう時は下で紹介するZeilbergerを用いるようにしましょう。

Zeilbergerパッケージ

　次に Gosper's algorithm および Zeilberger's algorithm を実行できるもう一つのパッケージであるZeilbergerパッケージについて解説していきましょう。
　これを呼び出すためには予めload(zeilberger)というコマンドを実行しておく必要があります。

Gosper's algorithm

　Gosper's algorithmに関するコマンドはAntiDifference, Gosper, GosperSumの3つが用意されています。

AntiDifference(A(n),n)
超幾何数列$A(n)$とその変数$n$を指定したとき、$A(n)=T(n+1)-T(n)$を満たすような超幾何数列$T(n)$を返します。そのような$T(n)$が存在しないときはNO_HYP_ANTIDIFFERENCEを返します。
Gosper(A(n),n)
同じく$T(n)$が存在すれば有理関数$T(n)/A(n)$を返し、存在しなければNO_HYP_SOLを返します。
GosperSum(A(n),n,a,b)
同じく$T(n)$が存在すれば和$\sum^b_{n=a}A(n)=T(b+1)-T(a)$を返し、存在しなければNON_GOSPER_SUMMABLEを返します。

Zeilberger's algorithm

　Zeilberger's algorithmに関するコマンドはparGosper, Zeilbergerの2つが用意されています。

parGosper(F(n,k),k,n,d)
超幾何数列$F(n,k)$とその変数$n,k$を指定したとき
$$\sum^d_{i=0}p_i^{(j)}(n)F(n+i,k)=G^{(j)}(n,k+1)-G^{(j)}(n,k)$$
を満たすような多項式$p_i^{(j)}(n)$と超幾何数列$G^{(j)}(n,k)$をリスト
$$\l[\l[\frac{G^{(1)}(n,k)}{F(n,k)},[p^{(1)}_0,p^{(1)}_1,\ldots,p^{(1)}_d]\r], \l[\frac{G^{(2)}(n,k)}{F(n,k)},[p^{(2)}_0,p^{(2)}_1,\ldots,p^{(2)}_d]\r],\ldots\r]$$
の形で返します。解が求まらないときは空のリスト[]を返します。
Zeilberger(F(n,k),k,n)
parGosperを$d=1$から順に解が求まるか$d$がMAX_ORD(デフォルトは$5$)に達するまで実行し、解が求まれば対応するリストを、求まらなければ空のリスト[]を返します。

注意

　上でも言及したようにZeilbergerパッケージとsolve_recパッケージのコマンドではガンマ関数や総乗は超幾何数列とみなされないことに注意しましょう。
　したがって例えばポッホハマー記号$(a)_n$は(n+a-1)!/(a-1)!と表したり、$A(n)=\prod^n_{k=1}(k^2+1)$のような超幾何数列は無理やり因数分解して(n+%i)!*(n-%i)!/(%i!*(-%i)!)と表す必要があります(%iはMaximaにおける虚数単位)。

計算例と補足(Gosper)

$A(n)=n^{10}$のAntiDifference

(%i1)    load(zeilberger)$
(%i2)    AntiDifference(n^10, n);

$$(\%\o2)\qquad \frac{n^{11}}{11}-\frac{n^{10}}2+\frac{5n^9}6-n^7+n^5-\frac{n^3}2+\frac{5n}{66}$$

(%i3)    simplified_output: true$
(%i4)    AntiDifference(n^10, n);

$$(\%\o4)\qquad \frac{(n-1)n(2n-1)(n^2-n-1)(3n^6-9n^5+2n^4+11n^3+3n^2-10n-5)}{66}$$

　このようにsimplified_outputにtrueを代入しておくと計算結果をいい感じに通分したり因数分解したりしてくれるようになります(却って煩雑になることもあるので注意)。
　また Gosper's algorithm による出力
$$T(n)=x(n)\c\frac{b(n)}{c(n)}A(n)$$
において$b(n)/c(n)$の部分は$A(n)$の適当な因子と約分できるのに対し、simplified_outputでは多項式同士の約分までしかしてくれません。それが気になる場合は

factor：数式の因数分解をする
ratsimp：有理式の通分とか約分とかをする
factcomb：階乗に掛かっている多項式を階乗の中に入れたりする
minfactorial：階乗同士の約分をしたり、数式内の階乗の引数を揃えたりする
factorial_expand：trueを代入しておくと階乗の引数を揃えるようになる

などのコマンドによって式を整理することができます。
　ただfactcombの挙動には少しクセがあるため、それを補正するためにratsimpやfactorも併用した方が良く、つまりは困ったらとりあえず

factor(ratsimp(factcomb( hoge )))
factor(ratsimp(minfactorial( hoge )))
factor(ratsimp(minfactorial(factcomb( hoge ))))

などを試してみるといいと思います。
　とはいえやっぱりfactcombがクセモノ過ぎるので、手頃なコマンドであんまり上手くいかない場合は手動で整理した方が手っ取り早い気もします。

計算結果の簡約化

(%i1)    load(zeilberger)$
(%i2)    (3*n)! / (n! * (n+1)! * (n+2)! * 27^n);

$$(\%\o2)\qquad\frac{(3n)!}{27^nn!(n+1)!(n+2)!}$$

(%o3)    simplified_output: true$
(%i4)    AntiDifference(%, n);
(%i5)    minfactorial(%);

\begin{align} (\%\o4)\qquad&\frac{9(n+1)(n+2)(81n^2+99n+20)(3n)!}{40\c27^nn!(n+1)!(n+2)!}\\\\ (\%\o5)\qquad&\frac{9(81n^2+99n+20)(3n)!}{40(n+1)27^nn!^3} \end{align}

(%o6)    fractorial_expand: true$
(%i7)    (3*n)! / (n! * (n+1)! * (n+2)! * 27^n);
(%i8)    AntiDifference(%, n);

\begin{align} (\%\o7)\qquad&\frac{(3n)!}{(n+1)^2(n+2)27^nn!^3}\\\\ (\%\o8)\qquad&\frac{9(81n^2+99n+20)(3n)!}{40(n+1)27^nn!^3} \end{align}

　またsimplify_sum(例2)と同様にpartfracによる部分分数分解によって結果が綺麗になる場合がありますが、AntiDifferenceやpartfracはsimplify_sumに比べ、文字の多い式や無理数の含まれた式を因数分解する力が弱いのかあんまりうまくいかない場合もあるので、そういう時はある程度手動で因数分解しておきましょう。

partfracの使用例

(%i1)    load(zeilberger)$
(%i2)    A: 1 / (n^2 + sqrt(5)*n - 1);
(%i3)    AntiDifference(A, n);
(%i4)    partfrac(%, n);

\begin{align} \mathrm{A}\qquad&\frac1{n^2+\sqrt5n-1}\\\\ (\%\o3)\qquad&\frac{\dis\frac{n^5}5+\frac{(\sqrt5+2)n^4}2+\frac{(6\sqrt5+8)n^3}3+\frac{(3\sqrt5+8)n^2}2-\farc{(3\c5^{\frac32}-32)n}{15}}{(n^2+\sqrt5n-1)(n^2+\sqrt5n+2n+\sqrt5)((n+1)^2+\sqrt5(n+1)+2(n+1)+\sqrt5)}\\\\ (\%\o4)\qquad& -\frac{(42-88\sqrt5)n-263\sqrt5-59}{96\c5^\frac32(n^2+(\sqrt5+4)n+2\sqrt5+3)} +\frac{-40n-13\sqrt5-40}{240(n^2+(\sqrt5+2)n+\sqrt5)} -\frac{(-88\sqrt5-42)n+87\sqrt5-143}{96\c5^\frac32(n^2+\sqrt5n-1)} \end{align}

(%i5)    A: 1 / ((n + sqrt(5)/2 + 3/2) * (n + sqrt(5)/2 - 3/2));
(%i6)    AntiDifference(A, n);
(%i7)    partfrac(%, n);

\begin{align} \mathrm{A}\qquad&\frac1{(n+\frac{\sqrt5}2-\frac32)(n+\frac{\sqrt5}2+\frac32)}\\\\ (\%\o6)\qquad&\frac{\dis4\l(-\frac{n^2}4-\frac{(\sqrt5-1)n}4+\frac{3\sqrt5-7}{24}\r)}{(n+\frac{\sqrt5}2-\frac32)(n+\frac{\sqrt5}2-\frac12)(n+\frac{\sqrt5}2+\frac12)}\\\\ (\%\o7)\qquad& -\frac2{3(2n+\sqrt5+1)}-\frac2{3(2n+\sqrt5-1)}-\frac2{3(2n+\sqrt5-3)} \end{align}

計算例と補足(Zeilberger)

二項係数の和

(%i1)    load(zeilberger)$
(%i2)    Zeilberger(binomial(n, k) * x^k, k, n);
(%i3)    Zeilberger(binomial(n, k) * y^n, n, k);

\begin{align} (\%\o2)\qquad&\l[\l[\frac k{n-k+1},\ [x+1,\ -1]\r]\r]\\ (\%\o3)\qquad&\l[\l[\frac{n-k}{k+1},\ [y,\ y-1]\r]\r] \end{align}

　これはつまり
$$F_1(n,k)=\binom nkx^k,\quad F_2(n,k)=\binom nky^n$$
に対し
\begin{align} G_1(n,k)&=\frac k{n-k+1}F_1(n,k)=\binom n{k-1}x^k\\ G_2(n,k)&=\phantom{{}+1}\frac{n-k}{k+1}F_2(n,k)=\binom n{k+1}y^n \end{align}
とおくと
\begin{align} (x+1)F_1(n,k)-\phantom{(y-1)}F_1(n+1,k)&=G_1(n,k+1)-G_1(n,k)\\ yF_2(n,k)+(y-1)F_2(n,k+1)&=G_2(n+1,k)-G_2(n,k) \end{align}
が成り立つことを意味しており、これによって
$$f_1(n)=\sum^n_{k=0}\binom nkx^k,\quad f_2(k)=\sum^\infty_{n=k}\binom nky^n$$
が漸化式
\begin{align} (x+1)f_1(n)-\phantom{(y-1)}f_1(n+1)&=0\\ yf_2(k)+(y-1)f_2(k+1)&=0 \end{align}
を満たすことがわかります。

Apéry数列

(%i1)    load(zeilberger)$
(%i2)    F(a) := binomial(n,k)^2 * binomial(n+k,k)^a;

$$(\%\o2)\qquad F(a):=\binom nk^2\binom{n+k}k^a$$

(%i3)    Zeilberger(F(1), k, n)[1][1];
(%i4)    Zeilberger(F(1), k, n)[1][2];

\begin{align} (\%\o3)\qquad& -\frac{k^3(n+1)(11n^2-6kn+37n-k^2-7k+30)}{(n-k+1)^2(n-k+2)^2}\\ (\%\o4)\qquad& [-(n+1)^2,\ -(11n^2+33n+25),\ (n+2)^2] \end{align}

(%i5)    Zeilberger(F(2), n, k)[1][1];
(%i6)    Zeilberger(F(2), n, k)[1][2];

\begin{align} (\%\o5)\qquad& \frac{4k^4(2n+3)(4n^2+12n-2k^2+3k+8)}{(n-k+1)^2(n-k+2)^2}\\ (\%\o6)\qquad& [-(n+1)^3,\ (2n+3)(17n^2+51n+39),\ {-}(n+2)^3] \end{align}

　これについても同様に Apéry数列
$$f_3(n)=\sum^n_{k=0}\binom nk^2\binom{n+k}k,\quad f_4(n)=\sum^n_{k=0}\binom nk^2\binom{n+k}k^2$$
が漸化式
\begin{align} -(n+1)^2f_3(n)-\phantom{(2n+3)}(11n^2+33n+25)f_3(n+1)+(n+2)^2f_3(n+2)&=0\\ -(n+1)^2f_4(n)+(2n+3)(17n^2+51n+39)f_3(n+1)-(n+2)^2f_4(n+2)&=0 \end{align}
を満たすことを意味しています。
　また有理関数$G(n,k)/F(n,k)$や漸化式の係数だけを出力させたい場合はこのようにZeilberger(F(n,k),k,n)[1][2]とリストのインデックスを指定しましょう(リストのインデックスは$1$から始まることに注意)。なおMAX_ORDまで計算して漸化式が求まらなかった場合はinvalid indexのエラーが出ることになります。

solve_recパッケージ

　最後に Petkovšek's algorithm を実行できるパッケージ：solve_recについて解説していきましょう。
　これを呼び出すためには予めload(solve_rec)というコマンドを実行しておく必要があります。
　このパッケージには主にsolve_rec, reduce_orderの2つのコマンドが用意されています。

solve_rec(rec,x[n])
数列$x_n$に関する多項式係数の線形漸化式$\mathrm{rec}$を与えたとき、その超幾何数列による一般解を返します。初期値を与えることで具体的な解を求めることもできます(後述)。
reduce_order(rec,y[n],x[n])
数列$x_n$に関する多項式係数の線形漸化式$\mathrm{rec}$とその解の一つ$x_n=y_n$を与えたとき
$$u_n=\frac{x_{n+1}}{y_{n+1}}-\frac{x_n}{y_n}$$
が満たす漸化式を返します。

計算例と補足

フィボナッチ数の一般項

(%i1)    load(solve_rec)$
(%i2)    rec: F[n+2] = F[n+1] + F[n]$
(%i3)    solve_rec(rec, F[n]);

$$(\%\o3)\qquad F_n=\frac{(\sqrt5-1)^n\%k_1(-1)^n}{2^n}+\frac{(\sqrt5+1)^n\%k_2}{2^n}$$

(%i4)    rec: F[n+2] - F[n+1] - F[n]$
(%i5)    solve_rec(rec, F[n], F[0]=0, F[1]=1);

$$(\%\o5)\qquad F_n=\frac{(\sqrt5+1)^n}{\sqrt5\c2^n}-\frac{(\sqrt5-1)^n(-1)^n}{\sqrt5\c2^n}$$

　(%o3)における$\%k_1$や$\%k_2$は任意の定数を意味しています。
　(%i4)のように$\mathrm{rec}$として = を含まない式を与えた場合は$\mathrm{rec}=0$という漸化式と解釈されます。
　(%i5)のように初期値を指定した場合は対応する$\%k_1$や$\%k_2$の値を求めてくれます。

出力について

(%i1)    load(solve_rec)$
(%i2)    rec: x[n+1] = (4*n+1) * ((n+1)^2+1) * x[n]$
(%i3)    solve_rec(rec, x[n]);

$$(\%\o3)\qquad x_n =\frac{\dis\%k_1\l(\prod^n_{\%j_1=1}(\%j_1^2+1)\r)4^n\G(n+\tfrac14)}{\G(\frac14)}$$

(%i4)    product_use_gamma: false;
(%i5)    solve_rec(rec, x[n]);

$$(\%\o5)\qquad x_n =\%k_1\prod^n_{\%j_1=1}(4\%j_1-3)\prod^n_{\%j_1=1}(\%j_1^2+1)$$

　このように漸化式の解が階乗などの単純な関数では表せない場合、solve_recはガンマ関数や総乗を用いて解を表そうとします。
　また漸化式の解をガンマ関数を含まない形に表したい場合はproduct_use_gammaにfalseを代入しておきましょう。

reduce_orderの使用例

(%i1)    load(solve_rec)$
(%i2)    rec: f[n+2] = (n+1) * (f[n+1] + f[n])$
(%i3)    solve_rec(rec, f[n]);
         WARNING: found some hypergeometrical solutions!

$$(\%\o5)\qquad f_n=\%k_1\c n!$$

(%i4)    reduce_order(rec, n!, f[n]);

\begin{align} (\%\mathrm{t}4)\qquad&f_n=\%z_n\c n!\\ (\%\mathrm{t}5)\qquad&\%z_n=\sum^{n-1}_{\%j=0}\%u_{\%j}\\ (\%\mathrm{o}5)\qquad&((-n-2)\%u_{n+1}-\%u_n)(n+1)! \end{align}

　これは漸化式
$$f_{n+2}=(n+1)(f_{n+1}+f_n)$$
の解の一つ$f_n=n!$を用いて
$$u_n=\frac{f_{n+1}}{(n+1)!}-\frac{f_n}{n!}$$
とおいたとき、これが
$$((-n-2)u_{n+1}-u_n)(n+1)!=0$$
を満たすことを意味しています。
　特にこの漸化式を解くことで
$$u_n=k_1\frac{(-1)^{n+1}}{(n+1)!}\quad(k_1\ \text{は任意})$$
つまり
\begin{align} f_n &=n!\l(\sum^{n-1}_{j=-1}u_j+k_2\r)\\ &=n!\l(k_1\sum^n_{j=0}\frac{(-1)^j}{j!}+k_2\r)\quad(k_1,k_2\ \text{は任意}) \end{align}
という一般解を得ることができます。

Riccati型の漸化式

(%i1)    load(solve_rec)$
(%i2)    rec: n*x[n+1]*x[n] - x[n+1]/(n+2) + x[n]/(n-1) = 0$
(%i3)    solve_rec(rec, x[n], x[3]=5);

$$(\%\o3)\qquad x_n=\frac{\frac{1584(-1)^{n+1}}{(n+1)(n+2)n!^2}-\frac{(n-1)n(n+3)(5(n+1)-3)(-1)^{n+1}}{n!^2}}{\frac{1584(-1)^n}{(n-1)!^2n(n+1)}-\frac{(n-2)(n-1)(n+2)(5n-3)(-1)^n}{(n-1)!^2}}+\frac n{n^3+n^2-2n}-\frac1{n^3+n^2-2n}$$

(%i4)    factor(ratsimp(minfactorial(factcomb(%))));

$$(\%\o4)\qquad x_n=-\frac{30(n-1)n(n+1)}{5n^6-3n^5-25n^4+15n^3+20n^2-12n-1584}$$

　ちなみにsolve_recでは線形方程式だけでなくRiccati型と呼ばれる
$$p(n)x_nx_{n+1}+q(n)x_{n+1}+r(n)x_n+s(n)=0$$
という形の非線形漸化式も解くことができます。これは
$$x_n=\frac{y_{n+1}}{y_n}-\frac{q(n)}{p(n)}$$
とおくことで$y_n$に関する線形漸化式
$$p(n)y_{n+2}+(q(n+1)+r(n))y_{n+1}+(q(n)r(n)+s(n))y_n=0$$
に帰着されます。
　特に上のように適当な初期値に対し$y_n$が超幾何数列として求まる場合、$x_n$は有理関数として求まることになりますが、その場合は上で紹介した簡約化のテンプレ

factor(ratsimp(minfactorial(factcomb( hoge ))))

を実行することで簡潔な表示を得ることができます。

おわりに

　以上がMaximaにおけるGosper, Zeilberger, Petkovšekのアルゴリズムの実行に関する概説でした。
　いやあ個人的に超幾何数列の記事を書き始めて一年くらい手計算だけで数式をこねくり回してきただけあって、Maximaに数式を突っ込んだら一瞬で計算が終わるというのは感慨深いものがありますね。
　とはいえMaximaにはまだ