logがある積分の解法まとめ

\begin{align} I&=\int_{0}^{1}x\log x dx \\&=\left[\frac{x^2}{2}\log x\right]^{1}_{0}-\frac{1}{2}\int_{0}^{1}xdx \\&=\frac{1}{2}\lim_{x\to0}x^2\log x-\frac{1}4 \\&=-\frac{1}{4} \end{align}
\begin{align} \lim_{x\to0}x^2\log x &=\lim_{x\to0}\frac{\log x}{\frac{1}{x^2}} \\&=\lim_{x\to0}\frac{\frac{1}{x}}{-\frac{2}{x^3 }} \\&=-\frac{1}{2}\lim_{x\to0}x^2 \\&=0 \end{align}

\begin{align} I&=\int_{1}^{e}\frac{\log x}{x}dx \\&=\int_{0}^{1}t\ dt\qquad(\log x\mapsto t) \\&=1 \end{align}

$$\log(1-x)=-\sum_{n=1}^{\infty}\frac{x^n}{n}\quad(|x|<1)$$
$$\log(1+x)=-\sum_{n=1}^{\infty}\frac{(-1)^n\ x^n}{n}\quad(|x|<1)$$
$$\log\left(2\sin\frac{x}{2}\right)=-\sum_{n=1}^{\infty}\frac{\cos nx}{n}\quad\left(0< x<\frac{\pi}{2}\right)$$
$$\log\left(2\cos\frac{x}{2}\right)=-\sum_{n=1}^{\infty}\frac{(-1)^n\ \cos nx}{n}\quad\left(0< x<\frac{\pi}{2}\right)$$
$$\log\tan\frac{x}{2}=-2\sum_{n=1}^{\infty}\frac{\cos(2n+1)x}{2n+1}\quad\left(0< x<\frac{\pi}{2}\right)$$

\begin{align} I&=\int_{0}^{1}\frac{\log(1+x)}{\sqrt{x}}dx \\&=-\int_{0}^{1}\sum_{n=1}^{\infty}\frac{(-1)^n\ x^n}{n\ \sqrt{x}}dx \\&=-\sum_{n=1}^{\infty}\frac{(-1)^n}{n}\int_{0}^{1}x^{n-\frac{1}{2}}\ dx \\&=-2\sum_{n=1}^{\infty}\frac{(-1)^n}{n(2n+1)} \\&=-2\left(\sum_{n=1}^{\infty}\frac{(-1)^n}{n}-2\sum_{n=1}^{\infty}\frac{(-1)^n}{2n+1}\right) \\&=-2\left(\log2+\frac{\pi}{2}-2\right) \\&=-2\log2-\pi+4 \end{align}

\begin{align} I&=\int_{0}^{\frac{\pi}{2}}\log\left(2\sin\frac{x}{2}\right)\log\left(2\cos\frac{x}{2}\right)dx \\&=\frac{1}{2}\int_{0}^{\pi}\log\left(2\sin\frac{x}{2}\right)\log\left(2\cos\frac{x}{2}\right)dx \\&=\frac{1}{2}\sum_{n,m>0}\frac{(-1)^n}{nm}\int_{0}^{\pi}\cos mx\cos nx dx \\&=\frac{\pi}{4}\sum_{n=1}^{\infty}\frac{(-1)^n}{n^2} \\&=-\frac{\pi^3}{48} \end{align}

\begin{align} I&=\int_{0}^{\infty}e^{-x}\log xdx \\&=\left.\frac{d}{ds}\int_{0}^{\infty}x^s e^{-x}dx\right|_{s=1} \\&=\Gamma'(1) \\&=\Gamma(1)\psi(1) \\&=-\gamma \end{align}

$$I=\int_{0}^{1}\frac{x^2-x}{\log x}dx$$
$$f(t)=\int_{0}^{1}\frac{x^t}{\log x}$$
\begin{align} f'(t)&=\int_{0}^{1}x^t \\&=\frac{1}{t+1} \end{align}
\begin{align} f(2)-f(1)&=\int_{1}^{2}f'(t)dt \\&=\int_{1}^{2}\frac{1}{t+1}dt \\&=\log\frac{3}{2} \end{align}

$$I=\int_{0}^{\infty}\frac{x\log x}{x^4+1}dx$$
$$f(z)=\frac{z\log z}{z^4+1}$$
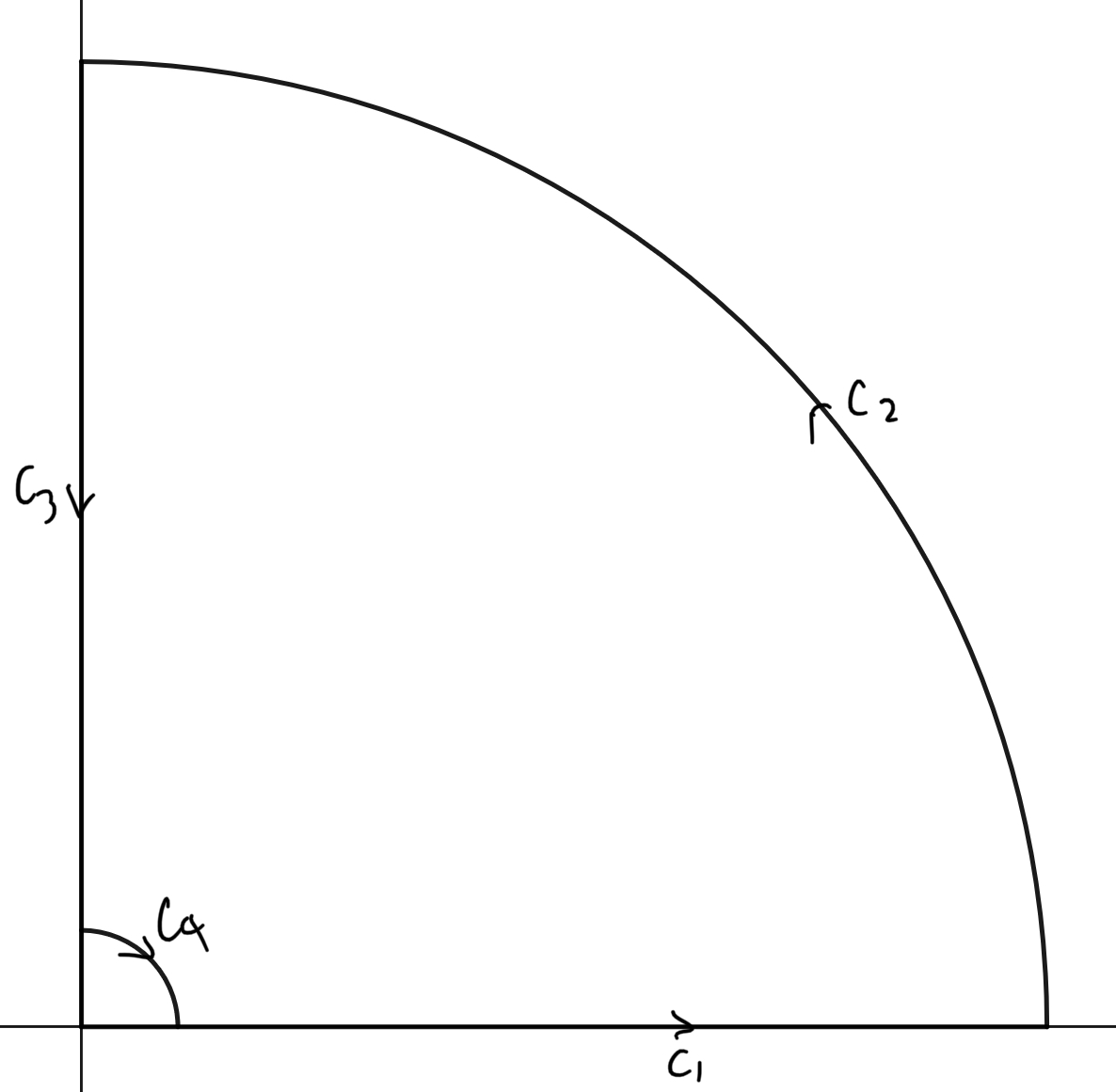積分経路
$\log0$を回避するために$0$は避けています。
$\displaystyle C_2,C_4$は評価して極限とばすと$0$になります。
確認してみてください。
全体の積分を$C$としておきます。
それぞれ計算していきます。

\begin{align} \int_{C_1}&=\int_{\varepsilon}^{R}f(z)dz \\&=I\qquad(\ip\to0,R\to\infty) \end{align}
\begin{align} \int_{C_3}&=\int_{iR}^{i\ip}f(z)dz \\&=-i\int_{\ip}^{R}f(ix)dx \\&=\int_{\ip}^{R}\frac{x\log ix}{x^4+1}dx \\&=\int_{\ip}^{R}\frac{x\log x}{x^4+1}dx+\frac{i\pi}{2}\int_{\ip}^{R}\frac{x}{x^4+1}dx \\&=I+\frac{\pi^2}{8}i\qquad(\ip\to0,R\to\infty) \end{align}
\begin{align} \oint_{C}&=2\pi i\underset{z=e^{\frac{i\pi}{4}}}{\mathrm{Res}}\frac{z\log z}{z^4+1} \\&=2\pi i\lim_{z\to e^{\frac{i\pi}{4}}}\frac{z\log z(z-e^{\frac{i\pi}{4}})}{z^4+1} \\&=2\pi i\lim_{z\to e^{\frac{i\pi}{4}}}\frac{(2z-e^{\frac{i\pi}{4}})\log z-e^{\frac{i\pi}{4}}+z}{4z^3} \\&=\frac{\pi^2}{8}i \end{align}
$$\oint_{C}=\int_{C_{1}}+\int_{C_{2}}+\int_{C_{3}}+\int_{C_{4}}$$
$$\frac{\pi^2}{8}i=I+I+\frac{\pi^2}{8}i$$
$$I=0$$