のぞき見！結び目理論／第一回「定義」

はじめに

本稿は結び目理論のおいしいところを一般の方へ即席で伝えることをコンセプトにしたシリーズです．よって，専門知識は問いませんし，証明も省略します．分野名だけ知っている人がどんな感じなのか参照したり，何も知らない人が興味を持つきっかけになったりすれば目的を十分に果たしたと言えます．数学科の学生などでしっかり学びたいという方はしかるべき順を追うようにしてください．

シリーズは以下の全六回です．
第一回「定義」
第二回「表示」
第三回「同値」
第四回「不変量」
第五回「ジョーンズ多項式(1)」
第六回「ジョーンズ多項式(2)」

結び目は約28,000年前の縄が出土していることからもわかる通り，有史以前から装飾目的や実用目的で文化として人類が慣れ親しんできたものです．一方，本格的に数学の研究対象になったのは1870年代のことであり，きっかけはケルビン卿として知られる物理学者トムソンが当時存在すると信じられていたエーテルの渦(これを原子の正体と考えていた)について友人の数学者テイトに相談したこととされます．その発祥エピソードを一例として理論物理と相性が良く，特に位相的場の理論とは互いに研究を加速させることになりました．

ただし関連のない自然科学分野の方が珍しく，純粋数学では代数的トポロジーはもちろん微分トポロジー，作用素環論，可積分系，表現論，さらには数論に至るまで幅広く，結び目構造は可解模型，高分子，DNA，地震曲線など意外なものにも多く現れます．

定義

まず，数学で扱う結び目のイメージはズバリ「$1$本の紐を結んで両端をつなげたもの」です．日常生活で結び目と言うと例えば下図中央のようなものを想像するかもしれません．しかし，$2$つの結び目がとある変形で移り合うかをこれから見ていきたいので，端を固定していないとどれもスルスルとほどけてしまってつまらないことになります．よってこのような条件を加えています．
注） 充電コードも両端を固定していれば絡まらないわけですね．

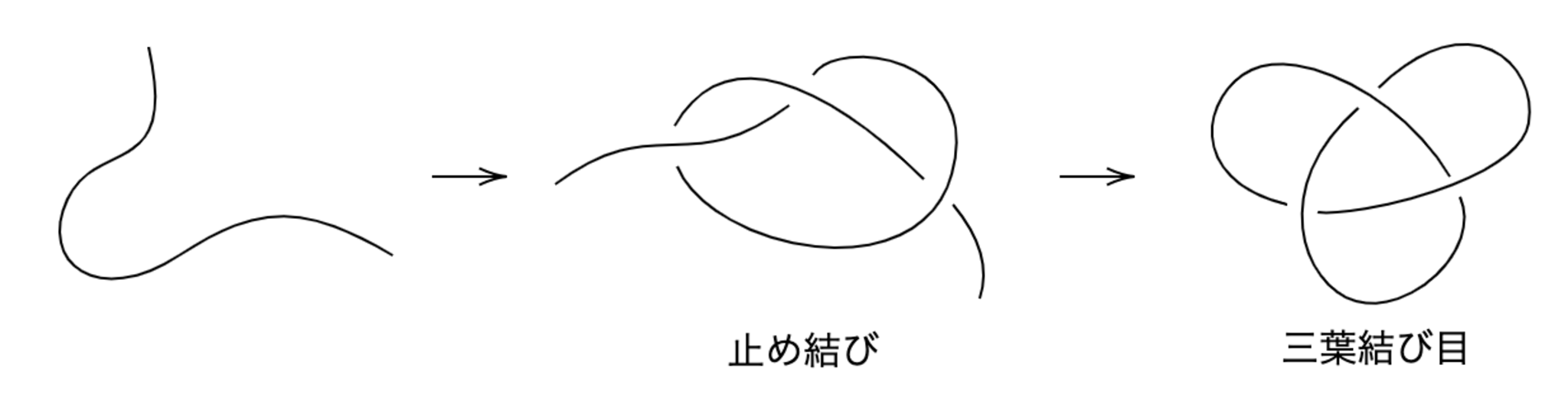
もう少しきちんとした定義を書いておきましょう．

注) 空間とは通常の$3$次元ユークリッド空間のことです．また，絡み目にはいくつかの向きの付け方があります．結び目なら(高々)$2$通りです．

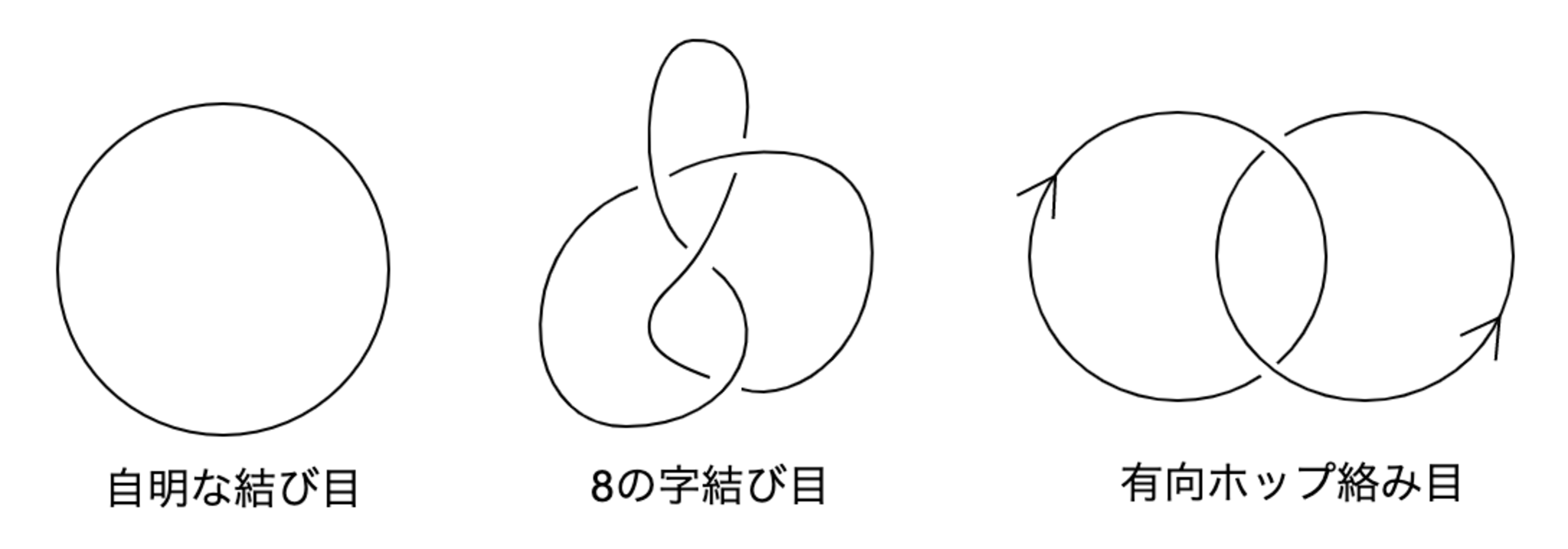
これで考察の対象が明確になりました．あとの展開のために追加で定義したものもありますが，ひとまず例を見ることにしましょう．ここにあるもの以外では，
ホワイトヘッド絡み目やボロミアン絡み目が歴史的には挙げられるほか，トーラス結び目やプレッツェル結び目といった系列がよく名前をつけられて研究されています．

さて，ここから結び目理論は何をしたいのかという点ですが，

• ある結び目が"ほどける"か
• $2$つの結び目が"同じ"であるか

が大きな問題意識です．叶うなら結び目の完全な分類を得たいのです．そのためには結び目が「同じ」であるとはどういうことか，基準を定めなくてはいけません．これは第三回で与えようと思います．