3
大学数学基礎解説
のぞき見!結び目理論/第二回「表示」
357
0
$$$$
【シリーズ一覧】
第一回「定義」
第二回「表示」
第三回「同値」
第四回「不変量」
第五回「ジョーンズ多項式(1)」
第六回「ジョーンズ多項式(2)」
表示
結び目をどのように紙上で描画し扱えばよいかを考えます.とはいえ,その方法は初回で既に実践しているので,ここで改めて紹介しましょう.以降,結び目に対し定義しますが,絡み目や有向の場合でも同様に定義されますし定理もそのまま置き換えたものが従います.
射影図
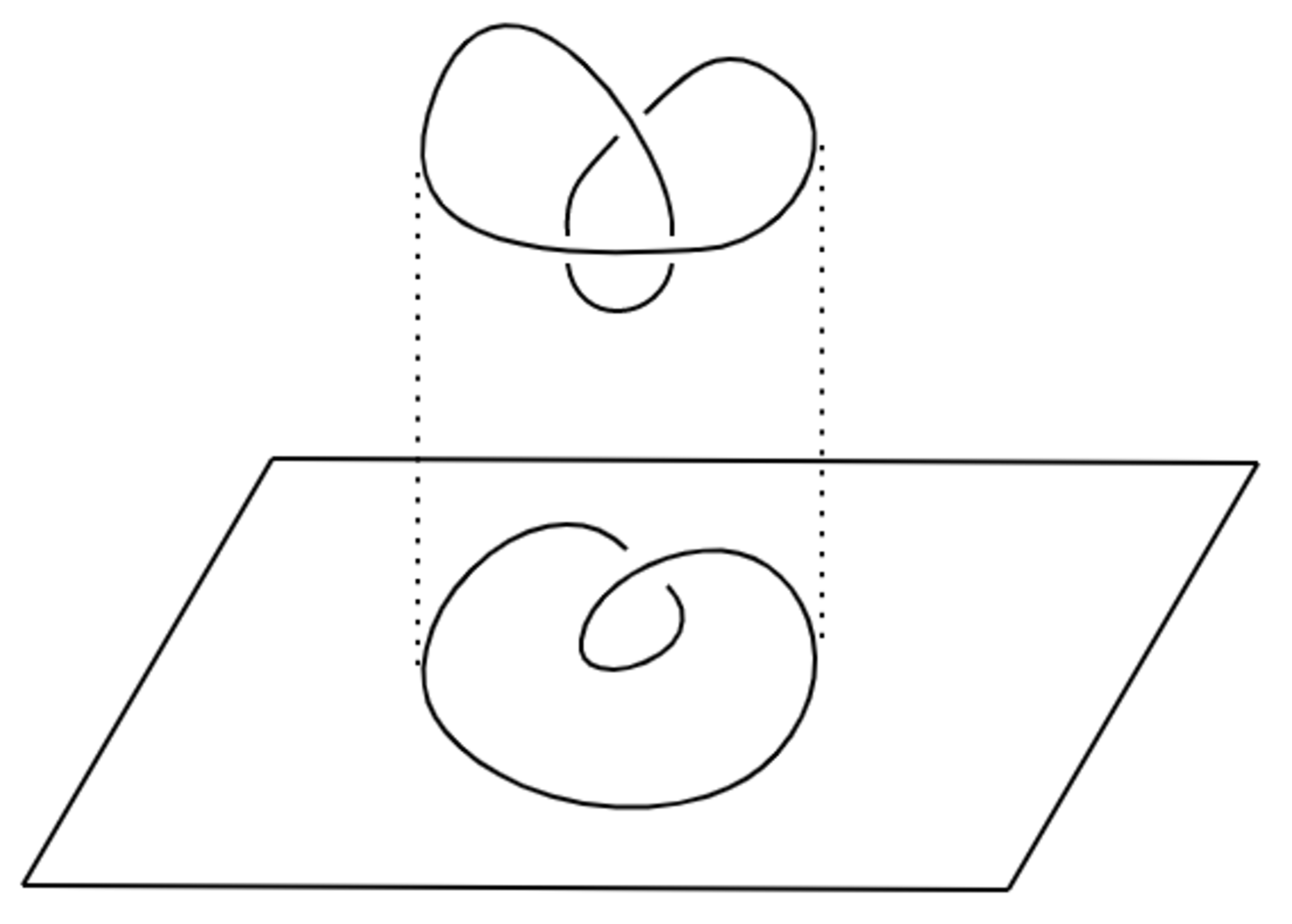
結び目をある平面上に射影して得られる図式を結び目の射影図という.
特に,次のような点を含まない射影図を正則であるという.
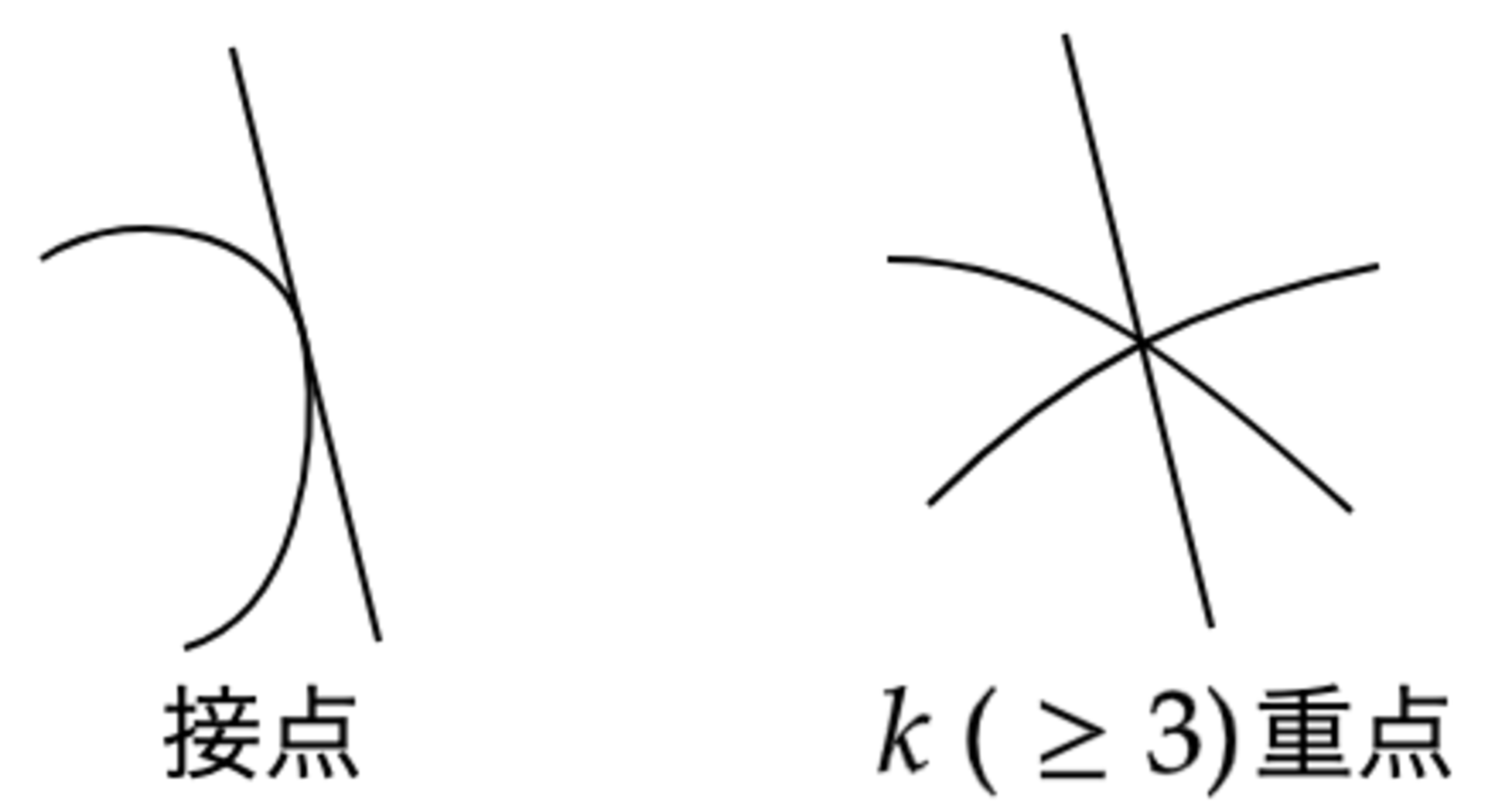
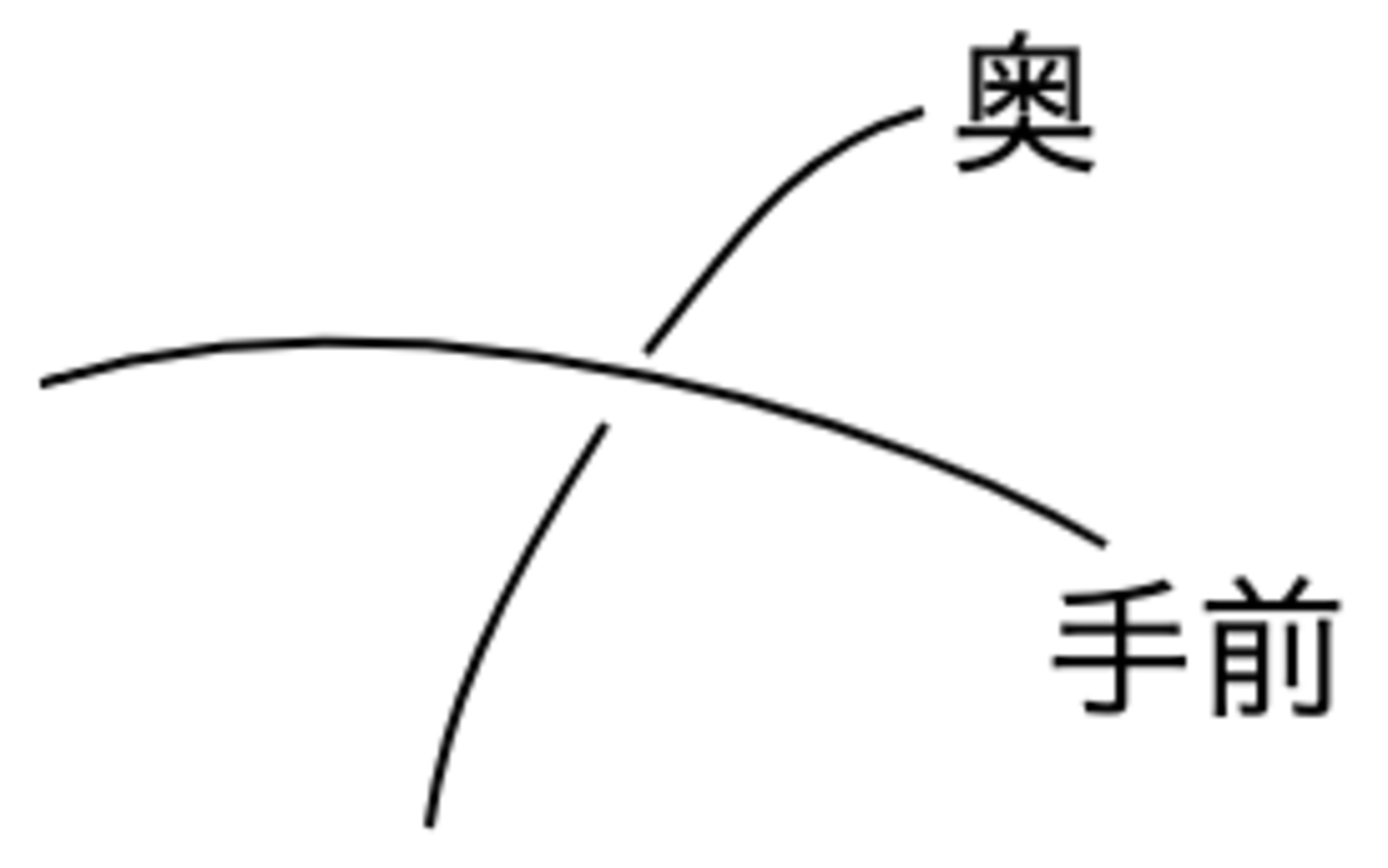
また,正則な図式において$2$重になった交点は上下関係を区別してかく.
注) 野生的な結び目と呼ばれる,射影図が交点を無限個もつような結び目は結び目理論では除外して考えることが一般的です.より正確には,有限個の線分からなる折れ線で実現できるもののみを扱います.これは感覚的には「太さをもてる」結び目であるということです.
たとえ禁止されている点を図式に含んだとしても,平面を少し傾ければずらすことができます.すなわち,以下の主張が成り立ちます.
全ての結び目は正則表示をもつ.すなわち,ある正則な射影図で表示できる.
これで結び目を表す適切な図式を定めることができました.ただし同一の結び目から似ても似つかない射影図が得られることがあるので注意が必要です.このあたりの対応は次回で述べます.
投稿日:2021年6月15日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中