のぞき見!結び目理論/第三回「同値」
【シリーズ一覧】
第一回「定義」
第二回「表示」
第三回「同値」
第四回「不変量」
第五回「ジョーンズ多項式(1)」
第六回「ジョーンズ多項式(2)」
同値
$2$つの結び目が「同じ」であるとはどういうことかが懸案の一つでした.早速ですがその定義から入りましょう.
$2$つの結び目が,切ることのない連続変形(全同位変形という)によって移り合うとき,同値であるという.
この全同位変形は例えばゴムひもの伸び縮みを想像してください.すると結び目の同値は素直に感覚を反映したものと言えるでしょう.このような結び目の同値性は図形の分類基準としての要請を満たしたもの(同値関係という)になっています.初回の問題意識に照らせば,結び目がほどけるとは自明な結び目と同値であることと解釈すればよさそうです.以降は結び目と言ったら同値なものは同一視することにしましょう.

さて,ここで前回扱った正則射影図による結び目の表示と絡めて,結び目の同値性の大変に有用な言い換えを与えようと思います.そのためにまずは次のような射影図の変形を考えます.
結び目の正則射影図に対し,次の局所変形RI〜RIIIをライデマイスター移動という.ただし,点線の円の外側は変えないものとする.
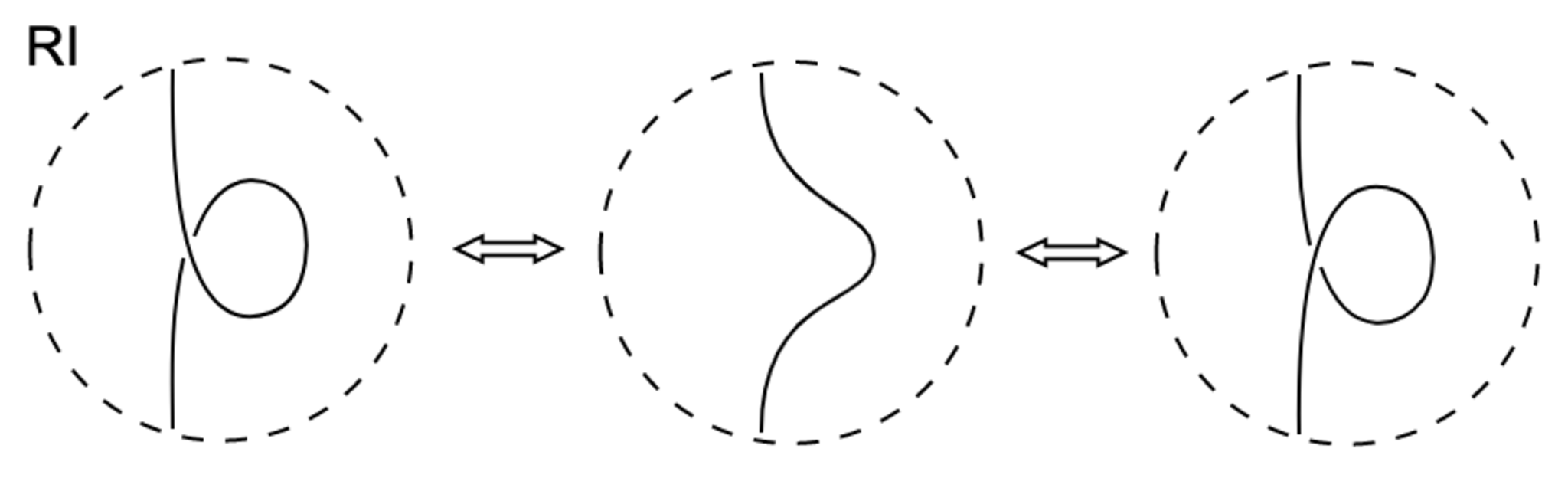
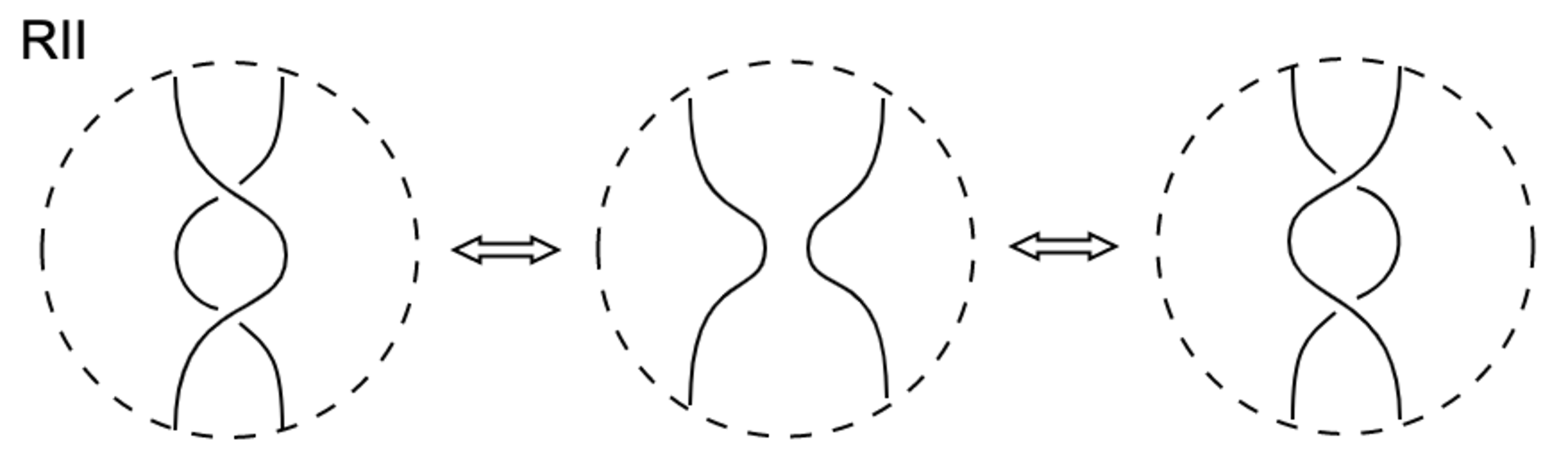
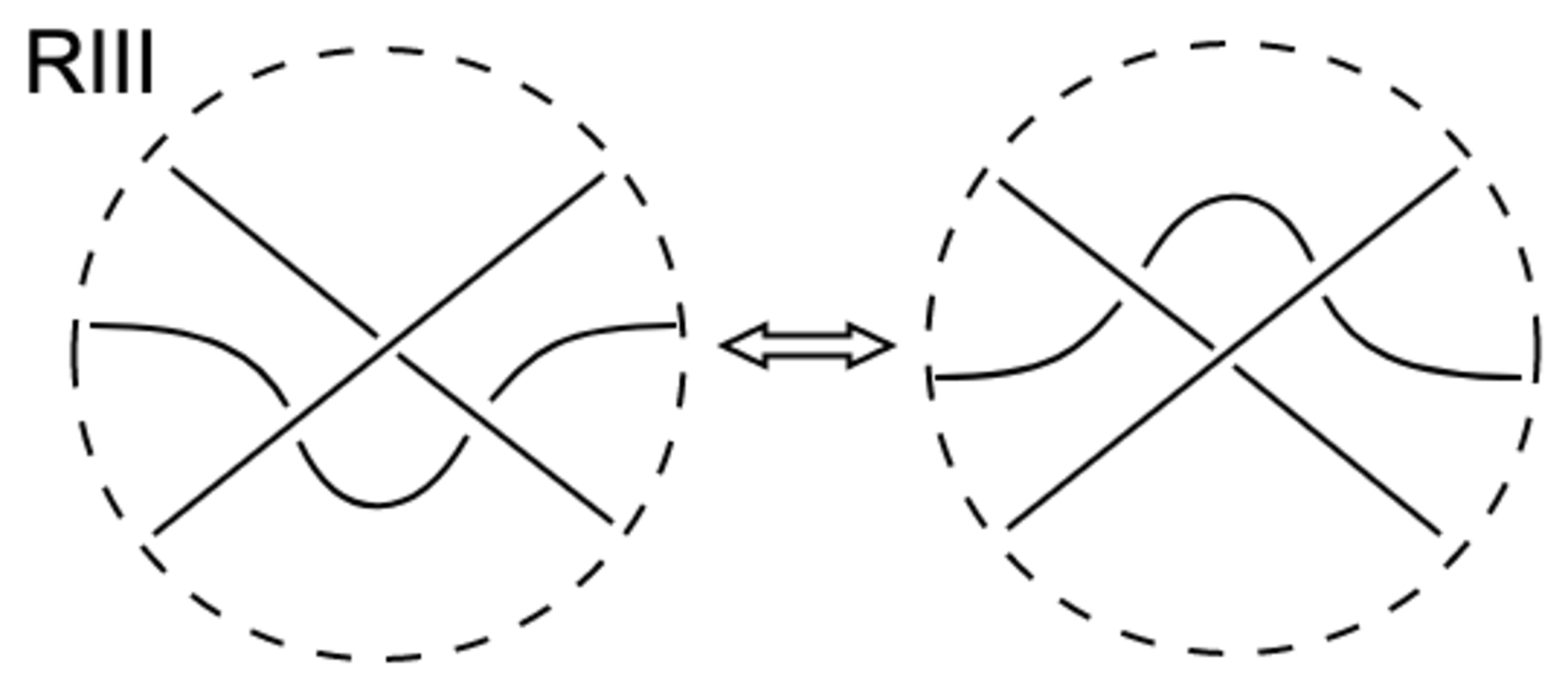
この$3$つはどこから湧いてきたのか,ピンとこない方が多いと思いますが,例えばRIIとRIIIは正則な射影図で禁止されていた接点と$3$重点を変形の"過程"に含むことがわかります.RIもある種の特異点が"過程"に含まれます.
ライデマイスター移動に関して,次の重要な定理が成り立ちます.
$2$つの結び目$K,K'$に対して
$K,K'$は同値
$ \Longleftrightarrow$$K,K'$の正則射影図は有限回のライデマイスター移動(と各断片の伸縮)によって移り合う.
注) 標準的な証明は各変形の軌跡が作る曲面に対し三角形分割を行います.
つまり,ライデマイスター移動による違いを同一視した正則射影図と結び目に$1$対$1$の対応があることがわかります.この事実は,我々が結び目理論を射影図のお絵かきによって展開できることを示唆しています.ちなみにライデマイスター移動RI〜RIIIは過不足ないことも示されています.すなわち,どのライデマイスター移動も他のライデマイスター移動の有限回の組み合わせでは実現できません.