のぞき見！結び目理論／第六回(終)「ジョーンズ多項式(2)」

【シリーズ一覧】
第一回「定義」
第二回「表示」
第三回「同値」
第四回「不変量」
第五回「ジョーンズ多項式(1)」
第六回「ジョーンズ多項式(2)」

ジョーンズ多項式(続き)

ジョーンズ多項式はスケイン関係式から本当に全ての有向絡み目に対して計算できるのか，特にスケイン分解樹が有限回で自明な結び目にたどり着いてくれるのか考えましょう．

このような性質をもつ操作を結び目解消操作といい，ある結び目を表す正則射影図に対してほどくために必要な結び目解消操作の回数の最小値を結び目解消数といってこれは結び目の不変量になります．余談ですが，全ての結び目は$4$次元空間内の変形ではほどけてしまうので，曲面結び目という高次元版も活発に考察されています．

さて，本題に戻ります．定理の証明はそれほど難しくありません．概略を述べましょう．射影図のある点から出発して結び目をたどることを考え，初めて通る交点は上を，既に通ったことのある交点は下を通るように上下を交換していけば(どんどん潜っていく形になって)ほどけるようになります．これをきちんと書けば証明になります．

ここでスケイン分解樹を考えると，上記の事実及び平滑化すれば交点数が$1$減ることから交点数についての帰納法が回ってジョーンズ多項式は有限回の手続きで計算可能であると証明できました．

この話題に関連して，交代結び目というクラスも紹介しておきます．射影図のある点からたどっていくとき，交点の上下を交互に通過するような図式を交代図式といい，交代図式をもつ結び目を交代結び目といいます．

"むすび"に

発展的な話題を少し．今ではジョーンズ多項式は量子不変量の一つとして理解されており，一般の量子不変量は統計物理に現れるヤン・バクスター方程式の解であるR行列から統一的に得られます．また，リー群やリー環の一般化であり神保とドリンフェルトにより導入された量子群の表現からも計算され，ジョーンズ多項式は特殊線形群$SL_2(\mathbb{C})$の表現に対応しているほか，共形場理論に現れるKZ方程式や配置空間とも密接に関連します．

さらに，ジョーンズ多項式において変数を$t=e^h$として$h$に関する冪級数展開を施したときの各係数はヴァシリエフの有限型不変量(有限回の"微分"で$0$になるため)という重要なクラスの不変量です．そして，それらの情報を併せ持ち反復積分で定義されるコンツェヴィッチの普遍量子不変量は完全不変量ではないかと期待されています．

最後に整数と結び目の関連を述べましょう．そのために結び目の連結和を定義します．

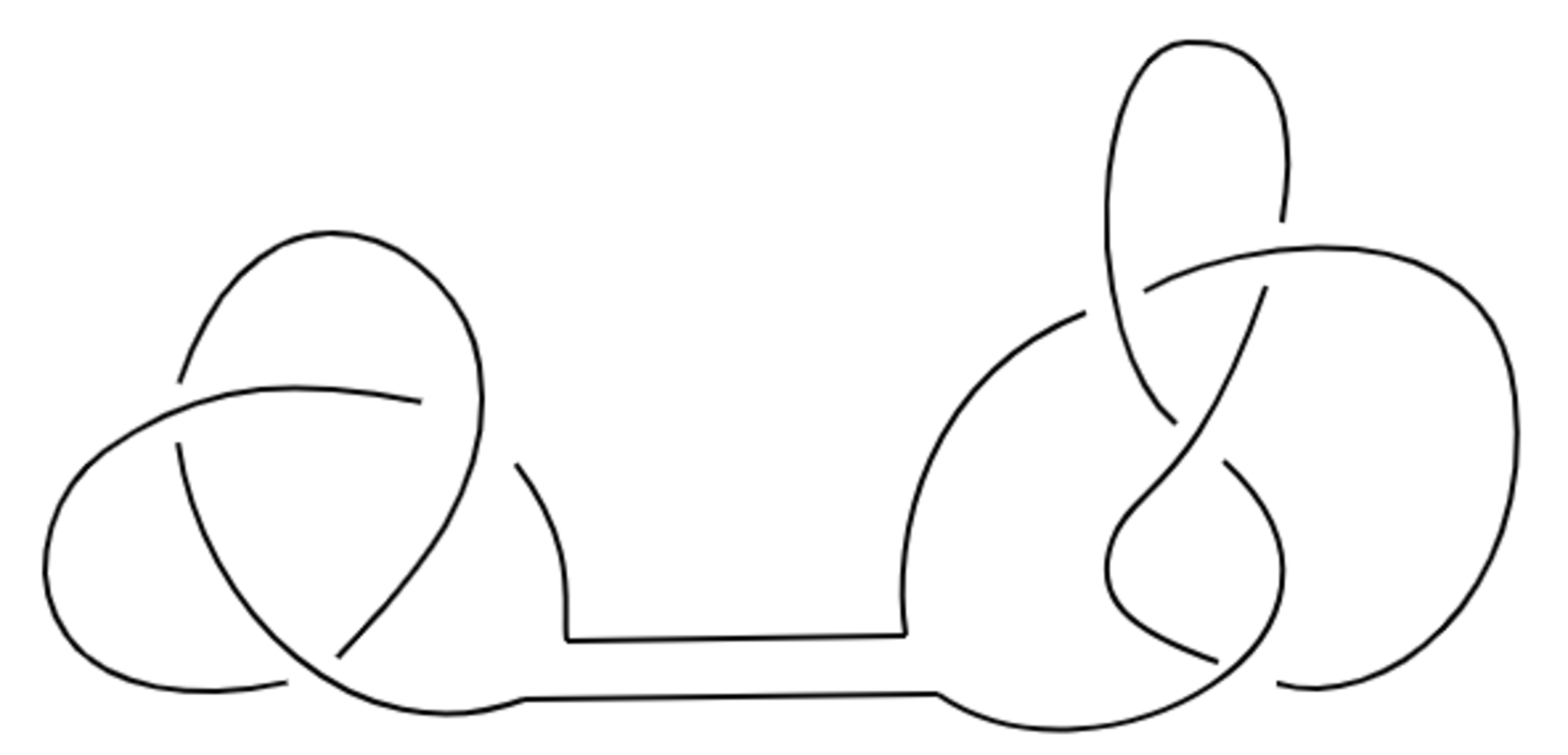
すると，"素因数分解の一意性"が結び目についても成り立つのです．

ちなみに，連結和に対してジョーンズ多項式は
$$V_{K\sharp K'}(t)=V_K(t)V_{K'}(t)$$
と振る舞ってくれます．

先人たちの尽力で明らかになりつつある結び目の分類表は最小交点数の小さい順に素な結び目(ただし鏡像は同一視)が並べられています．最小交点数$16$以下については分類を終えていて，ここまでで1,702,936種類もあるそうです．

本シリーズでは分野に入門する冒頭部分を解説しました．非常に図が豊富で視覚的に楽しいけれど同値の判定などでは視覚があてにならなくなる，そんな不思議で奥が深い結び目理論を少しでものぞき見ることはできたでしょうか．双曲幾何との関連から生じた体積予想など，数学者を悩ませる重要な未解決問題も多くあるのでまだまだ発展していくことでしょう．さらに知りたい項目がある方はぜひ書店や図書館で結び目理論のコーナーを見てみてくださいね．

ここまでお付き合いいただきありがとうございました！ついでに他の記事もどうぞ笑