のぞき見!結び目理論/第五回「ジョーンズ多項式(1)」
【シリーズ一覧】
第一回「定義」
第二回「表示」
第三回「同値」
第四回「不変量」
第五回「ジョーンズ多項式(1)」
第六回「ジョーンズ多項式(2)」
ジョーンズ多項式
ジョーンズは作用素環論という解析学の一分野の研究者であり,今回扱うジョーンズ多項式もその文脈で組みひも群の表現から発見されました.当時のトポロジストたちに衝撃を与える斬新な不変量で,これを契機として新たな不変量が大量に発見され量子トポロジーという新たな分野が花開きました.いよいよ結び目理論のおいしいところです.
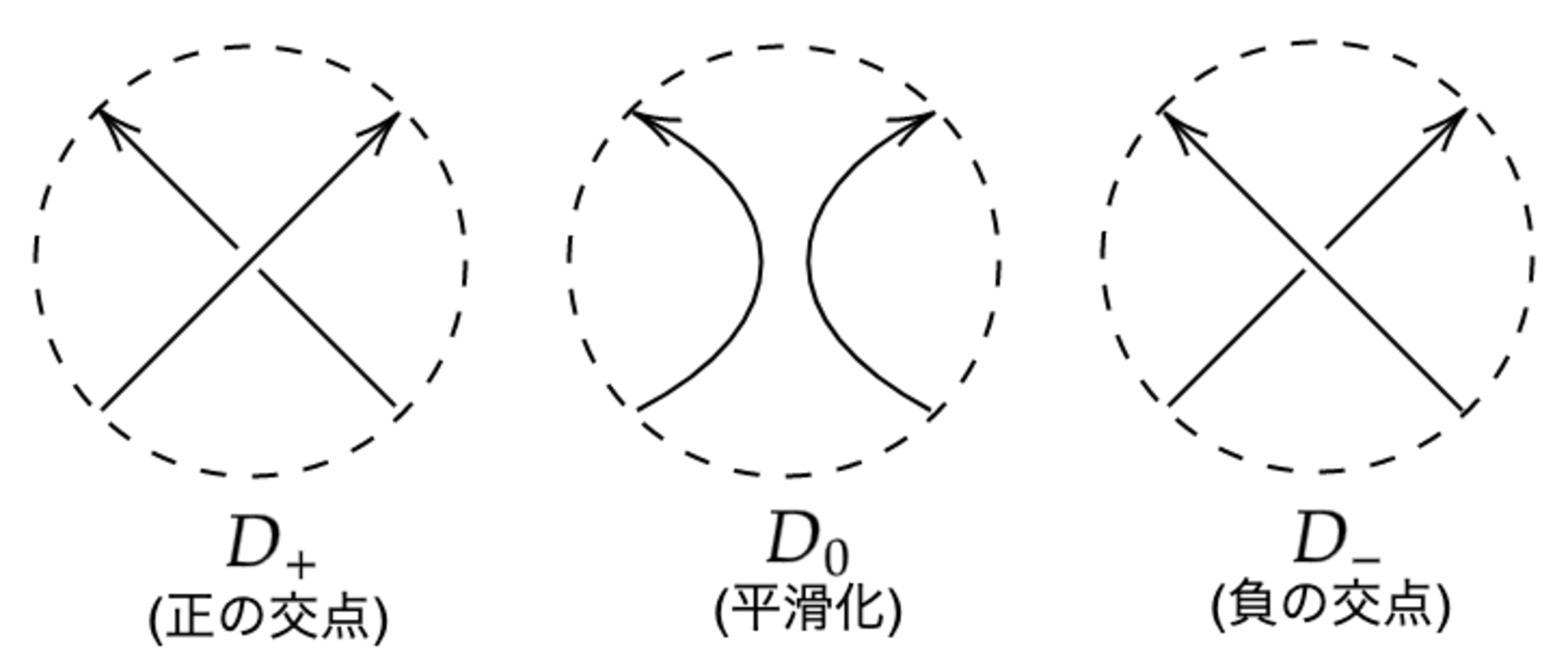
ジョーンズ多項式は有向絡み目の正則射影図$D$に対し以下の条件で帰納的に定義される.
- $V_○(t)=1$ (○は自明な結び目の交点を持たない射影図)
- $t^{-1}V_{D_+}(t)-tV_{D_-}(t)=(t^\frac{1}{2}-t^{-\frac{1}{2}})V_{D_0}(t)$ (コンウェイのスケイン関係式)
ただし,$D_+,D_0,D_-$はある一つの交点まわりで次のように異なっている図式であり,円の外部は同一である.
負冪も許すので正しくは$t^\frac{1}{2}$を変数とする整数係数「ローラン」多項式ということになります.なお,結び目など成分数が奇数の絡み目なら半整数乗は最終的には必要ありません.このように定義されたジョーンズ多項式は結び目の不変量です.
ジョーンズ多項式は射影図のライデマイスター移動に対して不変であり,どの有向絡み目に対してもただ一つ存在する.すなわち結び目の不変量である.また,結び目であれば向きの付け方によらずに定まる.
ジョーンズ多項式の同値な定義は複数あり,例えば状態和(分配関数)を用いた定義では数学者の気になる「存在と一意性」やライデマイスター不変性を比較的容易に確かめられます.ですが,今回は計算がしやすいスケイン関係式による定義を採用しました.前回言及したアレクサンダー多項式も係数の変えたスケイン関係式から得ることができ,それらの一般化であるホンフリー多項式というものもあります.
・アレクサンダー多項式$\nabla_{D}(z)$
$$\nabla_{D_+}(z)-\nabla_{D_-}(z)=z\nabla_{D_0}(z)$$
・ホンフリー多項式$P_{D}(a,x)$
$$a^{-1}P_{D_+}(a,x)-aP_{D_-}(a,x)=xP_{D_0}(a,x)$$
準備のためにまずは自明な結び目の分離和(射影図の各成分が交わらない)のジョーンズ多項式を計算します.成分数$2$の場合は下図を利用します.
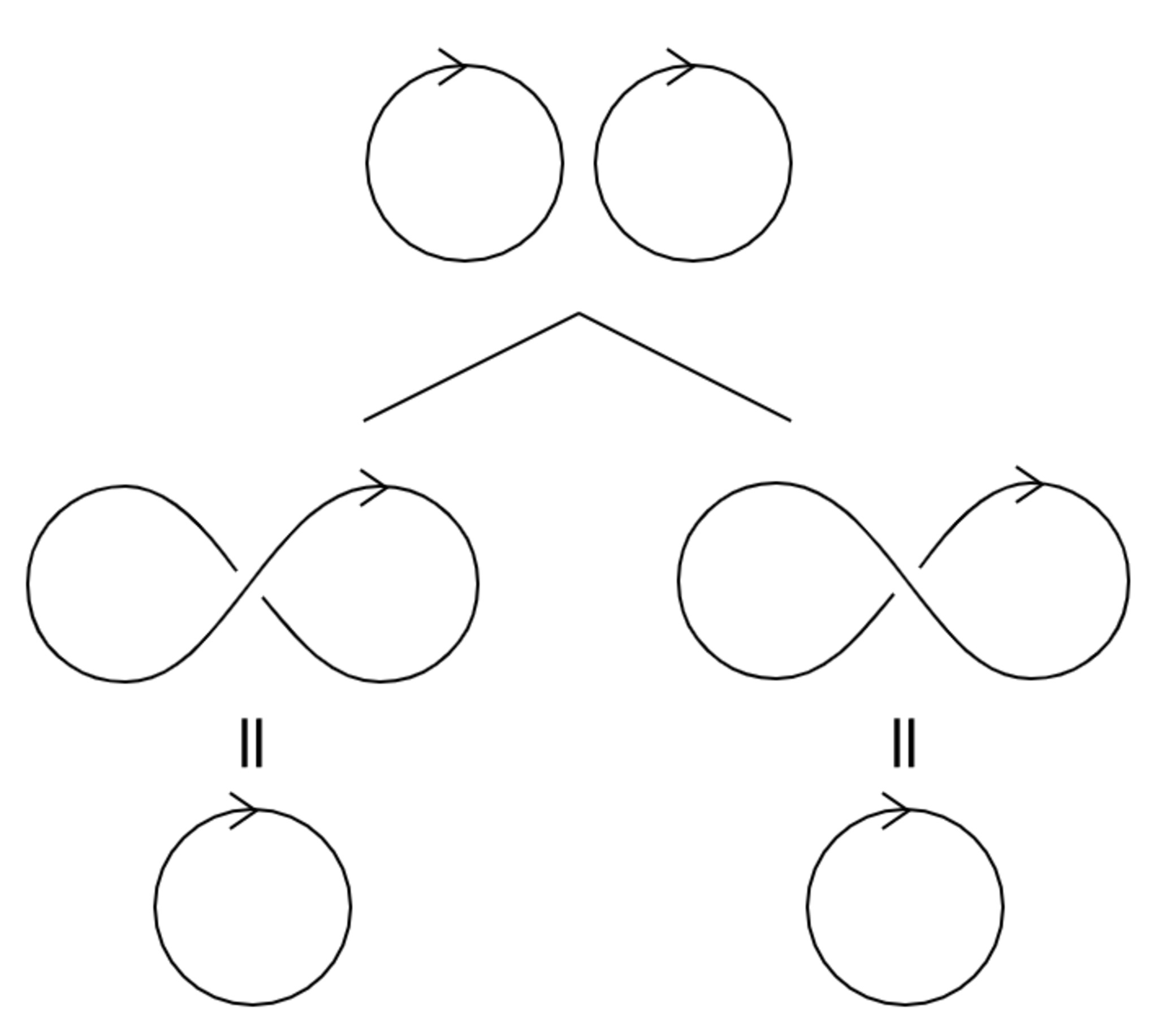
それぞれが正負の交点と平滑化に対応しているので,スケイン関係式から
$$(t^\frac{1}{2}-t^{-\frac{1}{2}})V_{○○}(t)=t^{-1}V_{○}(t)-tV_{○}(t)=t^{-1}-t$$
よって$V_{○○}(t)=-t^\frac{1}{2}-t^{-\frac{1}{2}}$です.
同様にして成分数が$k$のときは$V_{○^k}(t)=(-t^\frac{1}{2}-t^{-\frac{1}{2}})^{k-1}$です.
次は最も簡単な非自明結び目である三葉結び目でやってみます.
一つ交点を選びスケイン関係式が利用できるようにかき換えていくことを繰り返して樹形図を作ります(スケイン分解樹と呼ぶ).
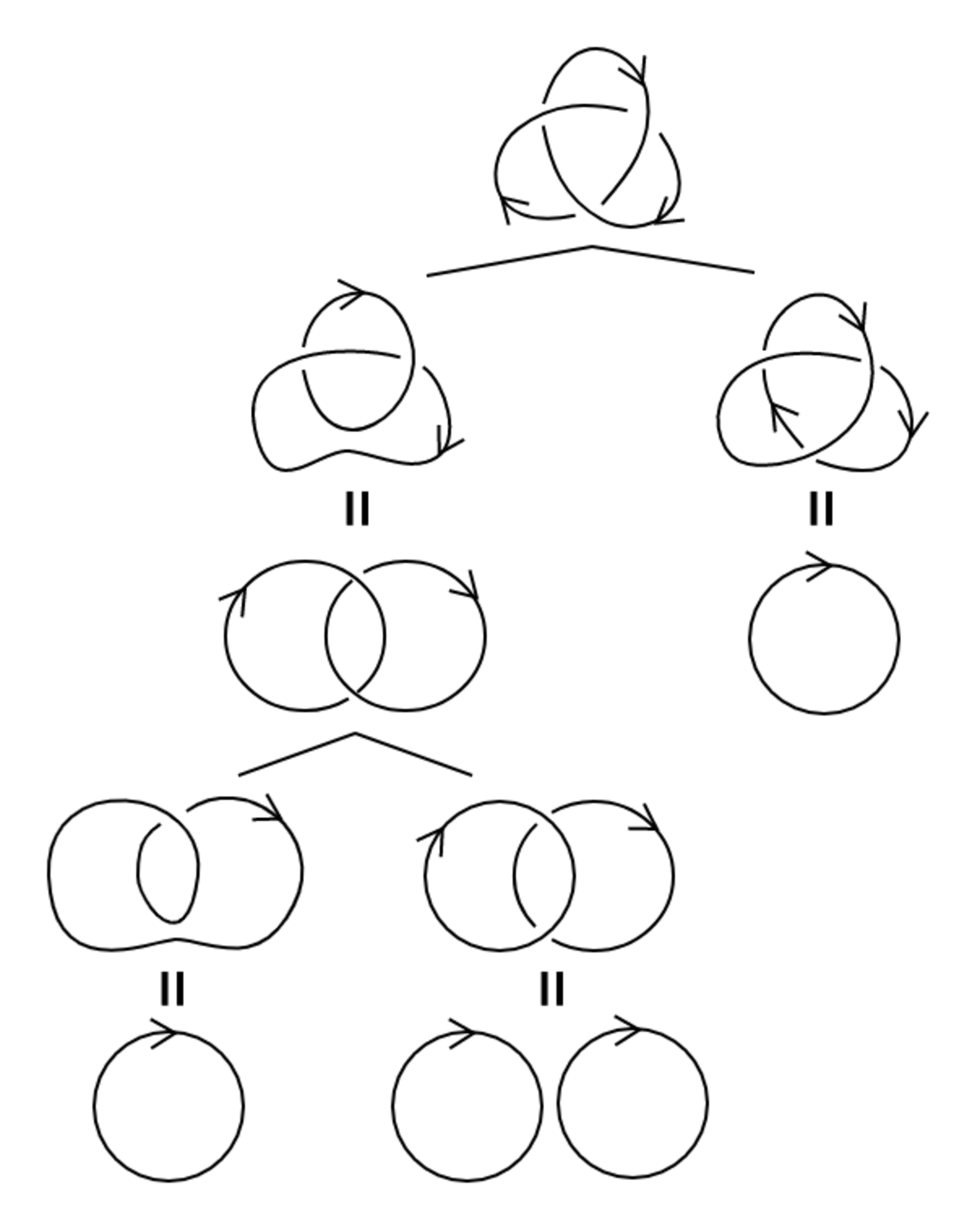
それぞれの末端の自明な絡み目から上に向けて関係式を使っていけば$V_{3_1}(t)=t+t^3-t^4$となります.
それでは,ジョーンズ多項式が両手型であるか,すなわち自身とその鏡像が同値であるか考えましょう.鏡像に関してもう一度スケイン分解樹をかいても良いですが,ここはジョーンズ多項式の一般的性質を使いましょう.結び目の射影図の鏡像をとるとき,交点の上下関係を全て逆にすればよいですね.よって定義式から
$$V_{\overline{D}}(t)=V_{D}(t^{-1})$$
となります.ところで,三葉結び目のジョーンズ多項式を見ると$V_{3_1}(t^{-1})=t^{-1}+t^{-3}-t^{-4}\neq V_{3_1}(t)$でしたから,両手型ではないと結論できました.本シリーズで三葉結び目と呼んでいるのは右手系(+)です.ちなみに,アレクサンダー多項式では鏡像の区別ができないことが定義式からわかります.
そんなジョーンズ多項式でも可逆性,すなわち結び目に対する$2$通りの向きの入れ方についてそれらが同値な有向結び目になるかの判定はできません.これは定理1から従うことです.時間のある方は三葉結び目が可逆であることを具体的な変形を見つけることで示してみてください.
加えて,どのような多項式ならそれをジョーンズ多項式とするような有向絡み目が存在するかの特徴づけも明らかになっていません.もちろんすぐにわかる必要条件もあり,$\omega$を$1$の$3$乗根($1$そのものでもよい)とすると全てのジョーンズ多項式について$V_K(\omega)=1$です.証明は読者への演習問題としておきます.これに関して,アレクサンダー多項式の方は$f(1)=\pm 1$かつ係数が対称な多項式$f$であることという特徴づけが知られています.