リーマン予想による素数定理の精密化
はじめに
この記事では
リーマン予想の記事
において紹介した
『リーマン予想が真$\iff|\pi(x)-\mathrm{Li}(x)|< C\sqrt x\log x\quad(x\gg0)$』
という関係において、この右側の主張を具体的に
$$|\pi(x)-\mathrm{Li}(x)|<\frac1{8\pi}\sqrt x\log x\quad(x\geq2657)$$
と評価できることを示します。ついでにこの不等式は
$$|\psi(x)-x|<\frac1{8\pi}\sqrt x\log^2x\quad(x\geq73.2)$$
や
$$|\vt(x)-x|<\frac1{8\pi}\sqrt x\log^2x\quad(x\geq599)$$
という不等式に置き換えられることも(暗に)示されます。
用語について
この記事では前の記事で使っていない記法やここでしか使われない表記がいくつかあるのでそれらについてまず触れておきます。
・$\rho,\b,\g$
特筆がなければ基本的に$\rho=\b+i\g$はそれぞれリーマンゼータ関数の非自明な零点とその実部、虚部を表わすものとします。特に総和記号$\sum$の下に$\g$についての条件が現れるときは$\g$が条件を満たすように$\rho$が動くものとします(これは一般的な記法です)。
・$N(T),F(T),R(T)$
$N(T)$は
前の記事
と同じく
$$N(T)=\sum_{0<\g\leq T}1$$
とし、$F(T),R(T)$については
\begin{align}
F(T)&=\frac T{2\pi}\log\frac T{2\pi}-\frac T{2\pi}+\frac78\\\\
R(T)&=0.137\log T+0.443\log\log T+1.588
\end{align}
と定めます(これはここだけの表記となります(多分))。
前の記事
では
$$N(T)=F(T)+O(\log T)$$
が成り立つことを示しましたが、より精密には
$$|N(T)-F(T)|\leq R(T)\quad(T\geq2)$$
が成り立つことが知られています(この記事では証明しません)。
またこれは今回参考にした文献(1975,1976)が参照している文献(1941)の結果であって、2014年の論文では
$$|N(T)-F(T)|\leq 0.112\log T+0.278\log\log T+2.51+\farc{0.2}T\quad(T\geq e)$$
とあるように$R(T)$の各係数はもっと精密化され続けています。ただ、そこら辺を突き詰めだすとキリがないのでこの記事では元論文に倣って先の不等式を採用するものとします。
証明のあらすじ
まず不等式$|N(T)-F(T)|\leq R(T)$とリーマン予想を使ってチェビシェフ関数$\psi(x)$の素数公式
$$\psi(x)=x-\sum_\rho\farc{x^\rho}\rho-\frac12\log(1-x^{-2})-\log2\pi$$
における振動項$\sum_\rho\farc{x^\rho}\rho$の大きさを推定します。そしてその評価から
$$|\psi(x)-x|<\frac1{8\pi}\sqrt x(\log x-2)\log x\quad(x\geq23\cdot10^8)$$
および
\begin{align}
|\vt(x)-x|&<\frac1{8\pi}\sqrt x(\log x-2)\log x\quad(x\geq23\cdot10^8)\\
|\vt(x)-x|&<\frac1{8\pi}\sqrt x\log^2x\quad(x\geq599)
\end{align}
を示します。あとは$\pi(x)$と$\vt(x)$間の関係式
$$\pi(x)-\Li(x)=\frac{\vt(x)-x}{\log x}+\int^x_2\frac{\vt(t)-t}{t\log^2t}dt+\frac2{\log2}-\Li(2)$$
を使って$x\geq23\cdot10^8$において
$$|\pi(x)-\mathrm{Li}(x)|<\frac1{8\pi}\sqrt x\log x$$
が成り立つことを示し、$2657\leq x<23\cdot10^8$については数値計算で埋め合わせればいい。といった具合になります。
$\psi_1(x)$の素数公式
リーマンゼータ関数を起点とした素数論では$\pi(x),\psi(x)$の素数公式より$\psi_1(x)$の素数公式を考察する方が好まれます。その素数公式というのは
$$\psi_1(x)=\int^x_0\psi(t)dt$$
とおいたとき
$$\psi_1(x)=\frac{x^2}2-\sum_\rho\frac{x^{\rho+1}}{\rho(\rho+1)}-x\log2\pi-\sum^\infty_{n=1}\frac{x^{-2n+1}}{2n(2n-1)}+\farc{\z'(-1)}{\z(-1)}$$
が成り立つ。
というものになっています。どうしてこっちの方が都合がいいのかというとそれは振動項$\sum_\rho\frac{x^{\rho+1}}{\rho(\rho+1)}$が絶対収束することにあります。$\psi(x)$の素数公式では振動項$\sum_\rho\frac{x^\rho}\rho$が条件収束となっているので安易に三角不等式すら使えません。これは振動項の挙動を考察する素数論においては大きなデメリットとなってしまいます。そういうわけで振動項に三角不等式を使ったり積分や極限の順序交換をしたりできる$\psi_1(x)$が重宝されるわけなのです。
素数公式の記事
で示した式
$$\psi(x)=-\frac1{2\pi i}\int^{\s+i\infty}_{\s-i\infty}\frac{\z'(s)}{\z(s)}\frac{x^s}sds$$
を積分することで
$$\psi_1(x)=-\farc1{2\pi i}\int^{\s+i\infty}_{\s-i\infty}\frac{\z'(s)}{\z(s)}\frac{x^{s+1}}{s(s+1)}ds$$
が成り立つ。
また同記事で示した部分分数展開公式
$$-\frac{\z'(s)}{\z(s)}\frac1s=\frac1{s-1}-\frac{\log2\pi}s-\sum_\rho\frac1{\rho(s-\rho)}+\sum^\infty_{n=1}\frac1{2n(s+2n)}$$
を$s+1$で割り、ヘヴィサイドの展開公式を思い出すことで
$$-\frac{\z'(s)}{\z(s)}\frac1{s(s+1)}=\frac1{2(s-1)}-\frac{\log2\pi}s-\sum_\rho\frac1{\rho(\rho+1)(s-\rho)}-\sum^\infty_{n=1}\frac1{2n(2n-1)(s+2n)}+\frac{\z'(-1)}{\z(-1)}\frac1{s+1}$$
がわかるのでこれを
$$\int^\infty_1x^ax^{-s-1}dx=\frac1{s-a}\quad\leftrightarrow\quad\frac1{2\pi i}\int^{\s+i\infty}_{\s-i\infty}\frac{x^s}{s-a}ds=x^a$$
に注意して逆メリン変換することで
$$\psi_1(x)=\frac{x^2}2-\sum_\rho\frac{x^{\rho+1}}{\rho(\rho+1)}-x\log2\pi-\sum^\infty_{n=1}\frac{x^{-2n+1}}{2n(2n-1)}+\farc{\z'(-1)}{\z(-1)}$$
を得る。
ちなみに
\begin{eqnarray}
\sum^\infty_{n=1}\frac{x^{-2n+1}}{2n(2n-1)}
&=&-\sum^\infty_{n=1}\frac{x}{2nx^{2n}}+\sum^\infty_{n=1}\frac1{(2n-1)x^{2n-1}}
\\&=&\frac12x\log(1-x^{-2})+\frac12\log\frac{1+x^{-1}}{1-x^{-1}}
\end{eqnarray}
と表せます。
振動項$\phi(x)$の評価
\begin{align}
\phi(x)&=\psi(x)-x+\frac12\log(1-x^{-2})+\log2\pi\\
&=-\sum_\rho\frac{x^\rho}\rho\\
K_m(x,h)&=\int^h_0\cdots\int^h_0\int^h_0\phi(x+t_1+t_2+\cdots+t_m)dt_1dt_2\cdots dt_m\\
f_{m,n,a}(x,h,t)&=\frac{K_m(x,h)}{h^n}+\frac12nh^a-th^{a-1}
\end{align}
と定める。このとき
\begin{align}
\int^h_0f_{m,n,a}(x,h,t+t_0)dt_0
&=\l(\frac{K_m(x,h)}{h^n}+\frac12nh^a\r)h-\frac12(2th+h^2)h^{a-1}\\\\
&=f_{m,n-1,a+1}(x,h,t)
\end{align}
および$f_{m,0,a}(x,h,0)=K_m(x,h)$より
$$K_m(x,h)=\int^h_0\cdots\int^h_0\int^h_0f_{m,n,a}(x,h,t_1+t_2+\cdots+t_n)dt_1dt_2\cdots dt_n$$
が成り立つことに注意する。
$f_m(x,h,t)=f_{m,m,1}(x,h,t)$とおいたとき
- $h>0$ならば、ある$0\leq t\leq mh$が存在して$\phi(x+t)\leq f_m(x,h,t)$が成り立ち、
- $h<0$ならば、ある$mh\leq t\leq0$が存在して$\phi(x+t)\geq f_m(x,h,t)$が成り立つ。
$h>0$のとき、任意の$0\leq t\leq mh$に対して$\phi(x+t)>f_m(x,h,t)$が成り立つとすると
\begin{eqnarray}
K_m(x,h)&=&\int^h_0\cdots\int^h_0\int^h_0\phi(x+t_1+t_2+\cdots+t_m)dt_1dt_2\cdots dt_m
\\&>&\int^h_0\cdots\int^h_0\int^h_0f_m(x,h,t_1+t_2+\cdots+t_m)dt_1dt_2\cdots dt_m
\\&=&K_m(x,h)
\end{eqnarray}
となって矛盾。
$h<0$のときも同様に、任意の$mh\leq t\leq0$に対して$\phi(x+t)< f_m(x,h,t)$が成り立つとすると
\begin{eqnarray}
(-1)^mK_m(x,h)&=&\int^0_h\cdots\int^0_h\int^0_h\phi(x+t_1+t_2+\cdots+t_m)dt_1dt_2\cdots dt_m
\\&<&\int^0_h\cdots\int^0_h\int^0_hf_m(x,h,t_1+t_2+\cdots+t_m)dt_1dt_2\cdots dt_m
\\&=&(-1)^mK_m(x,h)
\end{eqnarray}
となって矛盾。よって主張を得る。
任意の$0<\d<(x-1)/xm\;(x>1)$に対し
$$\e_{\pm1}=\frac{K_m(x,\pm\d x)}{(\pm x)^{m+1}\d^m}+\frac{m\d}2$$
とおくと
$$-\e_{-1}\leq\frac{\phi(x)}x\leq\e_1$$
が成り立つ。
右側の不等号については$h=\d x$に対して補題2を考えると、ある$0\leq t\leq m\d x$があって
$$\psi(x+t)-(x+t)+\frac12\log(1-(x+t)^{-2})+\log2\pi
\leq\frac{K_m(x,\d x)}{x^m\d^m}+\frac{m\d x}2-t$$
つまり
$$\psi(x+t)-x+\frac12\log(1-(x+t)^{-2})+\log2\pi\leq\e_1x$$
が成り立つ。またそれぞれの単調性から
\begin{align}
\psi(x)&\leq\psi(x+t)\\
\log(1-x^{-2})&\leq\log(1-(x+t)^{-2})
\end{align}
であることに注意すると
$$\psi(x)-x+\frac12\log(1-x^{-2})+\log2\pi=\phi(x)\leq\e_1x$$
を得る。
左側の不等号も同様にある$-m\d x\leq t\leq0$があって
$$\psi(x+t)-x+\frac12\log(1-(x+t)^{-2})+\log2\pi\geq-\e_{-1}x$$
が成り立ち、単調性から
\begin{align}
\psi(x)&\geq\psi(x+t)\\
\log(1-x^{-2})&\geq\log(1-(x+t)^{-2})
\end{align}
なので結局$\phi(x)\geq-\e_{-1}x$を得る。
$K_m(x,\pm\d x)$の評価
$\dis K_m(x,h)=-\sum_\rho\frac1\rho\int^h_0\cdots\int^h_0\int^h_0(x+t_1+t_2+\cdots+t_m)^\rho dt_1dt_2\cdots dt_m$
まず$\psi(x)$と$\psi_1(x)$の素数公式
\begin{align}
\psi&=x-\log2\pi-\sum^\infty_{n=0}\frac{x^{-2n}}{2n}+\phi(x)\\
\int^x_0\psi(x)dx&=\frac{x^2}2-x\log2\pi+\sum^\infty_{n=0}\frac{x^{-2n+1}}{2n(2n+1)}-\sum_\rho\frac{x^{\rho+1}}{\rho(\rho+1)}
\end{align}
を見比べることで
$$\int^h_0\phi(x+t_1)dt_1=-\sum_\rho\frac{(x+h)^\rho-x^\rho}{\rho(\rho+1)}=-\sum_\rho\frac1\rho\int^h_0(x+t_1)^\rho dt_1$$
が成り立つことがわかる。
またこの右辺は絶対収束していたので級数と積分が交換でき、
\begin{eqnarray}
K_m(x,h)&=&\int^h_0\cdots\int^h_0\l(\int^h_0\phi(x+t_1+t_2+\cdots+t_m)dt_1\r)dt_2\cdots dt_m
\\&=&-\sum_\rho\frac1\rho\int^h_0\cdots\int^h_0\int^h_0(x+t_1+t_2+\cdots+t_m)^\rho dt_1dt_2\cdots dt_m
\end{eqnarray}
を得る。
$h=\pm\d x$に対し
$$\l|\int^h_0\cdots\int^h_0\int^h_0(x+t_1+t_2+\cdots+t_m)^\rho dt_1dt_2\cdots dt_m\r|
\leq x^{\b+m}\d^m\frac{2+m\d}{2}$$
が成り立つ。
\begin{eqnarray}
&&\l|\int^h_0\cdots\int^h_0\int^h_0(x+t_1+t_2+\cdots+t_m)^\rho dt_1dt_2\cdots dt_m\r|
\\&\leq&\l|\int^h_0\cdots\int^h_0\int^h_0(x+|t_1|+|t_2|+\cdots+|t_m|)^\b dt_1dt_2\cdots dt_m\r|
\\&=&\int^{|h|}_0\cdots\int^{|h|}_0\int^{|h|}_0(x+t_1+t_2+\cdots+t_m)^\b dt_1dt_2\cdots dt_m
\\&=&\int^\d_0\cdots\int^\d_0\int^\d_0x^\b(1+u_1+u_2+\cdots+u_m)^\b (xdu_1)(xdu_2)\cdots (xdu_m)\quad(t_k=xu_k)
\\&\leq&x^{\b+m}\int^\d_0\cdots\int^\d_0\int^\d_0(1+t_1+t_2+\cdots+t_m)dt_1dt_2\cdots dt_m
\\&=&x^{\b+m}\cdot\d^m\farc{2+m\d}{2}
\end{eqnarray}
のようにしてわかる。(積分の値については漸化式$I_{m+1}=\d I_m+\frac12\d^{m+2}$からわかる。)
$h=\pm\d x$に対して
$$\l|\int^h_0\cdots\int^h_0\int^h_0(x+t_1+t_2+\cdots+t_m)^\rho dt_1dt_2\cdots dt_m\r|
\leq\frac{x^{\b+m}((1+\d)^{m+1}+1)^m}{|\g|^m}$$
が成り立つ。
左辺の積分を計算すると
\begin{eqnarray}
&&\frac1{(\rho+1)(\rho+2)\cdots(\rho+m)}\sum^m_{j=0}(-1)^{m-j}\binom mj(x+jh)^{\rho+m}
\\&=&\frac{x^{\rho+m}}{(\rho+1)(\rho+2)\cdots(\rho+m)}\sum^m_{j=0}(-1)^{m-j}\binom mj(1\pm j\d)^{\rho+m}
\end{eqnarray}
となり、$0<\d<(x-1)/mx<1/m$および$\b<1$より
$$|(1\pm j\d)^{\rho+m}|=(1\pm j\d)^{\b+m}<(1+j\d)^{m+1}<((1+\d)^j)^{m+1}$$
に注意すると
$$\l|\sum^m_{j=0}(-1)^{m-j}\binom mj(1\pm j\d)^{\rho+m}\r|
\leq\sum^m_{j=0}\binom mj((1+\d)^{m+1})^j=((1+\d)^{m+1}+1)^m$$
なのであとは$|z|\geq|\Im(z)|$に注意すればわかる。
リーマン予想が真であるとき、任意の$T>0$に対し
$$\frac1x|\phi(x)|\leq\frac1{\sqrt x}\l(\sum_{0<\g\leq T}\frac{2+m\d}{|\rho|}+2\sum_{\g>T}\frac{((1+\d)^{m+1}+1)^m}{\d^m\g^{m+1}}\r)+\frac{m\d}2$$
が成り立つ。
上で示した種々の結果から
\begin{eqnarray}
\frac1x|\phi(x)|&\leq&\frac{\max_{\pm}|K_m(x,\pm\d x)|}{x^{m+1}\d^m}+\frac{m\d}2
\\&\leq&\farc1{x^{m+1}\d^m}\l(\sum_{|\g|\leq T}x^{\b+m}\d^m\frac{2+m\d}{2|\rho|}+\sum_{|\g|>T}\frac{x^{\b+m}((1+\d)^{m+1}+1)^m}{|\rho|\cdot|\g|^m}\r)+\frac{m\d}2
\\&\leq&\frac1x\l(2\sum_{0<\g\leq T}x^\b\frac{2+m\d}{2|\rho|}+2\sum_{\g>T}x^\b\frac{((1+\d)^{m+1}+1)^m}{\d^m\g^{m+1}}\r)+\frac{m\d}2
\end{eqnarray}
と評価できるので、あとはリーマン予想$\b=\frac12$からわかる。
零点についての和の評価
$(a,b)\;(a>1)$で微分可能な非負値関数$f(t)$が$f'(t)\leq0\quad(\forall t\in(a,b))$を満たすとき
$$\sum_{a<\g\leq b}f(\g)\leq\frac1{2\pi}\int^b_af(t)\log\frac t{2\pi}dt+\l(0.137+\frac{0.433}{\log a}\r)\int^b_a\farc{f(t)}tdt+E(a,b)$$
が成り立つ。ただし
$$E(a,b)=(N(b)-F(b)-R(b))f(b)-(N(a)-F(a)-R(a))f(a)$$
とした。
アーベルの総和公式
と同様にして
$$\sum_{a<\g\leq b}f(\g)=N(b)f(b)-N(a)f(a)-\int^b_aN(t)f'(t)dt$$
が成り立つので
\begin{align}
F'(t)&=\frac1{2\pi}\log\farc t{2\pi}\\
tR'(t)&=0.137+\frac{0.433}{\log t}\\
&\leq0.137+\frac{0.433}{\log a}\quad(a< t)
\end{align}
に注意すると$N(t)< F(t)+R(t)$より
\begin{eqnarray}
\sum_{a<\g\leq b}f(\g)&\leq&N(b)f(b)-N(a)f(a)-\int^b_a(F(t)+R(t))f'(t)dt
\\&=&E(a,b)+\int^b_aF'(t)f(t)dt+\int^b_a\frac{tR'(t)}tf(t)dt
\\&\leq&\frac1{2\pi}\int^b_af(t)\log\frac t{2\pi}dt+\l(0.137+\frac{0.433}{\log a}\r)\int^b_a\farc{f(t)}tdt+E(a,b)
\end{eqnarray}
を得る。
$$T=\frac{(1+\d)^{m+1}+1}\d\l(\frac2{2+m\d}\r)^\frac1m$$
としたとき、$T>D=158.84998$であれば
\begin{align}
&\sum_{0<\g\leq T}\frac{2+m\d}{|\rho|}+2\sum_{\g>T}\frac{((1+\d)^{m+1}+1)^m}{\d^m\g^{m+1}}\\
<{}&\frac{2+m\d}{4\pi}\l(\l(\log\frac T{2\pi}+\frac1m\r)^2+0.038207+\frac1{m^2}-\frac{2.82m}{(m+1)T}\r)
\end{align}
が成り立つ。
$D=158.84998$について、$N(D)=57$および
$$\sum_{0<\g\leq D}\frac1{|\rho|}<0.8113925$$
が知られていることを使う。これは具体的な非自明な零点の(近似)値を求めることでわかるので特に証明はしない。
まず$f(t)=1/t,\ a=D,\ b=T$について補題8を使うことで
\begin{eqnarray}
\sum_{0<\g\leq T}\frac1{|\rho|}
&<&0.8113925+\sum_{D<\g\leq T}\frac1\g
\\&\leq&0.8113925+\frac1{4\pi}\l(\log^2\frac T{2\pi}-\log^2\farc D{2\pi}\r)+\l(0.137+\frac{0.433}{\log D}\r)\l(\farc1D-\frac1T\r)+E
\\&<&\frac1{4\pi}\log^2\frac T{2\pi}+0.0030404-\l(0.137+\frac{0.433}{\log D}\r)\frac1T+(N(T)-F(T)-R(T))\frac1T
\end{eqnarray}
が成り立つ。ただし
$$0.8113925-\frac1{4\pi}\log^2\farc D{2\pi}+\l(F(D)+R(D)-N(D)+0.137+\frac{0.433}{\log D}\r)\farc1D<0.0030404$$
とした。
>>> from numpy import log,pi
>>> d=158.84998
>>> c=d/(2*pi)
>>> N=57
>>> F=c*log(c)-c+7/8
>>> R=0.137*log(d)+0.443*log(log(d))+1.588
>>> 0.8113925-(log(c))**2/(4*pi)+(F+R-N+0.137+0.443/log(d))/d
0.003040395970144244 また
$$\int\frac1{t^{m+1}}\log\frac t{2\pi}dt=\frac{1+m\log(t/2\pi)}{m^2t^m}+C$$
に注意して$f(t)=1/t^{m+1},a=T,b=\infty$について補題7を使うことで
\begin{eqnarray}
\sum_{\g>T}\frac1{\g^{m+1}}
&\leq&\frac1{T^m}\l(\frac1{2\pi m}\log\frac T{2\pi}+\frac1{2\pi m^2}+\l(0.137+\frac{0.433}{\log T}\r)\frac1{(m+1)T}-(N(T)-F(T)-R(T))\frac1T\r)
\\&<&\frac{\d^m(2+m\d)}{2((1+\d)^{m+1}+1)^m}\l(\frac1{4\pi}\l(\frac2m\log\frac T{2\pi}+\frac2{m^2}\r)+\l(0.137+\frac{0.433}{\log D}\r)\frac1{(m+1)T}-(N(T)-F(T)-R(T))\frac1T\r)
\end{eqnarray}
が成り立つので、さっきの不等式と合わせて
\begin{eqnarray}&&
\sum_{0<\g\leq T}\frac{2+m\d}{|\rho|}+2\sum_{\g>T}\frac{((1+\d)^{m+1}+1)^m}{\d^m\g^{m+1}}
\\&<&\frac{2+m\d}{4\pi}\l(\l(\log\frac T{2\pi}+\frac1m\r)^2+4\pi\cdot0.0030404+\frac1{m^2}-\l(0.137+\frac{0.433}{\log D}\r)\l(1-\frac1{m+1}\r)\frac{4\pi}T\r)
\\&<&\frac{2+m\d}{4\pi}\l(\l(\log\frac T{2\pi}+\frac1m\r)^2+0.038207+\frac1{m^2}-\frac{2.82m}{(m+1)T}\r)
\end{eqnarray}
を得る。ただし
$4\pi\cdot0.0030404<0.038207$
$\dis4\pi\l(0.137+\frac{0.433}{\log D}\r)>2.82$
とした。
>>> from numpy import log,pi
>>> 4*pi*0.0030404
0.03820679321589763
>>> 4*pi*(0.137+0.443/log(d))
2.8200430232286395$\psi(x),\vt(x)$の評価
リーマン予想が真であるとき
\begin{align}
|\psi(x)-x|&<\frac1{8\pi}x(\log x-2)\log x\quad(x\geq23\cdot10^8)\\
|\vt(x)-x|&<\frac1{8\pi}x(\log x-2)\log x\quad(x\geq23\cdot10^8)
\end{align}
が成り立つ。
まず任意に$\xi\geq82800$を取って$x\geq\xi$において
$$m=1,\;\d=\frac{\log x}{\pi\sqrt x}$$
として定理7,9を適用する。
このとき
$$\d=\frac1{\log x}\cdot\frac{\log^2x}{\pi\sqrt x}\leq\frac{\a_1}{\log x}\leq\a_2$$
ただし
$$\a_1=\frac{\log^2\xi}{\pi\sqrt\xi},\quad\a_2=\frac{\log\xi}{\pi\sqrt\xi}<0.0126$$
と評価でき、また
\begin{eqnarray}
T&=&\frac{(1+\d)^{m+1}+1}\d\l(\frac2{2+m\d}\r)^\frac1m
=\frac{2(2+2\d+\d^2)}{\d(2+\d)}
=2\l(\frac1\d+1-\frac1{2+\d}\r)
\\&\geq&2\l(\frac1{0.0126}+1-\frac12\r)>158.84998=D
\\\log\frac T{2\pi}+\frac1m&=&\log\frac1{\pi\d}+\log\l(1+\farc{\d(1+\d)}{2+\d}\r)+1
\leq\log\frac{\sqrt x}{\log x}+(\log(1+\d_1)+1)
\\&\leq&\frac12(\log x-2\log\log x+2(1+\d_1))\leq\frac12(\log x-\a_3)
\end{eqnarray}
ただし
$$\d_1=\frac{\a_2(1+\a_2)}{2+\a_2}<0.00634,\quad\a_3=2\log\log\xi-2(1+\d_1)>2.841$$
と評価できることに注意する。
>>> from numpy import log,pi,sqrt
>>> xi=82800
>>> a2=log(xi)/(pi*sqrt(xi))
>>> a2
0.012526849246324731
>>> 2*(1/0.0126+1-1/2)
159.73015873015873
>>> d1=a2*(1+a2)/(2+a2)
>>> d1
0.006302410923419406
>>> a3=2*log(log(xi))-2*(1+d1)
>>> a3
2.841276293240455 いま定理7,9から
\begin{eqnarray}
&&\frac1x|\psi(x)-x|=\frac1x\l|\phi(x)-\frac12\log(1-x^{-2})-\log2\pi\r|
\\&<&\farc{2+\d}{4\pi\sqrt x}\l(\l(\log\frac T{2\pi}+\frac1m\r)^2+0.038207+1-\farc{2.82}{2T}\r)+\frac\d2+\frac1x\l|\farc12\log(1-x^{-2})+\log2\pi\r|
\\&<&\frac1{8\pi\sqrt x}\l(1+\frac{\a_1}{2\log x}\r)((\log x-\a_3)^2+4\cdot1.038207)+\frac{\log x}{2\pi\sqrt x}+\frac1x\log2\pi
\\&\leq&\frac1{8\pi\sqrt x}\l(1+\frac{\a_1}{2\log x}\r)(\log^2x-\a_4\log x)+\frac{\log x}{8\pi\sqrt x}\l(4+\frac{8\pi\log2\pi}{\sqrt x\log x}\r)
\\&\leq&\frac1{8\pi\sqrt x}(\log^2x-\a_5\log x)-\frac1{8\pi\sqrt x}\frac{\a_1\a_4}2
\end{eqnarray}
ただし
$$\a_4=2\a_3-\frac{\a_3^2+4.152828}{\log\xi},\quad\a_5=a_4-\frac{\a_1}2-4-\frac{8\pi\log2\pi}{\sqrt\xi\log\xi}$$
と評価できる。
ここで$2x-x^2/a$は$0\leq x\leq a$で単調増加であり、また$\a_3<2\log\log\xi<\log\xi$であることに注意すると
$$\a_4>2\cdot2.841-\frac{2.841^2+4.152828}{\log\xi}>0$$
となるので、結局
$$|\psi(x)-x|<\farc1{8\pi}\sqrt x(\log x-\a_5)\log x$$
と評価できることになる。
>>> from numpy import log
>>> xi=82800
>>> 2*2.841-(2.841**2+4.152828)/log(xi)
4.602530634962593 そして
$$0\leq\psi(x)-\vt(x)<\vt(\sqrt x)+3x^\frac13\quad(x>0)$$
および
$$\vt(x)<1.02x\quad(x>0)$$
が成り立つことが知られているので
$$|\vt(x)-x|<|\psi(x)-x|+1.02\sqrt x+3x^\frac13<\frac1{8\pi}\sqrt x(\log x-\a_6)\log x$$
ただし
$$\a_6=\a_5-\farc{8.16\pi}{\log\xi}-\farc{24\pi}{\xi^\frac16\log\xi}$$
と評価でき、$\xi\geq82800$は任意であったので$\xi=23\cdot10^8$とおくことで$\a_5>\a_6>2$となり主張を得る。
>>> from numpy import sqrt,power,log,pi
>>> xi=23*10**8
>>> a2=log(xi)/(pi*sqrt(xi))
>>> d1=a2*(1+a2)/(2+a2)
>>> a3=2*log(log(xi))-2*(1+d1)
>>> a4=2*a3-(a3**2+4.152828)/log(xi)
>>> a5=a4-a2*log(xi)/2-4-8*pi*log(2*pi)/(sqrt(xi)*log(xi))
>>> a6=a5-8.16*pi/log(xi)-24*pi/(power(xi,1/6)*log(xi))
>>> a6
2.00704868502812 リーマン予想が真であるとき
\begin{align}
|\psi(x)-x|&<\frac1{8\pi}\sqrt x\log^2x\quad(x\geq73.2)\\
|\vt(x)-x|&<\frac1{8\pi}\sqrt x\log^2x\quad(x\geq599)
\end{align}
が成り立つ。
定理9と同様に評価し、$\xi=e^{16}<10^7$とおくことで$\a_5>\a_6>0$がわかるので$x\geq e^{16}$においては所望の不等式が成り立つ。
>>> from numpy import sqrt,power,log,pi,e
>>> xi=e**16
>>> a2=log(xi)/(pi*sqrt(xi))
>>> d1=a2*(1+a2)/(2+a2)
>>> a3=2*log(log(xi))-2*(1+d1)
>>> a4=2*a3-(a3**2+4.152828)/log(xi)
>>> a5=a4-a2*log(xi)/2-4-8*pi*log(2*pi)/(sqrt(xi)*log(xi))
>>> a6=a5-8.16*pi/log(xi)-24*pi/(power(xi,1/6)*log(xi))
>>> a6
0.09834137524507225 $x< e^{16}$においては数値計算で示すのも現実的だが、元論文に倣ってもう少し不等式評価しておく。
いま$0< x\leq10^8$において
$$0< x-\vt(x)<2.05282\sqrt x$$
が成り立つことが知られているので$1400\leq x< e^{16}$においては
$$|\vt(x)-x|<\frac{2.05282}{\log^21400}\sqrt x\log^2x<\frac1{8\pi}\sqrt x\log^2x$$
と評価できる。
また
$$0\leq\psi(x)-\vt(x)<\vt(\sqrt x)+3x^\frac13\quad(x>0)$$
が知られていたことを思い出すと$1400\leq x< e^{16}$において
\begin{align}
\psi(x)-x&\geq\vt(x)-x\\
&>-\frac1{8\pi}\sqrt x\log^2x\\
\psi(x)-x&<\psi(x)-\vt(x)<\sqrt x+3x^\frac13\\
&\leq\frac1{\log^21075}\l(1+\frac3{1075^\frac16}\r)\sqrt x\log^2x\\
&<\frac1{8\pi}\sqrt x\log^2x
\end{align}
と評価できる。
>>> from numpy import log,pi
>>> 2.05282/(log(1400)**2)
0.03911710512821552
>>> (1+3/power(1075,1/6))/log(1075)**2
0.039763115286937885
>>> 1/(8*pi)
0.039788735772973836 $x<1400$については数値計算で示せばよい。実際に$x-\psi(x)$を緑、$x-\vt(x)$を橙、$\pm\sqrt x\log^2x/8\pi$を黄色としてグラフで見てみると次のようになっている。
 x≤1500での様子
x≤1500での様子
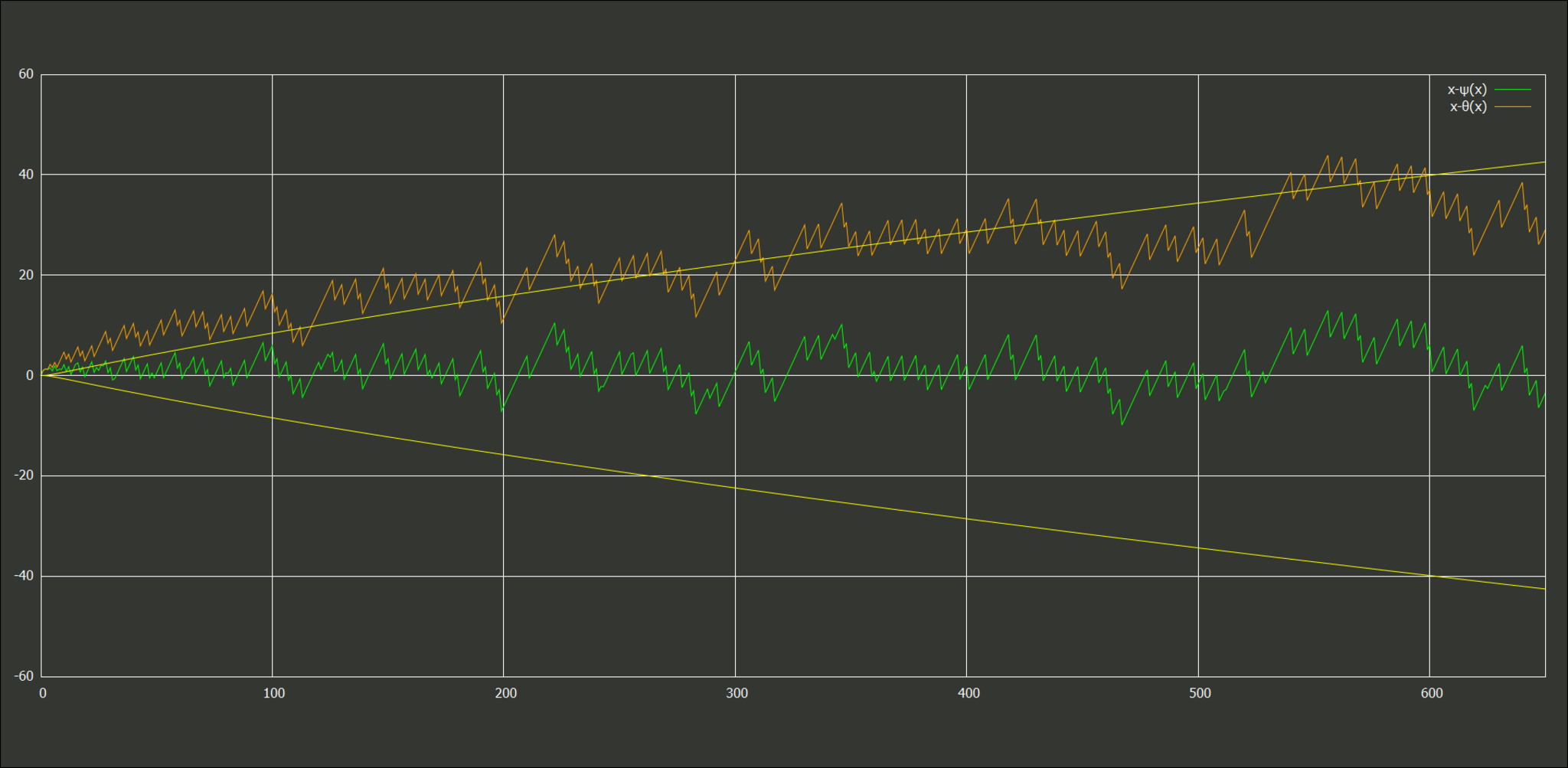 x≤650での様子
x≤650での様子
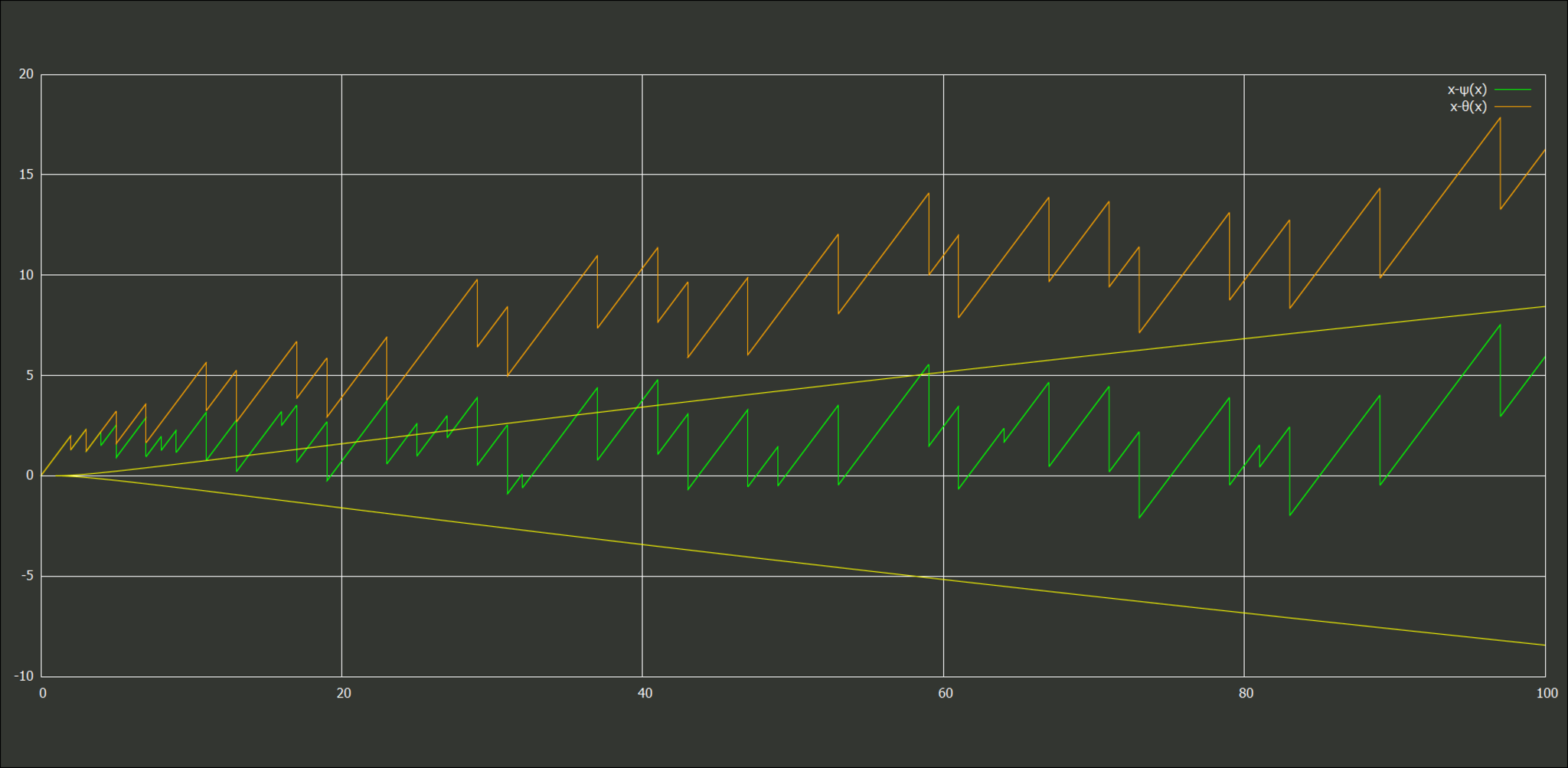 x≤100での様子
x≤100での様子
(これを見る限り$|\psi(x)-x|<\sqrt x\log^2x/8\pi$は$x\geq59$で成り立っていそうだが...?)
$\pi(x)$の評価
リーマン予想が真であるとき
$$|\pi(x)-\Li(x)|<\frac1{8\pi}\sqrt x\log x\quad(x\geq2657)$$
が成り立つ。
この記事
で示したように
$$\pi(x)-\Li(x)=\frac{\vt(x)-x}{\log x}+\int^x_2\frac{\vt(t)-t}{t\log^2t}dt+\frac2{\log2}-\Li(2)$$
が成り立つので、$\xi\geq599$において
$$\xi'=\frac{\vt(\xi)-\xi}{\log\xi}-(\pi(\xi)-\Li(\xi))=-\int^\xi_2\frac{\vt(t)-t}{t\log^2t}dt-\l(\frac2{\log2}-\Li(2)\r)$$
とおくと$x\geq23\cdot10^8$において
\begin{eqnarray}
|\pi(x)-\Li(x)|&<&\l|\frac{\vt(x)-x}{\log x}+\int^x_\xi\frac{\vt(t)-t}{t\log^2t}dt-\xi'\r|
\\&\leq&\frac1{8\pi}\sqrt x(\log x-2)+\frac1{8\pi}\int^x_\xi\frac{dt}{\sqrt t}+|\xi'|
\\&=&\frac1{8\pi}\sqrt x\log x+|\xi'|-\frac{\sqrt\xi}{4\pi}
\end{eqnarray}
と評価できる。いま$\xi=10^8$とおくと$\xi'\sim89.71<7853.98\sim\sqrt\xi/4\pi$となるので所望の不等式が成り立つ。
$x<23\cdot10^8$においては数値計算で示すのも現実的ではあるが、元論文に倣ってもう少し不等式評価しておく。(本来$\li(x)$のところを$\Li(x)=\li(x)+1.04516\ldots$に置き換えているのでところどころ主張を書き換えてある。)
まず$p\leq50\cdot10^8$なる任意の素数$p$について$\Li(p)-\pi(p)\leq4613$が成り立つことが知られているので$5\cdot10^7\leq x\leq49\cdot10^8$において$x$より大きい素数の中で最小のものを$p$とおくと
$$|\pi(x)-\Li(x)|=\Li(p)-(\pi(p)-1)\leq4614<\frac1{8\pi}\sqrt x\log x$$
と評価できる。(現時点で$\Li(x)-\pi(x)<0$となるような$x$は知られていないことに注意する。)
>>> from numpy import sqrt,log,pi
>>> sqrt(x)*log(x)/(8*pi)
4987.621160107788 $4000\leq x\leq 5\cdot10^7$においては
$$0<\Li(x)-\pi(x)<2.661\frac{\sqrt x}{\log x}$$
が成り立つことが知られている(結局数値計算?)ことから
$$\Li(x)-\pi(x)<\frac{2.661}{\log^2(4000)}\sqrt x\log x<\frac1{8\pi}\sqrt x\log x$$
を得る。あとは数値計算で示せばよい。
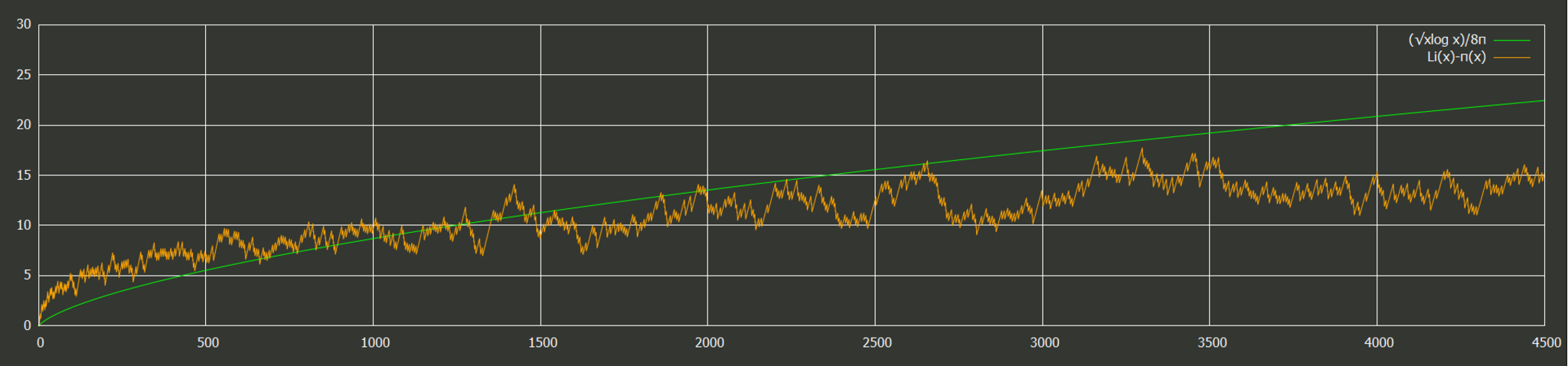 x≤4500での様子
x≤4500での様子
ちなみに$\li(x)-\pi(x)$をグラフにすると次のようになる。
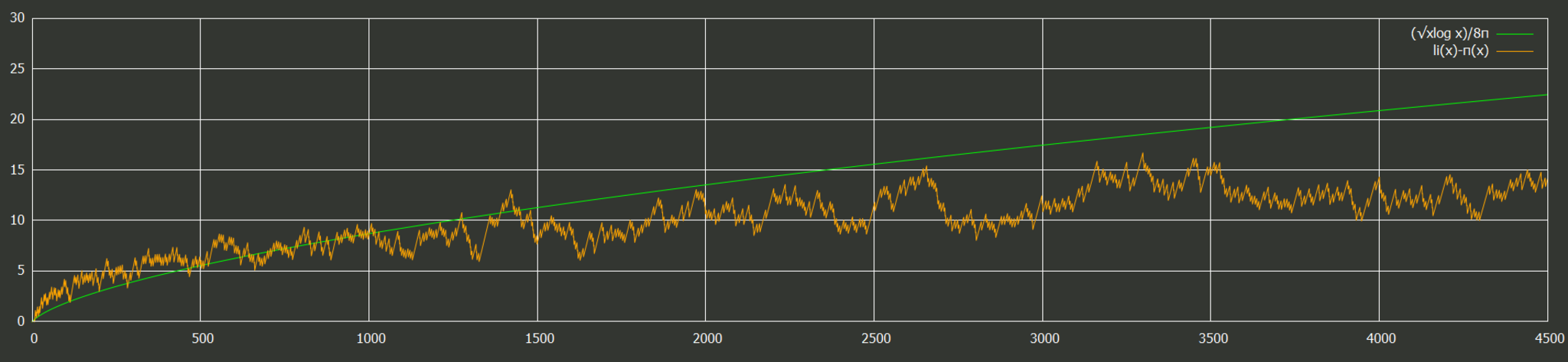 x≤4500での様子
x≤4500での様子
これを見る限り$|\pi(x)-\li(x)|<\sqrt x\log x/8\pi$は$x\geq1447$で成り立ちそうであるが、元論文ではあくまで$x\geq2657$となっている。
おわりに
とりあえず目的の不等式を示すことはできましたが、途中で証明なしに
$$\l|N(T)-\frac T{2\pi}\log\frac T{2\pi}-\frac T{2\pi}+\frac78\r|\leq0.137\log T+0.443\log\log T+1.588\quad(T>2)$$
であることと
$$0\leq\psi(x)-\vt(x)<\vt(\sqrt x)+3x^\frac13\quad(x>0)$$
および
$$\vt(x)<1.02x\quad(x>0)$$
が成り立つことを使いました。これらについてはいつか記事を書くかもしれませんし書かないかもしれません。詳しく知りたい人は
こちら
とか
そちら
を参照してください。
ちなみにこれら以外に未証明で使った不等式は単純な数値計算で省略できますが、この証明が書かれた年代(1976)を考えるとまだ計算機器が充実していない(と思われる)以上そういうわけにはいかなかったのだと思います。個人のパソコンでもこの程度の計算はできる(多分)ことに感謝するのと同時に、パソコンの無い時代にこれだけの結果に辿り着いた先人たちの逞しさに感服する限りですね。
