積分問題集の解説(超級)

今記事では
$β_n:=\binom{2n}{n}2^{-2n}$
とします.

特殊関数を含む積分は級数展開が使える場合があります.
\begin{eqnarray} K(x):&=&\int_{0}^{1}\frac{dt}{\sqrt{1-t^2}\sqrt{1-x^2t^2}}\\ &=&\sum_{n≥0}β_n x^{2n}\int_{0}^{1}\frac{t^{2n}}{\sqrt{1-t^2}}dt\\ &=&\frac{π}{2}\sum_{n≥0}β_n^2x^{2n} \end{eqnarray}
と級数展開できます.
ではこれを今回の問題に使ってみましょう.
\begin{eqnarray} \int_{0}^{1}\frac{K(tx)}{\sqrt{1-x^2}}dx&=& \frac{π}{2}\sum_{n≥0}β_n^2t^{2n}\int_{0}^{1}\frac{t^{2n}}{\sqrt{1-t^2}}dt\\ &=&\frac{π^2}{4}\sum_{n≥0}β_n^3t^{2n} \end{eqnarray}
つまり
\begin{eqnarray} \sum_{n≥0}β_n^3t^{2n}=\left(\sum_{n≥0}β_n^2\left(\frac{1-\sqrt{1-t^2}}{2}\right)^n\right)^2 \end{eqnarray}
を示すことになります.
見通しの良いように超幾何級数にしてみましょう
\begin{eqnarray} F\left[\begin{array}11/2,1/2,1/2\\1,1\end{array};t^2\right]=F\left[\begin{array}11/2,1/2\\1\end{array};\frac{1-\sqrt{1-t^2}}{2}\right]^2 \end{eqnarray}
あとは左辺を変形して成り立つことを確かめましょう.

1つ目の公式をclausenの公式といいます.これは3F2の級数を2F1にできる素晴らしい公式ですね.
では変形させていきましょう.
\begin{eqnarray} F\left[\begin{array}11/2,1/2,1/2\\ 1,1\end{array};t^2\right]&=&F\left[\begin{array}11/4,1/4\\1\end{array};t^2\right]^2\\ &=&F\left[\begin{array}11/2,1/2\\1\end{array};\frac{1-\sqrt{1-t^2}}{2}\right]^2\\ &=&\frac{4}{π^2}K^2\left(\sqrt{\frac{1-\sqrt{1-t^2}}{2}}\right) \end{eqnarray}
これにより題意が示されました.
またt=1のときはDixonの恒等式でも計算できます.

これらは同じ解法があるので一緒に解説してしまいます.
先ず次がわかります.
\begin{eqnarray} \Re\frac{1}{\ln(t\cos x)-ix}=\frac{\ln(t\cos x)}{\ln^2(t\cos x)+x^2} \end{eqnarray}
\begin{eqnarray} \Im\frac{1}{\ln(t\sin x)-ix}=\frac{x}{\ln^2(t\sin x)+x^2} \end{eqnarray}
ここで今まで通り
\begin{eqnarray} \frac{1}{f^s}=\frac{1}{Γ(s)}\int_{0}^{∞}u^{s-1}e^{-ft}dt \end{eqnarray}
を用います.
$\ln t\cos x,\ln t\sin x<0$であるため
$-\ln t\cos x+ix,-\ln t\sin x+ix$を分母に
しなければいけません.
それに注意して解いていきましょう.
\begin{eqnarray} \Re\int_{0}^{π/2}\frac{dx}{(-\ln(t\cos x)+ix)^s}&=&\frac{1}{Γ(s)}\int_{0}^{π/2}\int_{0}^{∞}u^{s-1}t^u \cos^ux\cos uxdudx\\ &=&\frac{π}{2Γ(s)}\int_{0}^{∞}u^{s-1}e^{-u\ln\frac{2}{t}}du\\ &=&\frac{π}{2\ln^s\frac{2}{t}} \end{eqnarray}
\begin{eqnarray} \int_{0}^{π}\frac{dx}{(-\ln(t\sin x)+ix)^s}&=&\frac{1}{Γ(s)}\int_{0}^{π} \int_{0}^{∞}u^{s-1}\sin^ux e^{-iux}dudx\\ &=&\frac{π}{Γ(s)}\int_{0}^{∞}u^{s-1}e^{-u(\ln\frac{2}{t}+iπ/2)}du\\ &=&\frac{π}{(\ln\frac{2}{t}+\frac{πi}{2})^s} \end{eqnarray}
あとはs→1とすることにより題意を得られます.
途中の変形で実数乗を含む三角関数の積分がありましたがこれは更に一般的な物をまめけびさんが証明しています.

ベータ関数の逆数の積分表示

また,湧水さんの昔の記事で対数verの積分を証明されています.

積分解説6

これをtについて微分することによりcosの方を示すことができます.

題意は
\begin{eqnarray} f(x)=\frac{\tan^{-1}\frac{1}{1+x^2}}{\sqrt{1+x^2}} \end{eqnarray}
において
\begin{eqnarray} \int_{0}^{1}\frac{1}{x^2}(f(0)-f(x))dx \end{eqnarray}
となっています.
ここで次の積分を用います.
\begin{eqnarray} \int_{0}^{1}\frac{dt}{t^2+a^2}=\frac{\tan^{-1}\frac{1}{a}}{a} \end{eqnarray}
これにより次のように変形できます.
\begin{eqnarray} \int_{0}^{1}\frac{π}{4x^2}-\frac{\tan^{-1}\frac{1}{\sqrt{x^2+1}}}{x^2\sqrt{x^2+1}}dx&=&\int_{0}^{1}\frac{1}{x^2}\int_{0}^{1}\frac{1}{1+y^2}-\frac{1}{1+x^2+y^2}dydx\\ &=&\int_{0}^{1}\int_{0}^{1}\frac{dxdy}{(1+y^2)(1+x^2+y^2)} \end{eqnarray}
penta さんが解法をくださったのでそれを紹介します.

素晴らしい解法ですね！
また,別の解き方では次のような物があります.

こんな感じで重積分でも解くことができます.

途中の計算で
$\frac{\cos nx}{n^2+y^2}$
が出るように積分を調整することにより次を得ます.

これはかなり難しい積分だと思います！
今回は複素積分を用いていきます.
まず被積分関数ですが次のように部分分数分解できます.
\begin{eqnarray} \frac{1+s\cosh πx}{1+2s\cosh πx+s^2}=\frac{1}{2}(\frac{1}{1+se^{πx}}+\frac{1}{1+se^{-πx}}) \end{eqnarray}
これを用いて変形していきましょう.
\begin{eqnarray} \frac{1}{2}\int_{-∞}^{∞}(\frac{1}{1+se^{πx}}+\frac{1}{1+se^{-πx}})\frac{dx}{1+x^2}&=&\int_{-∞}^{∞} \frac{1}{1+se^{-πx}}\frac{dx}{1+x^2}\\ &=&π\int_{0}^{\infty}\frac{dx}{x+s}\frac{1}{\ln^2x+π^2}\\ &=&\frac{1}{2i}\int_{0}^{\infty} \frac{dx}{x+s}(\frac{1}{\ln x-iπ}-\frac{1}{\ln x+iπ}) \end{eqnarray}
ここで
\begin{eqnarray} f(z):=\frac{1}{z+s}\frac{1}{\ln z-iπ} \end{eqnarray}
とし,$f(e^{2πi}z)$において分母が
$\ln z+iπ$となる性質を利用します.
積分経路は次の経路です(手書き)

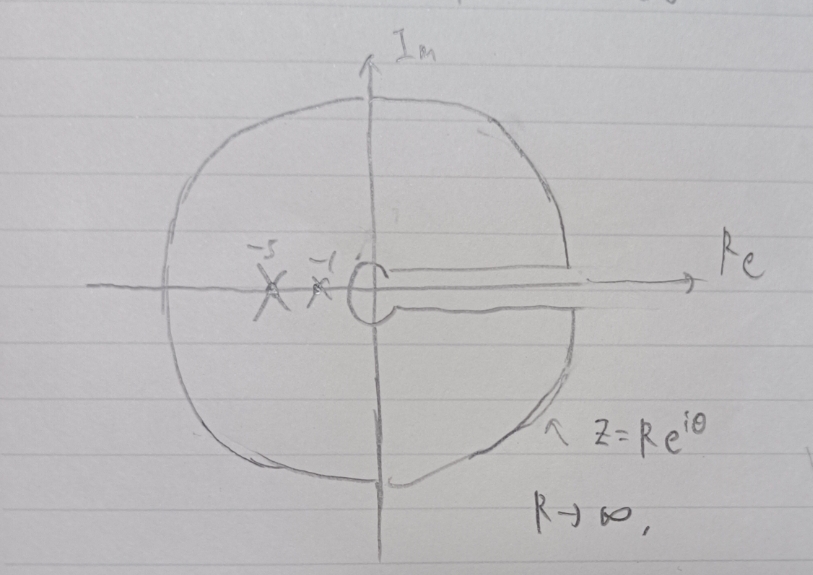
\begin{eqnarray} \oint f dz&=&2πi(\mathrm{Res}_{z=-1}+\mathrm{Res}_{z=-s})f(z)\\ &=&2πi(\frac{1}{1-s}+\frac{1}{\ln s}) \end{eqnarray}
\begin{eqnarray} \oint f dz&=&\int_{0}^{2π} f Rie^{iθ}dθ+\int_{0}^{R} f(x)+f(e^{2πi}x)dx \end{eqnarray}
\begin{eqnarray} \rightarrow^{R→∞}\int_{0}^{∞}\frac{dx}{x+s}(\frac{1}{\ln x-iπ}-\frac{1}{\ln x+iπ}) \end{eqnarray}
\begin{eqnarray} \therefore \int_{-∞}^{∞}\frac{1+s\cosh πx}{1+2s\cosh πx+s^2}\frac{dx}{1+x^2}=π(\frac{1}{1-s}+\frac{1}{\ln s}) \end{eqnarray}
こんな感じでした！
被積分関数や積分経路が難しいですが解けた人がいたのでよかったです.

良い形になるまで変形していきます.
$1+x^2$から$x→\tan x$が直感的に良さそうと思う気がします.
この直感に従って変形していきましょう.
\begin{eqnarray} \int_{0}^{∞}\arctan^2\frac{2ax}{1-a+(1+a)x^2}\frac{dx}{1+x^2}&=& \int_{0}^{π/2}\arctan^2\frac{2a\sin x\cos x}{(1-a)\cos^2x+(1+a)\sin^2x}dx\\ &=&\int_{0}^{π/2}\arctan^2\frac{a\sin 2x}{1-a\cos 2x}dx\\ &=&\sum_{n,m>0}\frac{a^{n+m}}{2nm}\int_{0}^{π}\sin nx\sin mxdx\\ &=&\frac{π}{4}\sum_{n=m>0}\frac{a^{n+m}}{nm}\\ &=&\frac{π}{4}\mathrm{Li}_2(a^2) \end{eqnarray}
中級で紹介したフーリエ級数展開を用いました.(証明はaで微分し級数展開して積分することで示せます.)
そして三角関数の直交性も用いました.

留数定理を用います.
多分アベルプラナの和公式と呼ばれるようなものです.
s/2位とか意味わからん事は考えずそこが領域内に入らないように経路を取りたいです.
そしてもう1つ注意したいのが$e^{2πx}-1$です.
これは単純な経路だと発散してしまう場合があるので適切な経路を用意してあげましょう.
\begin{eqnarray} f(z):=\frac{1}{(a-iz)^s}\frac{1}{e^{2πz}-1} \end{eqnarray}
この虚部を取ってあげれば題意と一致します.
$x=-ia$が中に入らないようにします.(手書き)

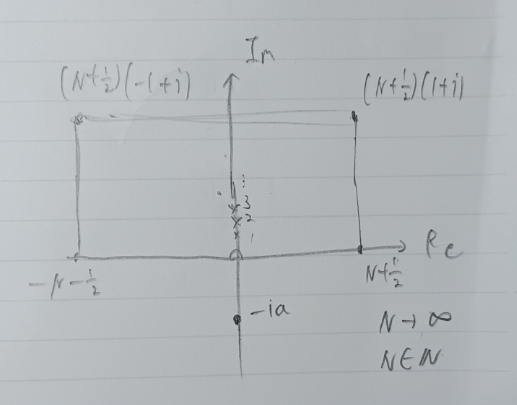
何故N+1/2なのかというとNだと$e^{2πz}-1$により発散してしまうからです.
ではこの経路に沿って積分してあげましょう.
\begin{eqnarray} \oint f dz →\int_{-∞}^{∞}\frac{1}{(a-ix)^s}\frac{dx}{e^{2πx}-1} \end{eqnarray}
\begin{eqnarray} \oint f dz&=&2πi(\frac{1}{2}\mathrm{Res}_{z=0}+\sum_{n=1}^{N}\mathrm{Res}_{z=ni})f\\ &=&i(\frac{1}{2a^s}+\sum_{n=1}^{N}\frac{1}{(a+n)^s})\\ \end{eqnarray}
2つの式について虚部を取ることに
より題意が示せました.
ちなみにアベルプラナの和公式はこちらです↓

wikipedia

今回は3つの解き方を紹介します.
どれも奥深すぎるので調べる際は1つ1つ調べると良いかもしれません.

1 反復ベータ積分

反復ベータ積分の応用:楕円積分のモーメントを計算する

この黒ｲﾄさんの記事で紹介されているモーメントを用いることにより反復ベータ積分に帰着させます.
\begin{eqnarray} \int_{0}^{1}xK^2(x)dx&=&\frac{π}{2}\sum_{n≥0}β_n^2\int_{0}^{1}x^{2n+1}K(x)dx\\ &=&\frac{π}{2}\sum_{n≥0}\frac{β_n^2}{4(n+1)^2β_{n+1}^2}\sum_{n≥m≥0}β_m^2\\ &=&\frac{π}{2}\sum_{n≥m≥0}\frac{β_m^2}{(2n+1)^2}\\ \end{eqnarray}
\begin{eqnarray} \sum_{m≥0}β_m\int_{0}^{x}\frac{t^{2n}}{\sqrt{1-t^2}}dt=\sum_{n≥m≥0}\frac{β_m^2}{(2n+1)β_n}x^{2n+1}\sqrt{1-x^2} \end{eqnarray}
\begin{eqnarray} \int_{0}^{x}\frac{ds}{s\sqrt{1-s^2}}\int_{0}^{s}\frac{dt}{1-t^2}=\sum_{n≥m≥0}\frac{β_m^2}{(2n+1)^2β_n}x^{2n+1} \end{eqnarray}
\begin{eqnarray} \int_{0}^{1}\frac{1}{x\sqrt{1-x^2}}\int_{0}^{x}\frac{1}{s\sqrt{1-s^2}}\int_{0}^{t}\frac{dt}{1-t^2} =\frac{π}{2}\sum_{n≥m≥0}\frac{β_m^2}{(2n+1)^2} \end{eqnarray}
区間通り積分していけば
\begin{eqnarray} \int_{0}^{1}\ln\frac{1+\sqrt{1-s^2}}{1-\sqrt{1-s^2}}\ln\frac{1+s}{1-s}\frac{ds}{4s\sqrt{1-s^2}} \end{eqnarray}
となりますが,
前回紹介した
$x=\frac{2v}{1+v^2}$の置換により
\begin{eqnarray} \int_{0}^{1}\frac{dv}{v}\int_{0}^{v}\frac{du}{u}\int_{0}^{u}\frac{2}{1-t^2}dt=\sum_{n≥0}\frac{2}{(2n+1)^3}=\frac{7}{4}ζ(3) \end{eqnarray}
と計算できます.

2 直交多項式

$P_n$を ルジャンドル多項式 とします.
次の性質があります.
\begin{eqnarray} \frac{1}{\sqrt{1-2xt+t^2}}=\sum_{n≥0}P_n(x)t^n \end{eqnarray}
\begin{eqnarray} \int_{-1}^{1}P_n(x)P_m(x)dx&=&\frac{δ_{mn}}{n+\frac{1}{2}}\\ \int_{0}^{1}P_n(2x-1)P_m(2x-1)dx&=&\frac{δ_{mn}}{2n+1} \end{eqnarray}
これは直交性ですね.
そして楕円積分はルジャンドル多項式を用いて次のように級数で表せます.
\begin{eqnarray} K(\sqrt{x})=\sum_{n≥0}\frac{P_n(2x-1)}{n+\frac{1}{2}} \end{eqnarray}
ではこれらを用いて解いてみましょう.
\begin{eqnarray} \int_{0}^{1}xK^2(x)dx&=&\frac{1}{2}\int_{0}^{1}K^2(\sqrt{x})dx\\ &=&\sum_{n,m≥0}\frac{2}{(2n+1)(2m+1)}\int_{0}^{1}P_n(2x-1)P_m(2x-1)dx\\ &=&\sum_{n≥0}\frac{2}{(2n+1)^3}\\ &=&\frac{7}{4}ζ(3) \end{eqnarray}
直交多項式はもっともっと凄い事ができるので調べてみてほしいです.

3 置換

テータ関数と楕円積分の関係を用います.

便利さんの次の記事を参考にしていきます.

https://mathlog.info/articles/3151

定理6から
\begin{eqnarray} \theta_3(e^{-πK'/K})=\sqrt{\frac{2K}{π}} \end{eqnarray}
ですね.
2,4についても楕円積分で表現していきたいです.
次の事が変形していくことでわかります.
\begin{eqnarray} \theta_3^2(q)=\theta_2^2(q^2)+\theta_3^2(q^2) \end{eqnarray}
そして定理8から次がわかります.
\begin{eqnarray} \frac{1}{2}\frac{K'}{K}=\frac{K'(l)}{K(l)},l=\frac{2\sqrt{k}}{1+k} \end{eqnarray}
これらを用いて2を楕円積分で表します.
\begin{eqnarray} \theta_2^2(e^{-πK'/K})&=&\theta_3^2(e^{-πK'/2K})-\theta_3^2(e^{-πK'/K})\\ &=&\frac{2}{π}(K(l)-K)\\ &=&\frac{2kK}{π} \end{eqnarray}
途中,$K(l)=(1+k)K$を用いました.
そして定理3より
\begin{eqnarray} \theta_4(e^{-πK'/K})=\sqrt{\frac{2k'K}{π}} \end{eqnarray}
も求まります.
今回導出した物らを用いて
\begin{eqnarray} \int_{0}^{∞}t^{s-1}f(\theta_2^2(e^{-t}),\theta_3^2(e^{-t}),\theta_4^2(e^{-t}))dt&=&-\int_{0}^{1}\left(π\frac{K'}{K}\right)^{s-1} f\left(\frac{2kK}{π},\frac{2K}{π},\frac{2k'K}{π}\right)dk\left(\frac{d}{dk}π\frac{K'}{K}\right)\\ &=&\frac{π^{s+1}}{2}\int_{0}^{1}\frac{1}{kk'^2K^2}\left(\frac{K'}{K}\right)^{s-1}f\left(\frac{2kK}{π},\frac{2K}{π},\frac{2k'K}{π}\right)dk \end{eqnarray}
となります.
では今回の題意を計算して見ましょう.
\begin{eqnarray} \int_{0}^{1}kK^2dk&=&2π^{3-s}\int_{0}^{∞}t^{s-1}\theta_2^4(e^{-t})\theta_4^4(e^{-t})dt_{s=1}\\ &=&2π^{3-s}\int_{0}^{∞}\sum_{n≥1}(-1)^n\frac{n^3e^{-nt}}{1-e^{-2nt}}dt\\ &=&2π^{3-s}Γ(s)η(s-3)λ(s)\\ &=&\frac{7}{4}ζ(3) \end{eqnarray}
途中, 子葉さんの記事 にある
$\theta_2^4\theta_4^4$の式を用いました.
また、見当もつかない物が全然あります.

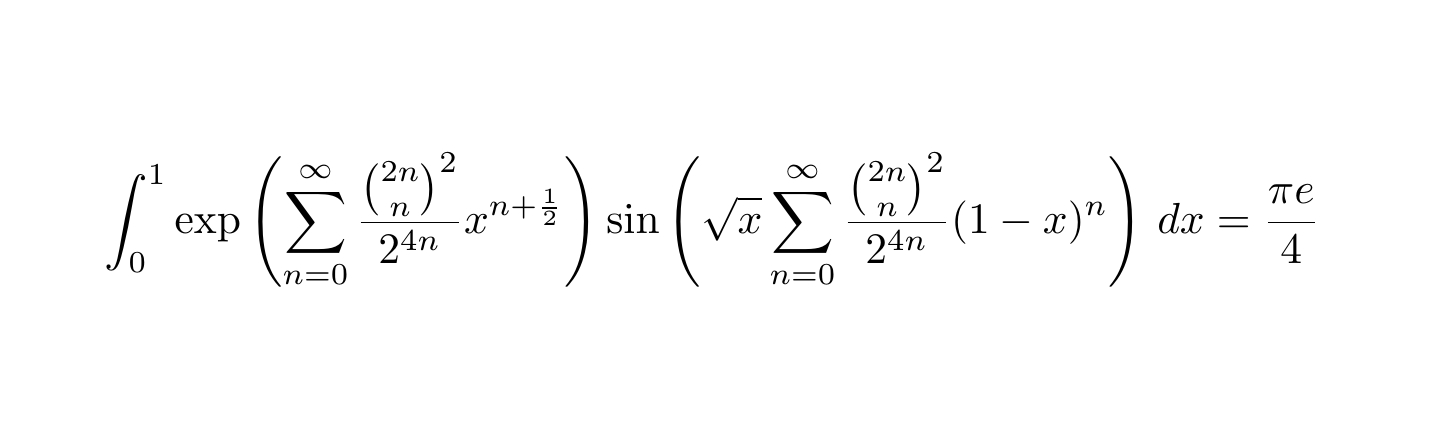
元ツイ
あとは分母に$K'^2+K^2$のある積分達です.

K²+K'²を分母にもつ関数の定積分

感覚的には何か良い直交多項式表示があるのかな？という感じですがまだ直交多項式について全く勉強できていないので全然わかりません.

参考文献

https://t.co/NjSAxybZbK