文献あり

【超局所層理論第7回】Stratifiedモース理論と超局所層理論，近接・消滅サイクル

458

$$\newcommand{bbC}[0]{\mathbb C} \newcommand{bbN}[0]{\mathbb N} \newcommand{bbR}[0]{\mathbb R} \newcommand{bbZ}[0]{\mathbb Z} \newcommand{bfk}[0]{\mathbb{k}} \newcommand{C}[0]{\mathsf{C}} \newcommand{cA}[0]{\mathcal{A}} \newcommand{cB}[0]{\mathcal{B}} \newcommand{Cb}[0]{\mathsf{C}^\mathrm{b}} \newcommand{cC}[0]{\mathcal{C}} \newcommand{cD}[0]{\mathcal{D}} \newcommand{cHom}[0]{\mathcal{H}om} \newcommand{cI}[0]{\mathcal{I}} \newcommand{cJ}[0]{\mathcal{J}} \newcommand{cM}[0]{\mathcal{M}} \newcommand{Cm}[0]{\mathsf{C}^-} \newcommand{cO}[0]{\mathcal O} \newcommand{Coker}[0]{\operatorname{Coker}} \newcommand{Cp}[0]{\mathsf{C}^+} \newcommand{cRHom}[0]{R\mathcal{H}om} \newcommand{cT}[0]{\mathcal{T}} \newcommand{D}[0]{\mathsf{D}} \newcommand{Db}[0]{\mathsf{D}^\mathrm{b}} \newcommand{DbCc}[0]{\mathsf{D}^\mathrm{b}_{\text{$\mathbb{C}$-c}}} \newcommand{DbRc}[0]{\mathsf{D}^\mathrm{b}_{\text{$\mathbb{R}$-c}}} \newcommand{DbwCc}[0]{\mathsf{D}^\mathrm{b}_{\text{w-$\mathbb{C}$-c}}} \newcommand{DbwRc}[0]{\mathsf{D}^\mathrm{b}_{\text{w-$\mathbb{R}$-c}}} \newcommand{dim}[0]{\operatorname{dim}} \newcommand{Dm}[0]{\mathsf{D}^-} \newcommand{Dp}[0]{\mathsf{D}^+} \newcommand{End}[0]{\operatorname{End}} \newcommand{Ext}[0]{\operatorname{Ext}} \newcommand{Hom}[0]{\operatorname{Hom}} \newcommand{id}[0]{\mathrm{id}} \newcommand{Image}[0]{\operatorname{Im}} \newcommand{Int}[0]{\mathrm{Int}} \newcommand{K}[0]{\mathsf{K}} \newcommand{Kb}[0]{\mathsf{K}^\mathrm{b}} \newcommand{Ker}[0]{\operatorname{Ker}} \newcommand{Km}[0]{\mathsf{K}^-} \newcommand{Kp}[0]{\mathsf{K}^+} \newcommand{lten}[0]{\overset{L}{\otimes}} \newcommand{lto}[0]{\longrightarrow} \newcommand{Mc}[0]{\mathrm{Mc}} \newcommand{Mod}[0]{\operatorname{Mod}} \newcommand{MS}[0]{\operatorname{SS}} \newcommand{MS}[0]{\mathrm{SS}} \newcommand{op}[0]{\mathrm{op}} \newcommand{or}[0]{\mathrm{or}} \newcommand{plushat}[0]{\widehat{+}} \newcommand{PSh}[0]{\mathrm{PSh}} \newcommand{pt}[0]{\mathrm{pt}} \newcommand{RG}[0]{R\Gamma} \newcommand{RHom}[0]{R\mathrm{Hom}} \newcommand{Sh}[0]{\mathrm{Sh}} \newcommand{simto}[0]{\overset{\sim}{\to}} \newcommand{supp}[0]{\operatorname{supp}} \newcommand{Supp}[0]{\operatorname{Supp}} \newcommand{tl}[0]{\widetilde} \newcommand{toone}[0]{\overset{+1}{\to}} $$

はじめに

こんにちは！超局所層理論の第7回です．今回はGoresky・MacPhersonによるstratifiedモース理論を超局所層理論から見るとどのようになるかと，近接・消滅サイクルについて説明したいと思います．今回もいつものごとく証明はほとんど書いていませんので，ご了承ください．

前回までの高速おさらい

$\bfk$を体，$X$を$d$次元多様体とします．
第1回：$X$上の$\bfk$加群の層の複体$F \in \Db(\bfk_X)$に対して，そのコホモロジーが伝播しない余方向として層のマイクロ台$\MS(F)$という$X$の余接束$T^*X$の錐状閉部分集合を定義しました．そして様々な層のマイクロ台がどうなっているのかを調べて，良い状況ではマイクロ台が層の形を強く制限することがあることも見ました．
第2回：層に対する様々な演算を施した後のマイクロ台を評価する方法について説明しました．またそれらを使って超局所切り落としという操作を定義しました．
第3回：マイクロ台は常に包合的であるという定理の主張を述べました．さらに，余接束$T^*X$の中のある部分集合上だけに注目する超局所的な見方を実現するために超局所圏を導入して，そこではマイクロ台が層の形を制限するという主張がより広く成り立つことも見ました．また超局所圏のHomを茎に持つような層$\mu hom$があったらうれしそうだという気持ちを説明しました．
第4回：$X$上の層$F$から法束$T_MX$上の層$\nu_M(F)$を作り出す特殊化という操作$\nu_M \colon \Db(\bfk_X) \to \Db_{\bbR_{>0}}(\bfk_{T_MX})$を法変形を使って定義して，切断が$M$の近傍で法方向に指定された開きがある開部分集合上の$F$切断の帰納極限だということを見ました．さらにベクトル束上の錐状層の圏とその双対ベクトル束上の錐状層の圏の圏同値を与えるFourier-Sato変換について説明して，特殊化のFourier-Sato変換として超局所化$\mu_M(F)$という余法束$T^*_MX$上の層を定義しました．これは超局所化函手$\mu_M \colon \Db(\bfk_X) \to \Db_{\bbR_{>0}}(\bfk_{T^*_MX})$を定めました．
第5回：超局所化に基づいて函手$\mu hom \colon \Db(\bfk_X)^{\op} \times \Db(\bfk_X) \to \Db_{\bbR_{>0}}(\bfk_{T^*X})$を定義しました．$\mu hom$は超局所化函手の一般化になっていて，$\mu hom$の台はマイクロ台で評価ができるので超局所圏からの函手を誘導することも見ました．$\mu hom$の最も重要な性質は，その茎が一点$p$での超局所圏$\Db(\bfk_X;p)$におけるHom集合を与えることでした．
第6回：$\mu$-stratificationという「良い条件を満たすstratification」という概念を使って実解析的多様体上の（弱）構成可能層の定義を与えて，それらの性質を見ました．また，層が弱構成可能であることとマイクロ台が劣解析的ラグランジュ錐状閉部分集合であることが同値であることを説明しました．これを使うと（弱）構成可能層が層の演算で閉じていることも分かりました．

今回は以降$X$を実解析的多様体とします（あとで複素多様体にします）．また，$\pi$で余接束$T^*X \to X$をあらわして$0_X$または単に$X$でそのゼロ切断をあらわします．

Stratifiedモース理論と超局所層理論

Stratifiedモース理論はモース理論をstratified空間に拡張するもので，Goresky-MacPersonらによって詳しく研究されました．Stratifiedモース理論はstratified空間$S$上の「モース函数」が与えられたときに，その情報から$S$のトポロジーの情報を得ることが目的です．これを非形式的に少しだけ説明します．

$S$を$X$の部分集合として，$\mu$-staratification $X=(\bigsqcup_{\alpha \in A} S_\alpha) \sqcup (X \setminus S)$が与えられているとします．この$S$を以降は$X$に埋め込まれたstratified空間と呼ぶことにします．$S$は一般には特異空間なので，$x_0 \in S_\alpha \subset S$に対して$T_{x_0} S$以外にも$x_0$$S$に接している空間を考えることができます．$x_0$に収束するあるstratum$S_\beta$内の点列$x_i$に対して，$Q=\lim_{x \to x_0} T_{x_i} S_\beta$を$x_0$における一般化接空間と呼ぶことにしましょう．Stratified空間$S$上のstratifiedモース函数$\tilde{f} \colon S \to \bbR$とは次の4条件を満たすことをいいます：
(1) $\tilde{f}$はある$C^\infty$級函数$f \colon X \to \bbR$の$S$への制限$f|_S$である．
(2) 各stratum $S_\alpha$への制限$f|_{S_\alpha}$はモース函数である．
(3) 各臨界点$x_0 \in S_\alpha$と$T_{x_0}S_\alpha$と異なる$x_0$における任意の一般化接空間$Q$に対して，$df(Q) \neq 0$である．

以降は$X$全体で定義された函数$f$を最初から扱う方が都合が良いので，$f|_S$が$S$上のstratifiedモース函数であるとき$f$を$S$に関するstratifiedモース函数と呼んでしまいます．Stratifiedモース理論は，stratifiedモース函数$f \colon X \to \bbR$に対して$S$の劣位集合$S_{< c}=\{x \in S \mid f(x)< c \}$のトポロジー変化をとらえることが目的です．特に，臨界点$x_0$に対して$S_{< f(x_0)+\varepsilon}$が$S_{< f(x_0)-\varepsilon}$に何を貼り付けて得られるかを記述するものをモースデータと呼んで，これを調べていました．通常のモース理論では臨界点でのモース指数が$\lambda$のときは，モースデータはハンドルの貼り付けを意味する$(D^\lambda \times D^{d-\lambda}, \partial D^\lambda \times D^{d-\lambda})$です．

さて，Stratifiedモース理論の主定理は標語的には次のようなものです．

モースデータ$=$接モースデータ$\times$法モースデータ

ここで，接モースデータ (tangential Morse data) とは$S_\alpha$上のモース関数$f|_{S_\alpha}$の通常のモースデータのことです．また，法モースデータ (normal Morse data) は$S_\alpha$と一点$x_0$において横断的に交わる$X$の部分多様体$N$を取って，$N$内の$x_0$の近傍上でモースデータを考えたものです．このような部分多様体$N$は法スライス (normal slice) と呼ばれたりします．以下では上で標語的に述べたstratifiedモース理論の主定理のコホモロジーに関する主張が，超局所層理論を通してどのように解釈されるかを説明します．

層理論の観点では$S$のコホモロジーを調べたいので，$S$上の定数層を$X$上にゼロ拡張した$\bfk_S \in \Db(\bfk_X)$を考えることになります．このとき，$\bfk_S$のマイクロ台に関して
$$ \MS(\bfk_S) \subset \bigsqcup_{\alpha \in A} T^*_{S_\alpha}X =: T^*_S X $$
が成り立ちます．定義をよく考えると，$f \colon X \to \bbR$が$S$に関するstratifiedモース函数であることは$df$のグラフ$\Gamma_{df} \subset T^*X$が$T^*_SX$の非特異部分（その点の近傍で部分多様体となっている点全体）と横断的に交わることと同値であることが分かります．つまり$T^*_SX$を使ってstratifiedモース函数は超局所的な条件で記述できました．それではモースデータは層理論では何でしょうか？これは第1回でマイクロ台を導入した際にも説明したように，超局所的な障害$\RG_{\{f \ge f(x_0)\}}(\bfk_S)_{x_0}$のことです．実際，十分小さい$\varepsilon>0$に対して（これが取れることはSard型の定理から従う），完全三角
$$ \RG_{\{f \ge f(x_0) \}}(\bfk_S)_{x_0} \to \RG(S_{< f(x_0)+\varepsilon};\bfk_S) \to \RG(S_{< f(x_0)-\varepsilon};\bfk_S) \to \RG_{\{f \ge f(x_0) \}}(\bfk_S)_{x_0}[1] $$
が得られるからです．

上で説明した$\RG_{\{f \ge f(x_0) \}}(\bfk_S)_{x_0}$は，コホモロジーの情報に限ってもstratifiedモース理論のモースデータよりも少ない情報しか持っていない．モースデータはどこに張り付けるかも記述するが，相対コホモロジーだけではその情報がないからである．

さて，これまでの説明で層理論的には臨界点$x_0 \in S_\alpha$におけるモースデータはマイクロ台の定義にも現れた超局所的な障害$\RG_{\{f \ge f(x_0)\}}(\bfk_S)_{x_0}$に対応することが分かりました．特に，接モースデータは$\RG_{\{f \ge f(x_0)\}}(\bfk_{S_\alpha})_{x_0}$です．よって，層理論的に法モースデータは何に対応するかに興味がありますが，我々は層を法方向に変形する道具を既に持っています．それが第4回で説明した特殊化という操作でした．特殊化を使うと法スライスに対応する層理論的対象は$\nu_{S_\alpha}(\bfk_S)|_{(T_{S_\alpha}X)_{x_0}}$となると予想されます．こうして超局所層理論によるstratifiedモース理論の主定理の解釈は以下のように述べられます．

Stratifiedモース理論の超局所層理論による解釈

$S=\bigsqcup_{\alpha \in A}S_\alpha$を$X$に埋め込まれたstratified空間，$f \colon X \to \bbR$を$S$に関するstratifiedモース函数とする．$p_0 \in \Gamma_{df} \cap T^*_SX$として，$x_0:=\pi(p_0) \in S_\alpha=:M$を臨界点とする．$F:=\bfk_S \in \Db(\bfk_X)$とおく．
(i) $p_0$における超局所圏$\Db(\bfk_X;p_0)$において，同形$F \simeq \mu_{M}(F)_{p_0} \otimes \bfk_{M}$が成り立つ．
(ii) 同形
$$ \RG_{\{ f \ge f(x_0) \}}(F)_{x_0} \simeq \RG_{\{ f \ge f(x_0) \}}(\bfk_{M})_{x_0} \otimes \RG_{\{ v \in (T_{M}X)_{x_0} \mid \langle p_0, v \rangle \ge 0 \}}\left((T_{M}X)_{x_0};\nu_{M}(F)|_{(T_{M}X)_{x_0}} \right) $$
が成り立つ．

概略

(i)：$p_0$の近傍で$\MS(F) \subset T^*_{M}X$であるから，第3回の命題3(ii)により$V \in \Db(\bfk)$が存在して$\Db(\bfk_X;p_0)$において$F \simeq V_{M}$が成り立つ．一方で$\mu_{M}(V_{M}) \simeq V_{T^*_{M}X}$であることと超局所化の$p_0$での茎は$\Db(\bfk_X;p_0)$だけによることから，$V \simeq \mu_{M}(F)_{p_0}$が成り立つ．

(ii)：第4回の定理5(ii)から，$\mu_M(F)_{p_0} \simeq \RG_{\{ v \in (T_{M}X)_{x_0} \mid \langle p_0, v \rangle \ge 0 \}}\left((T_{M}X)_{x_0};\nu_{M}(F)|_{(T_{M}X)_{x_0}} \right)$であることがチェックできる．よって，結論は(i)の同形から従う．

上の命題の(ii)の同形は，コホモロジーに関してはモースデータ$\RG_{\{ f \ge f(x_0) \}}(F)_{x_0}$が接モースデータ$\RG_{\{ f \ge f(x_0) \}}(\bfk_{M})_{x_0}$と法モースデータ$\RG_{\{ v \in (T_{M}X)_{x_0} \mid \langle p_0, v \rangle \ge 0 \}}\left((T_{M}X)_{x_0};\nu_{M}(F)|_{(T_{M}X)_{x_0}} \right)$に分解されていることを述べています．この層理論的な解釈は，法スライスを取って議論しなくても特殊化によって標準的に層を法束上に錐化でき，記述が簡単になるという利点もあると思われます．

モース理論には他にも

臨界値を越えない限りホモトピー型が変わらない，
モース指数はモースデータの（コ）ホモロジーが唯一現れる次元（モース指数の（コ）ホモロジー的特徴づけ）

という重要な命題がありました．明らかに超局所モースの補題（第1回の定理3）は一つ目のコホモロジーに関する層理論的な一般化です．二つ目に関しては，複素解析的多様体に対しては交叉（コ）ホモロジー (intersection (co)homology) を使ったstratifiedな一般化があるのですが，ここでは詳しくは紹介しないことにします．興味がある方は参考文献に挙げるstratifiedモース理論に関する文献を参照してください．

構成可能層の近接・消滅サイクル

第4回で特殊化$\nu_M$・超局所化$\mu_M$という操作を導入しましたが，全てが複素の状況だとこれらの操作を別のやり方で定式化することができ，特異点論などの分野でよく現れます．ここではそれらの操作である近接・消滅サイクル函手を導入して，これまで説明した超局所層理論とのつながりを説明します．

$\bbC$-構成可能層

前回説明した構成可能層は実解析的多様体上のものでしたが，複素多様体上ではその複素構造に応じた構成可能層を考えることができます．応用上よく現れるのはこちらの複素的な構成可能層の方で下の説明でも必要なので，これについて簡単に説明します．

以下では$X$を$N$次元の複素多様体とします．このとき，$T^*X$には$\bbC^\times$の作用が入ります．$T^*X$の閉解析的部分集合が錐状であることと$\Lambda$が$\bbC^\times$作用で不変であることは同値であることがチェックできます．また，$X$の$\mu$-stratification $X=\bigsqcup_{\alpha \in A} X_\alpha$が複素$\mu$-stratificationであるとは各$X_\alpha$が$X$の複素部分多様体となることをいいます．すると，弱$\bbR$-構成可能層の特徴づけの類似として次が得られます．

複素版の弱構成可能層の超局所的特徴づけ

$F \in \Db(\bfk_X)$に対して次の条件は同値である：
(1) ある複素$\mu$-stratification $X=\bigsqcup_{\alpha \in A} X_\alpha$が存在して任意の$n \in \bbZ$と$\alpha \in A$に対して$H^n(F)|_{X_\alpha}$が局所定数層となる．
(2) $\MS(F)$は$T^*X$の解析的ラグランジュ錐状閉部分集合である．
(3) $F \in \DbwRc(\bfk_X)$であり，$\MS(F)$は$\bbC^\times$の作用で不変である．

（弱）$\bbC$-構成可能層

$F \in \Db(\bfk_X)$とする．
(i) $F$が弱$\bbC$-構成可能であるとは$F$が上の定理の同値な条件を満たすことをいう．弱$\bbC$-構成可能層からなる$\Db(\bfk_X)$の充満部分圏を$\DbwCc(\bfk_X)$であらわす．
(ii) $F$が弱$\bbC$-構成可能であり，さらに任意の$x \in X$と$n \in \bbZ$に対して$H^n(F)_x$が有限次元ベクトル空間となるとき，$F$は$\bbC$-構成可能であるという．$\bbC$-構成可能層からなる$\Db(\bfk_X)$の充満部分圏を$\DbCc(\bfk_X)$であらわす．

例えば複素多様体$X$の解析的部分集合$V$に対して$\bfk_V$は$\bbC$-構成可能層となります．定理の弱構成可能性の超局所的特徴づけと超局所的層理論のモース理論的な議論を用いることで，前回と同様に（弱）$\bbC$-構成可能層の圏は層の演算で閉じていることも示すことができます．

近接・消滅サイクル

ここではまず近接・消滅サイクルを天下り的に定義して，あとでミルナーファイバーや特殊化・超局所化とのつながりを見ていくことにしましょう．

$X$を$N$次元の複素多様体として$f \colon X \to \bbC$を正則函数とします．$Y:=f^{-1}(0)$として，$i \colon Y \hookrightarrow X$で埋め込みをあらわします．$p \colon \tilde{\bbC}^*=\bbC \to \bbC, t \mapsto \exp(2\pi\sqrt{-1}t)$を$\bbC^*=\bbC \setminus \{0\}$の普遍被覆と埋め込みの合成として，$\tilde{X}^*:=X \times_\bbC \tilde{\bbC}^*$と定めます．$\tilde{p} \colon \tilde{X}^* \to X$を$p$に付随する射影とすると，次の四角がファイバー積になる図式が得られます：
$$ \xymatrix{ & \tilde{X}^* \ar[r] \ar[d]_-{\tilde{p}} & \tilde{\bbC}^* \ar[d]^-{p} \\ Y \ar@{^{(}->}[r]_-{i} & X \ar[r]_-{f} & \bbC. } $$
$\tilde{p}$のファイバーは$0$次元なので$\tilde{p}_!$は完全函手となることに注意しましょう．

近接サイクル

$F \in \Db(\bfk_X)$に対して
$$ \psi_f(F):=i^{-1} R\tilde{p}_* \tilde{p}^{-1} F \in \Db(\bfk_{Y}) $$
と定めて，$F$の$f$による近接サイクル (nearby cycle) と呼ぶ．

$\psi_f \colon \Db(\bfk_X) \to \Db(\bfk_Y)$は近接サイクル函手と呼ばれます．随伴から自然な射$i^{-1}F \to \psi_f(F)$が定まることにも注意しましょう．基本的には消滅サイクルはこの自然な射の写像錐のことで，そのように定義している本も多いのですが，ここではSheaves on Manifoldsに従い，より具体的に定義するやり方を取ります．

$\tilde{p}$に関しては$\tilde{p}^! \simeq \tilde{p}^{-1}$が成り立つことが分かるので，次の同形が成り立ちます：
\begin{align} R\tilde{p}_* \tilde{p}^{-1} F & \simeq R\tilde{p}_* \cRHom(\bfk_{\tilde{X}^*}, \tilde{p}^{-1} F) \\ & \simeq \cRHom(\tilde{p}_! \bfk_{\tilde{X}^*}, F) \\ & \simeq \cRHom(f^{-1}p_! \bfk_{\tilde{\bbC}^*},F). \end{align}
ここで最後の同形には固有基底変換（層理論第6回命題11）を用いました．この同形を通すと，$\tilde{\bbC}^*=\bbC$における$1 \in \bbZ$の作用によって$p_! \bfk_{\tilde{\bbC}^*}$の自己同形が誘導され，これにより$\psi_f(F)$の自己同形$M_\psi \colon \psi_f(F) \to \psi_f(F)$が引き起こされます．この自己同形$M_\psi$は$\psi_f(F)$のモノドロミーと呼ばれます．さて，上の同形を睨んで次の$\bfk_\bbC$が$0$次に位置する複体$K$を考えます：
$$ K : 0 \to p_! \bfk_{\tilde{\bbC}^*} \to \bfk_\bbC \to 0. $$
ここで微分射は$ p_! \bfk_{\tilde{\bbC}^*} \simeq p_! p^! \bfk_\bbC \to \bfk_\bbC$なる射です．

消滅サイクル

$F \in \Db(\bfk_X)$に対して
$$ \phi_f(F):=i^{-1} \cRHom(f^{-1}K,F) \in \Db(\bfk_{Y}) $$
と定めて，$F$の$f$による消滅サイクル (vanishing cycle) と呼ぶ．

$\phi_f \colon \Db(\bfk_X) \to \Db(\bfk_Y)$は消滅サイクル函手と呼ばれます．上で見た$p_! \bfk_{\tilde{\bbC}^*}$の自己同形と$\bfk_\bbC$の恒等射で$K$の自己同形が定まって，これによって$\phi_f(F)$のモノドロミー自己同形$M_\phi \colon \phi_f(F) \to \phi_f(F)$が引き起こされます．

消滅サイクルのシフトのずれ

多くの文献では，ミルナーファイバーとの関係で上で定義した$\phi_f(F)$の$1$次シフト$\phi_f(F)[1]$を消滅サイクルとしているものが多い．ここでのシフトはSheaves on Manifoldsに従っており，これは後で見る超局所化との同形にシフトが現れないようにするためだと思われる．

構成から二つの完全三角
\begin{align} & \bfk_\bbC \to K \to p_! \bfk_{\tilde{\bbC}^*}[1] \to \bfk_\bbC[1], \\ & p_! \bfk_{\tilde{\bbC}^*}[1] \to K \to \bfk_{\{0\}} \to p_! \bfk_{\tilde{\bbC}^*}[2] \end{align}
が存在することがチェックできます．ここから$F \in \Db(\bfk_X)$に対して二つの完全三角
\begin{align} & \psi_f(F)[-1] \overset{\mathrm{can}}{\to} \phi_f(F) \to i^{-1}F \to \psi_f(F), \\ & i^!F \to \phi_f(F) \overset{\mathrm{var}}{\to} \psi_f(F)[-1] \to i^!F[1] \end{align}
が存在して，
$$ \begin{cases} \mathrm{can} \circ \mathrm{var} = 1-M_\phi, \\ \mathrm{var} \circ \mathrm{can} = 1-M_\psi \end{cases} $$
が成り立ちます．

さて，これまでは天下り的に近接・消滅サイクルを導入しましたが，これらはミルナーファイバーとそれに付随するモノドロミーに密接に結びついています．それを説明するためにミルナーファイバーについて少しだけ説明しましょう．$X$は$\bbC^N$に埋め込まれているとして，$f \colon X \to \bbC$を$0$でない正則函数，$x \in f^{-1}(0)$とします．このとき，Milnorの結果によると，ある$0 < \delta \ll \varepsilon \ll 1$が存在して，$f$の制限
$$ X \cap B(x;\varepsilon) \cap f^{-1}(D^*(0;\delta)) \to D^*(0;\delta) $$
はファイバーバンドルになります．ここで$B(x;\varepsilon)$は$\bbC^N$の$x$を中心とする半径$\varepsilon$の開球で，$D^*(0;\delta)$は$\bbC$の原点$0$を中心とする半径$\delta$の穴あき円盤をあらわします．このファイバーをここでは$\mathrm{MF}_x$と書いてミルナーファイバーと呼びます（一般には$F_x$と書かれますが，層の茎と区別できないため別の記号を使います）．$D^*(0;\delta)$を一周回ることでミルナーファイバーのコホモロジーにミルナーモノドロミーと呼ばれる自己同形
$$ M_n \colon H^n(\mathrm{MF}_x;\bfk) \to H^n(\mathrm{MF}_x;\bfk) $$
が定まります．概念的には図1を参照してください．実は$x$が正則函数$f \colon \bbC^N \to \bbC$の孤立特異点のときにはミルナーファイバーは$S^{N-1}$の有限個のブーケ$S^{N-1} \vee \dots \vee S^{N-1}$とホモトピー同値となることがミルナーによりモース理論を用いて示されています．このときは，ミルナーファイバーのコホモロジーも簡単になるのでミルナーモノドロミーに関してもさまざまな結果が知られています．非孤立特異点を持つ場合にはミルナーファイバーのコホモロジーとモノドロミーを調べる問題は非常に難しいですが，一般に次の近接・消滅サイクルとの関係があり，これを通して部分的な情報が得られています．

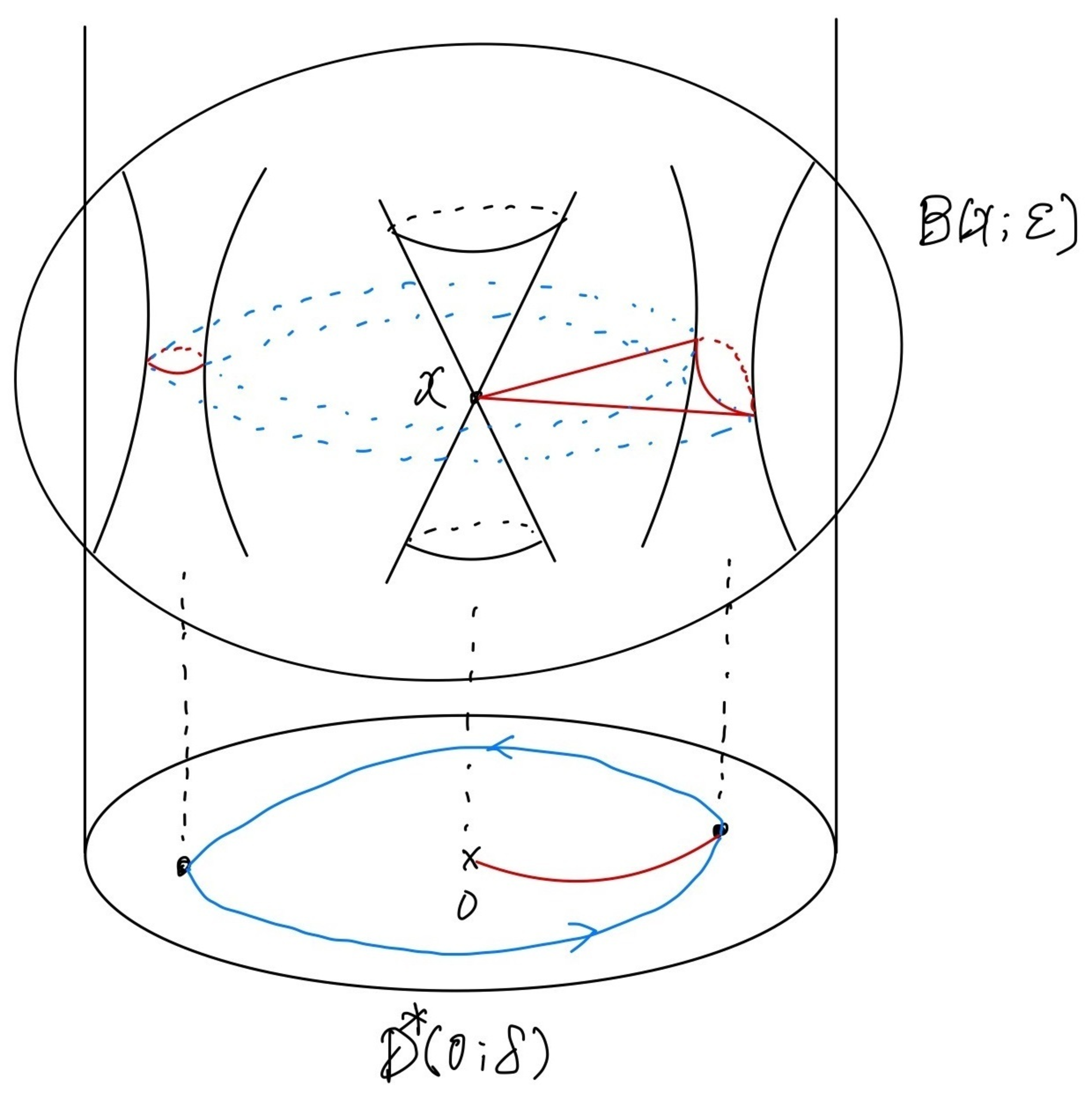ミルナーファイバー・ミルナーモノドロミーの概念図

近接・消滅サイクルとミルナーファイバーのコホモロジーとの関係

$x \in f^{-1}(0)$に対して，同形
$$ H^n(\mathrm{MF}_x;\bfk) \simeq H^n(\psi_f(\bfk_X)), \quad \tilde{H}^n(\mathrm{MF}_x;\bfk) \simeq H^{n+1}(\phi_f(\bfk_X)) $$
が成り立つ．ここで$\tilde{H}^n$は$n$次の簡約コホモロジーである．さらに，これらの同形は両辺のモノドロミーと両立する．すなわち同形はミルナーモノドロミーと近接・消滅サイクルのモノドロミーと可換である．

二つ目の同形でコホモロジー側の次数が$n+1$となっていますが，ここを$n$にするために多くの本では上で定義したSheaves on Manifolds流の消滅サイクルのシフトと次数が$1$ずれています．上のミルナーファイバーとの関係は近接・消滅サイクルの名前の由来を明らかにします．孤立特異点の状況を考えれば，近接サイクル函手の茎は特異ファイバーの近くのミルナーファイバーのコホモロジーを与えていて，消滅サイクル函手の茎はミルナーファイバーのサイクルで特異ファイバーに送ると消滅してしまうものをあらわしています（図1を参照）．実は近接・消滅サイクル函手はD加群の側にも定義されて，リーマン・ヒルベルト対応によって構成可能層の近接・消滅サイクル函手と両立しています．こうしてミルナーファイバーに関する研究にもD加群が有効に用いられています．

最後に$Y=f^{-1}(0)$が非特異の場合に近接・消滅サイクルと特殊化・超局所化との関係を主張だけ述べて終わりにしましょう．$Y=f^{-1}(0)$が非特異の場合は$df$によって函数$\tilde{f} \colon T_YX \to \bbC$が定まります．$s \colon Y \to T_YX$を$\tilde{f}^{-1}(1)$で定まる$T_YX$の切断，$s' \colon Y \to T^*_YX$を$df$で定まる$T^*_YX$の切断とします．

近接・消滅サイクルと特殊化・超局所化との関係

$Y=f^{-1}(0)$が非特異であると仮定して，$s,s'$を上のように定める．このとき，$F \in \DbwCc(\bfk_X)$に対して，同形
$$ \psi_f(F) \simeq s^{-1} \nu_Y(F), \quad \phi_f(F) \simeq s'^{-1} \mu_Y(F) $$
が成り立つ．

証明は面倒なので述べませんが，特殊化・超局所化が$\bbC^\times$作用で不変であることを使う必要があることだけを注意しておきます．上の命題の二つ目の同形から，弱$\bbC$-構成可能層に対してはマイクロ台が消滅サイクルから回復できることが分かります．

マイクロ台と消滅サイクル

$F \in \DbwCc(\bfk_X)$とする．このとき，$p \in T^*X$に対して次の2条件は同値である：
(1) $p \not\in \MS(F)$.
(2) $p$のある開近傍$U$であって任意の$x \in X$と任意の$x$の近傍で定義された$f(x)=0, df(x) \in U$を満たす正則函数$f$に対して，$\phi_f(F)_x \simeq 0$である．