絡分で三角形演算子を連続にする

挨拶

こんにちは！！Nappleです
この記事では以前記事にした２つの概念「三角形演算子」と「絡分」を組み合わせて遊びます。過去の内容は以下を参照してください。

問題提起

三角形演算子は総和と総乗を使って定義されます。
また、絡分によって総乗$\gprod{}{}{}$が連続になりました。

ということは、
積分と絡分を使って三角形演算子も連続にできるのではないでしょうか。

三角形演算子と絡分の復習

まず、本題に入る前に復習をしておきます。
三角形演算子（と超三角形演算子）の定義を確認しましょう。

イメージとしては以下のように、長さ$k$の範囲をずらしながら掛けて足す感じです。
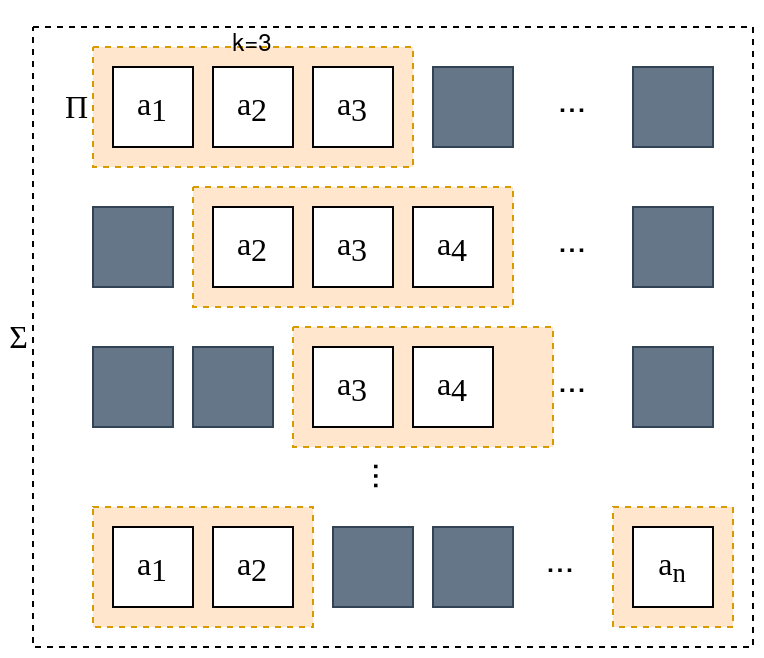三角形演算子のイメージ

また、絡分の定義は以下です。

これは総和と総乗の関係
$$ \prod a_i = p ^{\sum \log_p a_i} $$
に従って定義したものです。
なお、この$p$には何を入れても同値になるので、今回は$p=e$として考えます。

雑にやっていく

超三角形演算子の定義式の総和と総乗をそのまま積分と絡分に置き換えてみます。
$$ \begin{eqnarray} \genprodsum{i=a}{b}{k}{a_i} &=& \gsum{i=a}{b}{\gprod{j=i}{i+k}{a_{(j-1)\%n+1}}} \\ &\rightarrow& \int_a^b \left\{ \exp \int_a^x \ln f(t) dt \cdot \exp \int_{x+(b-a)-k}^b \ln f(t) dt \right\} dx \\ &=& \int_a^b \exp \left( \int_a^x \ln f(t) dt + \int_{x+(b-a)-k}^b \ln f(t) dt \right) dx \\ &=:& \genprodsum{x \in [a,b]}{}{k}{f(x)} \end{eqnarray} $$
できた。

確かめる

連続超三角形演算子が離散のときの性質を引き継いでくれると嬉しいんですよね〜

$\genprodsum{i=1}{n}{k}{c}$に関して

例えば、$ \genprodsum{i=1}{n}{k}{c} = nc^{k} $ を連続版でも考えてみましょう。($c$は定数)

$$ \begin{eqnarray} \genprodsum{t \in [0,x]}{}{k}{c} &=& \int_0^x \exp \left( \int_0^t \ln c ds + \int_{t+x-k}^x \ln c ds \right) dt \\ &=& \int_0^x \exp \ln c \left( [s]_0^t + [s]_{t+x-k}^x \right) dt \\ &=& \int_0^x \exp (k \ln c) dt \\ &=& xc^k \end{eqnarray} $$

なんと！これで$x=n$のとき離散版のときと一致しますね。嬉しい〜

$ \genprodsum{i=1}{n}{}{i}$に関して

同様に$ \genprodsum{i=1}{n}{}{i} = n!\gsum{i=1}{n}{\frac{1}{i}} $についても連続版で考えてみましょう。

$$ \begin{eqnarray} \genprodsum{x \in [a,b]}{}{k}{x} &=& \int_a^b \exp \left( \int_a^x \ln t dt + \int_{x+b-a-k}^b \ln t dt \right) dx \\ &=& \int_a^b \exp \left( [t(\ln t - 1)]_a^x + [t(\ln t - 1)]_{x+b-a-k}^b \right) dx \\ &=& \int_a^b \exp \left( x\ln x - x - a\ln a + a + b\ln b - b - (x+b-a-k)\ln (x+b-a-k) + (x+b-a-k) \right) dx \\ &=& \int_a^b \frac{b^b x^x}{a^a e^k (x+b-a-k)^{x+b-a-k}} dx \\ &=& \frac{b^b}{a^a e^k} \int_a^b \frac{x^x}{(x+b-a-k)^{x+b-a-k}} dx \\ \end{eqnarray} $$
となり、これは直接はまあ解けない（本当ですか？）のですが
$a,b,k$を具体的な値に固定して計算してみましょう。

元の$\genprodsum{i=1}{n}{}{i}$←この式に対応する値を考えると、
前提として$\genprodsum{i=1}{n}{}{i} = \genprodsum{i=1}{n}{n-1}{i}$なので、範囲は$[0,x]$、$k=x-1$として計算します。

$$ \begin{eqnarray} \genprodsum{t \in [0,x]}{}{\space }{x} &=& \frac{x^x}{0^0 e^x} \int_0^x \frac{t^t}{(t+x-0-(x-1))^{t+x-0-(x-1)}} dt \\ &=& \frac{x^x}{e^x} \int_0^x \frac{t^t}{(t+1)^{t+1}} dt \\ &=& \left( \frac{x}{e} \right)^x L(x) \\ \end{eqnarray} $$

ここで以前の記事から、
前半の$\left( \frac{x}{e} \right) ^x $は$x$の絡分、つまり階乗に対応するものであるとわかっています。

また、後半の積分$L(x) = \int_0^x \frac{t^t}{(t+1)^{t+1}}$は解けなさそうなので
Desmos先生に数値計算してもらうと以下のようになります。
赤:$L(x)$ 緑:$\log_{10} x$のグラフ

オーダーとしては対数に近いみたいですね。

これで、

$$ \genprodsum{i=1}{n}{\space }{i} = n!\gsum{i=1}{n}{\frac{1}{i}} $$
と
$$\genprodsum{t \in [0,x]}{}{\space }{x} = \frac{x^x}{e^x} \int_0^x \frac{t^t}{(t+1)^{t+1}} dt \sim x!\ln x$$
も、一致こそしないもののなんとなーく対応していることがわかりました。
まだ色々と検討点がありそうで嬉しいですね。

まとめ

今回は連続な総乗である絡分を応用して、三角形演算子の連続化に挑戦してみました。
具体例として$\genprodsum{t \in [0,x]}{}{\space }{c}$と$\genprodsum{t \in [0,x]}{}{\space }{x}$を計算してみると、
離散な場合とある程度対応していることもわかりました。

今回の結果から絡分および連続版の三角形演算子はなんとなく妥当な定義の一つかなと感じています。追ってさらなる検討を行いたいですね。

記事は以上です。
それではまた〜