Steinerシステム - アフィン平面
- Fisher不等式
- 自己同型群
- アフィン平面
-
Steinerトリプルシステム
- Mathieu群 $M_{11}$と$M_{12}$
Steinerシステムとしてのアフィン平面
証明
(1)$\Longrightarrow$(2)
§1-定理1
から
\begin{eqnarray}
r=\frac{k^2-1}{k-1}=k+1
\end{eqnarray}
(2)$\Longrightarrow$(3)
§1-定理3
から$b=\dfrac{k^2(k^2-1)}{k(k-1)}=k(k+1)$
(3)$\Longrightarrow$(1)
§1-定理3
から
\begin{eqnarray}
bk&=&vr\\
k^2(k+1)&=&v\frac{v-1}{k-1}\\
v^2-v-k^2(k^2-1)&=&0\\
(v-k^2)(v+k^2-1)&=&0\\
v&=&k^2\hspace{2mm}(\because v+k^2>2)
\end{eqnarray}
(2)$\Longrightarrow$(4)
$B=\lbrace x_1,x_2,\cdots,x_k\rbrace$とおくと, 組$(\alpha,x_i)\hspace{2mm}(1\leq i\leq k)$は異なる$k$個のブロックに含まれている. なぜなら, $(\alpha,x_i)$と$(\alpha,x_j)\hspace{2mm}(i\neq j)$が$B$と異なる同じブロックに含まれているとすると, そのブロックは$(x_i,x_j)$を含むことになるが,
定義
からこれは矛盾する. したがって, $\alpha\notin B$は$k$個の異なるブロックに含まれる. いま, $r=k+1$を仮定していたのだから, これら$k$個のどのブロックとも異なり, $\alpha$を含むブロックが一意に定まる. そして, このブロックは明らかに$B$と共通部分を持たない.
(4)$\Longrightarrow$(2)
上と同様の議論から, $\alpha\notin B$は$k$個の異なるブロックに含まれ, これらのブロックは$B$と共通部分を持つ. いま, $B$とは共通部分を持たない$\alpha$を含むブロックが一意に定まると仮定したため, $\alpha$を含むブロックの個数は$k+1$個である. $\alpha$を任意に取ったので, $r=k+1$.
(1)～(4)の同値な条件を満たすSteinerシステムをアフィン平面と呼ぶ. アフィン平面に関する議論は, $\Omega$の元を平面あるいは空間上の点, $\mathcal{B}$の元, 即ちブロックを直線だと解釈すると理解の助けとなる. 例えば, (4)の条件
\begin{eqnarray}
{}^{\forall}B\in\mathcal{B},{}^{\forall}\alpha\in\Omega\backslash B,{}^{\exists!}B'\in\mathcal{B}\hspace{2mm}s.t.\hspace{2mm}\alpha\in B',B\cap B'=\varnothing
\end{eqnarray}
は, ある直線$B$とその直線上にない1点$\alpha$を選んできたとき, $\alpha$を通る直線は一意に定まり, なおかつその直線は$B$と平行であると読み替えられる. これらのことから, 以下ではアフィン平面のブロックを直線と呼ぶことにする.
無論幾何分野のアフィン空間と関係はあるが, ここではアフィン平面はあくまでSteinerシステムの特殊な場合であって, 簡単な集合論の言葉で完結する.
平行類
証明
(1)(2)
類$\mathcal{P}$を以下のように構成する.
$B_0\in\mathcal{B}$と$\alpha_1\in\Omega\backslash B_0$を取ると, 定理1から$\alpha_1\in B_1,B_0\cap B_1=\varnothing$を満たす$B_1\in\mathcal{B}$が一意に存在する. 和$\bigcup_{i=0}^{1}B_i$に関して帰納法を用いる.
$l\geq2$に対して, $\bigcup_{i=0}^{l}B_i$が存在すると仮定する.
$\bigcup_{i=0}^{l}B_i\neq\Omega$とすると, 定理1から$\alpha_{l+1}\in\Omega\backslash\bigcup_{i=0}^{l}B_i$が取れ, $\alpha_{l+1}\in B_{l+1},B_i\cap B_{l+1}=\varnothing$を満たす$B_{l+1}\in\mathcal{B}$が一意に存在する.
ゆえに, $\bigcup_{i=0}^{l+1}B_i$が存在する.
$\bigcup_{i=0}^{l}B_i=\Omega$であれば, $B_i,B_j\subset\bigcup_{i=0}^{l},B_i\cap B_j=\varnothing$であるから
\begin{eqnarray}
\sum_{i=0}^{l}|B_i|&=&|\Omega|\\
k(l+1)&=&k^2\\
l&=&k-1
\end{eqnarray}
より$\mathcal{P}$は$k$本の直線を持つ.
(3)
直線と類$B\in\mathcal{P}$に対して, $B\cap B'\neq\varnothing$を満たす$B'\in\mathcal{P}$が存在すると仮定する.
上の議論から類$\mathcal{P}$はすべての元を過不足なく含んでいるため, $\Omega$の元をひとつ決めれば, $\mathcal{P}$の中の直線でその元を含むものが一意に定まる. $x\in B'$に対して, $x$を含む$\mathcal{P}$の直線を$B_x$とすると, $B,B_x\in\mathcal{P}$より$B\cap B_x=\varnothing$.
$x\notin B$に対して, $x$を含む直線が一意に定まったのだから, $B_x=B'$.
しかし, これは$B'\in\mathcal{P}'$に反するため, $B\cap B'=\varnothing$.
例. 位数3のアフィン平面
$S=S(2,k,k^2)$がアフィン平面のとき, $k$を位数という.
$t< k< v$の仮定
の下では最小のアフィン平面である$S(2,3,9)$は次のように構成できる.
\begin{eqnarray}\left\{\begin{array}{ll}
(\overline{x-c},x,\overline{x+c}) & (c=1,2,4,x=1,4,7)\\
(\overline{1+c'},\overline{4+c'},\overline{7+c'}) & (c'=0,1,2)
\end{array}\right.\end{eqnarray}
$c$の値が平行類の分割を表していて, $\overline{a}$は$a$を9で割った余りである. 明示的に書けば,
\begin{eqnarray}
(\overline{0},1,\overline{2})&=&(9,1,2)\hspace{3mm}(c=1,x=1)\\
(\overline{3},4,\overline{5})&=&(3,4,5)\hspace{3mm}(c=1,x=4)\\
(\overline{6},7,\overline{8})&=&(6,7,8)\hspace{3mm}(c=1,x=7)\\
(\overline{-1},1,\overline{3})&=&(8,1,3)\hspace{3mm}(c=2,x=1)\\
(\overline{2},4,\overline{6})&=&(2,4,6)\hspace{3mm}(c=2,x=4)\\
(\overline{5},7,\overline{9})&=&(5,7,9)\hspace{3mm}(c=2,x=7)\\
(\overline{-3},1,\overline{5})&=&(6,1,5)\hspace{3mm}(c=4,x=1)\\
(\overline{0},4,\overline{8})&=&(9,4,8)\hspace{3mm}(c=4,x=4)\\
(\overline{3},7,\overline{11})&=&(3,7,2)\hspace{3mm}(c=4,x=7)\\
(\overline{1},\overline{4},\overline{7})&=&(1,4,7)\hspace{3mm}(c'=0)\\
(\overline{2},\overline{5},\overline{8})&=&(2,5,8)\hspace{3mm}(c'=1)\\
(\overline{3},\overline{6},\overline{9})&=&(3,6,9)\hspace{3mm}(c'=2)
\end{eqnarray}
ただし, $9\coloneqq\overline{0}$としている. これは9次完全グラフ$K_9$における三角形の分割と解釈できる.
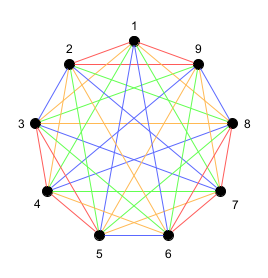辺彩色により平行類を分割している
基本的な性質
$S$を位数$k$のアフィン平面とする. このとき, 同一直線上にない3点を三角形, どの3点も同一直線上にない4点を四角形と呼び, 以下が成り立つ.
(1) 三角形の個数は$\dfrac{1}{6}k(k+1)(k^4-k^3-2k^2+2k-6)$
(2) 四角形の個数は$\dfrac{1}{24}k^2(k^2-1)(k^4-6k^2+5k-24)$
(3) 一つの四角形に4つの三角形が含まれる
(4) ある三角形は$k^2-3k+3$個の四角形に含まれている
証明
(1)
$k^2$個の点から3点を選ぶが, 同じ直線上に含まれている3つ組は除くため
\begin{eqnarray}
\mqty(k^2\\3)-k(k+1)=\frac{1}{6}k(k+1)(k^4-k^3-2k^2+2k-6)
\end{eqnarray}
(2)
$k^2$個の点から4点を選ぶが, 同じ直線上に含まれている4つ組, 直線上の3つ組と他の1点からなる4点は除くため
\begin{eqnarray}
\mqty(k^2\\4)-\mqty(k\\4)k(k+1)-k(k+1)(k^2-k)\\
=\frac{1}{24}k^2(k^2-1)(k^4-6k^2+5k-24)
\end{eqnarray}
(3)
四角形はどの3点も同一直線上にない4点から構成されているため, 4点から3点を任意に選べば三角形が得られる. よって, ある四角形に三角形は4つ含まれる.
(4)
三角形を取り, 他の1点を選んで4点を構成する方法は$k^2-3$通り.
しかし, 他の1点が三角形上の2点と同一直線上にあってはならないという制約が加わるため, ある三角形を含む四角形の個数は
\begin{eqnarray}
k^2-3-3(k-2)=k^2-3k+3
\end{eqnarray}
