Steinerトリプルシステム

ブロックデザイン,組合せ論

Fisher不等式

自己同型群

アフィン平面

Steinerトリプルシステム
1. STSの直積

Mathieu群 $M_{11}$ と $M_{12}$
1. S(2,3,9)の性質
2. S(3,4,10)の構成

構成したSteinerシステム

(2,3,7) , (2,3,9) , (2,3,13)NEW
(3,4,8)

STSの定義と存在条件

　 $S (Ω, B) = S (2, 3, v)$ の形のSteinerシステムを特にSteinerトリプルシステムと呼び, $S T S (v)$ や $S T S (Ω)$ と表記する. $S T S (7), S T S (9)$ はそれぞれ位数最小の射影平面とアフィン平面である.

定理

S T S (v)

が存在するための必要十分条件は,

v \equiv 1, 3 (m o d 6)

である.

証明　(Kirkman)

(必要)
§1-定理3 からブロックの個数は $\frac{v (v - 1)}{6}$ .
$v (v - 1)$ は偶数で, $v$ と $v - 1$ のいずれかが3の倍数であればブロックの個数は整数となる.
したがって, $v \equiv 1, 3 (m o d 6)$
(十分)
[i] $v \equiv 1 (m o d 6)$ のとき
$v = 6 t + 1$ とおき,
$\begin{array}{rcl} X & : = & {x_{1}, x_{2}, \dots, x_{2 t}} \\ Y & : = & {y_{1}, y_{2}, \dots, y_{2 t}} \\ Z & : = & {z_{1}, z_{2}, \dots, z_{2 t}} \end{array}$
により $v$ 点集合 $Ω$ を
$\begin{array}{r} Ω : = X \cup Y \cup Z \cup {α} \end{array}$
と定める.
次に, $[\begin{matrix} 1 & t + 1 & 2 & t + 2 & \dots & 2 t - 1 & t & 2 t \end{matrix}]$ を左にスライドして得られる $2 t \times 2 t$ のラテン方格
$\begin{array}{r} L_{e} : = [\begin{array}{c} 1 & t + 1 & 2 & t + 2 & \dots & 2 t - 1 & t & 2 t \\ t + 1 & 2 & t + 2 & 3 & \dots & t & 2 t & 1 \\ 2 & t + 2 & 3 & t + 3 & \dots & 2 t & 1 & t + 1 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋮ \\ 2 t - 1 & t & 2 t & 1 & \dots & t - 2 & 2 t - 2 & t - 1 \\ t & 2 t & 1 & t + 1 & \dots & 2 t - 2 & t - 1 & 2 t - 1 \\ 2 t & 1 & t + 1 & 2 & \dots & t - 1 & 2 t - 1 & t \end{array}] \end{array}$
を考える.
$l (i, j)$ を $L_{e}$ の $(i, j)$ 成分として, 定義から $l (i, j) = l (\overset{―}{i + 1}, \overset{―}{j - 1})$ .
ただし, $\overset{―}{p}$ は $p$ を $2 t$ で割った余りとする.
$j = i + k$ とすると,
$\begin{array}{rcl} l (i, j) & = & l (\overset{―}{i + 1}, \overset{―}{j - 1}) \\ = & (\overset{―}{i + 2}, \overset{―}{j - 2}) \\ = & \dots \\ = & l (\overset{―}{i + k}, \overset{―}{j - k}) \\ = & l (j, i) \end{array}$
より, $L_{e}$ は対称行列である.
$\begin{array}{rcl} l (i, i) & = & l (\overset{―}{i - 1}, \overset{―}{i + 1}) \\ = & l (\overset{―}{i - 2}, \overset{―}{i + 2}) \\ = & \dots \\ = & l (1, \overset{―}{2 i - 1}) \end{array}$
から, 対角成分は
$\begin{array}{r} l (i, i) = {\begin{cases} i & 1 \leq i \leq t \\ i - t & t + 1 \leq i \leq 2 t \end{cases} \end{array}$
と表される.
以上のことから,
$\begin{array}{r} {\begin{cases} (x_{i}, x_{j}, y_{l (i, j)}), (y_{i}, y_{j}, z_{l (i, j)}), (z_{i}, z_{j}, x_{l (i, j)}) & 1 \leq i, j \leq 2 t, i \neq j \\ (x_{i}, y_{l (i, i)}, z_{l (i, i)}) & 1 \leq i \leq t \\ (x_{i}, y_{l (i, i)}, α), (y_{i}, z_{l (i, i)}, α), (z_{i}, x_{l (i, i)}, α) & t + 1 \leq i \leq 2 t \end{cases} \end{array}$
のように3つ組を構成したとき, これらは $S T S (v) = S T S (6 t + 1)$ のブロックであることが簡単に確認できる.
[ii] $v \equiv 3 (m o d 6)$ のとき
$v = 6 t + 3$ とおき,
$\begin{array}{rcl} X & : = & {x_{1}, x_{2}, \dots, x_{2 t + 1}} \\ Y & : = & {y_{1}, y_{2}, \dots, y_{2 t + 1}} \\ Z & : = & {z_{1}, z_{2}, \dots, z_{2 t + 1}} \end{array}$
により $v$ 点集合 $Ω$ を
$\begin{array}{r} Ω : = X \cup Y \cup Z \end{array}$
と定める.
次に, $[\begin{matrix} 1 & t + 2 & 2 & t + 3 & \dots & t & 2 t + 1 & t + 1 \end{matrix}]$ を左にスライドして得られる $(2 t + 1) \times (2 t + 1)$ のラテン方格
$\begin{array}{r} L_{o} : = [\begin{array}{c} 1 & t + 2 & 2 & t + 3 & \dots & t & 2 t + 1 & t + 1 \\ t + 2 & 2 & t + 3 & 3 & \dots & 2 t + 1 & t + 1 & 1 \\ 2 & t + 3 & 3 & t + 4 & \dots & t + 1 & 1 & t + 2 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋮ \\ t & 2 t + 1 & t + 1 & 1 & \dots & 2 t - 1 & t - 1 & 2 t \\ 2 t + 1 & t + 1 & 1 & t + 2 & \dots & t - 1 & 2 t & t \\ t + 1 & 1 & t + 2 & 2 & \dots & 2 t & t & 2 t + 1 \end{array}] \end{array}$
を考える.
$l (i, j)$ を $L_{o}$ の $(i, j)$ 成分として, 定義から $l (i, j) = l (\overset{―}{i + 1}, \overset{―}{j - 1})$ .
ただし, $\overset{―}{p}$ は $p$ を $2 t + 1$ で割った余りとする.
[i]と同様に $L_{o}$ は対称行列で, $l (i, i) = l (1, \overset{―}{2 i - 1})$ だが,
$[\begin{matrix} 1 & t + 2 & 2 & t + 3 & \dots & t & 2 t + 1 & t + 1 \end{matrix}]$ の $i$ 列目の成分は $\overset{―}{2 i - 1}$ と書けるため, $l (i, i) = i$ が成り立つ.
以上より
$\begin{array}{r} {\begin{cases} (x_{i}, x_{j}, y_{l (i, j)}), (y_{i}, y_{j}, z_{l (i, j)}), (z_{i}, z_{j}, x_{l (i, j)}) & 1 \leq i, j \leq 2 t, i \neq j \\ (x_{i}, y_{l (i, i)}, z_{l (i, i)}) & 1 \leq i \leq t \end{cases} \end{array}$
のように3つ組を構成したとき, これらは $S T S (v) = S T S (6 t + 3)$ のブロックであることが簡単に確認できる.

例. $S T S (13)$ の構成

　Kirkmanの証明に沿って $S T S (13)$ を実際に構成する.
$13 = 6 \cdot 2 + 1$ であるから, $4 \times 4$ のラテン方格
$\begin{array}{r} [\begin{array}{c} 1 & 3 & 2 & 4 \\ 3 & 2 & 4 & 1 \\ 2 & 4 & 1 & 3 \\ 4 & 1 & 3 & 2 \end{array}] \end{array}$
を利用する. 13点集合 $Ω = {1, 2, \dots, 13}$ を次のように添え字付けしておく.
$\begin{array}{rcl} X & = & {x_{1} = 1, x_{2} = 2, x_{3} = 3, x_{4} = 4} \\ Y & = & {y_{1} = 5, y_{2} = 6, y_{3} = 7, y_{4} = 8} \\ Z & = & {z_{1} = 9, z_{2} = 10, z_{3} = 11, z_{4} = 12} \end{array}$
ラテン方格の非対角成分から
$\begin{array}{rcl} (x_{1}, x_{2}, y_{3}) & , (x_{1}, x_{3}, y_{2}), (x_{1}, x_{4}, y_{4}), (x_{2}, x_{3}, y_{4}), (x_{2}, x_{4}, y_{1}), (x_{3}, x_{4}, y_{3}), \\ (y_{1}, y_{2}, z_{3}) & , (y_{1}, y_{3}, z_{2}), (y_{1}, y_{4}, z_{4}), (y_{2}, y_{3}, z_{4}), (y_{2}, y_{4}, z_{1}), (y_{3}, y_{4}, z_{3}), \\ (z_{1}, z_{2}, x_{3}) & , (z_{1}, z_{3}, x_{2}), (z_{1}, z_{4}, x_{4}), (z_{2}, z_{3}, x_{4}), (z_{2}, z_{4}, x_{1}), (z_{3}, z_{4}, x_{3}) \end{array}$
左上の対角成分から
$\begin{array}{r} (x_{1}, y_{1}, z_{1}), (x_{2}, y_{2}, z_{2}) \end{array}$
右下の対角成分から
$\begin{array}{r} (x_{3}, y_{1}, 13), (x_{4}, y_{2}, 13), (y_{3}, z_{1}, 13), (y_{4}, z_{2}, 13), (z_{3}, x_{1}, 13), (z_{4}, x_{2}, 13) \end{array}$
を得る. 数字に戻し, 列挙すると
$\begin{array}{rcl} S T S (13) = { & (1, 2, 7) & , (1, 3, 6), (1, 4, 8), (2, 3, 8), (2, 4, 5), (3, 4, 7), \\ (5, 6, 11) & , (5, 7, 10), (5, 8, 12), (6, 7, 12), (6, 8, 9), (7, 8, 11), \\ (3, 9, 10) & , (2, 9, 11), (4, 9, 12), (4, 10, 11), (1, 10, 12), (3, 11, 12), \\ (3, 5, 13) & , (4, 6, 13), (7, 9, 13), (8, 10, 13), (1, 11, 13), (2, 12, 13), \\ (1, 5, 9) & , (2, 6, 10)} \end{array}$
となる.

補遺. 簡単な $S T S (13)$ の構成法

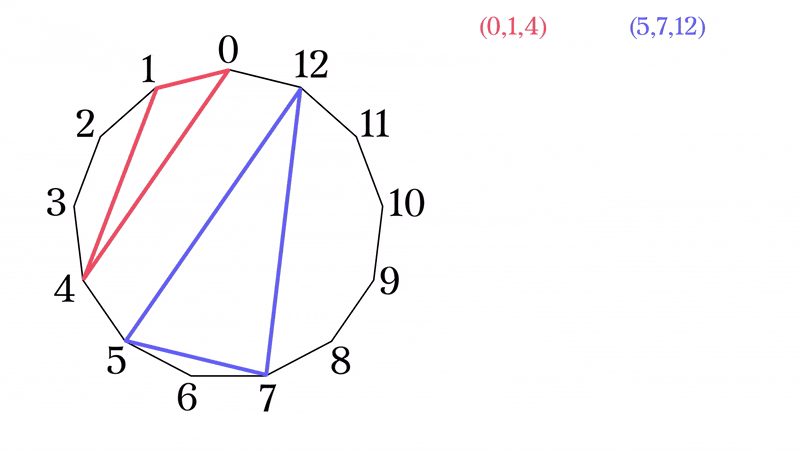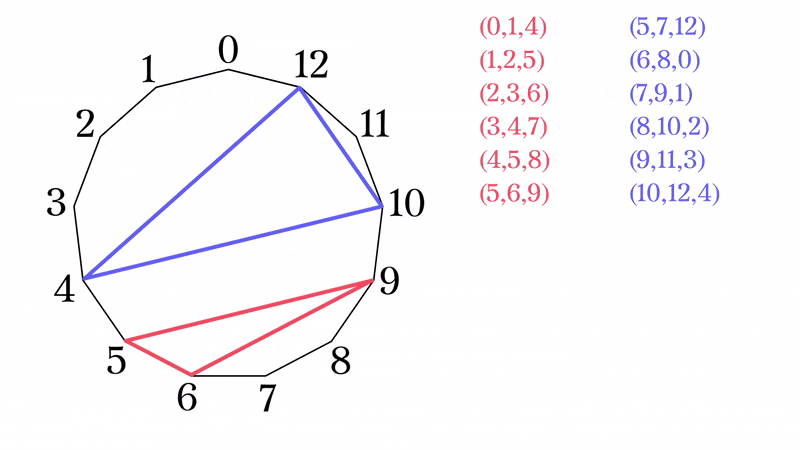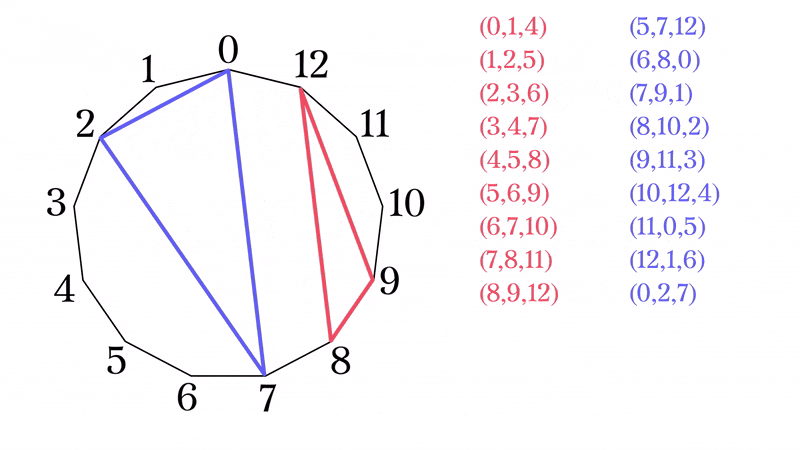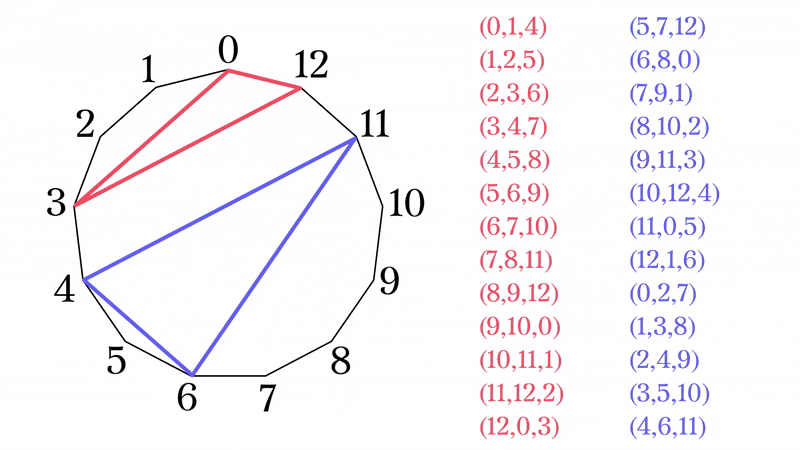
　一般のSTSの構成法が得られたわけだが, $S T S (13)$ の場合には, より簡素な構成法がある. $x \in Z / 13 Z$ として,
$\begin{array}{r} (x, x + 1, x + 4), (x, x + 2, x + 7) (m o d 13) \end{array}$
とブロックを構成すれば, $S T S (13)$ をなしている. 列挙すると
$\begin{array}{rcl} (0, 1, 4) & , (0, 2, 7), \\ (1, 2, 5) & , (1, 3, 8), \\ (2, 3, 6) & , (2, 4, 9), \\ (3, 4, 7) & , (3, 5, 10), \\ (4, 5, 8) & , (4, 6, 11), \\ (5, 6, 9) & , (5, 7, 12), \\ (6, 7, 10) & , (6, 8, 0), \\ (7, 8, 11) & , (7, 9, 1), \\ (8, 9, 12) & , (8, 10, 2), \\ (9, 10, 0) & , (9, 11, 3), \\ (10, 11, 1) & , (10, 12, 4), \\ (11, 12, 2) & , (11, 0, 5), \\ (12, 0, 3) & , (12, 1, 6) \end{array}$
これは13角形上の2種類の三角形を回転させることによって得られたブロックだと解釈できる.