トリプルシステムの直積
本筋から逸れる証明は折畳んでいる場合があるが, クリックで開くことができる.
STSの直積でSTSを構成する
STSにおいて, 点集合の2元を選べば一意にそれを含むブロックが決定されることから, $(\alpha_i,\alpha_j)$が含まれるブロックを$(\alpha_i,\alpha_j,\alpha_{i\circ j})$と表記する.
$\Omega_2$の元を固定した組$((\alpha_i,\beta_r),(\alpha_j,\beta_r))$については, ブロック$((\alpha_i,\beta_r),(\alpha_j,\beta_r),(\alpha_{i\circ j},\beta_r))$が一意に定まる.
これは$\Omega_1$の元を固定した組$((\alpha_i,\beta_r),(\alpha_i,\beta_s))$に関しても同様である.
上記のどの場合でもない組$((\alpha_i,\beta_r),(\alpha_i,\beta_r))\hspace{2mm}(i\neq j,r\neq s)$についてはブロック$((\alpha_i,\beta_r),(\alpha_i,\beta_r),(\alpha_{i\circ j},\beta_{r\circ s}))$が一意に定まる.
${\rm STS}(v_1v_2)$の形に対しては ラテン方格を用いた方法 よりも簡潔に構成できる. 以下では, ${\rm STS}(3)$を単なる3つ組と見做す.
例1. ${\rm STS}(9)$
${\rm STS}(9)$はアフィン平面として既に構成したが, STSの直積と捉えると, その本質が垣間見える.
$\Omega_1=\lbrace1,2,3\rbrace,\Omega_2=\lbrace4,5,6\rbrace$として$\Omega_1\times\Omega_2$の元を
\begin{eqnarray}
(1,6)\eqqcolon7,(2,6)\eqqcolon6,(3,6)\eqqcolon8,\\
(1,5)\eqqcolon5,(2,5)\eqqcolon4,(3,5)\eqqcolon3,\\
(1,4)\eqqcolon9,(2,4)\eqqcolon2,(3,4)\eqqcolon1
\end{eqnarray}
とおくと,
\begin{eqnarray}
{\rm STS}(9)=\lbrace(1,2,9),(3,4,5),(8,6,7),\\
(1,3,8),(2,4,6),(9,5,7),\\
(1,4,7),(2,5,8),(3,6,9),\\
(1,6,5),(3,2,7),(8,4,9)\rbrace
\end{eqnarray}
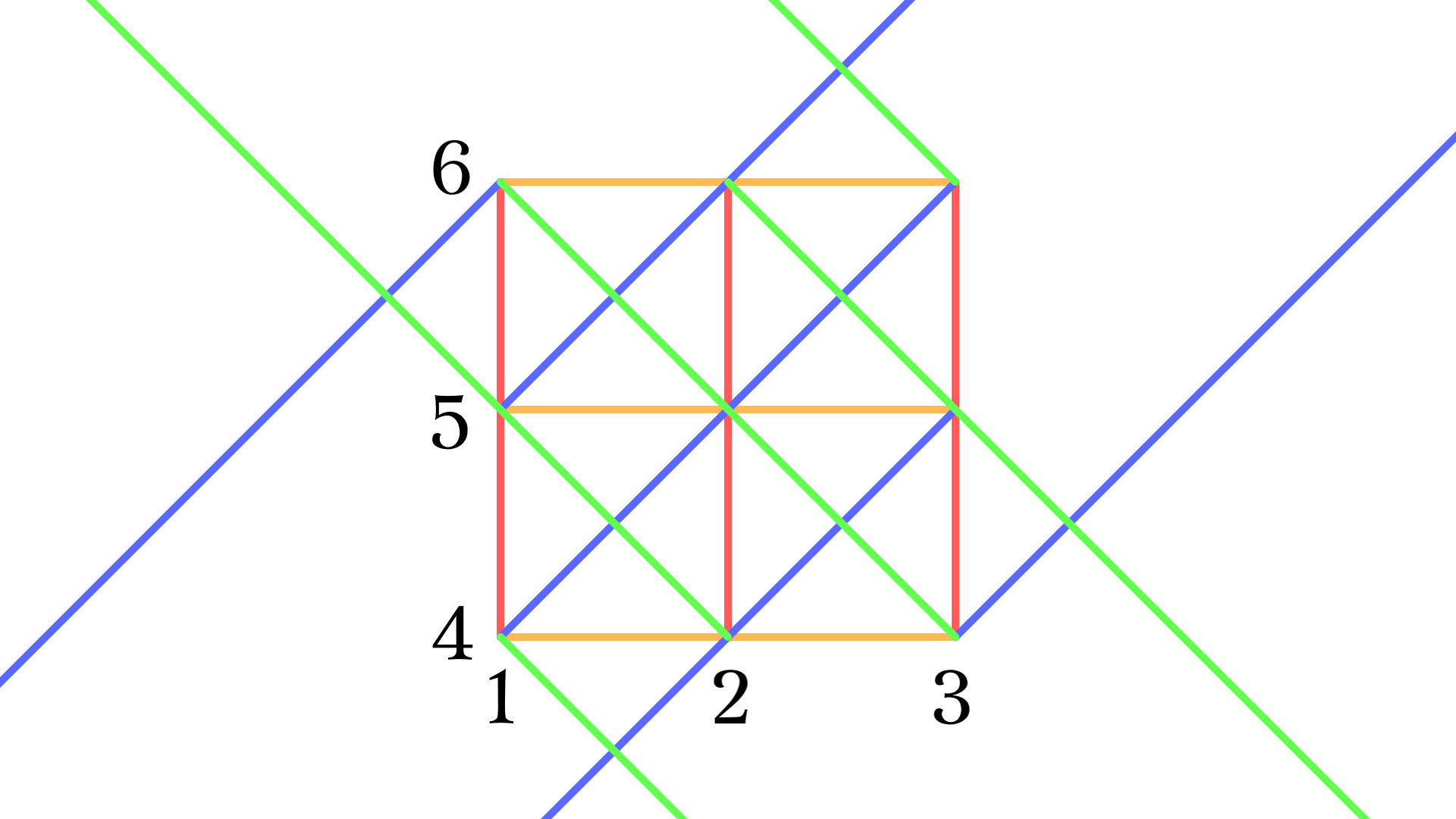平行類で彩色
平行類は平面$\mathbb{Z}/3\mathbb{Z}\times\mathbb{Z}/3\mathbb{Z}$の上で平行な直線の組だと理解できる.
例2. ${\rm STS}(117)$
${\rm STS}(9)$と${\rm STS}(13)$の直積として${\rm STS}(117)$を構成する.
${\rm STS}(9)$と${\rm STS}(13)$は以下のように構成できるのだった.
\begin{eqnarray}
{\rm STS}(9)&=&\left\{\begin{array}{ll}
(\overline{x-c},x,\overline{x+c}) & (c=1,2,4,x=1,4,7)\\
(\overline{1+c'},\overline{4+c'},\overline{7+c'}) & (c'=0,1,2)
\end{array}\right.\\\\
{\rm STS}(13)&=&\lbrace(x,\underline{x+1},\underline{x+4}),(x,\underline{x+2},\underline{x+7})|x\in\mathbb{Z}/13\mathbb{Z}\rbrace
\end{eqnarray}
ただし, $\overline{a}$は$a$を9で割った余り, $\underline{a}$は$a$を13で割った余りとする.
$\Omega_1=\lbrace1,2,\cdots,9\rbrace,\Omega_2=\lbrace1,2,\cdots,13\rbrace$に対して$\Omega_1\times\Omega_2$の元を
\begin{eqnarray}
(\alpha,\beta)\eqqcolon\alpha+9(\beta-1)\hspace{3mm}(\alpha\in\Omega_1,\beta\in\Omega_2)
\end{eqnarray}
と定める. このとき,
\begin{eqnarray}
{\rm STS}(117)=&\left\{\begin{array}{ll}
(\overline{\alpha-c}+9(\beta-1),\\
\alpha+9(\beta-1),\overline{\alpha+c}+9(\beta-1)) & (c=1,2,4)\\
(1+9(\beta-1)+c',\\
4+9(\beta-1)+c',7+9(\beta-1)+c') & (c'=0,1,2)\\
(\alpha+9\beta,\alpha+9\underline{(\beta+1)},\alpha+9\underline{(\beta+4)}) & (\alpha\in\Omega_1,\beta\in\Omega_2)\\
(\alpha+9\beta,\alpha+9\underline{(\beta+2)},\alpha+9\underline{(\beta+7)}) & (\alpha\in\Omega_1,\beta\in\Omega_2)\\
\end{array}\right.\end{eqnarray}
と構成できる. ただし, $\overline{0}=9,\underline{0}=13$とする.
ブロックの個数は$\dfrac{117\cdot116}{6}=2262$と, ここですべてを列挙することはできないが, $\alpha,\beta$に値を代入するだけでブロックが得られる.
