12次マシュー群2/3 - S(3,4,10)
- フィッシャー不等式
- 算術三角形
- 自己同型群
- アフィン平面
-
シュタイナー三重系
- マシュー群 $M_{11}$と$M_{12}$
- $S(2,3,9)$の性質
- $S(3,4,10)$の構成
- $M_{11}$と$M_{12}$
- 射影平面
- シュタイナー四重系
本筋から逸れる証明は折畳んでいる場合があるが, クリックで開くことができる.
$W_{10}$を$S(2,3,9)$の一点拡大として構成する. 始めに$W_{10}$の構成を示してから, それが機能していること, また拡大は一意であることを見る.
$S(2,3,9)$の拡大
$W_{10}$の縮小が$S(2,3,9)$なのだから, 自明なブロックとして$S(2,3,9)$に新たな点を加えた
\begin{eqnarray}
(1,2,9,10),(3,4,5,10),(6,7,8,10),\\
(1,3,8,10),(2,4,6,10),(5,7,9,10),\\
(1,4,7,10),(2,5,8,10),(3,6,9,10),\\
(1,5,6,10),(2,3,7,10),(4,8,9,10)
\end{eqnarray}
を持つ.
$S(2,3,9)$の平行類を
\begin{eqnarray}
A=\lbrace(1,2,9),(3,4,5),(6,7,8)\rbrace
\end{eqnarray}\begin{eqnarray}
B=\lbrace(1,3,8),(2,4,6),(5,7,9)\rbrace
\end{eqnarray}\begin{eqnarray}
C=\lbrace(1,4,7),(2,5,8),(3,6,9)\rbrace
\end{eqnarray}\begin{eqnarray}
D=\lbrace(1,5,6),(2,3,7),(4,8,9)\rbrace
\end{eqnarray}
とする.
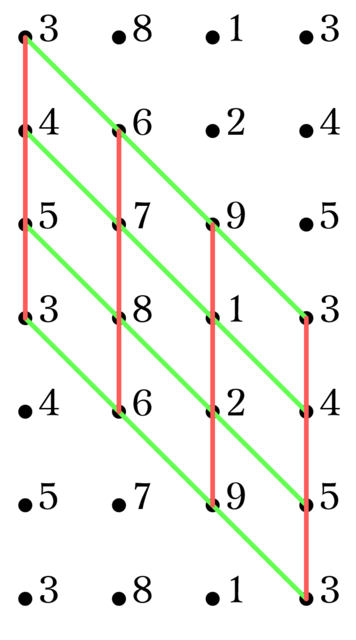
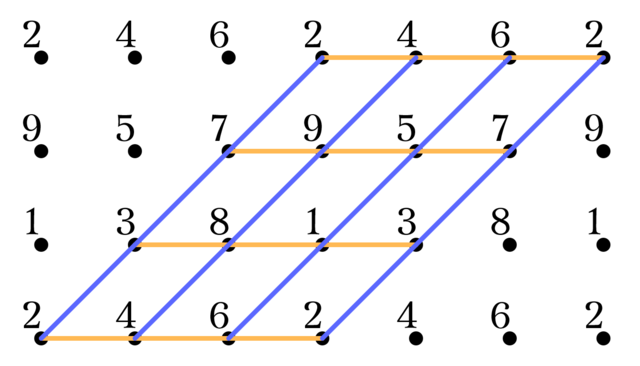
四角形は$\mqty(4\\2)=6$本の直線からなっており, それらの直線の平行類を見てみると必ず$A,A,B,C,C,D$や$A,B,C,C,D,D$のように, 2つの平行類から2本ずつ, 残り2つの平行類から1本ずつという構成になっている.
平行類が$A,A,B,C,C,D$の四角形を四角形ACのように表記する. Fig1. の通り, 四角形ACは9つあり, 上下左右へと9つの四角形を循環させれば, アフィン平面全体を覆い尽くせることが分かる. これは四角形BDも同様で, すぐに証明することだが四角形ACと四角形BDの計18ブロックは$W_{10}$の一部をなしている.
明示的に書き出してみると, 四角形ACから
\begin{eqnarray}
(1,3,4,9),(1,2,4,5),(2,3,5,9),\\
(1,6,7,9),(1,2,7,8),(2,6,8,9),\\
(3,4,6,7),(4,5,7,8),(3,5,6,8)
\end{eqnarray}
が, 四角形BDから
\begin{eqnarray}
(1,2,3,6),(1,3,5,7),(2,5,6,7),\\
(1,4,6,8),(1,5,8,9),(4,5,6,9),\\
(2,3,4,8),(3,7,8,9),(2,4,7,9)
\end{eqnarray}
が得られる. 先程のブロックと合わせて, 列挙すると
\begin{eqnarray}
\lbrace(1,2,9,10),(3,4,5,10),(6,7,8,10),\\
(1,3,8,10),(2,4,6,10),(5,7,9,10),\\
(1,4,7,10),(2,5,8,10),(3,6,9,10),\\
(1,5,6,10),(2,3,7,10),(4,8,9,10),\\
(1,3,4,9),(1,2,4,5),(2,3,5,9),\\
(1,6,7,9),(1,2,7,8),(2,6,8,9),\\
(3,4,6,7),(4,5,7,8),(3,5,6,8),\\
(1,2,3,6),(1,3,5,7),(2,5,6,7),\\
(1,4,6,8),(1,5,8,9),(4,5,6,9),\\
(2,3,4,8),(3,7,8,9),(2,4,7,9)\rbrace
\end{eqnarray}
となる.
AC | BDと分けたが, AB | CDまたはAD | BCのように分割しても同様に$W_{10}$が得られ, それらはすべて同型である.
証明
以後, 特定の状況や具体的な数字で証明を進めていくが, すべて一般性を崩さないことが容易に確認できる. また, $S(2,3,9)$では任意の2点を決めれば直線が一意に定まったことから, $\alpha_1,\alpha_2$が属する直線を$(\alpha_1,\alpha_2,\alpha_1\circ\alpha_2)$または$(\alpha_1,\alpha_2,\alpha_{1\circ2})$と表記する.
証明
任意の$u,v\in{{\mathbb{F}}_3}^2\backslash\lbrace0\rbrace,u\neq v$に対して, 基底$\lbrace u,u'\rbrace,\lbrace v,v'\rbrace$が取れ, 変換行列は正則で一意的であったから, ${\rm GL}_2(\mathbb{F}_3)$は${{\mathbb{F}}_3}^2\backslash\lbrace0\rbrace$に対して推移的に作用する.
このことから, ${{\mathbb{F}}_3}^2$のゼロでないベクトル$a_2-a_1,b_2-b_1$に対して, $A(a_2-a_1)=b_2-b_1$を満たす$A\in{\rm GL}_2(\mathbb{F}_3)$が存在し, ${\rm AGL}_2(\mathbb{F}_3)$の元
\begin{eqnarray}
g:{{\mathbb{F}}_3}^2&\longrightarrow&{{\mathbb{F}}_3}^2\\
u&\longmapsto&Au+b_1-Aa_1
\end{eqnarray}
は
\begin{eqnarray}
ga_1&=&Aa_1+b_1-Aa_1\\
&=&b_1\\
ga_2&=&Aa_2+b_1-Aa_1\\
&=&A(a_2-a_1)+b_1\\
&=&b_2-b_1+b_1\\
&=&b_2
\end{eqnarray}
を満足する.
$S(2,3,9)$の三角形は$\mqty(3\\2)=3$本の直線からなり, それらはすべて異なる平行類に含まれる. なぜなら, 三角形を構成する3本の直線のうち2本が同じ平行類に含まれているとすると,
異なる平行類に含まれる2本の直線の共通部分はちょうど1
であったから, 3本の直線の共通部分は多くても2にしかならず矛盾するためである.
${\rm AGL}_2(\mathbb{F}_3)$は直線の平行な関係を保存するため
, 三角形を三角形に, 四角形を四角形に移す.
証明
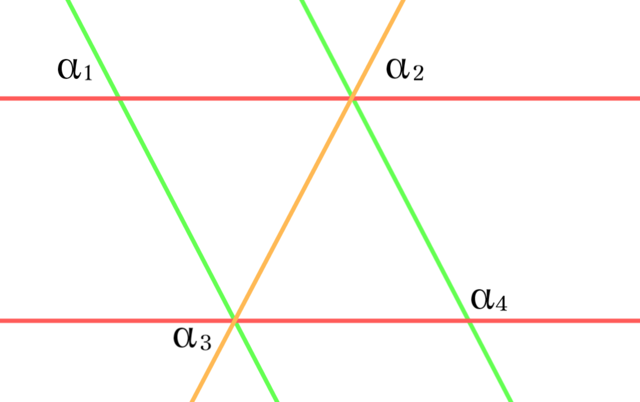
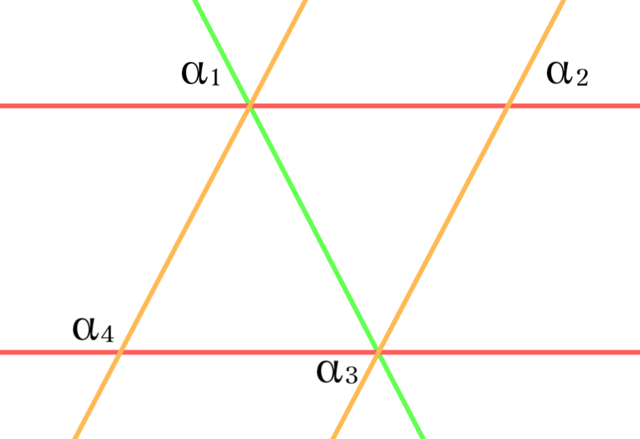
2点$\alpha_1,\alpha_2$に$\alpha_{1\circ2}$ではない$\alpha_3$を追加すれば三角形$\lbrace\alpha_1,\alpha_2,\alpha_3\rbrace$が得られる. 三角形に含まれる3本の直線はすべて異なる平行類に属しており,
\begin{eqnarray}
(\alpha_1,\alpha_2,\alpha_{1\circ2})\in A\\
(\alpha_2,\alpha_3,\alpha_{2\circ3})\in B\\
(\alpha_1,\alpha_3,\alpha_{1\circ3})\in C
\end{eqnarray}
とする.
次に, $\alpha_{1\circ2},\alpha_{2\circ3},\alpha_{3\circ1}$のいずれでもない$\alpha_4$を追加し, 四角形$\lbrace\alpha_1,\alpha_2,\alpha_3,\alpha_4\rbrace$について考える.
三角形$\lbrace\alpha_2,\alpha_3,\alpha_4\rbrace$をなす直線の平行類は$A,B,D$か$B,C,D$か$A,B,C$である.
[i] $A,B,C$であれば, すでに四角形のなかに$A,C$が2つずつ含まれている.
このとき, 平行な直線同士は交点を持たないため, $(\alpha_3,\alpha_4,\alpha_{3\circ4})\in A,(\alpha_2,\alpha_4,\alpha_{2\circ4})\in C$でなければならない. いま, $\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_{1\circ2},\alpha_{1\circ3},\alpha_{2\circ3},\alpha_{2\circ4},\alpha_{3\circ4}$の9点はすべて異なるため, $\alpha_{1\circ4}=\alpha_{2\circ3}$である. よって, $(\alpha_1,\alpha_4,\alpha_{1\circ4})$と$(\alpha_2,\alpha_3,\alpha_{2\circ3})$は異なる平行類に属していて, $(\alpha_1,\alpha_4,\alpha_{1\circ4})\in D$が確定する.
[ii] $A,B,D$と$B,C,D$は議論が対称であるから, $A,B,D$を仮定する.
$(\alpha_1,\alpha_4,\alpha_{1\circ4})$は$A,C,D$の直線と交わっているため, $B$に属する. このとき, 四角形$\lbrace\alpha_1,\alpha_2,\alpha_3,\alpha_4\rbrace$の平行類の構成は$A,A,B,B,C,D$となっていて, 条件を満たしている.
平行類を$A,B,C,D$としたとき, 四角形ABと四角形CDの集合を$Z_1$, 四角形ACと四角形BDの集合を$Z_2$, 四角形ADと四角形BCの集合を$Z_3$と定めると,
\begin{eqnarray} |Z_1|=|Z_2|=|Z_3|=18 \end{eqnarray}
${\rm AGL}_2(\mathbb{F}_3)$は$S(2,3,9)$の四角形を四角形に移し, 平行類に$\mathfrak{S}_4$として作用することから, $\mqty(4\\2)=6$つの型に四角形は同数ずつ含まれている. $S(2,3,9)$の
四角形の個数
は
\begin{eqnarray}
\frac{1}{24}3^2(3^2-1)(3^4-6\cdot3^2+5\cdot3-24)=54
\end{eqnarray}
であったからそれぞれの型に$\dfrac{54}{6}=9$個の四角形が含まれている.
よって, $i=1,2,3$に対して$|Z_i|=18$
(1) 6つの三角形
(2) 9つの四角形
に含まれる.
2点に対して残り1点を選ぶが, 同一直線上にあってはならないため, 6つの点の中から1点を取ればよい. よって, 2点は6つの三角形に含まれる.
(2)
2点を$\alpha_1,\alpha_2$とする. 避けなければいけない場合は
[i] $\alpha_1$と, $\alpha_2$でない他2点が同一直線上にある
[ii] $\alpha_2$と, $\alpha_1$でない他2点が同一直線上にある
まず, $\alpha_1,\alpha_2$とその直線上の点以外の6点から2点を選ぶ方法は$\mqty(6\\2)=15$通りで, そこから[i], [ii]を引く. ここで, [i], [ii]は独立であり, 対称性から同数のパターンがある.
[i] $\alpha_1$を通る直線は4本あり, そのうち1本は$\alpha_2$を含むものであるから他3本を避けなければいけない.
よって, $\alpha_1,\alpha_2$は$15-3-3=9$つの四角形に含まれる.
逆に, 任意の三角形が含まれる四角形が一意に定まるとき, 四角形の集合は$Z_i$のみである.
証明
($S(2,3,9)$の三角形は$Z_i$の四角形に一度だけ含まれること)
四角形の集合として$Z_1$, すなわち四角形ABと四角形CDを取る.
ここで三角形$T$をなす3直線はすべて異なる平行類に属しており, $T$を構成する直線が含まれない平行類が存在して, それを$D$とする. $T$の3点に点$\pi$を加えることで四角形$Q\in Z_1$を作ることを考える. 四角形には6本の直線があったのだから, 3本の直線を加えなければならない. 上記とほとんど同様の理由で加える3本の直線はすべて異なる平行類に属している. これらのことから, $Q$をなす6本の直線のうち$D$に属するものは必ず1本であるため, この四角形はAD, BD, CDではない. いま, 四角形の集合として$Z_1$を取ってきたのだから$Q$は四角形ABである.
さらに, $T$に対してこの$Q$が一意に定まることを示す.
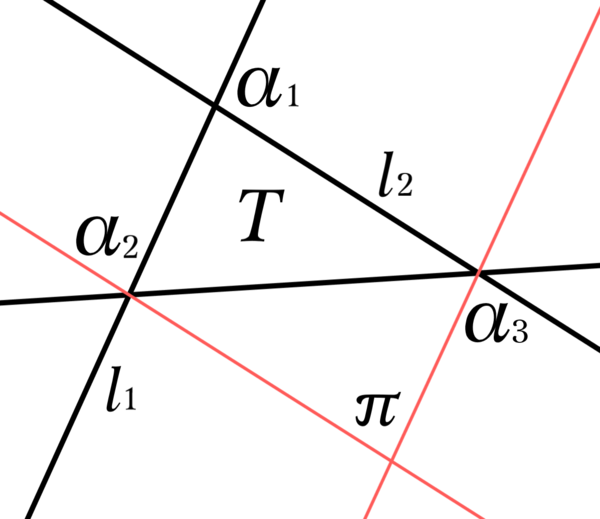
$T$の頂点を$\alpha_1,\alpha_2,\alpha_3$として, $T$の直線は$A,B,C$に含まれているのだから, $\alpha_1,\alpha_2$を通る直線を$l_1\in A$, $\alpha_1,\alpha_3$を通る直線を$l_2\in B$とできる.
アフィン平面の同値な条件
から$l_1$と共通部分を持たず$\alpha_3$を通る直線が一意に定まり, それを$l_1'\in A$とする. 同様に$l_2$と共通部分を持たず$\alpha_2$を通る直線が一意に定まり, それを$l_2'\in B$とする. このとき, $l_1'$と$l_2'$は異なる平行類に属するためちょうど1点で交わり, それを$\pi$とすれば, あとは$\alpha_1$と$\pi$を含む直線が一意に定まるため, 四角形を構成する直線がすべて一意に決定した.
始めに$T$を構成する直線が含まれない平行類を$D$としたが, これを$C$としても一意に四角形ABが定まり, $A,B$の場合は四角形CDとなる.
よって, 任意の三角形は$Z_1$の四角形に一意に含まれることが示された.
(三角形が含まれる四角形が一意に定まるとき, 四角形の集合は$Z_i$のみであること)
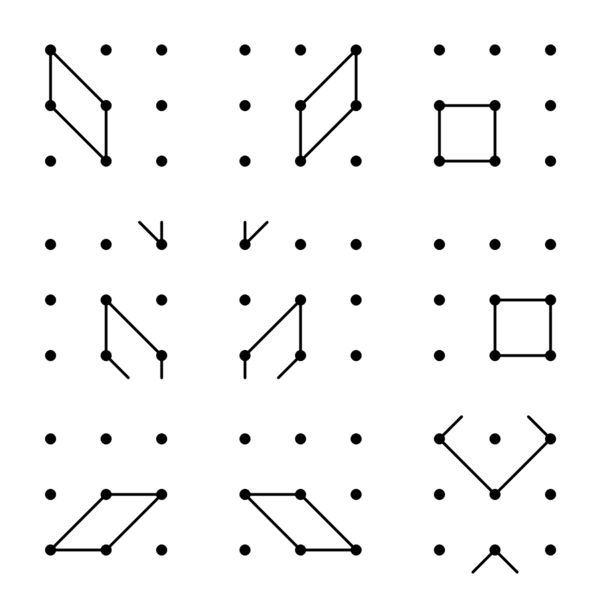
$S(2,3,9)$と$W_{10}$のブロックの数はそれぞれ$\dfrac{9\cdot8}{3\cdot2}=12,\dfrac{10\cdot9\cdot8}{4\cdot3\cdot2}=30$で, $W_{10}$の縮小が$S(2,3,9)$であったから, $W_{10}$は$30-12=18$個の四角形を含んでいる. ある2点$\alpha_1,\alpha_2$を含む9つの四角形の集合を$Q(\alpha_1,\alpha_2)$と表記し, すべての三角形が必ずひとつの四角形に含まれていると仮定する. このとき, $Q(\alpha_1,\alpha_2)$のそれぞれの四角形は$\alpha_1,\alpha_2$を頂点に持つ三角形をちょうど2つ含んでいて, $\alpha_1,\alpha_2$を含む三角形は6つであったから, $Q(\alpha_1,\alpha_2)$から$\alpha_1,\alpha_2$以外に共通部分がないように$\dfrac{6}{2}=3$つ四角形を選べば, $\alpha_1,\alpha_2$を頂点に持つ三角形を網羅できる.
$S(2,3,9)$を${\mathbb{F}_3}^2$と同一視
し, $(a,b)\in{\mathbb{F}_3}^2$を単に$ab$と書く. $\mathbb{F}_3=\lbrace0,1,2\rbrace$として, $Q(11,12)$を列挙すると
\begin{eqnarray}
\Theta_1=\mathcal{P}\cup\lbrace00,02\rbrace\hspace{5mm}\Theta_2=\mathcal{P}\cup\lbrace20,22\rbrace\hspace{5mm}\Theta_3=\mathcal{P}\cup\lbrace21,22\rbrace\\
\Theta_4=\mathcal{P}\cup\lbrace20,21\rbrace\hspace{5mm}\Theta_5=\mathcal{P}\cup\lbrace00,01\rbrace\hspace{5mm}\Theta_6=\mathcal{P}\cup\lbrace01,02\rbrace\\
\Theta_7=\mathcal{P}\cup\lbrace01,22\rbrace\hspace{5mm}\Theta_8=\mathcal{P}\cup\lbrace02,21\rbrace\hspace{5mm}\Theta_9=\mathcal{P}\cup\lbrace00,20\rbrace
\end{eqnarray}

ただし, $\mathcal{P}=\lbrace11,12\rbrace$.
$11,12$以外に共通部分がないような3つの四角形の集合は
\begin{eqnarray}
\mathfrak{Q}_1&=&\lbrace\Theta_1,\Theta_4,\Theta_7\rbrace\\
\mathfrak{Q}_2&=&\lbrace\Theta_2,\Theta_5,\Theta_8\rbrace\\
\mathfrak{Q}_3&=&\lbrace\Theta_3,\Theta_6,\Theta_9\rbrace\\
\mathfrak{Q}_4&=&\lbrace\Theta_7,\Theta_8,\Theta_9\rbrace
\end{eqnarray}
ですべてである. このとき, $\mathfrak{Q}_1,\mathfrak{Q}_2,\mathfrak{Q}_3\in Z_i$であり, $\mathfrak{Q}_4\notin Z_i$を取ったときに矛盾が生じることを確認する.
ここで, $Q(01,11)$を考える. すべての四角形を列挙すると,
\begin{eqnarray}
\varUpsilon_1=\mathcal{Q}\cup\lbrace10,20\rbrace\hspace{5mm}\varUpsilon_2=\mathcal{Q}\cup\lbrace12,22\rbrace\hspace{5mm}\varUpsilon_3=\mathcal{Q}\cup\lbrace00,10\rbrace\\
\varUpsilon_4=\mathcal{Q}\cup\lbrace02,22\rbrace\hspace{5mm}\varUpsilon_5=\mathcal{Q}\cup\lbrace00,20\rbrace\hspace{5mm}\varUpsilon_6=\mathcal{Q}\cup\lbrace02,12\rbrace\\
\varUpsilon_7=\mathcal{Q}\cup\lbrace00,12\rbrace\hspace{5mm}\varUpsilon_8=\mathcal{Q}\cup\lbrace02,10\rbrace\hspace{5mm}\varUpsilon_9=\mathcal{Q}\cup\lbrace20,22\rbrace
\end{eqnarray}
$\mathcal{Q}=\lbrace01,11\rbrace$であり, $01,11$以外に共通部分がないような3つの四角形の集合は
\begin{eqnarray}
\mathfrak{R}_1&=&\lbrace\varUpsilon_1,\varUpsilon_4,\varUpsilon_7\rbrace\\
\mathfrak{R}_2&=&\lbrace\varUpsilon_2,\varUpsilon_5,\varUpsilon_8\rbrace\\
\mathfrak{R}_3&=&\lbrace\varUpsilon_3,\varUpsilon_6,\varUpsilon_9\rbrace\\
\mathfrak{R}_4&=&\lbrace\varUpsilon_7,\varUpsilon_8,\varUpsilon_9\rbrace
\end{eqnarray}
ここで$\varUpsilon_2=\Theta_7,\varUpsilon_6=\Theta_6,\varUpsilon_7=\Theta_5$であるから$\mathfrak{Q}_4=\lbrace\Theta_7=\varUpsilon_2,\Theta_8,\Theta_9\rbrace$を取ったとすると, 四角形の集合として$\mathfrak{Q}_4\cup\mathfrak{R}_2$を取らなければいけないが,
\begin{eqnarray}
\mathfrak{Q}_4\cup\mathfrak{R}_2=\lbrace\Theta_7=\varUpsilon_2,\Theta_8,\Theta_9,\varUpsilon_5,\varUpsilon_8\rbrace
\end{eqnarray}
において, $\Theta_9\cap\varUpsilon_5=\lbrace00,11,20\rbrace$となり, すべての三角形がちょうど一つの四角形に含まれているという仮定に反する.
したがって, $\mathfrak{Q}_4$は取れず, 同様に$\mathfrak{R}_4$も仮定を満たすためには不適.
${\rm AGL}_2(\mathbb{F}_3)$は$S(2,3,9)$に対して
1. 二重推移的に作用したこと
2. 三角形と四角形に作用すること
3.
平行類に置換を引き起こすこと
を併せて考えれば, 仮定を満足させる四角形の集合は$Z_i$のみである.
$S(2,3,9)$には
\begin{eqnarray}
\frac{1}{6}3(3+1)(3^4-3^3-2\cdot3^2+2\cdot3-6)=72
\end{eqnarray}
個の三角形が含まれ
ていて, 一つの四角形は4つの三角形からなっていたから, $|Z_i|=18$個の四角形で$18\cdot4=72$個すべての三角形を網羅できている.
$S(2,3,9)$の一点拡大は$Z_1,Z_2,Z_3$のみで, ${\rm AGL}_2(\mathbb{F}_3)$はこれらに$\mathfrak{S}_3$として置換を引き起こす. このような${\rm AGL}_2(\mathbb{F}_3)$の元を同型とすればよい.
$W_{10}$のある点$\alpha$の縮小は$S(2,3,9)$と同型であり, これは 同型を除いて一意に定まった のだった. 定理5-系1から$\alpha$を含まないブロックも同型を除いて一意であり, したがって$W_{10}$は一意である.
