12次マシュー群3/3 - M11,12の性質, 四元数群との関係
- フィッシャー不等式
- 算術三角形
- 自己同型群
- アフィン平面
-
シュタイナー三重系
- マシュー群 $M_{11}$と$M_{12}$
- S(2,3,9)の性質
- S(3,4,10)の構成
- $M_{11}$と$M_{12}$
- 射影平面
- シュタイナー四重系
構成したシュタイナーシステム
(2,3,7)
,
(2,3,9)
,
(2,3,13)
,
(2,3,117)
(2,4,16)
,
(2,5,25)
(3,4,8)
,
(3,4,10)
(4,5,11)NEW
(5,6,12)NEW
本筋から逸れる証明は折畳んでいる場合があるが, クリックで開くことができる.
$S(2,3,9)$のクロス
$W_{10}=S(3,4,10)$のブロックは直線と2種類の四角形であった.
$W_{11,12}$では新たにクロスと呼ばれる点集合が加わるが, クロスは単に四角形の補集合と捉えることができる.
以下, $S\coloneqq S(2,3,9)$とする.
(1) $\Xi$と共通部分を持たず, 対角点$\delta$を共有する四角形$\Xi^*$が一意に存在する.
(2) $S\backslash\Xi$のある点を$\gamma$とする. $\Xi\cup\lbrace\gamma\rbrace$に含まれる四角形が$\Xi$のみであれば, $\gamma$は$\Xi$の対角点である.
証明
(1)
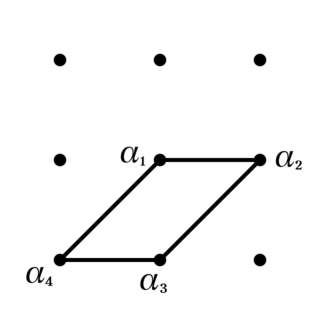
$\Xi\cup\lbrace\delta\rbrace$の外には4点しかないため, 条件を満たす四角形は存在するとすれば一意である. よって, $S\backslash(\Xi\cup\lbrace\delta\rbrace)$の点が共線上にないことを示せばよい.
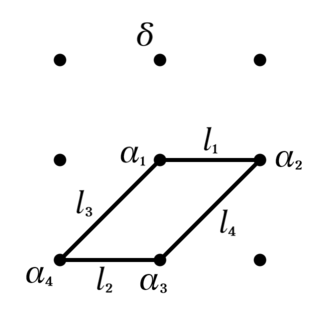
\begin{eqnarray}
\Xi&=&\lbrace\alpha_1,\alpha_2,\alpha_3,\alpha_4\rbrace\\
l_1&=&\lbrace\alpha_1,\alpha_2,\alpha_{1\circ2}\rbrace\in A\\
l_2&=&\lbrace\alpha_3,\alpha_4,\alpha_{3\circ4}\rbrace\in A\\
l_3&=&\lbrace\alpha_1,\alpha_4,\alpha_{1\circ4}\rbrace\in B\\
l_4&=&\lbrace\alpha_2,\alpha_3,\alpha_{2\circ3}\rbrace\in B\\
Q&\coloneqq&S\backslash(\Xi\cup\lbrace\delta\rbrace)\\
&=&\lbrace\alpha_{1\circ2},\alpha_{3\circ4},\alpha_{1\circ4},\alpha_{2\circ3}\rbrace
\end{eqnarray}
とおいて, $Q$の中の3点が直線$l$上にあるとすると, 同じ平行類の直線は交点を持たないことから$l\notin A,B$.
$l=\lbrace\alpha_{1\circ2},\alpha_{3\circ4},\alpha_{1\circ4}\rbrace\in C$とすると, $l\in C$と$l_4\in B$は交点を持たないが, これは異なる平行類の直線が1点で交じることと矛盾する. 他の場合でも, $l\in C,D$とすると同種の矛盾が生じる. したがって, $Q$のどの3点も共線上にはない.
(2)
(1)と同じ状況を考え,
\begin{eqnarray}
l_5&=&\lbrace\alpha_1,\alpha_3,\delta\rbrace\in C\\
l_6&=&\lbrace\alpha_2,\alpha_4,\delta\rbrace\in D
\end{eqnarray}
とする.
$\gamma=\alpha_{1\circ2}$とおくと, 四角形$\lbrace\alpha_1,\alpha_{1\circ2},\alpha_3,\alpha_4\rbrace$が$\Xi\cup\lbrace\gamma\rbrace$に含まれ, 条件に適合しない. $\gamma=\alpha_{3\circ4},\alpha_{1\circ4},\alpha_{2\circ3}$も同様に不適.
$\gamma=\delta$としよう. $\Xi\cup\lbrace\delta\rbrace$から$\alpha_1$または$\alpha_3$を除いた場合は直線$l_6$が, $\alpha_2$または$\alpha_4$を除いた場合は直線$l_5$が$\Xi\cup\lbrace\gamma\rbrace$に含まれるため, $\Xi\cup\lbrace\gamma\rbrace$の中の四角形は$\Xi$のみである.
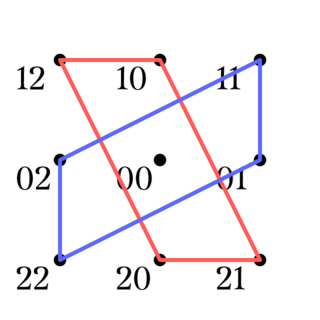
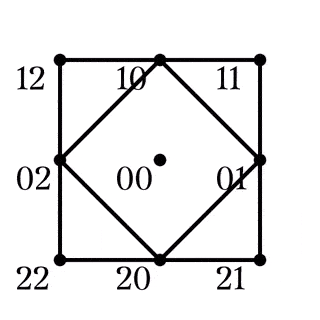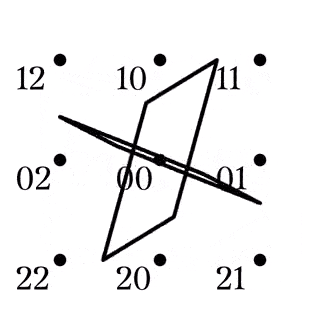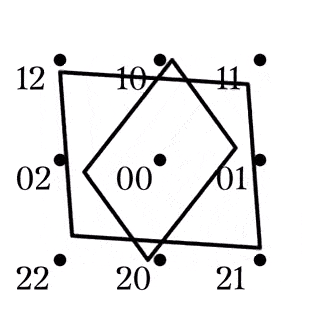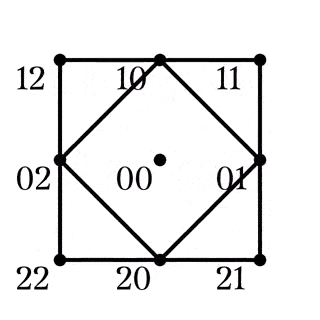
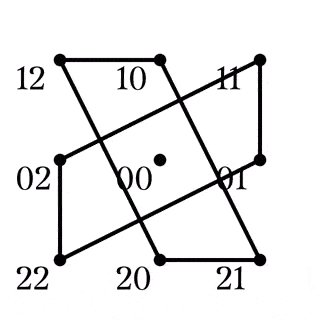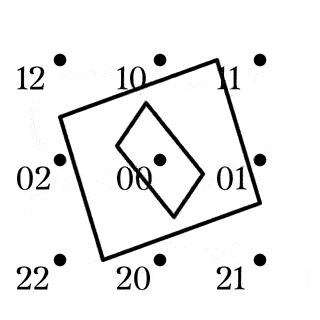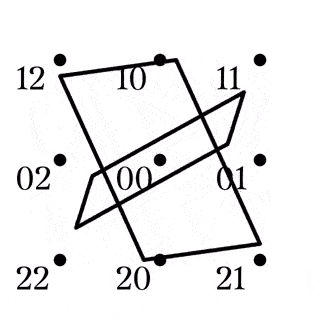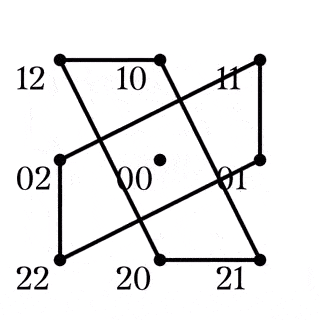
(1)は, 任意の四角形の補集合は四角形とその対角点に一意に分解できるとも読み替えられる (Fig2). また, 異なる平行類に属する2本の直線はある四角形とその対角点でもある (Fig3).
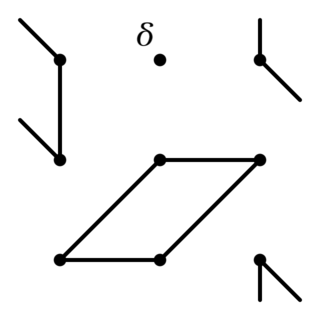

四角形とその対角点の和集合をクロスと呼ぶ.
また, 四角形の対角線が属する2つの平行類を$X,Y$としたとき, $XY$をクロスの型と言い, クロスXYなどと表記する.
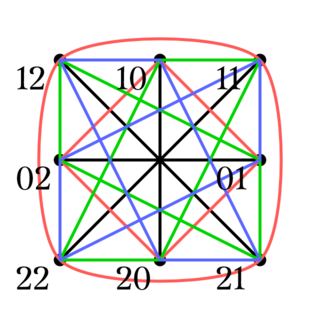
四角形の型を定めたとき
と同様に, $S$の平行類を$A,B,C,D$として, クロスABとクロスCDの集合を$C_1$, クロスACとクロスBDの集合を$C_2$, クロスADとクロスBCの集合を$C_3$とする.
$W_{11}$の構成
$W_{11}$は$S$の2点拡大として得られ, 追加された点を$\alpha,\beta$とすると$W_{11}$のブロックは以下のように構成される.
| ブロック | 個数 |
|---|---|
| $\lbrace\alpha,\beta\rbrace$と直線 | $12$ |
| $\lbrace\alpha\rbrace$と四角形$Z_1$ | $18$ |
| $\lbrace\beta\rbrace$と四角形$Z_2$ | $18$ |
| クロス$C_3$ | $18$ |
| $66$ |
証明
\begin{eqnarray}\begin{array}{ll} B_1:\lbrace\alpha,\beta\rbrace\cup\Lambda & (\Lambda\in\mathcal{B})\\ B_2:\lbrace\alpha\rbrace\cup\Xi & (\Xi\in Z_i)\\ B_3:\lbrace\beta\rbrace\cup\Xi & (\Xi\in Z_j)\\ B_4:C_k & (i,j,k=1,2,3,\hspace{2mm}i\neq j\neq k) \end{array}\end{eqnarray}
としたとき, $(\Omega\cup\lbrace\alpha,\beta\rbrace,\bigcup_{l=1}^{4}B_l)$は$S(4,5,11)$をなす.
証明
\begin{eqnarray}
\sum_{l=1}^{4}|B_l|&=&66\\
&=&\frac{11\cdot10\cdot9\cdot8}{5\cdot4\cdot3\cdot2}\\
&=&|S(4,5,11)|
\end{eqnarray}
よりすべての4つ組が$B_l\hspace{2mm}(l=1,2,3,4)$のいずれかに少なくとも1回含まれているのなら, ちょうど1回含まれていることになる.
[i] $(\alpha,x_1,x_2,x_3)\hspace{2mm}(x_1,x_2,x_3\in\Omega)$について, $x_3=x_{1\circ2}$のとき, $(\alpha,\beta,x_1,x_2,x_{1\circ2})\in B_1$.
$x_3\neq x_{1\circ2}$のとき,
三角形$(x_1,x_2,x_3)$は$Z_i$の四角形に一度だけ含まれる
ことから, ${}^{\exists!}x_4\in\Omega,(\alpha,x_1,x_2,x_3,x_4)\in B_2$.
$(\beta,x_1,x_2,x_3),(\alpha,\beta,x_1,x_2)$についても同様.
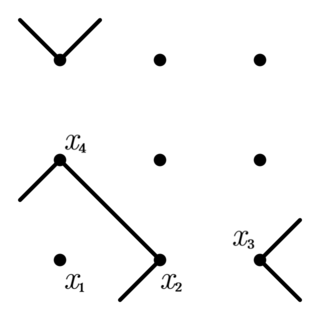
[ii] $U=(x_1,x_2,x_3,x_4)$について, どの3点も共線上にない, 即ち$U$が四角形をなすとき, $U$が$Z_i$に含まれる型なら$(\alpha,U)\in B_2$, $Z_j$に含まれる型なら$(\beta,U)\in B_3$, $Z_k$に含まれる型なら$(\delta_U,U)\in B_4$. ただし, $\delta_U$は$U$の対角点で, $(\alpha,U)=(\alpha,x_1,x_2,x_3,x_4)$と略記している. $Z_i,Z_j,Z_k$で四角形の6つの型を網羅できていて, なおかつこれらのブロックは一意に定まる.
$U$が四角形をなさない, つまり3点が共線上にあるとき, $x_3=x_{1\circ2}$としても一般性は崩れない. また, この場合$U$に2直線以上が含まれないことはほとんど明らか.
直線$(x_1,x_2,x_{1\circ2}),(x_1,x_4,x_{1\circ4})$が含まれる平行類をそれぞれ$X,Y$, $C_k$をクロスXYとクロスX'Y'の集合とすると, 4点$\Xi=(x_2,x_4,x_{1\circ2},x_{1\circ4})$はどの3点も共線上になく, $\Xi\cup\lbrace x_1\rbrace$を含む四角形は$\Xi$のみであるから, $x_1$は$\Xi$の対角点である. よって, $(x_1,x_2,x_3,x_4,x_{1\circ4})\in B_4$であり, 以上の議論は選んだ4点にかかわらず一意に進む.
$W_{11}$の2点$\alpha,\beta$を固定すると, $W_{11}$のブロックは
- $\lbrace\alpha,\beta\rbrace$と$S$の直線
- $\alpha$と四角形の集合$Z_i$
- $\beta$と四角形の集合$Z_j\hspace{2mm}(i,j=1,2,3,i\neq j)$
で構成される. $\alpha,\beta$を含まないブロックは$S$の点のみからなっていて,
任意の5点は少なくとも1つの四角形を含む
ため, $W_{11}$の5つ組は$Z_k\hspace{2mm}(k=1,2,3,k\neq i,j)$の四角形を含まなければならない. このとき, $Z_k$の四角形に各々の対角点以外の点を付け加えると, $Z_i,Z_j$の四角形を含んでしまうため, 5つ組はクロス$C_k$である.
対角点が四角形に対して一意に定まったこと, $W_{10}$は同型を除いて一意であることを考えれば, 任意の$W_{11}$に対して上記の議論が成り立ち, 同型をつくることができる.
$M_{11}$の鋭四重推移性と単純性
$W_{11}$の自己同型群は$M_{11}$と表記され, 次のよく知られた性質を証明する.
- 位数は$11\cdot10\cdot9\cdot8=7920$
- $W_{11}$に対して鋭四重推移的に作用する
- 単純群である
そのための準備として, 多重推移群と単純群についての定理を示しておく. 作用に関する用語をいくつか導入することになるが, 先回りしてFig4. に包含関係を整理しておいた. 下で示すすべての定理を包括しているわけではないことに注意.
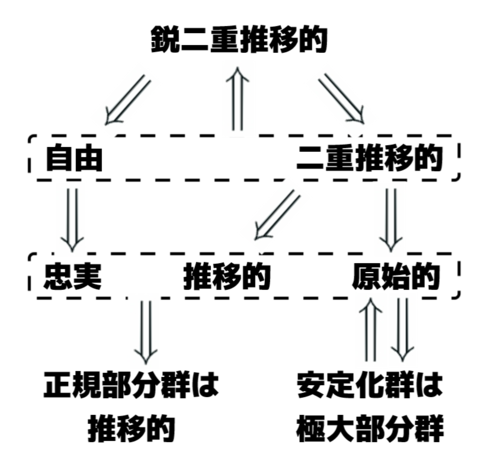
- 鋭二重推移的と, 自由かつ二重推移的は同値
- 自由ならば忠実
- 二重推移的なら推移的
- 二重推移的なら原始的
- 原始的と, 任意の点の安定化群が極大部分群であることは同値
- 推移的かつ忠実原始的ならば, 非自明な正規部分群は推移的
多重推移群に関する補題
以下, $\Omega$の長さ$n$の順序組を$\Omega^{(n)}$と表し, $n$-組と呼ぶ. また, $G$が$\Omega$に作用していて, $g\in G,(x_1,\cdots,x_k),(y_1,\cdots,y_k)\in\Omega^{(k)},g(x_1,\cdots,x_k)=(y_1,\cdots,y_k)$であることを
\begin{xy}\xymatrix{
(x_1,\cdots,x_k) \ar[d]_{g}\\
(y_1,\cdots,y_k)
}\end{xy}
と表記する. これはケイリーグラフ$(\Omega^{(k)},G)$であるが, 導入の目的は議論の整理であって, この図式に厳密性は要求しない.
群$G$が$\Omega$に作用しているとする.
任意の$x\in X$に対して$gx=x$を満たす$g\in G$が単位元のみであるとき, 作用が忠実であるという.
ある$x\in X$に対して$gx=x$を満たす$g\in G$が単位元のみであるとき, 作用が自由であるという.
任意の$g\in G$に対して, $gB\cap B=B$または$\varnothing$なる$B\subseteq\Omega$がすべて1点集合か$\Omega$であるとき, 作用が原始的であるという. 条件を満たす$B$が存在しないときも原始的であるとする.
定義から自由な作用は明らかに忠実であるが, 逆は成り立たない.
\begin{xy}\xymatrix{
(x_1,\cdots,x_{k-1}) \ar[d]^{g} & (x_1,\cdots,x_{k}) \ar[d]^{{}^{\exists}g\in G}\\
(y_1,\cdots,y_{k-1}) & (y_1,\cdots,y_{k})
}\end{xy}
$(x_1,\cdots,x_{k-1}),(y_1,\cdots,y_{k-1})\in\Omega^{(k-1)}$に対して, $x_k\in\Omega\backslash\lbrace x_1,\cdots,x_{k-1}\rbrace,y_k\in\Omega\backslash\lbrace y_1,\cdots,y_{k-1}\rbrace$を取ると, $G$は$k$重推移であるから
\begin{eqnarray}
g(x_1,\cdots,x_{k})=(y_1,\cdots,y_{k})
\end{eqnarray}
を満たす$g\in G$が存在する. よって,
\begin{eqnarray}
g(x_1,\cdots,x_{k-1})=(y_1,\cdots,y_{k-1})
\end{eqnarray}
証明
\begin{xy}\xymatrix{
(x_1,\cdots,x_i) \ar[d]^{{}^{\exists}g\in G} & (x_{i+1},\cdots,x_k) \ar[d]^{g} & (x_1,\cdots,x_k) \ar[dd]^{{}^{\exists}f=hg}\\
(y_1,\cdots,y_i) \ar[d]^{h} & (z_{i+1},\cdots,z_k) \ar[d]^{{}^{\exists}h\in G_{(y_1,\cdots,y_i)}}\\
(y_1,\cdots,y_i) & (y_{i+1},\cdots,y_k) & (y_1,\cdots,y_k)
}\end{xy}
$(x_1,\cdots,x_k),(y_1,\cdots,y_k)\in\Omega^{(k)}$に対して,
\begin{eqnarray}
f(x_1,\cdots,x_k)=(y_1,\cdots,y_k)
\end{eqnarray}
なる$f\in G$の存在を示したい.
$G$は$i$重推移であったから,
\begin{eqnarray}
g(x_1,\cdots,x_i)=(y_1,\cdots,y_i)
\end{eqnarray}
を満たす$g\in G$が存在して,
\begin{eqnarray}
g(x_{i+1},\cdots,x_k)=(z_{i+1},\cdots,z_k)
\end{eqnarray}
とする. ここで, $(y_1,\cdots,y_i)$の安定化群は$\Omega\backslash\lbrace y_1,\cdots,y_i\rbrace$に対して$k-i$重推移的であるから
\begin{eqnarray}
h(z_{i+1},\cdots,z_k)=(y_{i+1},\cdots,y_k)
\end{eqnarray}
を満足する$h\in G_{(y_1,\cdots,y_i)}$が存在する.
以上のことから,
\begin{eqnarray}
(hg)(x_1,\cdots,x_i,x_{i+1},\cdots,x_k)&=&h(y_1,\cdots,y_i,z_{i+1},\cdots,z_k)\\
&=&(y_1,\cdots,y_i,y_{i+1},\cdots,y_k)
\end{eqnarray}
$f=hg$とすればよい.
証明
[i] 群$G$が$\Omega$へ鋭$k$重推移的に作用する, 即ち
\begin{eqnarray}
{}^{\forall}(x_1,\cdots,x_k),(y_1,\cdots,y_k)\in\Omega^{(k)},\\
{}^{\exists!}g\in G,g(x_1,\cdots,x_k)=(y_1,\cdots,y_k)
\end{eqnarray}
であると仮定する.
\begin{xy}\xymatrix{
(x_1,\cdots,x_k) \ar[d]^{h} \ar@{.>}[rd]^{{}^{\exists!}g\in G}\\
(x_1,\cdots,x_k) \ar[r]_{{}^{\exists}g\in G} & (y_1,\cdots,y_k)
}\end{xy}
このとき, $G$は明らかに$k$重推移で, $h(x_1,\cdots,x_k)=(x_1,\cdots,x_k)$を満たす$h\in G$を取ると,
\begin{eqnarray}
(gh)(x_1,\cdots,x_k)=(y_1,\cdots,y_k)
\end{eqnarray}
一意性から$gh=g$. したがって, $h=1$で安定化群は単位群に限られる.
[ii] $G$が$k$重推移的かつ$\Omega$の$k$-組へ自由に作用すると仮定する.
\begin{xy}\xymatrix{
(x_1,\cdots,x_k) \ar[d]^{{}^{\exists}g\in G} \ar[rd]^{1}\\
(y_1,\cdots,y_k) \ar[r]_{{}^{\exists}h^{-1}\in G} & (x_1,\cdots,x_k)
}\end{xy}
$g,h\in G,(x_1,\cdots,x_k),(y_1,\cdots,y_k)\in\Omega^{(k)}$が
\begin{eqnarray}
g(x_1,\cdots,x_k)&=&(y_1,\cdots,y_k)\\
h(x_1,\cdots,x_k)&=&(y_1,\cdots,y_k)
\end{eqnarray}
を満たすとすると,
\begin{eqnarray}
(h^{-1}g)(x_1,\cdots,x_k)=(x_1,\cdots,x_k)
\end{eqnarray}
安定化群は単位群に限られるとしたため, $h^{-1}g=1$.
したがって, $g=h$から$G$は鋭$k$重推移である.
定理4から$G$は$k$重推移である. よって, 定理5より$G$が$\Omega$の$k$-組へ自由に作用することを示せばよい.
\begin{eqnarray}
g(x_1,\cdots,x_k)=(x_1,\cdots,x_k)
\end{eqnarray}
とすると, $(x_1,\cdots,x_k)$は順序組であるから
\begin{eqnarray}
g(x_1,\cdots,x_i)=(x_1,\cdots,x_i)
\end{eqnarray}
より, $g$は$i$-組$(x_1,\cdots,x_i)$の安定化群に含まれる.
$G_{(x_1,\cdots,x_i)}$は$\Omega\backslash\lbrace x_1,\cdots,x_i\rbrace$へ鋭$k-i$重推移的に作用するのだから,
\begin{eqnarray}
g(x_{i+1},\cdots,x_k)=(x_{i+1},\cdots,x_k)
\end{eqnarray}
を満たす$g$は単位元に限られる.
これは次の図式が成り立つことを示している.
\begin{xy}\xymatrix{
(x_1,\cdots,x_i) \ar[d]^{{}^{\exists}g\in G} & (x_{i+1},\cdots,x_k) \ar[d]^{g} & (x_1,\cdots,x_k) \ar@{.>}[dd]^{{}^{\exists!}f=hg}\\
(y_1,\cdots,y_i) \ar[d]^{h} & (z_{i+1},\cdots,z_k) \ar@{.>}[d]^{{}^{\exists!}h\in G_{(y_1,\cdots,y_i)}}\\
(y_1,\cdots,y_i) & (y_{i+1},\cdots,y_k) & (y_1,\cdots,y_k)
}\end{xy}
\begin{eqnarray} \#G=n(n-1)\cdots(n-k+1)\#G_{(x_1,\cdots,x_k)} \end{eqnarray}
ただし, $|\Omega|=n,(x_1,\cdots,x_k)\in\Omega^{(k)}$.
補題3を繰り返し適用して, $G$は$\Omega$へ推移的に作用していると分かる. よって,
\begin{eqnarray}
\#G=|Gx_1|\#G_{x_1}=n\#G_{x_1}
\end{eqnarray}
同様に$G$は二重推移的に$\Omega$に作用しているから
\begin{eqnarray}
\#G=|G_{x_1}x_2|\#G_{(x_1,x_2)}=(n-1)\#G_{(x_1,x_2)}
\end{eqnarray}
帰納的に
\begin{eqnarray}
\#G=n(n-1)\cdots(n-k+1)\#G_{(x_1,\cdots,x_k)}
\end{eqnarray}
が成り立つ.
\begin{eqnarray} \#G=n(n-1)\cdots(n-k+1) \end{eqnarray}
ただし, $|\Omega|=n$.
定理5から明らか.
証明
任意の$\beta,\gamma\in\Omega\cup\lbrace\alpha\rbrace\eqqcolon\Omega^*$に対して, $\psi\beta=\gamma$なる$\psi\in{\rm Aut}T^*$が存在することを示す.
$T$は同型を除いて一意なのだから, $T^*$の縮小${T^*}_\beta,{T^*}_\gamma$の間に
\begin{eqnarray}
B\in{T^*}_\beta\iff\phi B\in{T^*}_\gamma
\end{eqnarray}
を満足する全単射$\phi:\Omega^*\backslash\lbrace\beta\rbrace\longrightarrow\Omega^*\backslash\lbrace\gamma\rbrace$が存在する.
そこで次の写像を考える.
\begin{eqnarray}
\psi:\Omega^*&\longrightarrow&\Omega^*\\
\Omega^*\backslash\lbrace\beta\rbrace\ni x&\longmapsto&\phi x\\
\beta&\longmapsto&\gamma
\end{eqnarray}
この$\psi$が$T^*$の自己同型になっていることを確認する.
$\beta$を含む$T^*$のブロック$(\beta,B_1)$について
\begin{eqnarray}
(\beta,B_1)\in T^*&\iff&B_1\in{T^*}_\beta\\
&\iff&\phi B_1\in{T^*}_\gamma\\
&\iff&(\gamma,\phi B_1)\in T^*\\
&\iff&\psi(\beta,B_1)\in T^*
\end{eqnarray}
$\Omega\backslash\lbrace\beta\rbrace$の$t+1$元$x_1,\cdots,x_{t+1}$が含まれる唯一のブロックを$B_2$, $B_2$の残りの点を$x_{t+2},\cdots,x_{k+1}$とする.
このとき,
\begin{eqnarray}
\phi B_2=\lbrace\phi x_1,\cdots,\phi x_t,\phi x_{t+1},\cdots,\phi x_{k+1}\rbrace
\end{eqnarray}
で, これは$\phi x_1,\cdots,\phi x_{t}$が含まれる唯一のブロックである.
したがって, $\psi B_2=\phi B_2\in T^*$から$\psi\in{\rm Aut}T^*$.
単純群に関する補題
群の多重推移性と単純性は密接に関係している. $5$次以上の交代群が単純群であることの証明は種々知られているが, そのひとつに$6$次以上の$n$次交代群が$n$点集合に$n-2$重推移的に作用することと$A_5$の単純性から帰納的に$A_n$の単純性を示す方法がある. 本題の$M_{11,12}$についても同様の指針を取り, $M_{11}$の単純性を別箇で示した後, $M_{12}$の単純性を証明する.
任意の$g\in G,x\in\Omega$に対して, $gHx\cap Hx\neq\varnothing$を定立すれば, 作用が推移的であるから
\begin{eqnarray}
gHx\cap Hx=Hgx\cap Hx=Hx
\end{eqnarray}
よって, $gHx\cap Hx=Hx$または$\varnothing$.
作用が原始的であるから$Hx=\lbrace x\rbrace,\Omega$が成り立ち, 前者を仮定して矛盾を導く.
$Hx=\lbrace x\rbrace$より$H\leq G_x$.
$H$の正規性から
\begin{eqnarray}
H=gHg^{-1}\leq gG_xg^{-1}={}^{g}G_x=G_{gx}
\end{eqnarray}
これは任意の$g\in G$について成り立ち, 作用が推移的であるから, $H$はすべての$\Omega$の点の安定化群の部分群である. 即ち,
\begin{array}{lll}
& {}^\forall x\in X, & H\leq G_x\\
\iff & {}^\forall x\in X, & H\leq\lbrace g\in G|gx=x\rbrace\\
\iff && H\leq\lbrace g\in G|{}^\forall x\in X,gx=x\rbrace\\
\iff && H\leq1
\end{array}
であるが, これは$H$の非自明性に反する.
以上から, $Hx=\Omega$であり, $H$は$\Omega$へ推移的に作用する.
証明
$H\cap G_x\triangleleft G_x$で, $G_x$の単純性から
\begin{eqnarray}
H\cap G_x=1,G_x
\end{eqnarray}
$H\cap G_x=1$のとき, 定理9から$H$は$\Omega$に対して推移的であり, かつ安定化群が単位群に限られるため, 定理5から$H$は鋭推移的.
$H\cap G_x=G_x$のとき, $G_x$が$G$の極大部分群であることを示せたとすると
\begin{eqnarray}
G_x=H\lor H=G
\end{eqnarray}
だが, $H$の推移性から前者はあり得ないため, $H=G$から$G$は単純である.
よって, $G_x$が$G$の極大部分群であることを示せばよい.
$G_x\lneq K\lneq G$なる部分群$K$の存在を仮定すると, $gKx\cap Kx\neq\varnothing$のとき,
\begin{eqnarray}
{}^\exists k,k'\in K, gk'x&=&kx\\
k^{-1}gk'x&=&x\\
k^{-1}gk'&\in&G_x\lneq K\\
g&\in&kKk'^{-1}=K
\end{eqnarray}
ゆえに$gKx=Kx$から, ${}^\forall g\in G,gKx\cap Kx=Kx$または$\varnothing$.
作用が原始的であるから, $Kx=\lbrace x\rbrace,\Omega$.
前者は$Kx\leq G_x$を成り立たせるが, これは$G_x\lneq K$に反するためあり得ない.
後者を仮定すると,
\begin{xy}\xymatrix@C=45pt{
x \ar[d]_{{}^\exists k\in K} \ar[rd]^{gk\in G_x\leq K}\\
y \ar[r]_{{}^\exists g\in G\backslash K}& x
}\end{xy}
$K$が推移的であるから$x,y\in\Omega$に対して, $kx=y$なる$k\in K$が取れる.
また, $G$も推移的であるから$gy=x$なる$g\in G\backslash K$を取れるはずだが,
\begin{eqnarray}
gkx&=&x\\
gk&\in&G_x\leq K\\
g&\in&Kk^{-1}=K
\end{eqnarray}
となり矛盾する.
したがって, このような$K$は存在せず, $G_x$は極大部分群である.
証明の途中で
作用が原始的$\Longrightarrow$任意の点の安定化群が極大部分群である
を示したが, 実は逆も成り立つ.
ただし逆は以降で使わないため, 証明は付さない.
群$G$が$\Omega$に二重推移的に作用しているとする.
$\Omega$の部分集合$B$と$x,y\in B,z\in\Omega\backslash B$を取ると, $gx=x\land gy=z$なる$g\in G$が存在するため, $gB\cap B\neq B,\varnothing$.
群$G$が$X,Y$に作用しているとする. 任意の$x\in X,g\in G$に対して, $f(gx)=gf(x)$を満たす写像$f:X\rightarrow Y$を$G$-写像, $f$が全単射であれば$G$-同型であるといい, $X\cong Y$と表記する.
\begin{eqnarray}
f:H^\#&\longrightarrow&\Omega\backslash\lbrace x\rbrace\\
h&\longmapsto&hx
\end{eqnarray}
と定める. $h,h'\in H^\#$に対して
\begin{eqnarray}
f(h)&=&f(h')\\
hx&=&h'x\\
h^{-1}h'x&=&x\\
\end{eqnarray}
$H$の鋭推移性から$h^{-1}h'=1\iff h=h'$.
よって$f$は単射で, 全射であることは$H$の鋭推移性から明らか.
加えて, $g\in G_x,h\in H^\#$に対して
\begin{eqnarray}
f({}^gh)&=&f(ghg^{-1})\\
&=&ghg^{-1}x\\
&=&ghx\hspace{8mm}(\because g^{-1}\in G_x)\\
&=&gf(h)
\end{eqnarray}
より$H^\#\cong\Omega\backslash\lbrace x\rbrace$.
$G$は$\Omega$に対して$k$重推移的.
$\Longrightarrow x\in \Omega,G_x$は$\Omega\backslash\lbrace x\rbrace$に対して$k-1$重推移的.
$\Longrightarrow G_x$は$H^\#\coloneqq H\backslash\lbrace1\rbrace$に対して$k-1$重推移的. (定理12から直ちに従う)
$\Longrightarrow h\in H^\#,(G_x)_h$は$H^\#\backslash\lbrace h\rbrace$に対して$k-2\geq2$.
$\Longrightarrow (G_x)_h$は$H^\#\backslash\lbrace h\rbrace$に対して二重推移的. (補題3を繰り返し適用)
$\Longrightarrow (G_x)_h$は$H^\#\backslash\lbrace h\rbrace$に対して原始的. (補題11)
このことから, $g\in(G_x)_h,gB\cap B=B$を満たす$B=\lbrace h',hh'\rbrace\subset\Omega$が存在して,
\begin{eqnarray}
H^\#\backslash\lbrace h\rbrace&=&\lbrace h',hh'\rbrace\\
H&=&\lbrace1,h,h',hh'\rbrace\\
&\cong& C_2\times C_2
\end{eqnarray}
定理10から, $G$の非自明な正規部分群$H$が$\Omega$へ鋭推移的に作用するか, $G$が単純であるかのいずれかが成り立つ.
上の定理から前者が成り立つとすると, $k=4$だがこれは矛盾.
したがって, $G$は単純である.
$n$次交代群$A_n$は$n-2$重推移性を持ち, 細々としたことを除けば$A_5,A_6$の単純性と上の系から$7$次以上の交代群は単純であると分かる.
$M_{11}$と四元数群$Q_8$
$M_{11}$の鋭四重推移性は, 3つ組$(y_1,y_2,y_3)\in{W_{11}}^{(3)}$の安定化群$H\coloneqq(M_{11})_{(y_1,y_2,y_3)}$が$W_{11}\backslash\lbrace y_1,y_2,y_3\rbrace$に対して鋭推移的に作用することを起点に, 定理6を繰り返し適用して示される. そのため, $H$の$W_{11}\backslash\lbrace y_1,y_2,y_3\rbrace\cong{\mathbb{F}_3}^2\backslash\lbrace00\rbrace$への作用に関して直感的な説明を与えた後で, 本題の証明をする.
$H$の構造決定
まず,
$W_{11}$の2点縮小$S(2,3,9)$が${\mathbb{F}_3}^2$と同一視できた
ことから, $W_{11}$の3点縮小は, ${\mathbb{F}_3}^2\backslash\lbrace00\rbrace$と見ることができる. そして, その自己同型群はアフィン群${\rm AGL}_2(\mathbb{F}_3)$の原点を固定した一般線型群$L\coloneqq{\rm GL}_2(\mathbb{F}_3)$の部分群になっている. $L$についての詳細は鈴木(上)suzp.69-80を参照.
$W_{11}$のブロックを
\begin{eqnarray}\begin{array}{ll}
B_1:\lbrace y_1,y_2\rbrace\cup\Lambda & (\Lambda\in\mathcal{B})\\
B_2:\lbrace y_1\rbrace\cup\Xi & (\Xi\in Z_1)\\
B_3:\lbrace y_2\rbrace\cup\Xi & (\Xi\in Z_2)\\
B_4:C_3
\end{array}\end{eqnarray}
と表すと, $H$は$B_i\hspace{2mm}(i=1,2,3,4)$のブロックを$B_i$へ移すことから, 四角形の集合$Z_j\hspace{2mm}(j=1,2,3)$を同じく$Z_j$に移す. 即ち, 平行類の分割$AB|CD,AC|BD,AD|BC$を保存するような${\rm GL}_2(\mathbb{F}_3)$の部分群が$H$であり, 作用
\begin{eqnarray}
L\times\lbrace Z_i\rbrace_{i=1,2,3}&\longrightarrow&\lbrace Z_i\rbrace_{i=1,2,3}\\
(g,Z_i)&\longmapsto&gZ_i=\lbrace g\Xi|\Xi\in Z_i\rbrace
\end{eqnarray}
のもとで
\begin{eqnarray}
\#H&=&\#(L_{Z_1})_{Z_2}\\
&=&\frac{\#L}{|L\cdot Z_1||L_{Z_1}\cdot Z_2|}\\
&=&\frac{48}{3\cdot2}\\
&=&8
\end{eqnarray}
と位数が求められる.
$L$を置換として見て, 以上の条件を満たすような元を調べると
\begin{eqnarray}
R_B=\mqty(01&10&02&20)\mqty(11&12&22&21)\\
R_C=\mqty(01&12&02&21)\mqty(10&11&20&22)\\
R_D=\mqty(01&11&02&22)\mqty(10&21&20&12)
\end{eqnarray}
が見つかる. 非可換で, 二面体群と同型でないことが簡単な計算から分かるため
\begin{array}{ll}
H & =\lbrace1,R_B,R_C,R_D,\\
& {R_B}^2={R_C}^2={R_D}^2,\\
& {R_B}^{-1},{R_C}^{-1},{R_D}^{-1}\rbrace\\
& \cong Q_8
\end{array}
が決定され, これは$L$の正規部分群である.
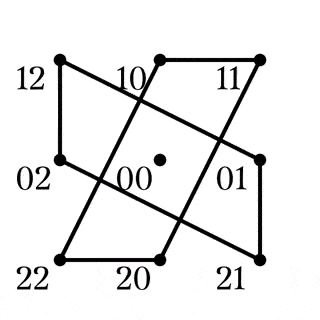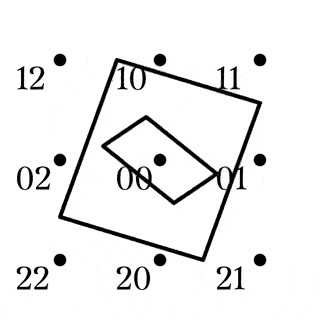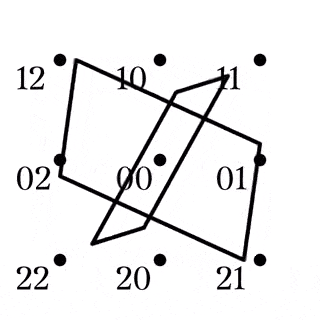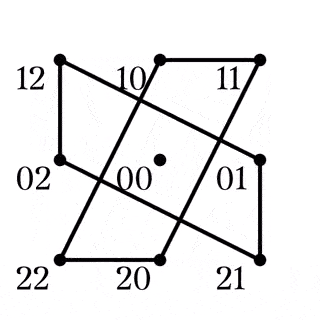
$H$の鋭推移性


四角形$AB|CD\in Z_1$
四角形$AC|BD\in Z_2$
四角形$AD|BC\in Z_3$
$R_B,R_C,R_C$から${\mathbb{F}_3}^2\backslash\lbrace00\rbrace$への作用で, 点の軌道を追うと, Fig.6-8のようになる. ${\mathbb{F}_3}^2\backslash\lbrace00\rbrace$と$8$次完全グラフ$K_8$を同一視したとき, これらは$K_8$の2-因子(連結されている部分がすべて2-正則)になっていて, ${R_B}^2$の軌道と和を取ればFig9. のように$K_8$の1-因子と2-因子による分解が得られる.
による1-因子
赤い辺は$R_B$の軌道, 緑の辺は$R_C$, 青い辺は$R_D$の軌道であり, ${R_B}^2$の軌道は黒い辺で描かれている. Fig9. は$K_8$として, 辺に過不足がないことが簡単に確認でき, $Q_8$は${\mathbb{F}_3}^2\backslash\lbrace00\rbrace$に対して鋭推移的である.
$H$とアフィン平面
逆に$Q_8$の性質から$H$の条件を説明することも可能.
- Fig6:四角形ABと四角形CD$\in Z_1$
- Fig7:四角形ACと四角形BD$\in Z_2$
- Fig8:四角形ADと四角形BC$\in Z_3$
であることが見て取れ, すべて対角点$00$を共有している. また, Fig10-15から, $R_B,R_C,R_D$は$Z_i\hspace{2mm}(i=1,2,3)$の四角形を$Z_i$へ移していることが見て取れる.

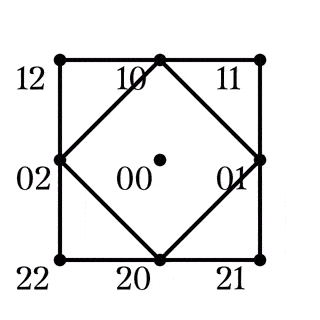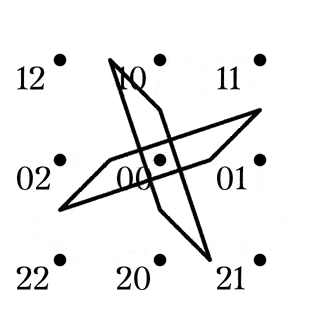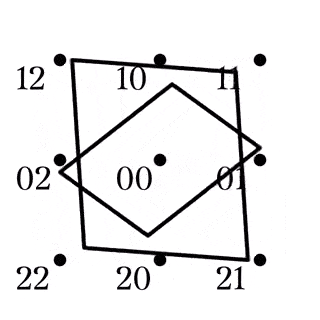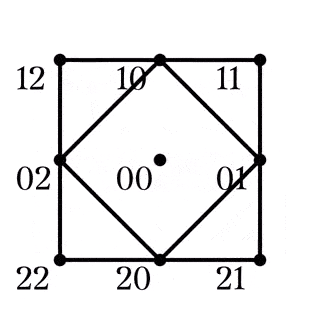
$AC|BD\in Z_2$への作用
$AB|CD\in Z_1$への作用
$AB|CD\in Z_1$への作用
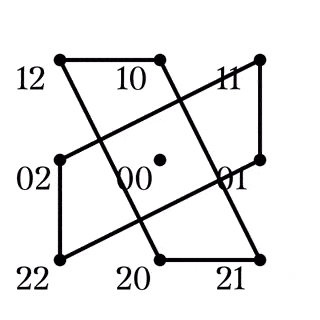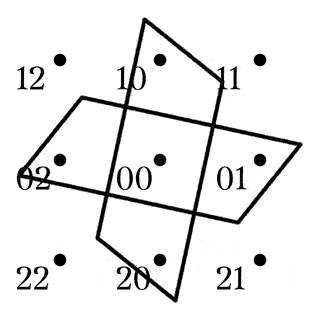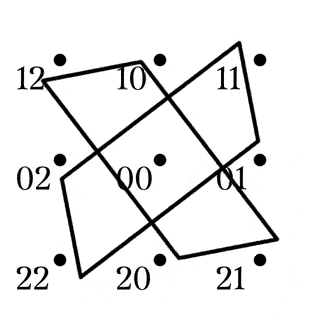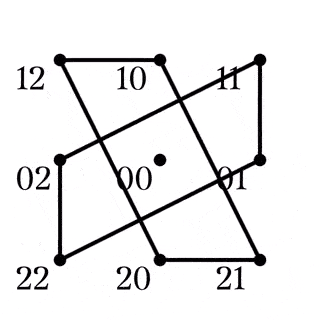
$AD|BC\in Z_3$への作用
$AD|BC\in Z_3$への作用
$AC|BD\in Z_2$への作用
証明
$y_1,y_2,y_3\in W_{11}$として, 次のことが示せたとする.
[i] $M_{11}$は$W_{11}$に対して推移的
[ii] $(M_{11})_{y_1}$は$W_{11}\backslash\lbrace y_1\rbrace$に対して推移的
[iii] $(M_{11})_{(y_1,y_2)}$は$W_{11}\backslash\lbrace y_1,y_2\rbrace$に対して推移的
[iv] $(M_{11})_{(y_1,y_2,y_3)}$は$W_{11}\backslash\lbrace y_1,y_2,y_3\rbrace$に対して鋭推移的
このとき, 図式
\begin{xy}\xymatrix@C=18pt{
x_1 \ar[d]|-{{}^{\exists}g_1\in M_{11}} & x_2 \ar[d]^{g_1} & (x_1,x_2) \ar[dd]^{{}^{\exists}g_3=g_2g_1} &&& (x_3,x_4) \ar[dd]^{g_3} & (x_1,x_2,x_3,x_4) \ar@{.>}[dddd]^{{}^{\exists!}g_7=g_6g_3}\\
y_1 \ar[d]_{g_2} & z_2 \ar[d]|-{{}^\exists g_2\in(M_{11})_{y_1}}\\
y_1 & y_2 & (y_1,y_2) \ar[dd]^{g_6} & z_3 \ar[d]|-{{}^\exists g_4\in(M_{11})_{(y_1,y_2)}} & z_4 \ar[d]^{g_4} & (z_3,z_4) \ar@{.>}[dd]^{{}^{\exists!}g_6=g_5g_4}\\
&&& y_3 \ar[d]_{g_5} & w_4 \ar@{.>}[d]|-{{}^{\exists!}g_5\in(M_{11})_{(y_1,y_2,y_3)}}\\
&& (y_1,y_2) & y_3 & y_4 & (y_3,y_4) & (y_1,y_2,y_3,y_4)
}\end{xy}
から$M_{11}$の鋭四重推移性が導け, 定理7-系から
\begin{eqnarray}
\#M_{11}=11\cdot10\cdot9\cdot8=7920
\end{eqnarray}
が得られる. よって, [i],[ii],[iii],[iv]を証明すればよい.
[i] $M_{11}$は$W_{11}$に対して推移的
定理8と
$W_{10}$の一意性
から直ちに従う.
[ii] $(M_{11})_{y_1}$は$W_{11}\backslash\lbrace y_1\rbrace$に対して推移的
縮小の自己同型群は安定化群と同型
であったことから
\begin{eqnarray}
(M_{11})_{y_1}&=&({\rm Aut}W_{11})_{y_1}\\
&\cong&{\rm Aut}(W_{11})_{y_1}\\
&\cong&{\rm Aut}W_{10}\\
&=&M_{10}\\
W_{11}\backslash\lbrace y_1\rbrace&\cong&W_{10}
\end{eqnarray}
定理8から$M_{10}$は$W_{10}$に推移的に作用する.
よって, $(M_{11})_{y_1}$は$W_{11}\backslash\lbrace y_1\rbrace$に対して推移的.
[iv] $(M_{11})_{(y_1,y_2,y_3)}$は$W_{11}\backslash\lbrace y_1,y_2,y_3\rbrace$に対して鋭推移的
上の話と重複する部分が多いため, 略述する.
[iii]は[iv]から従う.
証明
\begin{eqnarray}
\#M_{11}=11\cdot10\cdot9\cdot8=2^4\cdot3^2\cdot5\cdot11
\end{eqnarray}
$M_{11}$のシロー$11$群を$P$,
\begin{eqnarray}
m=[M_{11}:N_{M_{11}}(P)],r=[N_{M_{11}}(P):P]
\end{eqnarray}
とおくと,
\begin{eqnarray}
mr\#P&=&\#M_{11}\\
mr&=&720\\
mr&\equiv&5\hspace{2mm}({\rm mod}\hspace{1mm}11)\\
r&\equiv&5\hspace{2mm}({\rm mod}\hspace{1mm}11)
\end{eqnarray}
ここで,
・$M_{11}$は明らかに$11$次対称群の部分群
・$N_{\mathfrak{S}_{11}}(P)\cong C_{10}\rtimes C_{11}$
であることから
\begin{eqnarray}
11=\#P\leq\#N_{M_{11}}(P)&\leq&\#N_{\mathfrak{S}_{11}}(P)=11\cdot10\\
r&\leq&10
\end{eqnarray}
が成り立つため, $r=5,m=144$が確定する.
$M_{11}$の非自明な正規部分群を$H$とすると, 定理9から$H$は$W_{11}$に推移的に作用して,
\begin{eqnarray}
\#H\equiv0\hspace{2mm}({\rm mod}\hspace{1mm}11)
\end{eqnarray}
$H$の正規性とシローの定理から$M_{11}$のシロー$11$群はすべて$H$に含まれる.
よって
\begin{eqnarray}
\#H&=&[H:N_H(P)][N_H(P):P]\#P\\
&=&[H:N_{M_{11}}(P)][N_H(P):P]\cdot11\\
&=&1584[N_H(P):P]
\end{eqnarray}
$r'\coloneqq[N_H(P):P]$とすると, $1584r'$は$7920$を割り切るから,$r'=1,5$.
$r'=5$では$\#H=\#G$となり矛盾.
$r'=1$とする. $P$と共役な部分群の個数は$m=144$個で, 各々から単位元を除いて, $H$の中で位数$p$の元の個数は$144\cdot(11-1)=1440$.
$\#H=1584$であるから, 位数が$p$ではない元の個数は$1584-1440=144$個.
ここで, $W_{11}$の点$x$を固定するような$H$の元の個数は
\begin{eqnarray}
\#H_x&=&\frac{\#H}{|H\cdot x|}\\
&=&144
\end{eqnarray}
位数$p$の元が$x$を固定しないことを考えると, 位数が$p$ではない元はすべて$x$を固定する. これが任意の$W_{11}$の点について成り立ち, すべての$W_{11}$の点の安定化群が同一でなおかつ単位群であるということになるが, これは$m=144$に反する.
以上から, $M_{11}$は非自明な正規部分群を持たない.
$W_{12}$の構成
$W_{12}$を$W_{11}$の1点拡大として構成し, 同時に親和性の高いコンウェイのMiniMOGについても紹介する. また, ここでの詳述は避けるが, 他の代表的な構成法として,
を挙げておく.
$W_{11}$の1点拡大
$W_{12}$は$S$の3点拡大として得られ, 追加された点を$\alpha,\beta,\gamma$とすると$W_{12}$のブロックは以下のように構成される.
| ブロック | 個数 |
|---|---|
| $\lbrace\alpha,\beta,\gamma\rbrace$と直線 | $12$ |
| $\lbrace\beta,\gamma\rbrace$と四角形$Z_1$ | $18$ |
| $\lbrace\alpha,\gamma\rbrace$と四角形$Z_2$ | $18$ |
| $\lbrace\alpha,\beta\rbrace$と四角形$Z_3$ | $18$ |
| $\lbrace\alpha\rbrace$とクロス$C_1$ | $18$ |
| $\lbrace\beta\rbrace$とクロス$C_2$ | $18$ |
| $\lbrace\gamma\rbrace$とクロス$C_3$ | $18$ |
| 平行な2直線の組 | $12$ |
| $132$ |
コンウェイのMiniMOG
クリックして開く
次に, コンウェイによるMiniMOGまたはKittenと呼ばれる構成法を紹介する. これは, 12点集合の適当な5点から$W_{12}$の構造を持つように残り1点を選ぶ方法で, 後で見るように$W_{12}$は一意であるから上の構成と本性上の違いはない.
MiniMOGとKittenという呼称の所以を少し. MOGとは, カーティスによる$W_{24}=S(5,8,24)$の構成法, ミラクル・オクタッド・ジェネレーター (Miracle Octad Generator)の略称であり, このMOGの手法をコンウェイとカーティスが$W_{12}$に流用したことからMiniMOGと呼ばれている. Kittenの方に関して確証はないが, ジュディス・カーによる絵本『Mog the Forgetful Cat』(
わすれんぼうのねこ モグ (Amazon)
)からMOGを猫と見立て, その小型版のMiniMOGをKitten(子猫)と呼んでいると思われる.
まず12点集合の9点を$3\times3$に並べる.
\begin{array}{ccc}
2&4&6\\
9&5&7\\
1&3&8
\end{array}
これまでの記事と一貫するように並べてあるが, 並べ方に制約はない. これを次のように, 右と下に循環させる.
\begin{array}{ccccc}
2&4&6\\
9&5&7&9\\
1&3&8&1&3\\
&4&6\\
&&7\\
\end{array}
ここから次の3つの$3\times3$のブリックを得る.
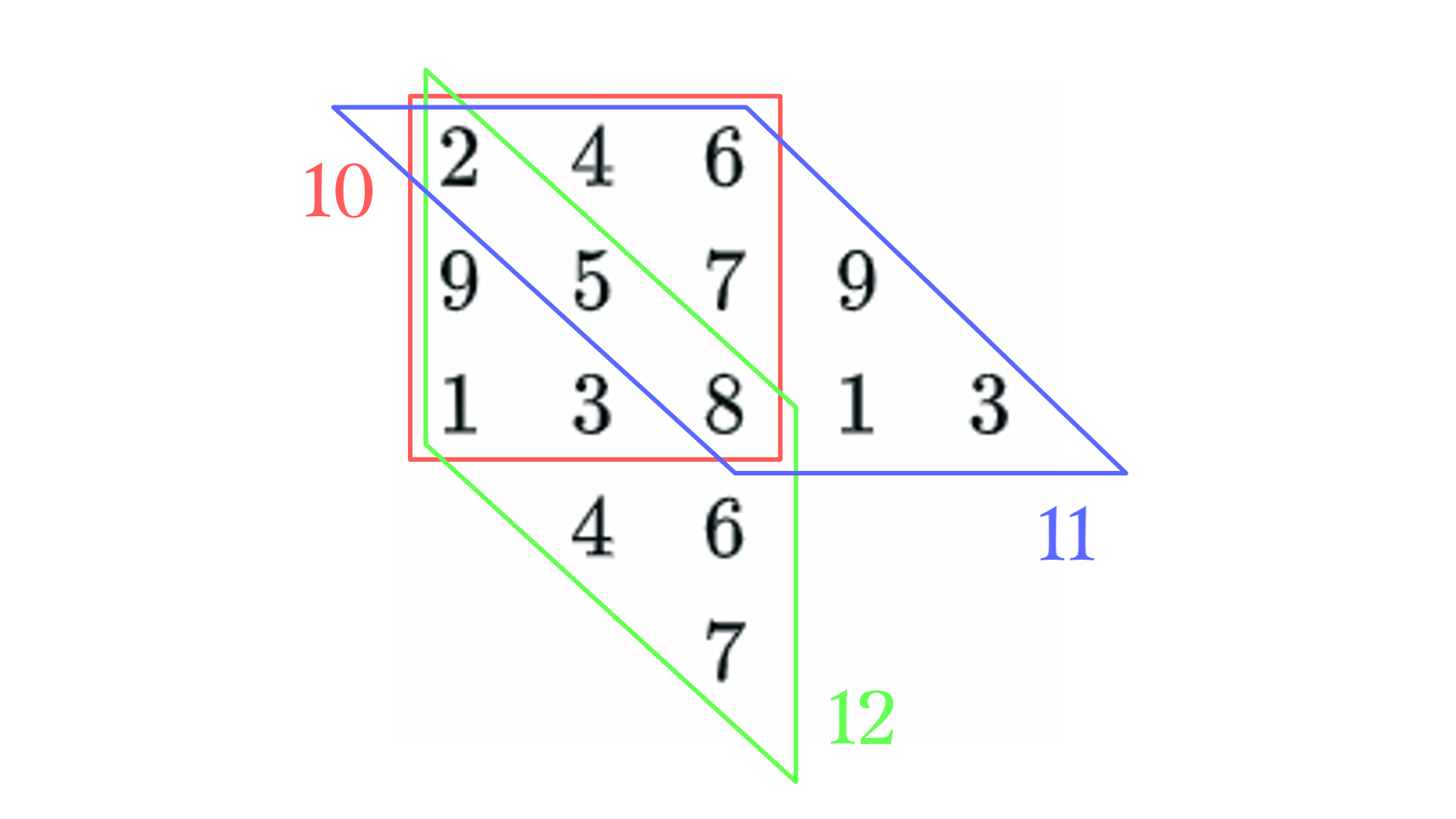
\begin{array}{ccc|ccc|ccc}
&10&&&11&&&12\\\hline
2&4&6&2&4&6&2&5&8\\
9&5&7&5&7&9&9&3&6\\
1&3&8&8&1&3&1&4&7
\end{array}
[i] $10,11,12$が含まれる場合
$3\times3$マスの中の2点と共線上にある点を選べばよい. $(2,7,10,11,12)$を例に取る.
\begin{array}{ccc|ccc|ccc}
\cellcolor{black}&\cellcolor{black}\textcolor{white}{10}&\cellcolor{black}&\cellcolor{black}&\cellcolor{black}\textcolor{white}{11}&\cellcolor{black}&\cellcolor{black}&\cellcolor{black}\textcolor{white}{12}&\cellcolor{black}\\\hline
\cellcolor{black}\textcolor{white}{2}&4&6&\cellcolor{black}\textcolor{white}{2}&4&6&\cellcolor{black}\textcolor{white}{2}&5&8\\
9&5&\cellcolor{black}\textcolor{white}{7}&5&\cellcolor{black}\textcolor{white}{7}&9&9&3&6\\
1&3&8&8&1&3&1&4&\cellcolor{black}\textcolor{white}{7}
\end{array}
$2,3,7$が直線上にあるため, $(2,3,7,10,11,12)$を得る.
[ii] $10,11,12$のうち, 2つが含まれる場合
$(1,3,6,10,12)$を選んだとする.
\begin{array}{ccc|ccc|ccc}
\cellcolor{black}&\cellcolor{black}\textcolor{white}{10}&\cellcolor{black}&&11&&\cellcolor{black}&\cellcolor{black}\textcolor{white}{12}&\cellcolor{black}\\\hline
2&4&6&2&4&\cellcolor{black}\textcolor{white}{6}&2&5&8\\
9&5&7&5&7&9&9&3&6\\
1&3&8&8&\cellcolor{black}\textcolor{white}{1}&\cellcolor{black}\textcolor{white}{3}&1&4&7
\end{array}
$1,3,6$の3箇所が次の18ブリックのいずれかにおいて同色になるよう, ブリックを選んで塗る. 早い話, $S(2,3,9)$で四角形AB(縦横のライン)またはCD(斜めのライン同士)を取ればよい.
\begin{array}{|ccc|ccc|ccc|ccc|ccc|ccc|}\hline
\b&\b&\b&\b&\w&\w&\b&\w&\w&\b&\b&\b&\b&\b&\b&\w&\b&\w\\
\b&\w&\w&\b&\b&\b&\b&\w&\w&\w&\b&\w&\w&\w&\b&\b&\b&\b\\
\b&\w&\w&\b&\w&\w&\b&\b&\b&\w&\b&\w&\w&\w&\b&\w&\b&\w\\\hline
\w&\w&\b&\w&\w&\b&\w&\b&\w&\b&\w&\b&\w&\b&\b&\w&\w&\b\\
\b&\b&\b&\w&\w&\b&\w&\b&\w&\w&\b&\w&\w&\b&\b&\b&\b&\w\\
\w&\w&\b&\b&\b&\b&\b&\b&\b&\b&\w&\b&\b&\w&\w&\b&\b&\w\\\hline
\b&\b&\w&\b&\w&\w&\w&\b&\b&\w&\b&\w&\b&\b&\w&\b&\w&\b\\
\b&\b&\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\w&\b&\b&\w&\b\\
\w&\w&\b&\w&\b&\b&\w&\b&\b&\b&\w&\b&\b&\b&\w&\w&\b&\w\\\hline
\end{array}
該当している
\begin{array}{|ccc|}\hline
\b&\w&\w\\
\b&\b&\b\\
\b&\w&\w\\\hline
\end{array}
の残りのセルを選択し, $(1,3,4,6,10,12)$を得る.
[iii] $10,11,12$のうち, 1つが含まれる場合
$(3,4,7,8,10)$を選んだとする.
\begin{array}{ccc|ccc|ccc}
\cellcolor{black}&\cellcolor{black}\textcolor{white}{10}&\cellcolor{black}&&11&&&12\\\hline
2&4&6&2&\cellcolor{black}\textcolor{white}{4}&6&2&5&8\\
9&5&7&5&\cellcolor{black}\textcolor{white}{7}&9&9&3&6\\
1&3&8&\cellcolor{black}\textcolor{white}{8}&1&\cellcolor{black}\textcolor{white}{3}&1&4&7
\end{array}
同様に, $3,4,7,8$の4箇所が同色になるようブリックを選択する. こちらはクロスABまたはCDとなるように取ればよい.
該当している
\begin{array}{|ccc|}\hline
\w&\b&\w\\
\w&\b&\w\\
\b&\b&\b\\\hline
\end{array}
の残りのセルを選択し, $(1,3,4,7,8,10)$を得る.
[iv] $10,11,12$が含まれていない場合
$(1,3,4,7,9)$を選んだとする. 選択しなかったセルが直線をなすように, 残り1点を確定させる.
\begin{array}{ccc|ccc|ccc}
&10&&&11&&&12\\\hline
2&4&6&2&\cellcolor{black}\textcolor{white}{4}&6&2&5&8\\
9&5&7&5&\cellcolor{black}\textcolor{white}{7}&\cellcolor{black}\textcolor{white}{9}&9&3&6\\
1&3&8&8&\cellcolor{black}\textcolor{white}{1}&\cellcolor{black}\textcolor{white}{3}&1&4&7
\end{array}
この場合$6$を選択すれば, $11$のブリックで$2,5,8$が直線をなすため, $(1,3,4,6,7,9)$を得る.
証明
次の補題は定理1の自然な拡張と捉えられる.
証明
$S$の任意の5点は少なくとも1つの四角形を含み
, $S$の中のある四角形を
\begin{eqnarray}
\Xi=\lbrace\alpha_1,\alpha_2,\alpha_3,\alpha_4\rbrace
\end{eqnarray}
とすると, $\beta\in F\backslash\Xi$は$\Xi$の対角点ではない.
いま, $\Xi$の型を$AB$
\begin{eqnarray}
(\alpha_1,\alpha_2,\alpha_{1\circ2}),(\alpha_3,\alpha_4,\alpha_{3\circ4})\in A\\
(\alpha_1,\alpha_4,\alpha_{1\circ4}),(\alpha_2,\alpha_3,\alpha_{2\circ3})\in B\\
\end{eqnarray}
とすると, $\beta\neq\alpha_{1\circ3}=\alpha_{2\circ4}$.
$\beta=\alpha_{1\circ2}$とすると, 四角形$(\alpha_2,\alpha_3,\alpha_4,\beta)$の対角点は$\alpha_{2\circ3}$で, 四角形$(\alpha_1,\alpha_3,\alpha_4,\beta)$の対角点は$\alpha_{1\circ4}$である.
$\alpha_1\circ\alpha_2=\beta$であるから, この3点を同時に含む四角形は取れない.
以上から, 任意の6点がクロスを含まないという条件を満足するのは$\alpha_{3\circ4}$に限られる.
また, 仮定からこの6点は平行類$A$の異なる2直線である.
\begin{eqnarray}\begin{array}{ll} B_1:\lbrace\alpha,\beta,\gamma\rbrace\cup\Lambda & (\Lambda\in\mathcal{B})\\ B_2:\lbrace\beta,\gamma\rbrace\cup\Xi & (\Xi\in Z_1)\\ B_3:\lbrace\alpha,\gamma\rbrace\cup\Xi & (\Xi\in Z_2)\\ B_4:\lbrace\alpha,\beta\rbrace\cup\Xi & (\Xi\in Z_3)\\ B_5:\lbrace\alpha\rbrace\cup R & (R\in C_1)\\ B_6:\lbrace\beta\rbrace\cup R & (R\in C_2)\\ B_7:\lbrace\gamma\rbrace\cup R & (R\in C_3)\\ B_8:\Lambda_1\cup\Lambda_2 & (\Lambda_1,\Lambda_2\in\mathcal{B},\Lambda_1\cap\Lambda_2=\varnothing) \end{array}\end{eqnarray}
としたとき, $(\Omega\cup\lbrace\alpha,\beta,\gamma\rbrace,\bigcup_{l=1}^{8}B_l)$は$S(5,6,12)$をなす.
$\Omega$の5点集合を$F$とする. $F\in C_i\hspace{2mm}(i=1,2,3)$であれば, $F$は$B_5,B_6,B_7$のいずれかに含まれる.
上の補題から$F\cup\lbrace\gamma\rbrace$の任意の5点がクロスでないような$\delta$が一意に定まり, これは平行な2直線であったから, $F\in B_8$.
残りの場合は$W_{11}$と同様にして示せる.
$W_{11}$のときと同様, 任意の$S(5,6,12)$系に対して3点縮小を取り, 同型射を取ればよい.
$W_{12}$のブロック列挙
クリックして開く
$B\in B_1$に対して, $W_{12}\backslash B\in B_8$.
$B\in B_2$に対して, $B=\Xi\cup\lbrace\beta,\gamma\rbrace$とすると, $W_{12}\backslash B=\Xi^*\cup\lbrace\delta_{\Xi},\alpha\rbrace\in B_5$.
ただし, $\Xi^*$はアフィン平面$W_{12}\backslash\lbrace\alpha,\beta,\gamma\rbrace$において$\Xi$の対角点$\delta_{\Xi}$を共有する唯一の四角形である.
同様に$i=2,3,4$として, $B_i$のブロックの補集合は$B_{i+3}$のブロックとして$W_{12}$に含まれる.
以下で, $W_{12}$の全132ブロックの列挙について, 2つの案を示しておく. 右3マスを$S$からの3点拡大で追加された点, 左9マスをアフィン平面と捉えると整理がつきやすいよう並べているが, $W_{12}$はすべて同型であるからラベルの貼り方に制約はない.
\begin{array}{|cccc|}\hline
00 & 01 & 02 & \alpha\\
10 & 11 & 12 & \beta\\
20 & 21 & 22 & \gamma\\\hline
\end{array}
また, このような$3\times4$のマス目をブリックと呼ぶ.
66ブリック
$W_{12}$のあるブロックの補集合もまた$W_{12}$のブロックであることから, 以下のように$W_{12}$を$\dfrac{132}{2}=66$ブリックとして表す.
黒マス:$\lbrace\alpha,\beta,\gamma\rbrace$と直線($B_1$)
白マス:平行な2直線($B_8$)
\begin{array}{|cccc|cccc|cccc|}\hline
\b&\b&\b&\b&\w&\w&\w&\b&\w&\w&\w&\b\\
\w&\w&\w&\b&\b&\b&\b&\b&\w&\w&\w&\b\\
\w&\w&\w&\b&\w&\w&\w&\b&\b&\b&\b&\b\\\hline
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\\hline
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\
\w&\b&\w&\b&\w&\w&\b&\b&\b&\w&\w&\b\\
\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\b\\\hline
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\
\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\b\\
\w&\b&\w&\b&\w&\w&\b&\b&\b&\w&\w&\b\\\hline
\end{array}
$(00,01,02)$が含まれる平行類を$A$
$(00,10,20)$が含まれる平行類を$B$
$(00,11,22)$が含まれる平行類を$C$
$(00,12,21)$が含まれる平行類を$D$
とする.
黒マス:$\lbrace\beta,\gamma\rbrace$と四角形AB or CD($B_2$)
白マス:$\lbrace\alpha\rbrace$とクロスAB or CD($B_5$)
\begin{array}{|cccc|cccc|cccc|}\hline
\w&\w&\w&\w&\w&\w&\w&\w&\w&\w&\w&\w\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\\hline
\w&\b&\b&\w&\b&\w&\b&\w&\b&\b&\w&\w\\
\w&\w&\w&\b&\w&\w&\w&\b&\w&\w&\w&\b\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\\hline
\w&\b&\b&\w&\b&\w&\b&\w&\b&\b&\w&\w\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\
\w&\w&\w&\b&\w&\w&\w&\b&\w&\w&\w&\b\\\hline
\w&\b&\b&\w&\b&\w&\b&\w&\b&\b&\w&\w\\
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\\hline
\b&\w&\w&\w&\w&\b&\w&\w&\w&\w&\b&\w\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\\hline
\b&\w&\w&\w&\w&\b&\w&\w&\w&\w&\b&\w\\
\b&\w&\w&\b&\w&\b&\w&\b&\w&\w&\b&\b\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\\hline
\end{array}
上9マスが四角形ABとクロスAB, 下9マスが四角形CDとクロスCD.
黒マス:$\lbrace\alpha,\gamma\rbrace$と四角形AD or BC($B_3$)
白マス:$\lbrace\beta\rbrace$とクロスAD or BC($B_6$)
\begin{array}{|cccc|cccc|cccc|}\hline
\w&\w&\w&\b&\w&\w&\w&\b&\w&\w&\w&\b\\
\b&\b&\w&\w&\w&\b&\b&\w&\b&\w&\b&\w\\
\b&\w&\b&\b&\b&\b&\w&\b&\w&\b&\b&\b\\\hline
\b&\b&\w&\b&\b&\b&\w&\b&\w&\b&\b&\b\\
\w&\w&\w&\w&\w&\w&\w&\w&\w&\w&\w&\w\\
\b&\w&\b&\b&\w&\b&\b&\b&\b&\w&\b&\b\\\hline
\b&\b&\w&\b&\w&\b&\b&\b&\b&\w&\b&\b\\
\b&\w&\b&\w&\b&\b&\w&\w&\w&\b&\b&\w\\
\w&\w&\w&\b&\w&\w&\w&\b&\w&\w&\w&\b\\\hline
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\
\w&\w&\b&\w&\b&\w&\w&\w&\w&\b&\w&\w\\
\w&\b&\w&\b&\w&\w&\b&\b&\b&\w&\w&\b\\\hline
\w&\b&\w&\b&\w&\w&\b&\b&\b&\w&\w&\b\\
\w&\b&\b&\w&\b&\w&\b&\w&\b&\b&\w&\w\\
\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\b\\\hline
\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\b\\
\w&\b&\w&\w&\w&\w&\b&\w&\b&\w&\w&\w\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\\hline
\end{array}
上9マスが四角形ABとクロスAD, 下9マスが四角形CDとクロスBC.
黒マス:$\lbrace\alpha,\beta\rbrace$と四角形AC or BD($B_4$)
白マス:$\lbrace\gamma\rbrace$とクロスAC or BD($B_7$)
\begin{array}{|cccc|cccc|cccc|}\hline
\w&\w&\w&\b&\w&\w&\w&\b&\w&\w&\w&\b\\
\b&\w&\b&\b&\b&\b&\w&\b&\w&\b&\b&\b\\
\b&\b&\w&\w&\w&\b&\b&\w&\b&\w&\b&\w\\\hline
\b&\b&\w&\b&\w&\b&\b&\b&\b&\w&\b&\b\\
\w&\w&\w&\b&\w&\w&\w&\b&\w&\w&\w&\b\\
\b&\w&\b&\w&\b&\b&\w&\w&\w&\b&\b&\w\\\hline
\b&\w&\b&\b&\b&\b&\w&\b&\w&\b&\b&\b\\
\b&\b&\w&\b&\w&\b&\b&\b&\b&\w&\b&\b\\
\w&\w&\w&\w&\w&\w&\w&\w&\w&\w&\w&\w\\\hline
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\
\w&\b&\w&\b&\w&\w&\b&\b&\b&\w&\w&\b\\
\w&\w&\b&\w&\b&\w&\w&\w&\w&\b&\w&\w\\\hline
\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\b\\
\w&\b&\b&\b&\b&\w&\b&\b&\b&\b&\w&\b\\
\w&\b&\w&\w&\w&\w&\b&\w&\b&\w&\w&\w\\\hline
\w&\b&\w&\b&\w&\w&\b&\b&\b&\w&\w&\b\\
\w&\w&\b&\b&\b&\w&\w&\b&\w&\b&\w&\b\\
\w&\b&\b&\w&\b&\w&\b&\w&\b&\b&\w&\w\\\hline
\end{array}
31ブリック
マス目の合計が6になるよう, 2つの記号を選ぶとブロックが得られる.
\begin{array}{|cccc|cccc|cccc|cccc|}\hline
\b&\b&\b&\c&\b&\w&\d&\c&\b&\w&\d&\c&\b&\w&\d&\c\\
\w&\w&\w&\c&\b&\w&\d&\c&\d&\b&\w&\c&\w&\d&\b&\c\\
\d&\d&\d&\c&\b&\w&\d&\c&\w&\d&\b&\c&\d&\b&\w&\c\\\hline
\end{array}
\begin{array}{|cccc|cccc|cccc|}\hline
\w&\c&\c&\w&\c&\w&\c&\w&\c&\c&\w&\w\\
\c&\d&\d&\b&\d&\c&\d&\b&\d&\d&\c&\b\\
\c&\d&\d&\b&\d&\c&\d&\b&\d&\d&\c&\b\\\hline
\c&\d&\d&\w&\d&\c&\d&\w&\d&\d&\c&\w\\
\w&\c&\c&\b&\c&\w&\c&\b&\c&\c&\w&\b\\
\c&\d&\d&\b&\d&\c&\d&\b&\d&\d&\c&\b\\\hline
\c&\d&\d&\w&\d&\c&\d&\w&\d&\d&\c&\w\\
\c&\d&\d&\b&\d&\c&\d&\b&\d&\d&\c&\b\\
\w&\c&\c&\b&\c&\w&\c&\b&\c&\c&\w&\b\\\hline
\end{array}
\begin{array}{|cccc|cccc|cccc|}\hline
\w&\c&\c&\b&\c&\w&\c&\b&\c&\c&\w&\b\\
\d&\d&\c&\w&\c&\d&\d&\w&\d&\c&\d&\w\\
\d&\c&\d&\b&\d&\d&\c&\b&\c&\d&\d&\b\\\hline
\d&\c&\d&\b&\d&\d&\c&\b&\c&\d&\d&\b\\
\w&\c&\c&\w&\c&\w&\c&\w&\c&\c&\w&\w\\
\d&\d&\c&\b&\c&\d&\d&\b&\d&\c&\d&\b\\\hline
\d&\d&\c&\b&\c&\d&\d&\b&\d&\c&\d&\b\\
\d&\c&\d&\w&\d&\d&\c&\w&\c&\d&\d&\w\\
\w&\c&\c&\b&\c&\w&\c&\b&\c&\c&\w&\b\\\hline
\end{array}
\begin{array}{|cccc|cccc|cccc|}\hline
\w&\c&\c&\b&\c&\w&\c&\b&\c&\c&\w&\b\\
\d&\c&\d&\b&\d&\d&\c&\b&\c&\d&\d&\b\\
\d&\d&\c&\w&\c&\d&\d&\w&\d&\c&\d&\w\\\hline
\d&\d&\c&\b&\c&\d&\d&\b&\d&\c&\d&\b\\
\w&\c&\c&\b&\c&\w&\c&\b&\c&\c&\w&\b\\
\d&\c&\d&\w&\d&\d&\c&\w&\c&\d&\d&\w\\\hline
\d&\c&\d&\b&\d&\d&\c&\b&\c&\d&\d&\b\\
\d&\d&\c&\b&\c&\d&\d&\b&\d&\c&\d&\b\\
\w&\c&\c&\w&\c&\w&\c&\w&\c&\c&\w&\w\\\hline
\end{array}
このまとめ方には$3^4$型と$2^4$型と呼ばれる分割が背景にある. 文量の事情から本稿では解説を避けるが, 詳細は吉荒yoship.176-178に記載がある.
$M_{12}$の鋭五重推移性と単純性
定理8から$M_{12}$は$W_{12}$に推移的に作用する. $M_{11}$の鋭四重推移性と図式
\begin{xy}\xymatrix{
x_1 \ar[d]^{{}^\exists g\in M_{12}} & (x_2,x_3,x_4,x_5) \ar[d]^{g} & (x_1,x_2,x_3,x_4,x_5) \ar@{.>}[dd]^{{}^{\exists!}f=hg}\\
y_1 \ar[d]^{h} & (z_2,z_3,z_4,z_5) \ar@{.>}[d]^{{}^{\exists!}h\in(M_{12})_{y_1}}\\
y_1 & (y_2,y_3,y_4,y_5) & (y_1,(y_2,y_3,y_4,y_5)
}\end{xy}
により$M_{12}$は鋭五重推移的である.
定理7-系から
\begin{eqnarray}
\#M_{12}=12\cdot11\cdot10\cdot9\cdot8=95040
\end{eqnarray}
$M_{12}$の鋭五重推移性と定理13-系から明らか.
