[i] 明らかに$\Omega'$は$v-1$点集合.
[ii] $S$のブロックから$\alpha$を含むものを取り, そこから$\alpha$を取り除いたものが$\mathcal{B}'$であるから, ${}^{\forall}B\in\mathcal{B}',|B|=k-1$.
[iii] ある$\Omega'$の$t-1$元部分集合を$T$とする. $S(\Omega,\mathcal{B})$はシュタイナーシステムであるから, $T\cup\lbrace\alpha\rbrace$を含むブロック$B\in\mathcal{B}$が存在して一意である. $B$は$B=B'\cup\lbrace\alpha\rbrace$と一意に分解でき,
\begin{eqnarray} {}^{\exists!}T&\in&\Omega',(T\cup\lbrace\alpha\rbrace)\in(B'\cup\lbrace\alpha\rbrace)\\ {}^{\exists!}T&\in&\Omega',T\in B' \end{eqnarray}

　任意のシュタイナーシステムで縮小は存在するが, 拡大が存在するとは限らない.
$S(t,k,v)$が存在するための必要条件は$S(t-1,k-1,v-1)$が存在することであるとも換言できる.

例. $S(3,4,8)$

　$S(2,3,7)$のブロックは以下のように表せた.
\begin{eqnarray}\begin{array}{|cc|}\hline &\cellcolor{#585858}\textcolor{white}{1}\\ 2&3\\ \cellcolor{#585858}\textcolor{white}{4}&\cellcolor{#585858}\textcolor{white}{7}\\ 6&5\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline &\cellcolor{#585858}\textcolor{white}{1}\\ 2&3\\ 4&7\\ \cellcolor{#585858}\textcolor{white}{6}&\cellcolor{#585858}\textcolor{white}{5}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline &1\\ \cellcolor{#585858}\textcolor{white}{2}&3\\ \cellcolor{#585858}\textcolor{white}{4}&7\\ \cellcolor{#585858}\textcolor{white}{6}&5\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline &1\\ \cellcolor{#585858}\textcolor{white}{2}&3\\ 4&\cellcolor{#585858}\textcolor{white}{7}\\ 6&\cellcolor{#585858}\textcolor{white}{5}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline &1\\\ 2&\cellcolor{#585858}\textcolor{white}{3}\\ \cellcolor{#585858}\textcolor{white}{4}&7\\ 6&\cellcolor{#585858}\textcolor{white}{5}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline &1\\ 2&\cellcolor{#585858}\textcolor{white}{3}\\ 4&\cellcolor{#585858}\textcolor{white}{7}\\ \cellcolor{#585858}\textcolor{white}{6}&5\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline &\cellcolor{#585858}\textcolor{white}{1}\\ \cellcolor{#585858}\textcolor{white}{2}&\cellcolor{#585858}\textcolor{white}{3}\\ 4&7\\ 6&5\\\hline \end{array}\end{eqnarray}
左上の空白マスを$\alpha$とし, $\alpha$による一点拡大を考えると, 自明なブロックとして
\begin{eqnarray} \begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&\cellcolor{#585858}\textcolor{white}{1}\\ 2&3\\ \cellcolor{#585858}\textcolor{white}{4}&\cellcolor{#585858}\textcolor{white}{7}\\ 6&5\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&\cellcolor{#585858}\textcolor{white}{1}\\ 2&3\\ 4&7\\ \cellcolor{#585858}\textcolor{white}{6}&\cellcolor{#585858}\textcolor{white}{5}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&1\\ \cellcolor{#585858}\textcolor{white}{2}&3\\ \cellcolor{#585858}\textcolor{white}{4}&7\\ \cellcolor{#585858}\textcolor{white}{6}&5\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&1\\ \cellcolor{#585858}\textcolor{white}{2}&3\\ 4&\cellcolor{#585858}\textcolor{white}{7}\\ 6&\cellcolor{#585858}\textcolor{white}{5}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&1\\ 2&\cellcolor{#585858}\textcolor{white}{3}\\ \cellcolor{#585858}\textcolor{white}{4}&7\\ 6&\cellcolor{#585858}\textcolor{white}{5}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&1\\ 2&\cellcolor{#585858}\textcolor{white}{3}\\ 4&\cellcolor{#585858}\textcolor{white}{7}\\ \cellcolor{#585858}\textcolor{white}{6}&5\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\textcolor{white}{\alpha}&\cellcolor{#585858}\textcolor{white}{1}\\ \cellcolor{#585858}\textcolor{white}{2}&\cellcolor{#585858}\textcolor{white}{3}\\ 4&7\\ 6&5\\\hline \end{array}\hspace{2mm}\end{eqnarray}
が取れるが, 実は黒マスのブロックと黒マスの補集合を合わせれば$S(3,4,8)$のブロックを網羅できている. また, $S(3,4,8)$は次のようにも構成できる.

\begin{eqnarray} \Gamma_3=\lbrace (i,j,k,i+j+k)|i,j,k\in\fif{2}^3,i\neq j\neq k\rbrace \end{eqnarray}
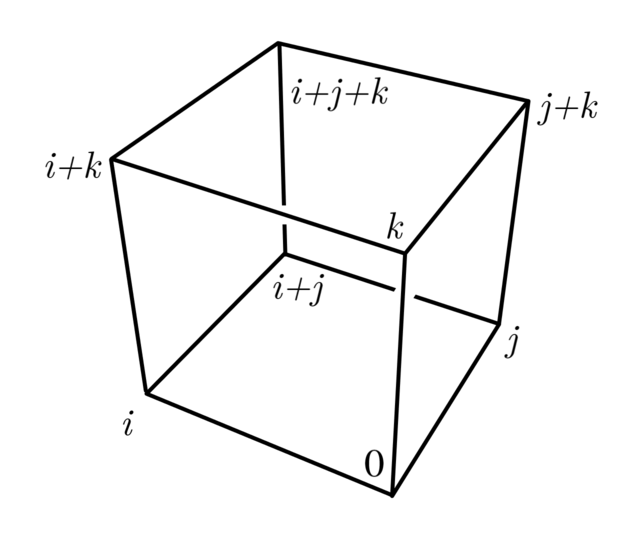
はシュタイナーシステム$S(\fif{2}^3,\Gamma_3)=S(3,4,8)$をなす.

$i,j,k\in\fif{2}^3,i\neq j\neq k$に対して
\begin{eqnarray} i+j+k=i \end{eqnarray}
を仮定すると,
\begin{eqnarray} j+k&=&0\\ j&=&k \end{eqnarray}
と矛盾するため, $i+j+k\neq i$. 同様に$i+j+k\neq j,k$.
したがって, 任意の3つ組$(i,j,k)$に対して$(i,j,k,i+j+k)$が存在して, これは一意である.

　要は, Fig1. のような立方体で平行な辺同士を選択すれば, $S(3,4,8)$のブロックが得られるということである.

Fig1. 有限体上の立方体であることに注意

シュタイナーシステムの自己同型群

定義2　自己同型群

$S\coloneqq S(\Omega,\mathcal{B})$を$S(t,k,v)$系とする. $\sigma\in\sym \Omega,B\in\mathcal{B}$に対して,
\begin{eqnarray} \sigma B=\lbrace\sigma(\alpha)|\alpha\in B\rbrace \end{eqnarray}
と定める. このとき,
\begin{eqnarray} \aut S\coloneqq\lbrace\sigma\in\sym\Omega|{}^{\forall}B\in\mathcal{B},\sigma B\in\mathcal{B}\rbrace \end{eqnarray}
は置換群$\sym\Omega$の部分群であり, $\mathcal{B}$に左から作用する.
このような$\aut S$を$S$の自己同型群とする.

部分群の条件と作用の公理を確認すればよいため, 省略.

例. ファノ平面

　ファノ平面$S(2,3,7)$
\begin{eqnarray} &(1,2,3)&,\hspace{3mm}(2,4,6),\hspace{3mm}(2,5,7)\\ &(1,4,7)&,\hspace{3mm}(3,4,5),\hspace{3mm}(3,6,7)\\ &(1,5,6)& \end{eqnarray}
に対して, $\begin{pmatrix}2&7&5\end{pmatrix}\begin{pmatrix}3&4&6\end{pmatrix}\in\mathfrak{S}_7$はそれぞれのブロックを
\begin{eqnarray} &(1,7,4)&,\hspace{3mm}(7,6,3),\hspace{3mm}(7,2,5)\\ &(1,6,5)&,\hspace{3mm}(4,6,2),\hspace{3mm}(4,3,5)\\ &(1,2,3)& \end{eqnarray}
と動かすため, $\begin{pmatrix}2&7&5\end{pmatrix}\begin{pmatrix}3&4&6\end{pmatrix}\in\aut S(2,3,7)$.
他方, $\begin{pmatrix}1&7&6&5&4&3&2\end{pmatrix}\in\mathfrak{S}_7$は
\begin{eqnarray} \begin{pmatrix}1&7&6&5&4&3&2\end{pmatrix}(1,2,3)=(7,1,2)\notin S(2,3,7) \end{eqnarray}
より$\begin{pmatrix}1&7&6&5&4&3&2\end{pmatrix}\notin\aut S(2,3,7)$

縮小の構造

　シュタイナーシステムにおいて, 縮小と自己同型を取る操作は可換である. ただし, 自己同型群の縮小とは1点を固定して安定化群を得る操作のことで, 厳密には次が成り立つ.

シュタイナーシステム$S\coloneqq S(\Omega,\mathcal{B})$から$\alpha\in\Omega$を取ったとき, $\aut S_\alpha\cong(\aut S)_\alpha$.
ただし,
\begin{eqnarray} (\aut S)_\alpha=\lbrace\sigma\in\aut S|\sigma(\alpha)=\alpha\rbrace \end{eqnarray}

$S_\alpha=S(\Omega\backslash\lbrace\alpha\rbrace,\mathcal{B}')$とする.
$(\mathop{\rm Aut}S)_\alpha$は$\mathcal{B}$に作用するため, $\sigma\in(\aut S)_\alpha$によって定まる写像
\begin{eqnarray} \sigma\colon\mathcal{B}&\longrightarrow&\mathcal{B}\\ B&\longmapsto&\sigma B \end{eqnarray}
は全単射である.
\begin{eqnarray} \phi\colon(\aut S)_\alpha&\longrightarrow&\aut S_\alpha\\ \sigma&\longmapsto&\phi(\sigma) \end{eqnarray}
を
\begin{eqnarray} \phi(\sigma)\colon\mathcal{B}'&\longrightarrow&\mathcal{B}'\\ B\backslash\lbrace\alpha\rbrace&\longmapsto&\sigma B\backslash\lbrace\alpha\rbrace \end{eqnarray}
によって定め, これが全単射準同型であることを示す.
(全射性) 任意の
\begin{eqnarray} \phi(\sigma)\colon\mathcal{B}'&\longrightarrow&\mathcal{B}'\\ B_i&\longmapsto&B_j \end{eqnarray}
に対して, 縮小の定義から
\begin{eqnarray} \sigma\colon\mathcal{B}&\longrightarrow&\mathcal{B}\\ B_i\cup\lbrace\alpha\rbrace&\longmapsto&B_j\cup\lbrace\alpha\rbrace \end{eqnarray}
が存在する.

(単射性)

$B\in\mathcal{B}$, $\sigma, \tau\in(\mathop{\rm Aut}S)_\alpha$に対して, $\sigma B=B',\tau B=B''$とすると, $\sigma(\alpha)=\tau(\alpha)=\alpha$であるから,
\begin{eqnarray} \sigma(B\backslash\lbrace\alpha\rbrace)&=&B'\backslash\lbrace\alpha\rbrace\\ \tau(B\backslash\lbrace\alpha\rbrace)&=&B''\backslash\lbrace\alpha\rbrace\\ \end{eqnarray}
よって,
\begin{eqnarray} \phi(\sigma)&=&\phi(\tau)\\ {}^{\forall}B\backslash\lbrace\alpha\rbrace\in\mathcal{B}',\phi(\sigma)(B\backslash\lbrace\alpha\rbrace)&=&\phi(\tau)(B\backslash\lbrace\alpha\rbrace)\\ B'\backslash\lbrace\alpha\rbrace&=&B''\backslash\lbrace\alpha\rbrace\\ \sigma(B\backslash\lbrace\alpha\rbrace)&=&\tau(B\backslash\lbrace\alpha\rbrace)\\ \sigma&=&\tau \end{eqnarray}

(準同型)

\begin{eqnarray} \phi(\sigma\tau)(B\backslash\lbrace\alpha\rbrace)&=&\sigma\tau(B)\backslash\lbrace\alpha\rbrace\\ &=&\sigma(\tau B)\backslash\lbrace\alpha\rbrace\\ &=&\phi(\sigma)(\tau B\backslash\lbrace\alpha\rbrace)\\ &=&\phi(\sigma)(\phi(\tau)(B\backslash\lbrace\alpha\rbrace))\\ &=&\phi(\sigma)\phi(\tau)(B\backslash\lbrace\alpha\rbrace) \end{eqnarray}
より$\phi(\sigma\tau)=\phi(\sigma)\phi(\tau)$.

拡大の構造

補題3

$S\coloneqq S(\Omega,\mathcal{B})$をシュタイナーシステム, $S$に点$\alpha$を付加して得られた拡大を$S^*$とすると, 単射$\psi\colon\aut S\longrightarrow\aut S^*$が存在して, $\sigma\in\aut S$に対して, $\psi(\sigma)(\alpha)=\alpha$.

安定化群$(\mathop\aut S^*)_\alpha$は$\mathop\aut S^*$の部分群であるから, 埋込$\iota\colon(\aut S^*)_\alpha\hookrightarrow\aut S^*$が存在する. また, constaから$\phi^{-1}\colon\aut S^*_\alpha\longrightarrow(\aut S^*)_\alpha$は同型射である.
以上から, 次の図式を可換にする単射$\psi\coloneqq\iota\circ\phi^{-1}\circ{\rm id}_{\aut S}\colon\aut S\longrightarrow\aut S^*$が存在する.
\begin{xy} \xymatrix {{\rm Aut{\it S}} \ar[d]_{\rm id_{{\rm Aut{\it S}}}} \ar@{_{(}->}[r]^{\psi} & {\rm Aut{\it S}^{*}} \\ {\rm Aut{\it S}^{*}_\alpha} \ar[r]_{\sim}^{\phi^{-1}} & ({\rm Aut}{\it S}^{*})_\alpha \ar@{_{(}->}[u]^{\iota}}\end{xy}
$\iota$は安定化群の埋込であるから, $\sigma\in\aut S$に対して, $\psi(\sigma)(\alpha)=\alpha$.

定理4

$S\coloneqq S(\Omega,\mathcal{B})$をシュタイナーシステム, $S$に点$\alpha$を付加して得られた拡大を$S^*$, $\psi$を補題1の埋込とする.
$S^*=(\Omega\cup\lbrace\alpha\rbrace,\mathcal{B}^*)$として, $\mathcal{B}^*=X\cup\lbrace B\cup\lbrace\alpha\rbrace|B\in\mathcal{B}\rbrace,{}^{\forall}B'\in X, \alpha\notin B'$のように$\mathcal{B}^*$を$\alpha$を含むブロックと含まないブロックに分割したとき, $\aut S\cong\aut S^*$であるための必要十分条件は, ${}^{\forall}B\in X,{}^{\forall}\sigma\in\aut S,\psi(\sigma)\in X$.

(必要であること)

$\psi$が同型射だと措定したため, $\sigma,\tau\in\aut S$に対して$\psi(\sigma\tau)=\psi(\sigma)\psi(\tau)$
$B\in X$に対して, $\psi(\sigma)B=B'\cup\lbrace\alpha\rbrace$なる$\sigma\in\aut S$が存在すると仮定すると,
\begin{eqnarray} \psi(\sigma^{-1}\sigma)B&=&\psi(\sigma)^{-1}(\psi(\sigma)B)\\ &=&\psi(\sigma)^{-1}(B'\cup\lbrace\alpha\rbrace)\\ B&=&\psi(\sigma)^{-1}B'\cup\lbrace\alpha\rbrace\\ &\notin&X \end{eqnarray}
となり, $B\in X$と矛盾するため, $\psi(\sigma)$は$X$のブロックを$X$のブロックに移す.
(十分であること)
$\psi$が全射準同型であることを確認すればよいため, 省略.

定理4-系

$S\coloneqq S(\Omega,\mathcal{B})$をシュタイナーシステム, $S$に点$\alpha$を付加して得られた拡大を$S^*$とする. $S^*=(\Omega\cup\lbrace\alpha\rbrace,\mathcal{B}^*)$として, $\mathcal{B}^*=X\cup\lbrace B\cup\lbrace\alpha\rbrace|B\in\mathcal{B}\rbrace,{}^{\forall}B'\in X, \alpha\notin B'$のように$\mathcal{B}^*$を$\alpha$を含むブロックと含まないブロックに分割したとき, ${\rm Aut}S$の生成系を$L$とすると, ${}^{\forall}l\in L,{}^{\forall}B\in X, lX\in X$ならば$\aut S\cong\aut S^*$.

$L$の元が$\aut S$全体を生成することから直ちに従う.

　実用上は定理2の十分条件が重要で, 系から$\aut S\cong\aut S^*$の判定に要する計算量が大幅に減る.

例. ファノ平面の1点拡大

　ファノ平面の1点拡大$S(3,4,8)$について, ブロックを列挙すると,
\begin{eqnarray} &(1,2,3,8)&,\hspace{3mm}(2,4,6,8),\hspace{3mm}(2,5,7,8)\\ &(1,4,7,8)&,\hspace{3mm}(3,4,5,8),\hspace{3mm}(3,6,7,8)\\ &(1,5,6,8)&,\\ &(1,2,4,5)&,\hspace{3mm}(1,3,4,6),\hspace{3mm}(2,3,4,7)\\ &(1,2,6,7)&,\hspace{3mm}(1,3,5,7),\hspace{3mm}(2,3,5,6)\\ &(4,5,6,7)& \end{eqnarray}
この中で拡大により追加されたブロックは
\begin{eqnarray} &(1,2,4,5)&,\hspace{3mm}(1,3,4,6),\hspace{3mm}(2,3,4,7)\\ &(1,2,6,7)&,\hspace{3mm}(1,3,5,7),\hspace{3mm}(2,3,5,6)\\ &(4,5,6,7)& \end{eqnarray}
の7つである. ファノ平面の自己同型群は$\aut S(2,3,7)=\langle\mqty(1&2)\mqty(6&7),\mqty(2&7&5)\mqty(3&4&6)\rangle$の2元生成であるから, $2\cdot7=14$回の計算で$\aut S(2,3,7)$と$\aut S(3,4,8)$が同型かどうか判別できる. 実際, 生成元は追加されたブロックを外に移さないことから,
\begin{eqnarray} \aut S(2,3,7)\cong\aut S(3,4,8) \end{eqnarray}
が成り立つ.