5次元超立方体とS(3,4,32)

1. フィッシャー不等式


2. 算術三角形


3. 自己同型群と拡大・縮小


4. アフィン平面
   
   
   
   1. 相互直交ラテン方格
   
   


5. シュタイナー三重系
   
   
   
   1. STSの直積
   
   


6. マシュー群 $M_{11}$と$M_{12}$
   
   
   
   1. $S(2,3,9)$の性質
   
   
   2. $S(3,4,10)$の構成
   
   
   3. $M_{11}$と$M_{12}$
   
   


7. 射影平面
   
   
   
   1. ブルック-ライサーの定理
   
   


8. シュタイナー四重系
   
   
   
   1. 正測体とSQS
   
   

　本稿では$S_5\coloneqq S(3,4,32)$について,

1. 二元体$\mathbb{F}_2$による構成
2. アルゴリズム的な構成
3. 5次元超立方体を用いた構成

を試みる. 今回の方法は$S_n\coloneqq S(3,4,2^n)$一般に通用するものだが, 適度なサイズの$n=5$をピックアップしている. 構成法も定理の証明も大部分は管見によるものゆえ冗長性を取り除けていない可能性があることに注意.

代数的な構成

　以下, 3つ組$(\alpha,\beta,\gamma)$が含まれる唯一のブロックを$(\alpha,\beta,\gamma,\alpha\circ\beta\circ\gamma)$と表記する.

　要するに,

　定理1　：　${\mathbb{F}}^n$に対してシュタイナーシステムの構造を定める
　定理2　：　$S_{n-1}$から帰納的に$S_n$を定める

となっていて, 定理2の構成法を$S_3$から始めて$S_3\rightarrow S_4\rightarrow S_5\rightarrow \cdots$と順繰りに構成したものがすべて定理1の構成法と等価だと主張している. また, 補題3から, どのような$S_3$を起点としても再帰的な構成は一意であることが分かる.

アルゴリズム的な構成

　本記事の準目玉で, $S_3=S(3,4,8)$を拡張し, $S_5$を得ようという方針. $S(5,8,24)$の構成法として有名なカーティスのMOGcurtisというアルゴリズムに感化されている部分が大きい. 構成法を一通り見た後で, 原理と定理2との関係について説明する.

$S_3$と$4\times2$ブリック

　まずは, 次のような8つの$4\times2$のマスを考える.
\begin{array}{|cc|cc|cc|cc|}\hline 1&2&\blacksquare&\blacksquare&\square&\blacksquare&\blacksquare&\blacksquare\\ 3&4&\blacksquare&\blacksquare&\square&\blacksquare&\square&\square\\ 5&6&\square&\square&\square&\blacksquare&\blacksquare&\blacksquare\\ 7&8&\square&\square&\square&\blacksquare&\square&\square\\\hline \square&\blacksquare&\square&\blacksquare&\square&\blacksquare&\blacksquare&\blacksquare\\ \blacksquare&\square&\blacksquare&\square&\square&\blacksquare&\square&\square\\ \square&\blacksquare&\blacksquare&\square&\blacksquare&\square&\square&\square\\ \blacksquare&\square&\square&\blacksquare&\blacksquare&\square&\blacksquare&\blacksquare\\\hline \end{array}
本家に倣い, それぞれの$4\times2$の区域をブリック ( bricks ) と呼ぶ. この表を用いれば, 1から8までの任意の3つの数字から$S_3$のブロックが決定できる.
例えば, $4,7,8$を選んだとすると
\begin{array}{|cc|}\hline 1&2\\ 3&\cellcolor{#585858}\textcolor{white}{4}\\ 5&6\\ \cellcolor{#585858}\textcolor{white}{7}&\cellcolor{#585858}\textcolor{white}{8}\\\hline \end{array}
となり, この3箇所が同じ色で塗られているブリックを探すと,
\begin{array}{|cc|}\hline \blacksquare&\blacksquare\\ \square&\square\\ \blacksquare&\blacksquare\\ \square&\square\\\hline \end{array}
が見つかる. $4,7,8$が該当しているのは白マスの方で, 4マスある白マスのうち, もとのブリックで塗られていなかった数字を塗れば4つ組$(3,4,7,8)$が得られる.

\begin{array}{|cc|cc|}\hline 1&2&\blacksquare&\blacksquare\\ \cellcolor{#585858}\textcolor{white}{3}&\cellcolor{#585858}\textcolor{white}{4}&\w&\w\\ 5&6&\blacksquare&\blacksquare\\ \cellcolor{#585858}\textcolor{white}{7}&\cellcolor{#585858}\textcolor{white}{8}&\w&\w\\\hline \end{array}

塗りつぶしのパターンは14通りあり,

\begin{eqnarray} \begin{array}{|cc|}\hline \cellcolor{#585858}\tw{1}&\cellcolor{#585858}\tw{2}\\ \cellcolor{#585858}\tw{3}&\cellcolor{#585858}\tw{4}\\ 5&6\\ 7&8\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline 1&\cellcolor{#585858}\tw{2}\\ 3&\cellcolor{#585858}\tw{4}\\ 5&\cellcolor{#585858}\tw{6}\\ 7&\cellcolor{#585858}\tw{8}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{1}&\cellcolor{#585858}\tw{2}\\ 3&4\\ \cellcolor{#585858}\tw{5}&\cellcolor{#585858}\tw{6}\\ 7&8\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline 1&\cellcolor{#585858}\tw{2}\\ \cellcolor{#585858}\tw{3}&4\\ 5&\cellcolor{#585858}\tw{6}\\ \cellcolor{#585858}\tw{7}&8\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline 1&\cellcolor{#585858}\tw{2}\\ \cellcolor{#585858}\tw{3}&4\\ \cellcolor{#585858}\tw{5}&6\\ 7&\cellcolor{#585858}\tw{8}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline 1&\cellcolor{#585858}\tw{2}\\ 3&\cellcolor{#585858}\tw{4}\\ \cellcolor{#585858}\tw{5}&6\\ \cellcolor{#585858}\tw{7}&8\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{1}&\cellcolor{#585858}\tw{2}\\ 3&4\\ 5&6\\ \cellcolor{#585858}\tw{7}&\cellcolor{#585858}\tw{8}\\\hline \end{array}\hspace{2mm} \end{eqnarray}

\begin{eqnarray} S_3=\lbrace(1,2,3,4),(1,2,5,6),(1,3,5,7),(2,4,6,8),\\ (3,4,7,8),(5,6,7,8),(1,2,7,8),(1,3,6,8),\\ (3,4,5,6),(2,4,5,7),(1,4,5,8),(2,3,6,7),\\ (1,4,6,7),(2,3,5,8)\rbrace \end{eqnarray}
となる.

$S_4$と$4\times4$ブリック

　$S_3$のブリックを拡張すると, 以下のような36個のブリックが得られる.
\begin{array}{|cccc|cccc|cccc|cccc|cccc|cccc|}\hline 1&2&9&10&\b&\b&\c&\c&\w&\b&\d&\c&\b&\b&\c&\c&\w&\b&\d&\c&\w&\b&\d&\c\\ 3&4&11&12&\b&\b&\c&\c&\w&\b&\d&\c&\w&\w&\d&\d&\b&\w&\c&\d&\b&\w&\c&\d\\ 5&6&13&14&\w&\w&\d&\d&\w&\b&\d&\c&\b&\b&\c&\c&\w&\b&\d&\c&\b&\w&\c&\d\\ 7&8&15&16&\w&\w&\d&\d&\w&\b&\d&\c&\w&\w&\d&\d&\b&\w&\c&\d&\w&\b&\d&\c\\\hline \w&\b&\d&\c&\b&\b&\c&\c&\b&\b&\c&\c&\w&\b&\d&\c&\b&\b&\c&\c&\w&\b&\d&\c\\ \w&\b&\d&\c&\w&\w&\d&\d&\c&\c&\b&\b&\w&\b&\d&\c&\w&\w&\d&\d&\b&\w&\c&\d\\ \b&\w&\c&\d&\w&\w&\d&\d&\w&\w&\d&\d&\d&\c&\w&\b&\c&\c&\b&\b&\d&\c&\w&\b\\ \b&\w&\c&\d&\b&\b&\c&\c&\d&\d&\w&\w&\d&\c&\w&\b&\d&\d&\w&\w&\c&\d&\b&\w\\\hline \w&\b&\d&\c&\w&\b&\d&\c&\b&\b&\w&\w&\b&\c&\c&\b&\w&\b&\d&\c&\b&\c&\c&\b\\ \b&\w&\c&\d&\w&\b&\d&\c&\d&\d&\c&\c&\b&\c&\c&\b&\d&\c&\w&\b&\w&\d&\d&\w\\ \c&\d&\b&\w&\c&\d&\b&\w&\c&\c&\d&\d&\w&\d&\d&\w&\w&\b&\d&\c&\b&\c&\c&\b\\ \d&\c&\w&\b&\c&\d&\b&\w&\w&\w&\b&\b&\w&\d&\d&\w&\d&\c&\w&\b&\w&\d&\d&\w\\\hline \w&\b&\d&\c&\b&\c&\c&\b&\w&\b&\d&\c&\w&\b&\d&\c&\w&\b&\d&\c&\b&\c&\c&\b\\ \c&\d&\b&\w&\c&\b&\b&\c&\d&\c&\w&\b&\c&\d&\b&\w&\d&\c&\w&\b&\w&\d&\d&\w\\ \w&\b&\d&\c&\w&\d&\d&\w&\d&\c&\w&\b&\c&\d&\b&\w&\c&\d&\b&\w&\d&\w&\w&\d\\ \c&\d&\b&\w&\d&\w&\w&\d&\w&\b&\d&\c&\w&\b&\d&\c&\b&\w&\c&\d&\c&\b&\b&\c\\\hline \b&\c&\c&\b&\w&\b&\d&\c&\b&\b&\b&\b&\w&\b&\w&\b&\b&\c&\b&\c&\b&\c&\b&\c\\ \w&\d&\d&\w&\c&\d&\b&\w&\w&\w&\w&\w&\b&\w&\b&\w&\w&\d&\w&\d&\w&\d&\w&\d\\ \c&\b&\b&\c&\d&\c&\w&\b&\c&\c&\c&\c&\d&\c&\d&\c&\w&\d&\w&\d&\d&\w&\d&\w\\ \d&\w&\w&\d&\b&\w&\c&\d&\d&\d&\d&\d&\c&\d&\c&\d&\b&\c&\b&\c&\c&\b&\c&\b\\\hline \w&\b&\w&\b&\b&\c&\b&\c&\b&\c&\b&\c&\b&\w&\c&\d&\b&\w&\d&\c&\b&\w&\w&\b\\ \w&\b&\w&\b&\w&\d&\w&\d&\w&\d&\w&\d&\d&\c&\w&\b&\d&\c&\b&\w&\d&\c&\c&\d\\ \d&\c&\d&\c&\b&\c&\b&\c&\c&\b&\c&\b&\w&\b&\d&\c&\w&\b&\c&\d&\d&\c&\c&\d\\ \d&\c&\d&\c&\w&\d&\w&\d&\d&\w&\d&\w&\c&\d&\b&\w&\c&\d&\w&\b&\b&\w&\w&\b\\\hline \end{array}
下で利用する際に再度画像を貼る.

$S_5$への拡張

\begin{array}{|cccc|cccc|}\hline 1&2&9&10&17&18&25&26\\ 3&4&11&12&19&20&27&28\\ 5&6&13&14&21&22&29&30\\ 7&8&15&16&23&24&31&32\\\hline \end{array}
　2つの数字のブリックを$S_4$の35個のブリックに当てはめて$S_5$のブロックを探す. 基本的なルールとして, 1つのブリックに数字は偶数個入る. 例えば, $10,20,32$を選んだとして, $20,32$は右のブリック, $10$は左のブリックに入っているため, 残りひとつは左のブリックから決めることになる. 続けて, 数字を確定させる. まずは, 空の$4\times4$ブリックを持ってきて, 左のブリックに重ね, $10$の位置を塗る.
\begin{array}{|cccc|}\hline \w&\w&\w&\b\\ \w&\w&\w&\w\\ \w&\w&\w&\w\\ \w&\w&\w&\w\\\hline \end{array}
右のブリックにも重ねて, $20,32$の位置を塗る.
\begin{array}{|cccc|}\hline \w&\w&\w&\b\\ \w&\b&\w&\w\\ \w&\w&\w&\w\\ \w&\w&\w&\b\\\hline \end{array}
この3箇所に同じ図形が配置されている$S_4$のブリックを探すと,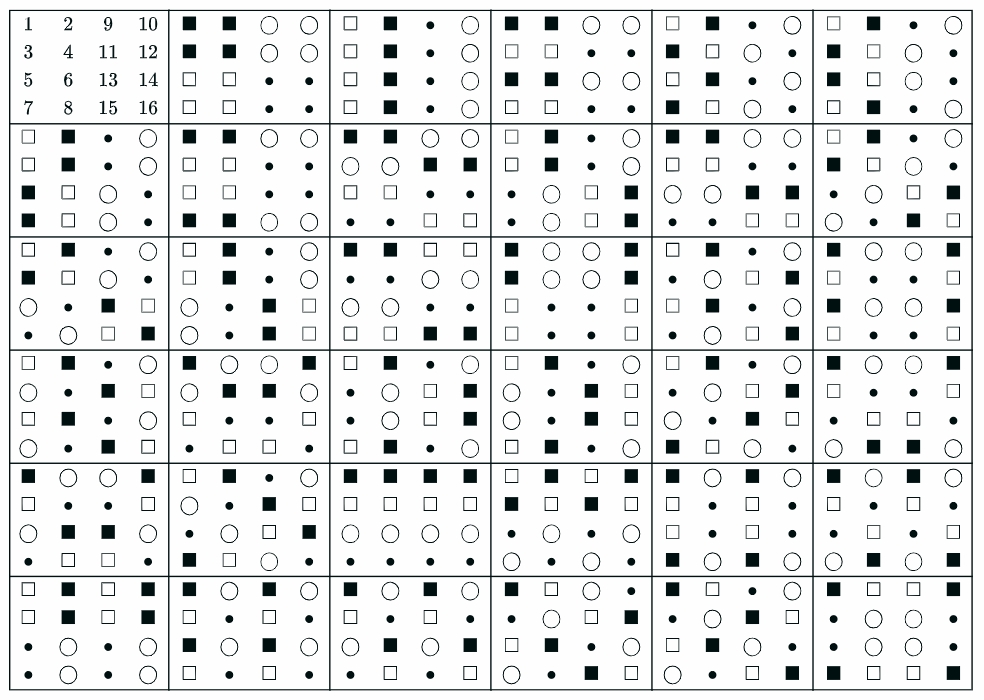

\begin{array}{|cccc|}\hline \w&\b&\d&\c\\ \d&\c&\w&\b\\ \d&\c&\w&\b\\ \w&\b&\d&\c\\\hline \end{array}
が見つかる. この場合塗った3マスは$\c$に対応していて, 塗られていなかったマスの位置は
\begin{array}{|cccc|}\hline \w&\w&\w&\w\\ \w&\w&\w&\w\\ \w&\b&\w&\w\\ \w&\w&\w&\w\\\hline \end{array}
で, $10$があったブリックから数字を選ぶことを思い出せば, この位置にある$6$が得られる.
\begin{array}{|cccc|cccc|}\hline 1&2&9&\cellcolor{#585858}\textcolor{white}{10}&17&18&25&26\\ 3&4&11&12&19&\cellcolor{#585858}\textcolor{white}{20}&27&28\\ 5&\cellcolor{#585858}\textcolor{white}{6}&13&14&21&22&29&30\\ 7&8&15&16&23&24&31&\cellcolor{#585858}\textcolor{white}{32}\\\hline \end{array}
次は$9,14,25$を選ぶ. 同じ要領で空のブリックに色を付けると
\begin{array}{|cccc|}\hline \w&\w&\b&\w\\ \w&\w&\w&\w\\ \w&\w&\w&\b\\ \w&\w&\w&\w\\\hline \end{array}
と, 2箇所しか塗れないが, この場合はそのまま右のブリックに当てはめて$25$を得る.
\begin{array}{|cccc|cccc|}\hline 1&2&\cellcolor{#585858}\textcolor{white}{9}&10&17&18&\cellcolor{#585858}\textcolor{white}{25}&26\\ 3&4&11&12&19&20&27&28\\ 5&6&13&\cellcolor{#585858}\textcolor{white}{14}&21&22&29&\cellcolor{#585858}\textcolor{white}{30}\\ 7&8&15&16&23&24&31&32\\\hline \end{array}

　ブリックの数は$S_3$では8個, $S_4$では36個だったが, $S_5$では156個のブリックが必要になってしまう.

原理

　この構成法は定理2を可視化したものになっている. 定理2を振り返りつつ, どのようにして$S_3$の7つのブリックを得るかを見ていく.

\begin{eqnarray}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&(1,1)\\ \cellcolor{#585858}\tw{(0,2)}&(1,2)\\ \cellcolor{#585858}\tw{(0,3)}&(1,3)\\ \cellcolor{#585858}\tw{(0,4)}&(1,4)\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&\cellcolor{#585858}\tw{(1,1)}\\ (0,2)&\cellcolor{#585858}\tw{(1,2)}\\ (0,3)&\cellcolor{#585858}\tw{(1,3)}\\ (0,4)&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&(1,1)\\ \cellcolor{#585858}\tw{(0,2)}&(1,2)\\ (0,3)&\cellcolor{#585858}\tw{(1,3)}\\ (0,4)&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&\cellcolor{#585858}\tw{(1,1)}\\ (0,2)&\cellcolor{#585858}\tw{(1,2)}\\ \cellcolor{#585858}\tw{(0,3)}&(1,3)\\ \cellcolor{#585858}\tw{(0,4)}&(1,4)\\\hline \end{array}\\\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&(1,1)\\ (0,2)&\cellcolor{#585858}\tw{(1,2)}\\ (0,3)&\cellcolor{#585858}\tw{(1,3)}\\ \cellcolor{#585858}\tw{(0,4)}&(1,4)\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&\cellcolor{#585858}\tw{(1,1)}\\ \cellcolor{#585858}\tw{(0,2)}&(1,2)\\ \cellcolor{#585858}\tw{(0,3)}&(1,3)\\ (0,4)&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&(1,1)\\ (0,2)&\cellcolor{#585858}\tw{(1,2)}\\ \cellcolor{#585858}\tw{(0,3)}&(1,3)\\ (0,4)&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&\cellcolor{#585858}\tw{(1,1)}\\ \cellcolor{#585858}\tw{(0,2)}&(1,2)\\ (0,3)&\cellcolor{#585858}\tw{(1,3)}\\ \cellcolor{#585858}\tw{(0,4)}&(1,4)\\\hline \end{array}\end{eqnarray}

$((0,x),(0,y),(1,x),(1,y))$の形のブロックは

\begin{eqnarray}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&\cellcolor{#585858}\tw{(1,1)}\\ \cellcolor{#585858}\tw{(0,2)}&\cellcolor{#585858}\tw{(1,2)}\\ (0,3)&(1,3)\\(0,4)&(1,4)\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&\cellcolor{#585858}\tw{(1,1)}\\ (0,2)&(1,2)\\ \cellcolor{#585858}\tw{(0,3)}&\cellcolor{#585858}\tw{(1,3)}\\ (0,4)&(1,4)\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&\cellcolor{#585858}\tw{(1,1)}\\ (0,2)&(1,2)\\(0,3)&(1,3)\\ \cellcolor{#585858}\tw{(0,4)}&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\\\begin{array}{|cc|}\hline (0,1)&(1,1)\\ \cellcolor{#585858}\tw{(0,2)}&\cellcolor{#585858}\tw{(1,2})\\ \cellcolor{#585858}\tw{(0,3)}&\cellcolor{#585858}\tw{(1,3)}\\ (0,4)&(1,4)\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&(1,1)\\ \cellcolor{#585858}\tw{(0,2)}&\cellcolor{#585858}\tw{(1,2)}\\ (0,3)&(1,3)\\ \cellcolor{#585858}\tw{(0,4)}&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&(1,1)\\(0,2)&(1,2)\\ \cellcolor{#585858}\tw{(0,3)}&\cellcolor{#585858}\tw{(1,3)}\\ \cellcolor{#585858}\tw{(0,4)}&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\end{eqnarray}

と14個のブロックを列挙できているが, 例えば
\begin{eqnarray}\begin{array}{|cc|}\hline \cellcolor{#585858}\tw{(0,1)}&(1,1)\\\cellcolor{#585858}\tw{(0,2)}&(1,2)\\\cellcolor{#585858}\tw{(0,3)}&(1,3)\\\cellcolor{#585858}\tw{(0,4)}&(1,4)\\\hline \end{array}\hspace{2mm}\begin{array}{|cc|}\hline (0,1)&\cellcolor{#585858}\tw{(1,1)}\\(0,2)&\cellcolor{#585858}\tw{(1,2)}\\(0,3)&\cellcolor{#585858}\tw{(1,3)}\\(0,4)&\cellcolor{#585858}\tw{(1,4)}\\\hline \end{array}\end{eqnarray}

の2ブロックは$\mathbb{F}_2\times S_2$において, 互いに補集合の関係になっている. このような2ブロックを1ブリックにまとめると, 求めていた8ブリック
\begin{array}{|cc|cc|cc|cc|}\hline 1&2&\blacksquare&\blacksquare&\square&\blacksquare&\blacksquare&\blacksquare\\ 3&4&\blacksquare&\blacksquare&\square&\blacksquare&\square&\square\\ 5&6&\square&\square&\square&\blacksquare&\blacksquare&\blacksquare\\ 7&8&\square&\square&\square&\blacksquare&\square&\square\\\hline \square&\blacksquare&\square&\blacksquare&\square&\blacksquare&\blacksquare&\blacksquare\\ \blacksquare&\square&\blacksquare&\square&\square&\blacksquare&\square&\square\\ \square&\blacksquare&\blacksquare&\square&\blacksquare&\square&\square&\square\\ \blacksquare&\square&\square&\blacksquare&\blacksquare&\square&\blacksquare&\blacksquare\\\hline \end{array}
が得られる. $\Gamma_n$のブロックの数は
\begin{eqnarray} |\Gamma_n|=\frac{2^n(2^n-1)(2^n-2)}{4\cdot3\cdot2}=\frac{2^{n-2}(2^{n-1}-1)(2^n-1)}{3} \end{eqnarray}
だが, $\Gamma_n$のブリックの数$\mathfrak{R}_n$は
\begin{eqnarray} \mathfrak{R}_n&=&\frac{1}{2^{n-2}}|\Gamma_n|\\ &=&\frac{(2^{n-1}-1)(2^n-1)}{3} \end{eqnarray}
と, 相補的なブリックにすることで大分コンパクトになっている.

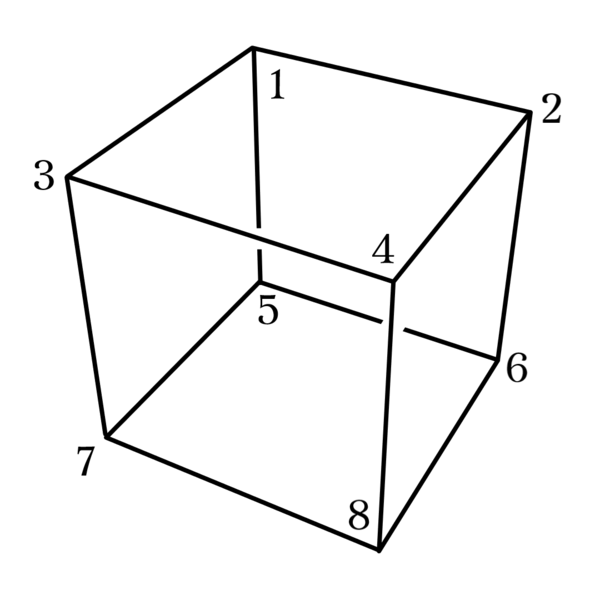
5次元超立方体を用いた構成

　上の方法と同様, まずは$S_3$を立方体から構成し, それを$S_5$へと拡張する.

$S_3$と立方体

　Fig1. で$1,5,7$のように同一平面内にある3点を選んだときはその面の残りの点を選択する. これにより
\begin{eqnarray} (1,2,3,4),(1,2,5,6),(1,3,5,7),\\ (2,4,6,8),(3,4,7,8),(5,6,7,8) \end{eqnarray}
を得, $2,4,5$のように$2,4$が辺で結ばれているときには, その辺と平行な辺で$5$を含む辺を選び, $(2,4,5,7)$とする. 立方体を二分する断面とも見れ, このタイプの4つ組を列挙すると
\begin{eqnarray} (1,2,7,8),(1,3,6,8),(3,4,5,6),\\ (2,4,5,7),(1,4,5,8),(2,3,6,7) \end{eqnarray}
最後にどの2点も辺上にないような$1,6,7$に対しては, その性質を保存する$4$を取る. これは2通り挙げられ,
\begin{eqnarray} (1,4,6,7),(2,3,5,8) \end{eqnarray}
以上をまとめると
\begin{eqnarray} S_3=\lbrace(1,2,3,4),(1,2,5,6),(1,3,5,7),(2,4,6,8),\\ (3,4,7,8),(5,6,7,8),(1,2,7,8),(1,3,6,8),\\ (3,4,5,6),(2,4,5,7),(1,4,5,8),(2,3,6,7),\\ (1,4,6,7),(2,3,5,8)\rbrace \end{eqnarray}
と, $\dfrac{\mqty(8\\3)}{\mqty(4\\3)}=14$個のブロックを列挙できた.
以下ではこの方法を5次元へと持ち込むことになる.

$S_5$への拡張

　立方体を重ねた4次元多胞体が超立方体(テッセラクト, 正八胞体とも)であり, それをさらに重ねた5次元超立方体を$T_5$とする. $T_5$には10個のテッセラクト, 40個の立方体が含まれていて, 頂点数は32となっている.

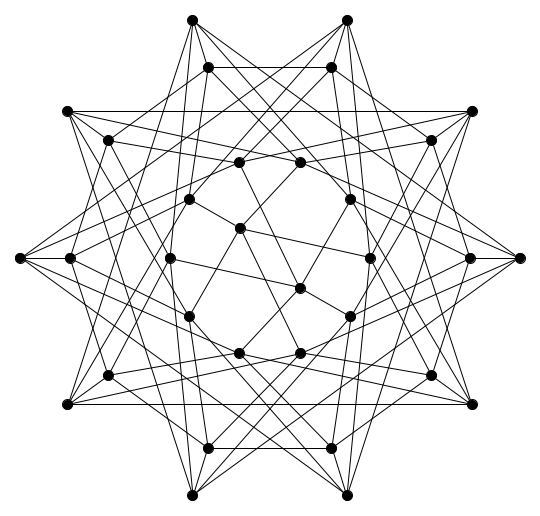
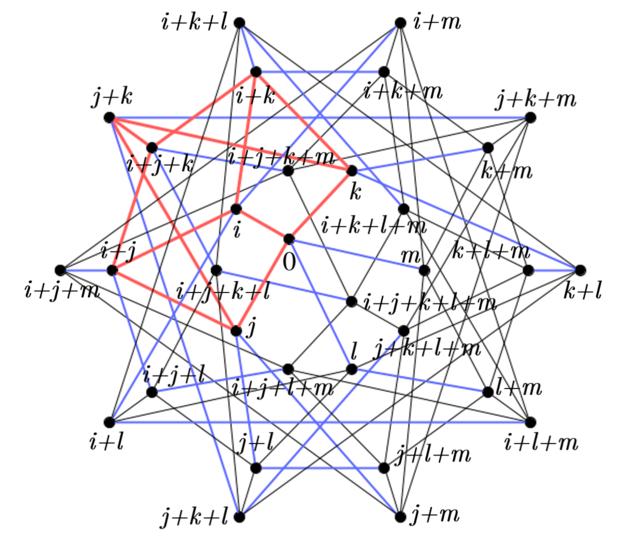
ここで, 次のような辺彩色を施した2つのグラフを考える.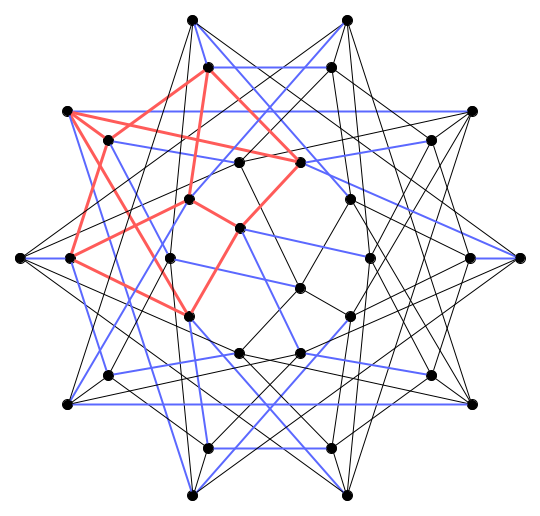

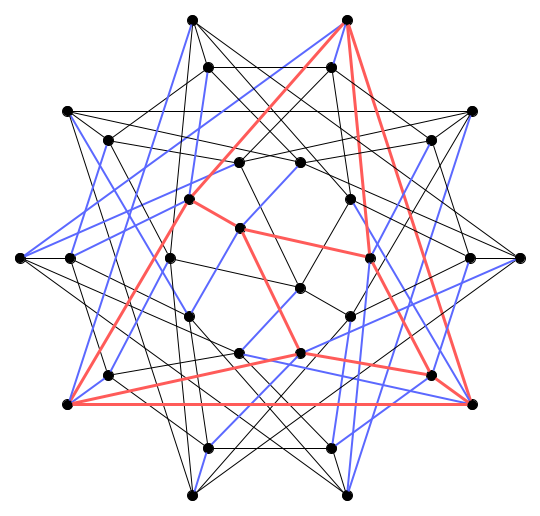
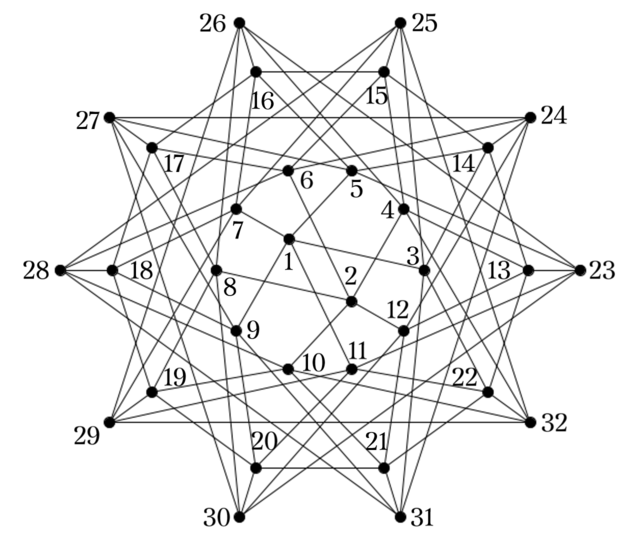
　このような彩色をする理由は後述するとして, 実際に3点から残り1点を決める過程を説明する. $C_1,C_2$をよく観察すると, すべての点が赤い辺か青い辺の上にあることが確認できる. 選んだ3点について, 赤い辺の上にあった場合はそのまま, 青い辺上にあった場合は青い辺をつたって赤い辺上の点まで移動する. 赤い辺は立方体になっているため, そこで$S_3$のときと同じ操作で残り1点を得るが, これで確定というわけではなく, その点から青い辺をつたって移動できる場所4つが候補となる. これを$C_1,C_2$で行えば共通している1点が得られる.
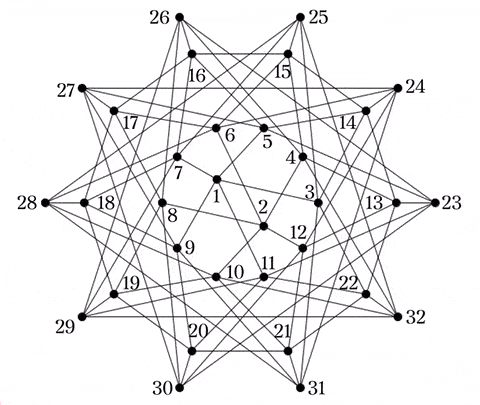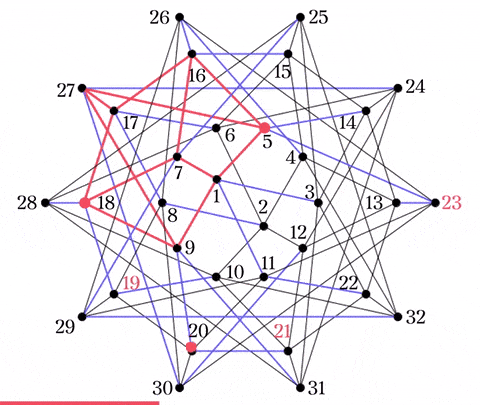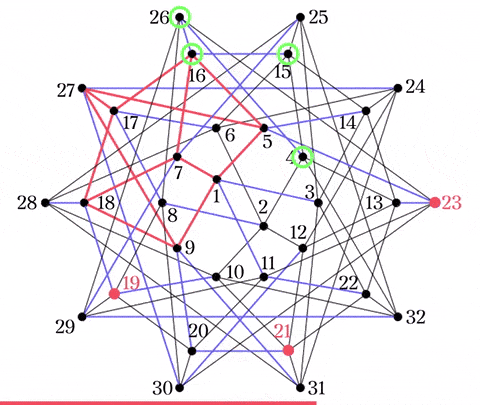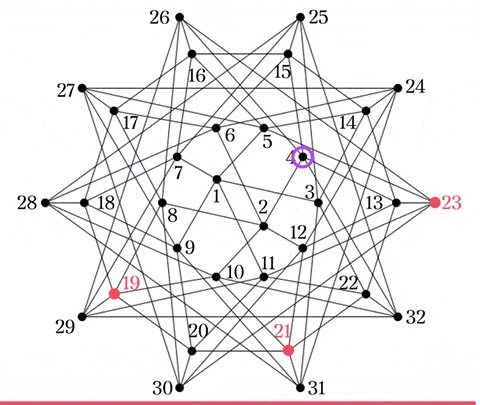
　試しに$19,21,23$をFig5. から選んだときの残り1点を求めてみる.

1.　赤の辺に点を移す

　$19,21,23$を$C_1$にプロットすると,

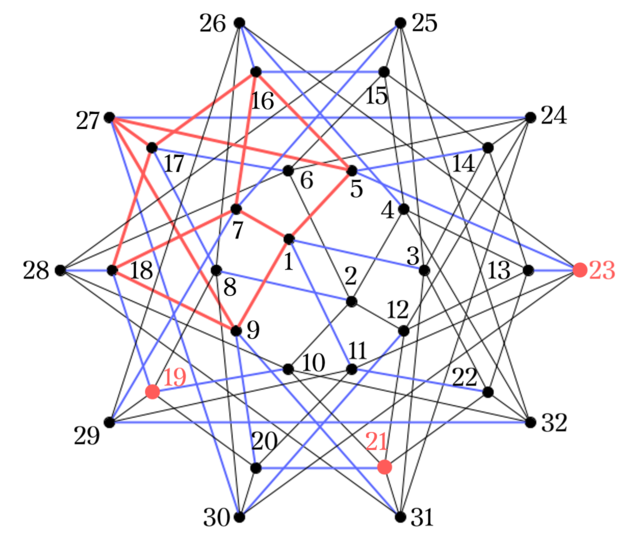
点$19$は青い辺によって$18$と$10$に接続されている. このうち, $18$は赤い辺の上にあるため, $19$を$18$へ移す. $23$も同様にして$5$へ移し, $21$に関しては$20\rightarrow9$と辿って$9$へ移す.

2.　赤の立方体から4つの候補を得る

　赤い辺の立方体を書き直すと,

となり$16$を得るが, $9,18,5$は青い辺を辿って見つけた数字であることを考慮する必要がある. よって, 候補は

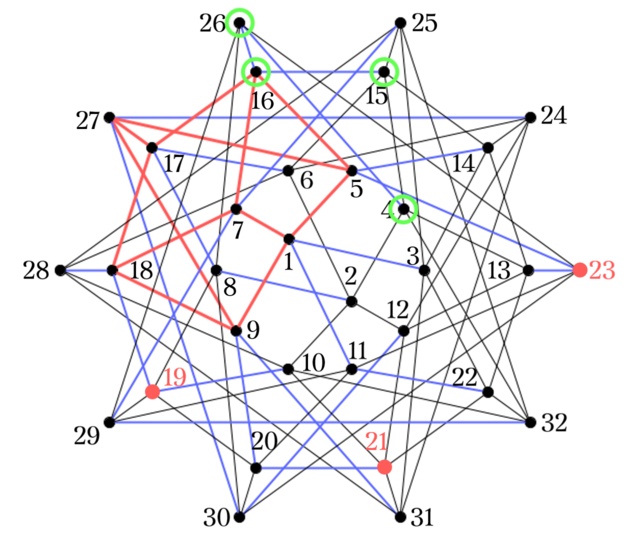
緑の円で囲んである$4,15,16,26$となる.

3.　2つのグラフの共通部分を取る

　上の操作を$C_2$でも行えば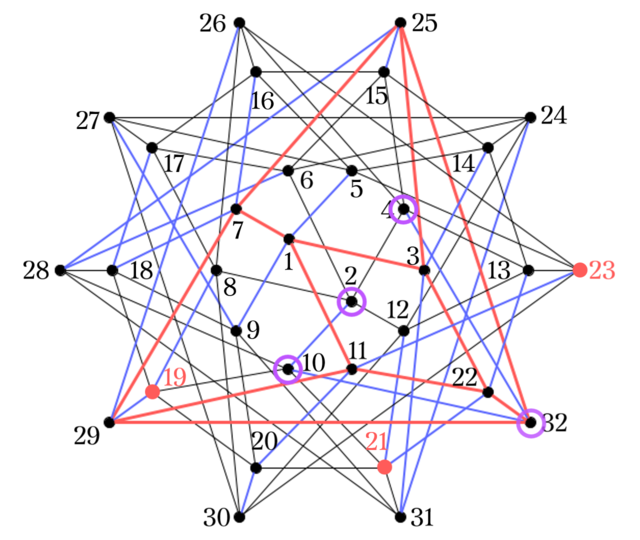

と, 候補$(2,4,10,32)$を得る.
2つの候補$(4,15,16,26),(2,4,10,32)$に共通する$4$を取って, $(4,19,21,23)$が確定した. 以上の流れをまとめたのが下のGIF.

青い辺上に2点以上ある場合

　例外パターンとして, $(3,19,28)$が挙げられ, $C_1$のグラフで候補を探すときに少し困ったことになる.

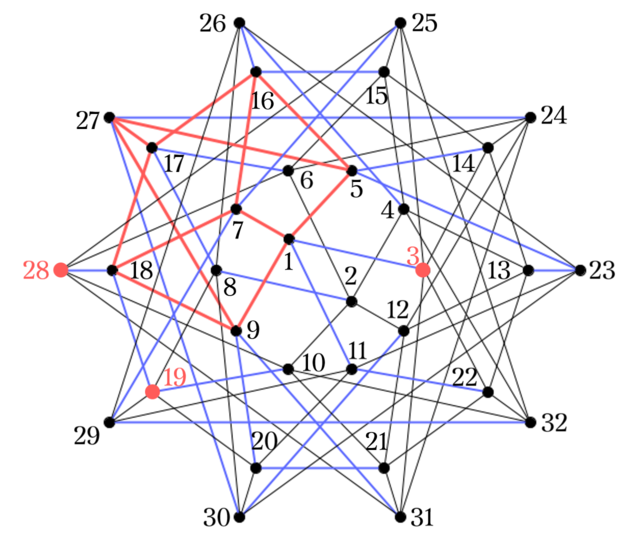
$19,28$が同じ青い辺上にあり, どちらも$18$に移ってしまう.
　ここで, 青い辺はすべて四角形をなしていることに着目する. 例えば, $10\rightarrow19\rightarrow18\rightarrow28$と辿ると, 必ず$28\rightarrow10$と戻れるような辺が存在している. $19,28$は互いに四角形の対角線上にあるため, $3$がある四角形で同じく対角線上にある$11$を選べば$(3,11,19,28)$が得られる.
　3点が同じ青い経路上にある場合は, 残りの点を取る. 例えば, $20,21,31$に対しては$9$を取り, $(9,20,21,31)$を得る.

原理

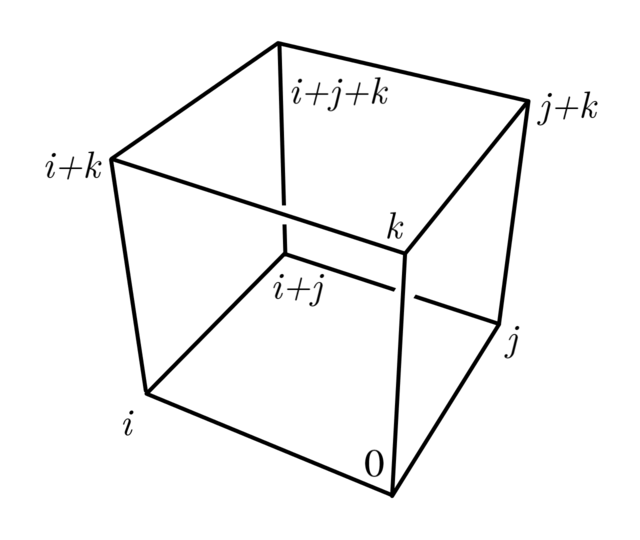
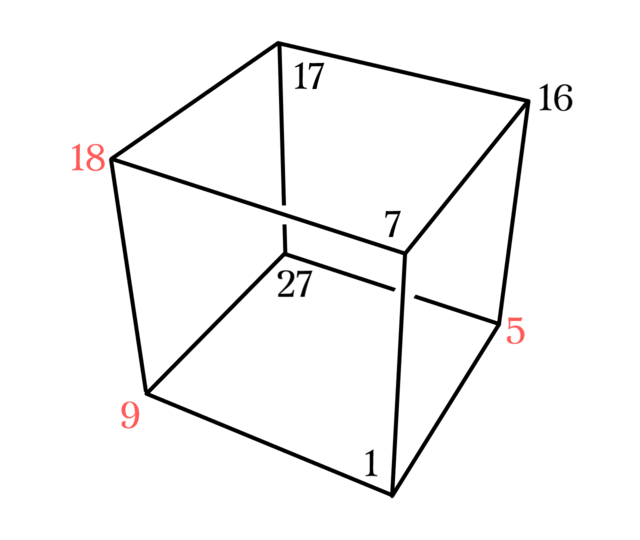
　この構成法は定理1を可視化したものになっていて, ${\mathbb{F}_2}^3$の標準基底を$i,j,k$とすると, $S_3$の3つ組からブロックを得る操作は, Fig12. のような立方体で平行四辺形を得る操作と捉えることができる.
　同様に${\mathbb{F}_2}^5$の標準基底$i,j,k,l,m$を$T_5$にプロットし, $i,j,k$が張る立方体を赤で彩色するとFig13. のようになる. 青い辺上の点を移動させる操作は, $l,m$の項を消して$i,j,k$の係数を確定させることを意味している. 上で扱った$(19,21,23)$は, Fig13. では$(i+j+l,j+l+m,k+l)$に対応していて, $i,j,k$の項のみ足し合わせると
\begin{eqnarray} (i+j)+j+k=i+k \end{eqnarray}
となり, $i+k+c_1l+c_2m\hspace{2mm}(c_1,c_2\in\mathbb{F}_2)$の4つが候補となる.

$C_2$は$i,l,m$が張る立方体で

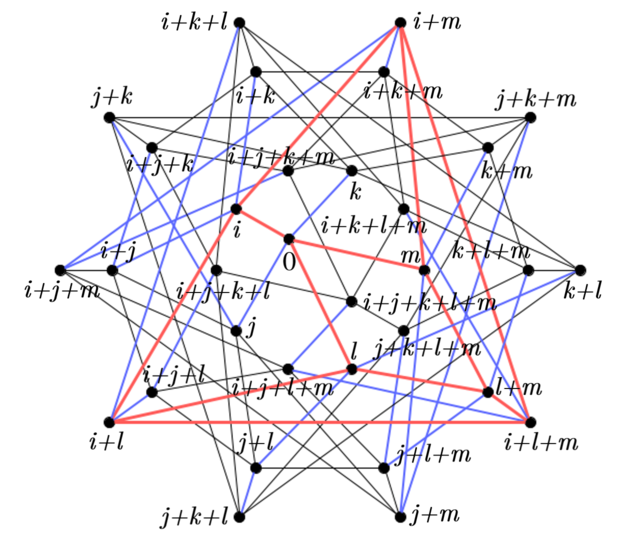
同様の操作によって$l,m$の係数を確定させる.
\begin{eqnarray} (i+l)+(l+m)+l=i+l+m \end{eqnarray}
から$i+c_3j+c_4k+l+m\hspace{2mm}(c_3,c_4\in\mathbb{F}_2)$が候補で, 先ほど得られた式と合わせて
\begin{eqnarray} i+k+c_1l+c_2m=i+c_3j+c_4k+l+m\\ c_1=1,c_2=1,c_3=0,c_4=1 \end{eqnarray}
となり, これが共通部分を求める操作と対応している.
式の上では
\begin{eqnarray} (i+j+l)+(j+l+m)+(k+l)=i+k+l+m \end{eqnarray}
と簡単に求まるが, この足し算を回りくどくすることで可視化をしている.