12次マシュー群1/3 - S(2,3,9)の性質
- フィッシャー不等式
- 算術三角形
- 自己同型群
- アフィン平面
-
シュタイナー三重系
- マシュー群 $M_{11}$と$M_{12}$
- S(2,3,9)の性質
- S(3,4,10)の構成
- $M_{11}$と$M_{12}$
- 射影平面
- シュタイナー四重系
本筋から逸れる証明は折畳んでいる場合があるが, クリックで開くことができる.
マシュー群
以下のように定義されるシュタイナーシステムの自己同型群をマシュー群と呼ぶ.
\begin{eqnarray}
M_{11}=\mathop{\rm Aut}S(4,5,11)\\
M_{12}=\mathop{\rm Aut}S(5,6,12)\\
M_{22}=\mathop{\rm Aut}S(3,6,22)\\
M_{23}=\mathop{\rm Aut}S(4,7,23)\\
M_{24}=\mathop{\rm Aut}S(5,8,24)\\
\end{eqnarray}
余談
クリックして開く
マシュー群は複雑さや応用上の理由から群論の入門書で本格的に扱われている姿を見れず, 発展的な立ち位置にあるという印象だが, 歴史的に見れば基礎的なSylowの定理よりも早い段階で発見されている. 大まかな年表は以下の通り.
1845年 コーシーの定理cauchy
$\hspace{3.8mm}$46年 Liouvilleによりガロア理論の原稿galoisが公開される
$\hspace{3.8mm}$61年 マシュー群$M_{11},M_{12}$mat61
$\hspace{3.8mm}$72年 シローの定理sylow
$\hspace{3.8mm}$73年 マシュー群$M_{22},M_{23},M_{24}$mat73
シローの定理は数十年の蓄積の結果であり, 年代の指標とするのはナンセンスかもしれないが, いずれにせよマシュー群が群論の黎明期に発見されたことは間違いない. 19世紀中頃の多重推移群としては, クロネッカーにより二重推移群が, エルミートにより三重推移群が研究されており, 四重・五重推移の群は未踏の領域であった. そのような中で, マシューはコーシーの回想録からヒントを得mat61, 鋭五重推移の$M_{12}$を構成することで有限群論を前進させた. さらに, mat61の274ページには$M_{24}$への示唆が確認でき, 1860年頃には既に5つのマシュー群の構想があったものと思われる. このことからもマシュー群は数年, 数十年を先取りしているような代物であることが窺えるが, 散在型有限単純群という視点からはその先駆性がより際立つ.
1861年 マシュー群$M_{11},M_{12}$
$\hspace{3.8mm}$73年 マシュー群$M_{22},M_{23},M_{24}$
1938年 $S(5,8,24)$の構成(ウィット)witt
$\hspace{3.8mm}$65年 散在型のジャンコー群$J_1$
$\hspace{3.8mm}$66年 $M_{24}$の指標表と$S(5,8,24)$の全ブロック列挙(トッド)
$\hspace{3.8mm}$76年 ミラクル・オクタッド・ジェネレーターを用いた$S(5,8,24)$の構成(カーティス)curtis
カーティスが構築した$S(5,8,24)$の構成法ミラクル・オクタッド・ジェネレーター (MOG)はジャンコー群$J_4$やモンスター$\mathbb{M}$の構成に必要不可欠でありwilson, マシュー群は有限群論の中心的な要素であり続けている.
$M_{11}$と$M_{12}$に関しては, \begin{eqnarray}S(5,6,12)=S(4+1,5+1,11+1)=S(2+3,3+3,9+3)
\end{eqnarray}
と, $S(2,3,9)$からの拡大で得られ, アーネスト・ウィットwittに因んで$S(4,5,11),S(5,6,12)$をそれぞれ$W_{11},W_{12}$と略記する.
$W_{11},W_{12}$を構成するためには$S(3,4,10)\eqqcolon W_{10}$を通らなければならないが, $W_{10}$はブロックとして$S(2,3,9)$の直線と四角形を持っており, 任意の三角形が必ずどこかの四角形に一度だけ含まれているという条件を満足している. そこで, $S(2,3,9)$の四角形や自己同型群など基本的な性質について調べることから始める.
以下, $S\coloneqq S(2,3,9)$とする.
$S$の四角形
証明(修正前)
同一直線上にない5点集合$F$を選べたと仮定すると, $F$の中の点を通る2直線の位置関係は, $F$の外で交差するか, $F$の中で交差するか, そうでなければ平行であるかの3通りであり, どの場合でも$F$の外に1つ以上の点がなければならない.
即ち, $F$の中の点を通る2直線を決めれば, $F$の外にある点が1つ以上定まり, $F$の中から2直線を選ぶ方法は少なくとも$\mqty(5\\4)=5$通りあるため, $F$の外には5つ以上の点が存在することになるが, $S$は9点集合であるため矛盾.
したがって, $S$の任意の5点は少なくとも1本の直線に含まれる.
5点集合を$F=\lbrace\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5\rbrace$とする.
$S$の2点を選べば一意にそれらを含む直線が決まることから, $(\alpha_i,\alpha_j)$が含まれる直線を$(\alpha_i,\alpha_j,\alpha_{i\circ j})$と表記する. ここで, $i,j,k$がすべて異なれば, 同じ2点が複数の直線に含まれることはあり得ないため, $\alpha_{i\circ j},\alpha_{j\circ k},\alpha_{k\circ i}$はすべて異なる. このことを$F$に適用することで矛盾を導く.
$\alpha_{1\circ i}\hspace{2mm}(i=2,3,4,5)$はすべて異なり, 仮定からすべて$F$の外にある. $S$は9点集合であったから, $\alpha_1,\alpha_i,\alpha_{1\circ i}$で$S$の点は言い尽くされている.
$\alpha_{2\circ j}\hspace{2mm}(j=3,4,5)$についてもすべて異なり, $j$に対して$\alpha_{2\circ j}=\alpha_{1\circ k}\hspace{2mm}(k=3,4,5,j\neq k)$なる$k$を取ることができる.
このとき, $\alpha_{3\circ4}=\alpha_{1\circ 2}$が決まる.
なぜなら, $\alpha_{3\circ4}$は$\alpha_{1\circ3},\alpha_{1\circ4}$と異なり, $\alpha_{1\circ5}=\alpha_{2\circ3}$または$\alpha_{1\circ5}=\alpha_{2\circ4}$であるから, いずれにせよ$\alpha_{3\circ4}\neq\alpha_{1\circ5}$.
同様に$\alpha_{3\circ5}=\alpha_{1\circ 2}$が成り立つが, これは$\alpha_{3\circ4}\neq\alpha_{3\circ5}$に矛盾.
したがって, $\alpha_{1\circ i}$のいずれかは$F$の中にいなければいけない.
添数は任意だったため, $S$のすべての5点集合について同様のことが示せる.
証明
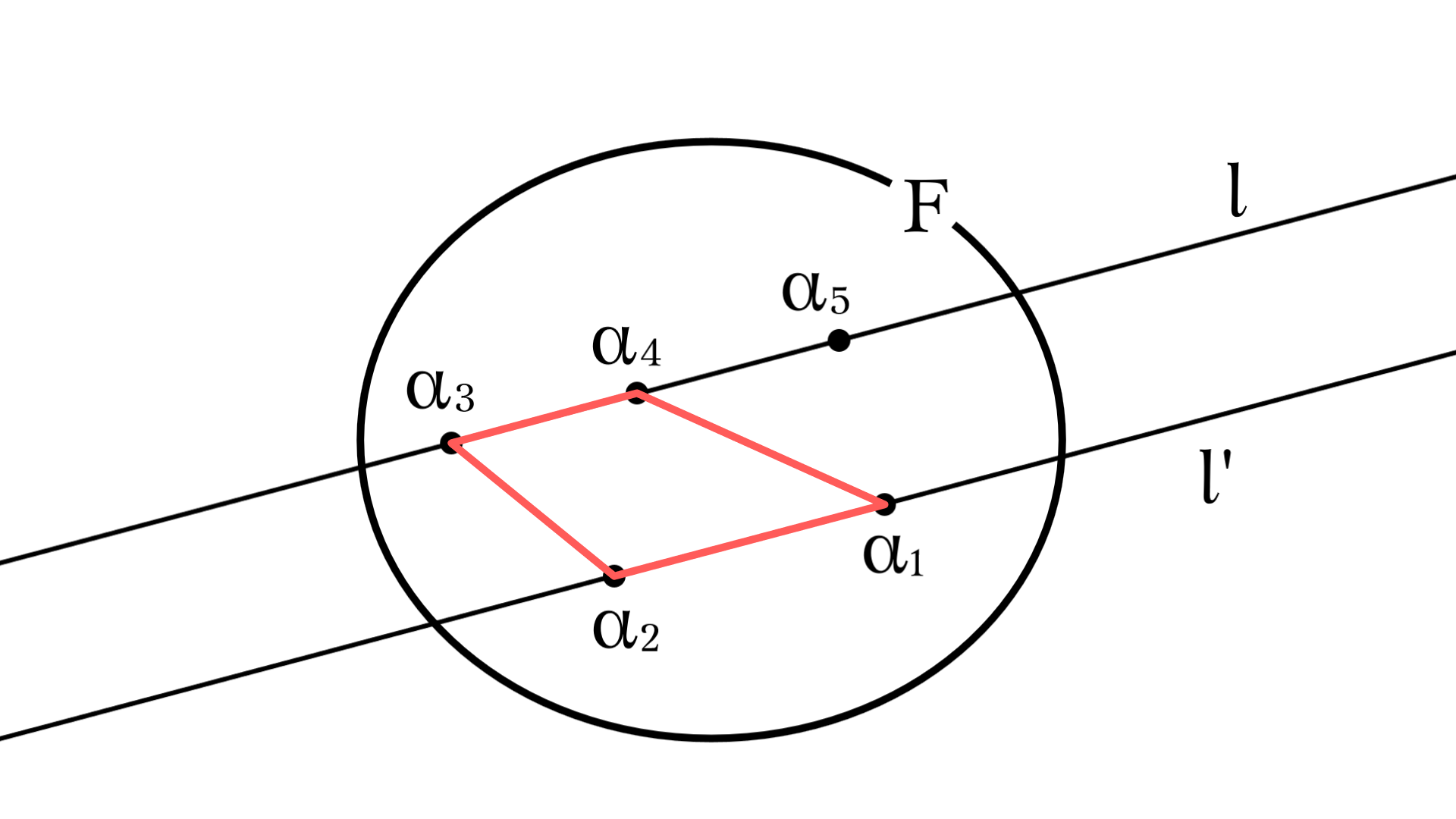
$S$の5点集合を$F=\lbrace\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5\rbrace$とする.
補題1から同一直線上にある点が存在して, それを$l=\lbrace\alpha_3,\alpha_4,\alpha_5\rbrace$としても一般性を失わない.
アフィン平面の同値な条件
から$l$に対して$\alpha_2$を選ぶと$l$と共通部分を持たず, $\alpha_2$を通る直線が一意に定まり, これを$l'$とする.
残りの$\alpha_1$がどこに位置していたとしても四角形が存在することを示す.
まず$\alpha_1$は$l$上にはない.
$l'$上にあったとすると, $l$上の任意の2点と$\alpha_1,\alpha_2$で四角形が作れる.
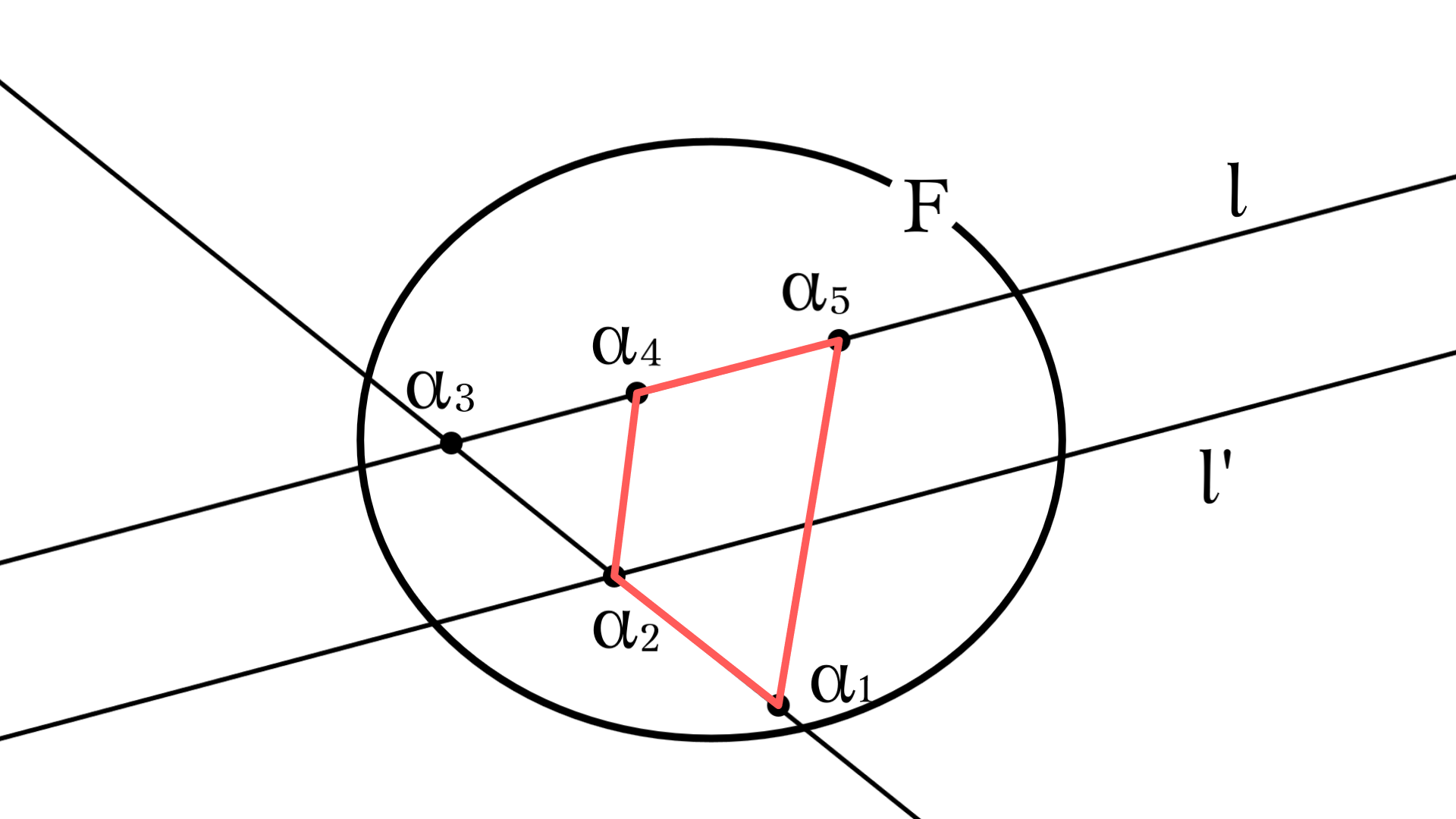
直線$(\alpha_1,\alpha_2,\alpha_3)$が存在していたとすると, $(\alpha_1,\alpha_2,\alpha_4,\alpha_5)$で四角形が作れる.
これは$(\alpha_1,\alpha_2,\alpha_4)$も$(\alpha_1,\alpha_2,\alpha_5)$のときも同様である.
$\alpha_1$が上のどの場合にも当てはまらないとき, $F$の点で同一直線上にあるのは$(\alpha_3,\alpha_4,\alpha_5)$のみであるから, $l$の任意の2点と$\alpha_1,\alpha_2$で四角形が作れる.
平行類への作用
証明
(${\rm Aut}S$が平行類に作用すること)
$\sigma\in{\rm Aut}S,l_1,l_2\in S$とすると
\begin{eqnarray}
\sigma(l_1\cap l_2)=\sigma l_1\cap\sigma l_2
\end{eqnarray}
であるから, $l_1,l_2$が平行であることと$\sigma l_1,\sigma l_2$が平行であることが同値である.
よって, $\sigma$は平行類の置換を引き起こす.
(作用が$\mathfrak{S}_4$であること)
\begin{eqnarray}
S=\lbrace(1,2,9),(3,4,5),(6,7,8),(1,3,8),\\
(2,4,6),(5,7,9),(1,4,7),(2,5,8),\\
(3,6,9),(1,5,6),(2,3,7),(4,8,9)\rbrace
\end{eqnarray}
として,平行類を
\begin{eqnarray}
A=\lbrace(1,2,9),(3,4,5),(6,7,8)\rbrace\\
B=\lbrace(1,3,8),(2,4,6),(5,7,9)\rbrace\\
C=\lbrace(1,4,7),(2,5,8),(3,6,9)\rbrace\\
D=\lbrace(1,5,6),(2,3,7),(4,8,9)\rbrace
\end{eqnarray}
とおく. 対称群は隣接互換から生成されるのだから$\mqty(A&B),\mqty(B&C),\mqty(C&D)$という置換を見つければ十分である.
実際,$\mqty(1&5)\mqty(2&7)\mqty(4&8)\in{\rm Aut}S$は$\mqty(A&B)$を,
$\mqty(2&9)\mqty(3&4)\mqty(7&8)$は$\mqty(B&C)$を,
$\mqty(1&3)\mqty(2&4)\mqty(5&9)$は$\mqty(C&D)$を引き起こすため, ${\rm Aut}S$は$S$の平行類に$\mathfrak{S}_4$として作用する.
証明中に登場した3つの置換はすべてアフィン平面を反転させる操作を表している.

$S$の一意性
これまで$S$の構成法として, $K_9$の辺彩色 , STSの直積 , ラテン方格を用いた方法 の3種類を扱ってきたが, 実のところ生成されたシステムはすべて同じ構造を持っている. このようなことから, シュタイナーシステムも群などと同様, ある構造に従う無限系列であることが見え隠れしていて, 実際「システム」よりも「族」という語が適切との指摘もあるhanani.
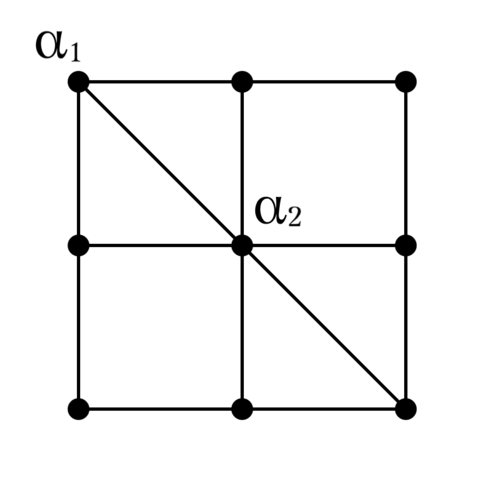
任意の$S$に対して, 以下に示すような操作が可能である.
アフィン平面-定理2
より, $S$について, 3つの直線を含んだ4つの平行類が得られ, その中の2つを$R,C$とする.
$R,C$から直線$B_R,B_C$をそれぞれ取ると,
$|B_R\cap B_C|=1$
.
$R=\lbrace B_{R1},B_{R2},B_{R3}\rbrace, C=\lbrace B_{C1},B_{C2},B_{C3}\rbrace$とおき, その交点を$|B_{R1}\cap B_{C1}|=\alpha_1,|B_{R2}\cap B_{C2}|=\alpha_2$とすると, この2点を含む直線$B=\lbrace\alpha_1,\alpha_2,\alpha_3\rbrace$と点$\alpha_3$が存在する.
このとき, $\alpha_3\in B_{R1}$とすると, $\alpha_1,\alpha_3\in B_{R1}$であるから, $B=B_{R1}$となるが, $\alpha_2\notin B_{R1}$より矛盾.
同様に$\alpha_3\in B_{R2},B_{C1},B_{C2}$とすると矛盾するため, $\alpha_3\notin B_{R1},B_{R2},B_{C1},B_{C2}$.
アフィン平面の同値な条件
から, $\alpha_3$は$B_{R1},B_{R2},B_{R3}$のいずれかに含まれていなければならない.
したがって, $\alpha_3\in B_{R3}$.
同様にして, $\alpha_3\in B_{C3}$.
$B_{R1}\cap B_{C1},B_{R2}\cap B_{C3}$, $B_{R1}\cap B_{C2},B_{R2}\cap B_{C1}$, $B_{R1}\cap B_{C2},B_{R2}\cap B_{C3}$, $B_{R1}\cap B_{C3},B_{R2}\cap B_{C1}$, $B_{R1}\cap B_{C3},B_{R2}\cap B_{C2}$の5つについても上記の操作を行えば, すべて合わせて12本の直線が得られ, $S$のブロックを網羅できる.
与えられた2つの異なる$S$に対して, この操作を行い, 点と点, ブロックとブロックを対応させれば同型が得られる.
$S$と${\mathbb{F}_3}^2$
$S$はSTSの直積を用いて
\begin{eqnarray}S={\rm STS}(9)={\rm STS}(3)\times{\rm STS}(3)\end{eqnarray}
と表せ, ブロックを下図のように直線として表現できるのだった.
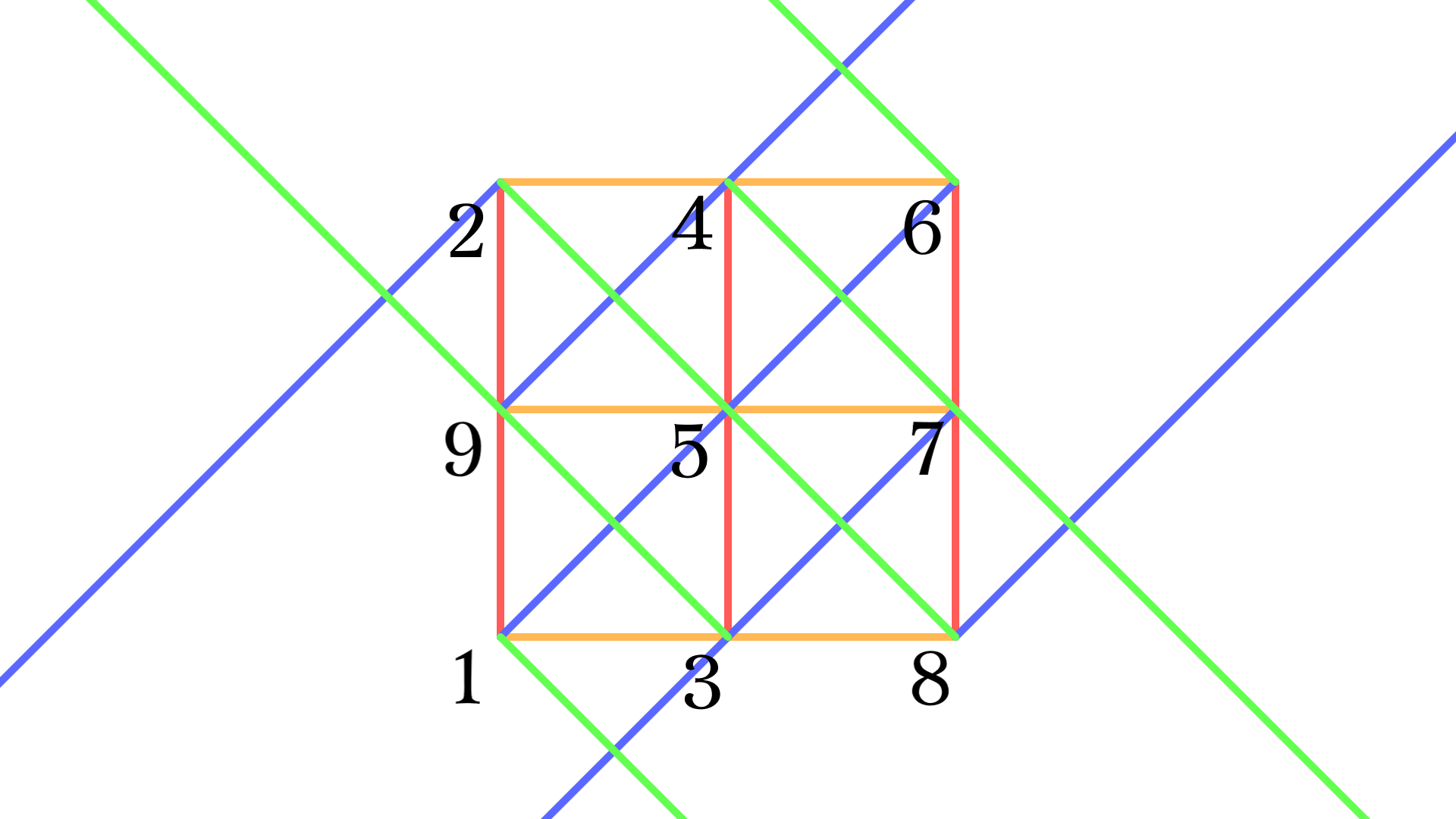
これは次のように上下左右に循環したトーラスとしても描ける.
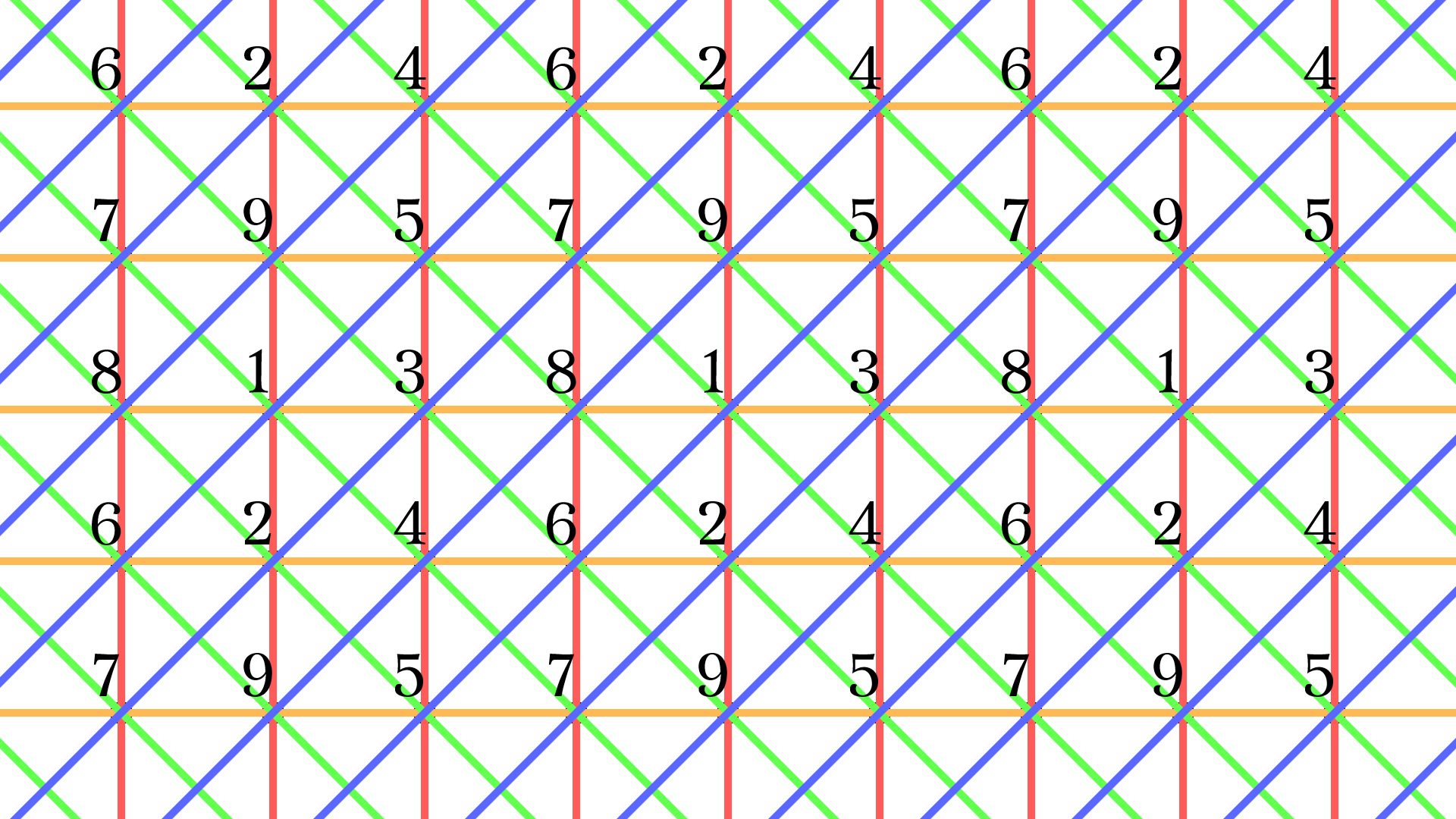
Fig3. を$\mathbb{F}_3$上の線型空間と見做す. 原点を1とすると, 任意のベクトル$v\in{\mathbb{F}_3}^2$は$S$の直線と対応付けができる. ${\mathbb{F}_3}^2$のベクトルは8つしかないので列挙してみると
\begin{eqnarray}
\mqty[1\\3]\mapsto(1,3,8)\hspace{3mm}\mqty[1\\5]\mapsto(1,5,6)\hspace{3mm}\mqty[1\\9]\mapsto(1,2,9)\hspace{3mm}\mqty[1\\7]\mapsto(1,4,7)\\
\mqty[1\\8]\mapsto(1,3,8)\hspace{3mm}\mqty[1\\6]\mapsto(1,5,6)\hspace{3mm}\mqty[1\\2]\mapsto(1,2,9)\hspace{3mm}\mqty[1\\4]\mapsto(1,4,7)
\end{eqnarray}
が得られる. $S$の自己同型群は, $S$の直線を直線に移すような写像全体であり, これは${\mathbb{F}_3}^2$のベクトルをベクトルに移す一般線型群$GL_2(\mathbb{F}_3)$と同じ構造を持つことが分かる. さらに, 原点を1に固定する必要はないため, そこへ平行移動を加えたアフィン群
\begin{eqnarray}
{\rm AGL}_2(\mathbb{F}_3)=\lbrace t_{a,v}|t_{a,v}(u)=au+v,a\in{\rm GL}_2(\mathbb{F}_3),u,v\in{\mathbb{F}_3}^2\rbrace
\end{eqnarray}
が$S$の対称性を表している.
$\mathbb{F}_3=\lbrace0,1,2\rbrace$, $\Omega_1,\Omega_2$を$\mathbb{F}_3$によって添え字付けられた集合とし, それぞれの元を$\Omega_1=\lbrace\alpha_0,\alpha_1,\alpha_2\rbrace,\Omega_2=\lbrace\beta_0,\beta_1,\beta_2\rbrace$とする.
定理4から$S$はすべて${\rm STS}(3)\times{\rm STS}(3)$と同型であり, ${\rm STS}(\Omega_1)\times{\rm STS}(\Omega_2)$
\begin{eqnarray}\left\{\begin{array}{ll}
((\alpha_0,\beta_r),(\alpha_1,\beta_r),(\alpha_2,\beta_r)) & \beta_r\in\Omega_2\\
((\alpha_i,\beta_0),(\alpha_i,\beta_1),(\alpha_i,\beta_2)) & \alpha_i\in\Omega_1\\
((\alpha_0,\beta_r),(\alpha_1,\beta_s),(\alpha_2,\beta_t)) & \beta_r,\beta_s,\beta_t\in\Omega_2
\end{array}\right.\end{eqnarray}
に$S$を代表させても一般性を失わない.
${\mathbb{F}_3}^2$の基底$\mqty[1\\0],\mqty[0\\1]\in{\mathbb{F}_3}^2$をそれぞれ$(\alpha_1,\beta_0),(\alpha_0,\beta_1)\in\Omega_1\times\Omega_2$へ送れば, ${\mathbb{F}_3}^2$のベクトルと$\Omega_1\times\Omega_2$の元が一対一に対応する. よって, $t\in{\rm AGL}_2(\mathbb{F}_3)$は$\alpha,\beta$の添え字を動かすが, ${\rm STS}(\Omega_1)\times{\rm STS}(\Omega_2)$の構成では$\alpha$か$\beta$の添え字が固定されているため, $t$は${\rm STS}(\Omega_1)\times{\rm STS}(\Omega_2)$のブロックをブロックへ移す.
基底が対応しているため, ${\rm AGL}_2(\mathbb{F}_3)\longrightarrow{\rm Aut}S$は全単射であり, ${\rm AGL}_2(\mathbb{F}_3)\cong{\rm Aut}S$
要するに, ${\mathbb{F}_3}^2$と${\rm STS}(3)\times{\rm STS}(3)$が等価であるため, その写像も等価ということである.
正則であることと行列式が0でないことは同値である.
ある列の成分がすべて0である行列の行列式は0であるから, 1列目の選び方は$p^n-1$通り.
2列目が1列目の定数倍であれば, 列基本変形で2列目の成分をすべて0にできてしまうため, 2列目には, 1列目の線型結合ではない, という制約が加わる. よって2列目の選び方は$p^n-p$通り.
以下同様に列を選んでいくと, 正則な行列の個数は$\prod_{i=0}^{n-1}(p^n-p^i)$となる.
詳細については, yukie青雪江p. 130-131, suz鈴木p. 77-78などを参照されたい.
補題6から$\#{\rm GL}_2(\mathbb{F}_3)=(9-1)(9-3)=48$.
原点を含め9つの平行移動があるため, $\#{\rm Aut}S=9\cdot48=432$
