【ストリング図で学ぶ圏論 #6】モナドの例

はじめに

前回の記事 では，モナドについて説明しました。ここでは，モナドの具体例として，計算機科学でしばしば登場する「リストモナド」と「状態モナド」について，図式を用いて紹介します。

本連載の目次

#1： 圏の定義と具体例
#2： 関手と自然変換
#3： 垂直合成と水平合成
#4： モノイダル圏
#5： モナドとは自己関手の圏におけるモノイド対象のこと
#6： モナドの例（この記事）
#7： 随伴
#8： 関手を表す線の順序の交換
#9： 普遍射と随伴・極限・カン拡張
#10： ホム関手のストリング図（前編）
#11： ホム関手のストリング図（後編）
#12： 米田の補題
番外編1： 視覚的に理解するクライスリトリプルとモナドの同値性
番外編2： 線形代数の圏論的な性質（？）を圏論なしで説明する

準備：バインド演算

Haskellなどの関数型プログラミング言語では，>>= のようなバインド演算がよく用いられます。この演算は各$a,b\in \mathcal{C}$について実質的にホムセット$\mathcal{C}(a,Tb)$からホムセット$\mathcal{C}(Ta,Tb)$への写像を表しており，この写像は積$\mu$を用いて次式のように定まります。

バインド演算による写像$f\mapsto {\mu }_b\circ Tf$

この写像を暫定的に持ち上げとよぶことにして，各$f\in \mathcal{C}(a,Tb)$に対して$f^{\mathrm{\#}}:={\mu }_b\circ Tf\in \mathcal{C}(Ta,Tb)$とおきます。

リストモナド

リストモナドの定義

まず，リストモナド$⟨L,\mu ,\eta ⟩$（ただし$L:\mathbf{Set}\to \mathbf{Set}$）の定義を述べるため，関手$L$と積$\mu$と単位元$\eta$のそれぞれを定めます。

関手$L$

関手$L:\mathbf{Set}\to \mathbf{Set}$は，各集合$X\in \mathbf{Set}$を集合$LX\in \mathbf{Set}$に写すものとします。ただし，$LX$は$⟨x_i{⟩}_{i=1}^n$ $(n\in \mathbb{N},x_1,\dots ,x_n\in X)$の形で表されるもの（つまり$X$の要素からなる有限長のリスト）をすべて集めた集合です。これにより，$L$の対象への作用が定まります。以降では，$⟨x_i{⟩}_{i=1}^n$をしばしば簡略化して$⟨x_i{⟩}_i$のように書きます。$LX$の各要素$⟨x_i{⟩}_i$は次式のように表せます。

$⟨x_i{⟩}_i\in LX$
$$\begin{array}{}\text{(1)}& \end{array}$$

また，$L$は各写像$f\in \mathbf{Set}(X,Y)$を写像$Lf\in \mathbf{Set}(LX,LY)$に写します。この写像$Lf$を，「各$⟨x_i{⟩}_i\in LX$を$⟨f(x_i){⟩}_i\in LY$に写すもの」として定めます。つまり，次の図式を満たすものとします。

式$Lf(⟨x_i{⟩}_i)=⟨f(x_i){⟩}_i$

これにより，$L$の射への作用が定まります。

積$\mu$

積（自然変換）$\mu :L\bullet L\Rightarrow L$の各成分${\mu }_X$$(X\in \mathbf{Set})$は，集合$(L\bullet L)X$から集合$LX$への写像です。この写像${\mu }_X$を

$${\mu }_X:(L\bullet L)X\ni ⟨⟨x_{i,j}{⟩}_i{⟩}_j\mapsto ⟨x_{i,j}{⟩}_{i,j}\in LX$$

と定めます。${\mu }_X$は次の図式で表されます。
式${\mu }_X(⟨⟨x_{i,j}{⟩}_i{⟩}_j)=⟨x_{i,j}{⟩}_{(i,j)}$
大ざっぱに述べると，各${\mu }_X$は2重のリストを1重のリストに写すような働きをします。

単位元$\eta$

単位元（自然変換）$\eta :1_{\mathbf{Set}}\Rightarrow L$の各成分${\eta }_X$$(X\in \mathbf{Set})$は，集合$X$から集合$LX$への写像です。この写像${\eta }_X$を

$${\eta }_X:X\ni x\mapsto ⟨x⟩\in LX$$

と定めます。${\eta }_X$は次の図式で表されます。

式${\eta }_X(x)=⟨x⟩$
各${\eta }_X$は，$X$の各要素$x$を1個の要素のみからなるリスト$⟨x⟩$に写します。

リストモナドがモナドであることの確認

リストモナドがモナドである，つまり結合律と単位律を満たすことを確認しておきます。

結合律

結合律を満たすことは，各$⟨⟨⟨x_{i,j,k}{⟩}_i{⟩}_j{⟩}_k\in (T\bullet T\bullet T)X$に対して次式が成り立つことからわかります。

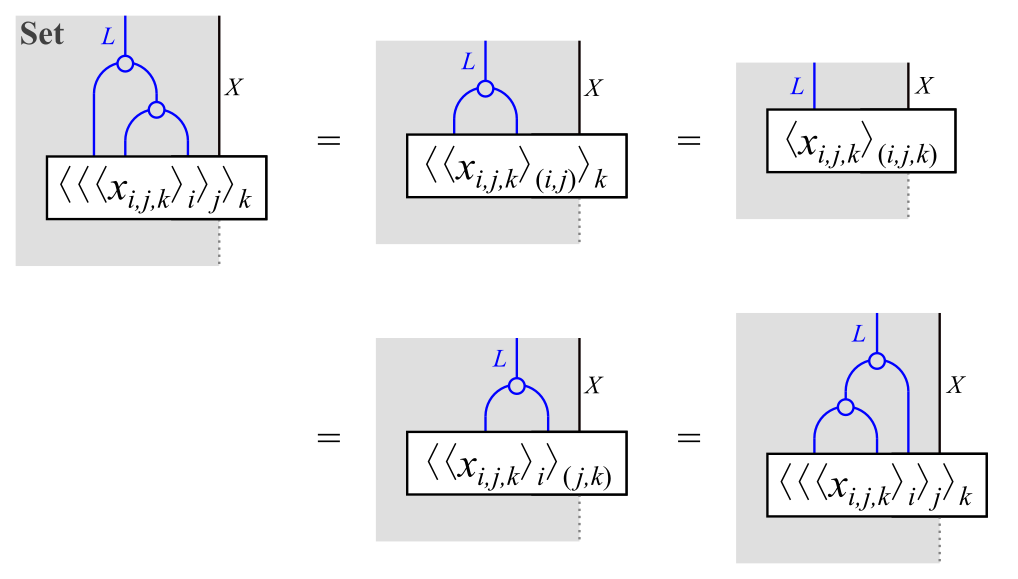結合律

単位律

単位律を満たすことは，各$⟨x_i{⟩}_i\in TX$に対して次式が成り立つことからわかります。
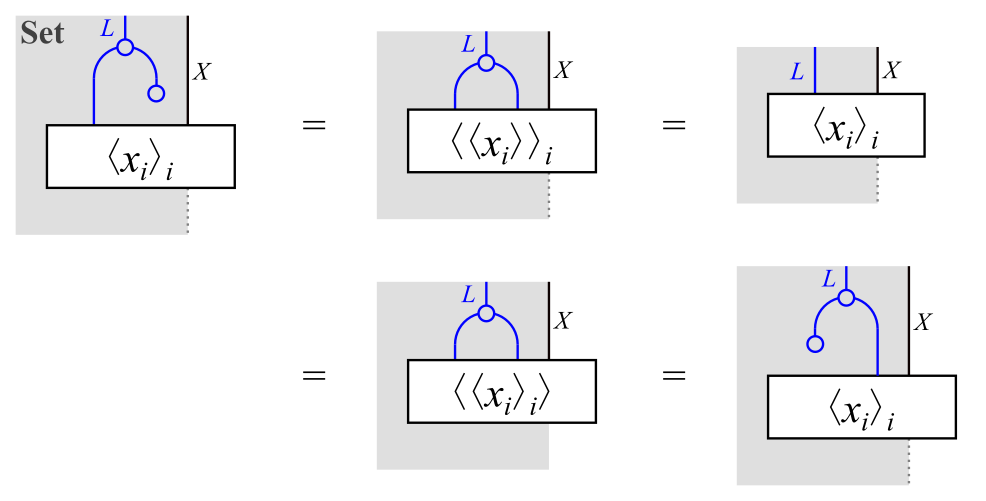単位律

持ち上げ

持ち上げ$\mathbf{Set}(X,LY)\ni f\mapsto f^{\mathrm{\#}}\in \mathbf{Set}(LX,LY)$を考えます。$f^{\mathrm{\#}}$に各$⟨x_i{⟩}_i\in LX$を入力したときの出力は次式で表されます。

$f^{\mathrm{\#}}(⟨x_i{⟩}_i)$

なお，各$f(x_i)$は$TY$の要素（つまりリスト）です。このため，$⟨f(x_i){⟩}_i$は$(T\bullet T)X$の要素（つまりリストのリスト）です。

状態モナド

状態モナドの定義

状態モナド$⟨T,\mu ,\eta ⟩$（ただし$T:\mathbf{Set}\to \mathbf{Set}$）の定義を述べます。

関手$T$

以降では，各集合$X,Y$について$\mathbf{Set}(X,Y)$を$Y^X$と書くことにします。集合$S$を任意に選んで固定して，$S$の要素を状態とよぶことにします。このとき，関手$T:\mathbf{Set}\to \mathbf{Set}$は，各集合$X\in \mathbf{Set}$を集合$TX:=(X\times S{)}^S$に写すものとします。これにより，$T$の対象への作用が定まります。

集合$TX=(X\times S{)}^S$の各要素$a$は，$S$から$X\times S$への写像です。つまり，$a$は各状態$s\in S$を$X$の要素$x(s)$と状態$t(s)$の組$⟨x(s),t(s)⟩\in X\times S$に写します（$⟨x,t⟩$と書く代わりに，これらが$s$に依存することを表すために$⟨x(s),t(s)⟩$と書きました）。$TX$を次の図式で表すことにします。

集合$TX$

左辺と右辺は同じ$TX$を2通りの方法で表したものです。なお，上付き文字${}^S$を表す線$S$を下向きの矢印として表しています。また，この矢印と$X\times S$を表す2本の線$X$と$S$の間の境界を，念のため濃いグレーにより強調しています。このとき，$a\in TX$は次式のように表されます。

$a\in TX$の2通りの表記

また，$T$は各写像$f\in \mathbf{Set}(X,Y)$を写像$Tf\in \mathbf{Set}(TX,TY)=\mathbf{Set}((X\times S{)}^S,(Y\times S{)}^S)$に写します。この写像$Tf$を，「各写像$h:S\to X\times S$を写像$⟨f,1_S⟩\circ h:S\to Y\times S$に写すもの」として定めます。これにより，$T$の射への作用が定まります。写像$h\mapsto Tf(h)$は次の図式で表されます。

写像$h\mapsto Tf(h):=⟨f,1_S⟩\circ h$

このため，$Tf$は次式のように表されます。
$Tf$の2通りの表記
左辺と右辺は同じ$f$を2通りの方法で表したものです。

積$\mu$

積（自然変換）$\mu :T\bullet T\Rightarrow T$の各成分${\mu }_X$$(X\in \mathbf{Set})$は，集合$(T\bullet T)X$から集合$TX$への写像です。写像${\mu }_X$を$(T\bullet T)X=((X\times S{)}^S\times S{)}^S$の各要素，つまり$S\ni s\mapsto ⟨\xi (s),t(s)⟩\in (X\times S{)}^S\times S$の形の写像を$TX=(X\times S{)}^S$の要素である写像$S\ni s\mapsto \xi (s)(t(s))\in X\times S$に写すものとして定めます。大ざっぱに述べると，${\mu }_X$は写像$\xi (s):S\to X\times S$に状態$t(s)\in S$を入力するような働きをします。

写像
$${\epsilon }_X:X^S\times S\ni ⟨h,s⟩\mapsto h(s)\in X$$
を次の図式で表すことにします。

写像${\epsilon }_X$

このとき，${\epsilon }_X(h,s)=h(s)$は次式のように表せます。

式${\epsilon }_X(h,s)=h(s)$

直観的には，この左辺は写像$h$に$s$を入力することを表しているとみなせます。$\xi (s)(t(s))={\epsilon }_{X\times S}(\xi (s),t(s))$を用いると，写像${\mu }_X$は次の図式で表されることがわかります。

${\mu }_X$の2通りの表記

この右辺が，上で述べた${\mu }_X$の具体的な定義を図式で表したものです。

単位元$\eta$

単位元（自然変換）$\eta :1_{\mathbf{Set}}\Rightarrow T$の各成分${\eta }_X$$(X\in \mathbf{Set})$は，集合$X$から集合$TX$への写像です。この写像${\eta }_X$は，各$x\in X$を$TX=(X\times S{)}^S$の要素である写像$S\ni s\mapsto ⟨x,s⟩\in X\times S$に写すものとします。${\eta }_X$を次の図式で表すことにします。

${\eta }_X(x)$の2通りの表記

各${\eta }_X$は，集合$X$と集合$S$に対してともに「何もしない」（つまり恒等写像を施す）ような写像です。右辺では，恒等写像$1_S$を表す線$S$を180度曲げたかのような表記をしています。

状態モナドがモナドであることの確認

状態モナドがモナドである，つまり結合律と単位律を満たすことを確認しておきます。ここでは概要のみを説明します。

結合律

各集合$X$に対して次式が成り立ちます（このことは，$\{{\epsilon }_X{\}}_{X\in \mathbf{Set}}$が自然変換であることがわかれば，すぐにわかります）。

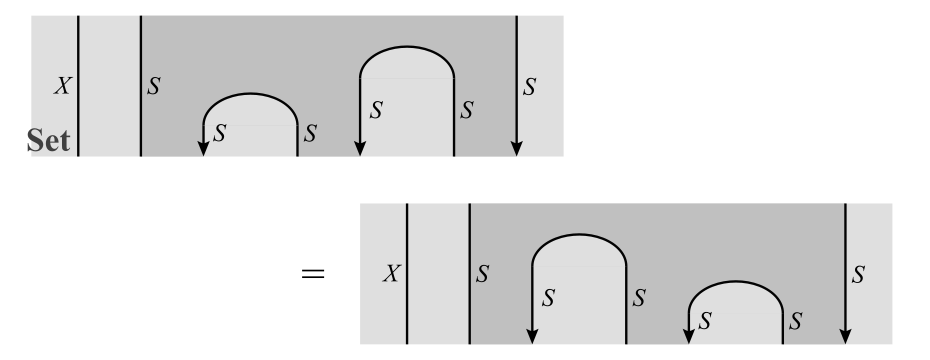結合律

これは，$(\mu \circ (1_T\bullet \mu ))X=(\mu \circ (\mu \bullet 1_T))X$を表しています。このため，結合律$\mu \circ (1_T\bullet \mu )=\mu \circ (\mu \bullet 1_T)$が成り立ちます。

単位律

各集合$X$に対して次式が成り立ちます。

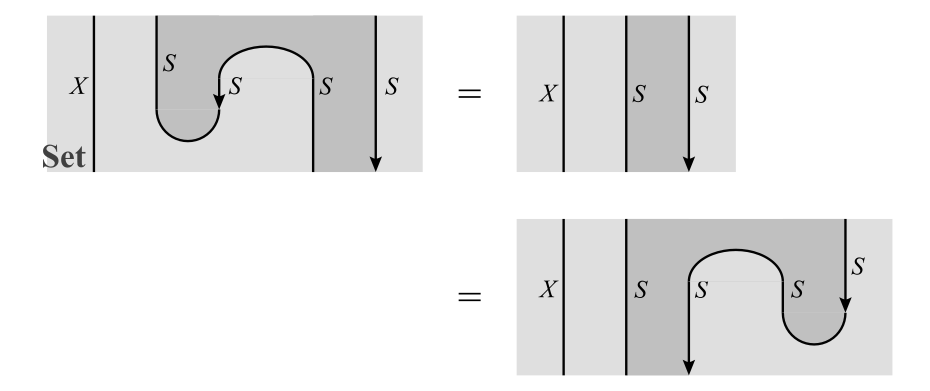単位律

このことは，直観的には「くねくねと曲がった線$S$をまっすぐに伸ばしても値は変わらない」と考えると，何となく納得できるかもしれません（随伴の知識があるとすぐに理解できるようになります）。この式は，$(\mu \circ (1_T\otimes \eta ))X=(1_T)X=(\mu \circ (\eta \bullet 1_T))X$を表しています。このため，単位律$\mu \circ (1_T\otimes \eta )=1_T=\mu \circ (\eta \bullet 1_T)$が成り立ちます。

持ち上げ

持ち上げ$\mathbf{Set}(X,TY)\ni f\mapsto f^{\mathrm{\#}}\in \mathbf{Set}(TX,TY)$を考えます。$f^{\mathrm{\#}}$は次式で表されます。

$f^{\mathrm{\#}}$

まとめ

リストモナドと状態モナドを，図式を用いて説明しました。詳しい説明は省略しましたが，図式に慣れればきっとこれらのモナドを視覚的にわかりやすく理解できることと思います。