【ストリング図で学ぶ圏論 #5】モナドとは自己関手の圏におけるモノイド対象のこと
はじめに
モナドは計算機科学や物理学などの分野でしばしば登場するため，その名前を聞いたことのある人は多いかもしれません。モノイドを一般化したモノイド対象という概念があり，モノイド対象の特別な場合としてモナドが定義できます。この記事では，モナドの定義として，モノイド対象に基づいた定義とより直接的な定義の2通りの方法を紹介します。
本連載の目次
#1：
圏の定義と具体例
#2：
関手と自然変換
#3：
垂直合成と水平合成
#4：
モノイダル圏
#5： モナドとは自己関手の圏におけるモノイド対象のこと（この記事）
#6：
モナドの例
#7：
随伴
モノイド
まず， 第1回の記事 で紹介したモノイドの定義を改めて明記します。
集合$\cM$と写像$\cM \times \cM \ni \braket{x,y} \mapsto xy \in \cM$（積とよぶ）と$1 \in \cM$（単位元とよぶ）の組$\braket{\cM,\cdot,1}$が次の二つの条件を満たすとき，モノイドとよぶ。
(1)結合律：$x(yz) = (xy)z \quad(\forall x,y,z \in \cM)$
(2)単位律：$x1 = x = 1x \quad (\forall x \in \cM)$
結合律
結合律は次の図式で表せます（$x,y,z \in \cM$は任意）。
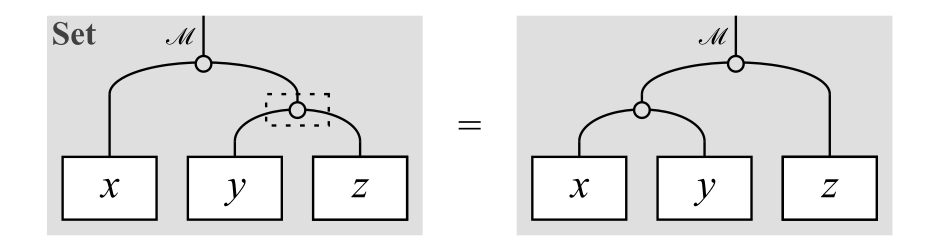結合律
$$\tag{1}\label{eq:1}$$
ただし，補助線（破線）で囲まれた丸は積$\cdot$を表しており，線はすべて集合$\cM$を表しています（線のラベル「$\cM$」は適宜省略しています）。この左辺は$x(yz)$を表しており，右辺は$(xy)z$を表しています。便宜上，積$\cdot$を$\mu$と書くことにすると，この式は次式と同値です。
(1)結合律：$\mu \c (1_\cM \times \mu) = \mu \c (\mu \times 1_\cM)$
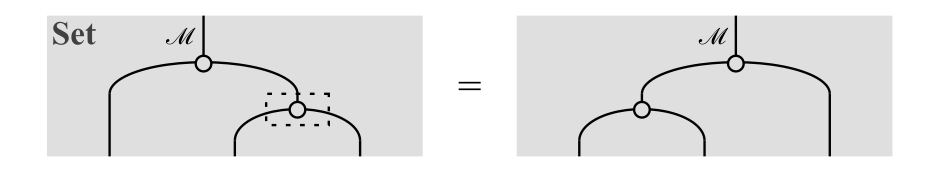結合律（別表現）
$$\tag{2}\label{eq:2}$$
ただし，恒等写像$1_\cM$は図式では単なる線として表しています。
$$ \cM \times \cM \times \cM \ni \braket{x,y,z} \xmapsto{1_\cM \times \mu} \braket{x,yz} \xmapsto{\mu} x(yz) \in \cM $$
ですので，$\braket{x,y,z}$を$x(yz)$に写します。同様に，右辺$\mu \c (\mu \times 1_\cM)$は写像
$$ \cM \times \cM \times \cM \ni \braket{x,y,z} \xmapsto{\mu \times 1_\cM } \braket{xy,z} \xmapsto{\mu} (xy)z \in \cM $$
ですので，$\braket{x,y,z}$を$(xy)z$に写します。このことから上記の二つの式が同値であることがわかります。
式\eqref{eq:2}は，式\eqref{eq:1}から$x,y,z \in \cM$を表すブロックを消したものになっています。下側に伸びた3本の線に$x,y,z$のような$\cM$の3個の要素が入力されると捉えると，わかりやすいかもしれません。なお，この図式の左辺は
式\eqref{eq:2}の左辺
のように3個の領域に分けたとき，上側・左下側・右下側の領域がそれぞれ$\mu,~1_\cM,~\mu$を表しています。このため，左辺全体としては$\mu \c (1_\cM \times \mu)$を表しています（$\c$が縦方向の合成で$\times$が横方向の合成に対応しています）。
単位律
また，単位律は次の図式で表されます。
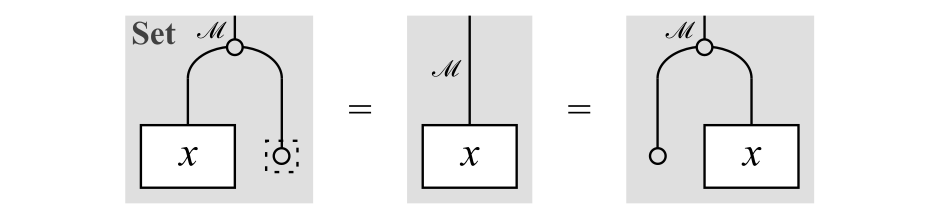単位律
$$\tag{3}\label{eq:3}$$
ただし，補助線で囲まれた丸は単位元$1$を表しています。
写像$\{*\} \ni * \mapsto 1 \in \cM$（ただし，$\{*\}$は要素$*$のみをもつ1点集合）を$\eta$とおくと，この式は次式と同値です。
(2)単位律：$\mu \c (1_\cM \times \eta) = 1_\cM = \mu \c (\eta \times 1_\cM)$
単位律（別表現）
$$\tag{4}\label{eq:4}$$
この図式は，式\eqref{eq:3}から$x \in \cM$を表すブロックを消したものになっています。ただし，式\eqref{eq:2}において$1$を表す丸は，この式では$\eta$を表しています。
モノイド対象
モノイド$\braket{\cM,\cdot,1}$において，集合$\cM$は圏$\Set$の対象とみなせます。集合$\cM$をより一般の圏$\cC$（正確にはモノイダル圏）の対象に拡張し，式\eqref{eq:2}と式\eqref{eq:4}に相当する条件を満たすようなものとして，モノイド対象が考えられます。
モノイダル圏$\braket{\cC,\ot,i}$の対象$a$と射$\mu \colon a \ot a \to a$と射$\eta \colon i \to a$の組が次の二つの条件を満たすとき，モノイド対象とよぶ。
(1)結合律：$\mu \c (1_a \ot \mu) = \mu \c (\mu \ot 1_a)$
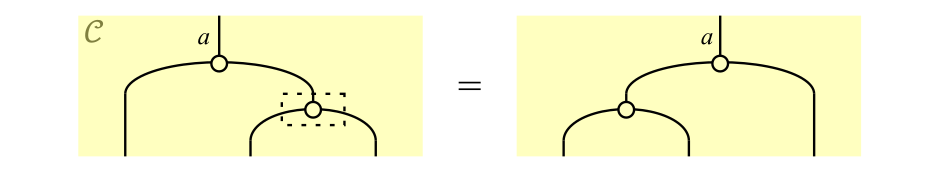結合律
(2)単位律：$\mu \c (1_a \ot \eta) = 1_a = \mu \c (\eta \ot 1_a)$
単位律
なお，線はすべて対象$a$を表している（線のラベル「$a$」は適宜省略している）。
この定義から，モノイド$\braket{\cM,\cdot,1} = \braket{\cM,\mu,\eta}$（ただし$\cdot$を$\mu$とおいて$1$と$\eta$を同一視しています）は，モノイダル圏$\braket{\Set,\times,\{*\}}$におけるモノイド対象であることがわかります。モノイドが満たすべき条件を素直に拡張することで，より一般のモノイダル圏$\braket{\cC,\ot,i}$におけるモノイド対象$\braket{a,\mu,\eta}$が考えられるようになります。
ベクトル空間の圏$\VecK$は，ベクトル空間の直和$\oplus$をモノイド積として0次元ベクトル空間$\{\zero\}$を単位対象とするモノイダル圏とみなせるのでした。ベクトル空間$\V$を任意に選んだとき，$\V$と，$\V$における和$+ \colon \V \oplus \V \ni v \oplus v \mapsto v + v \in \V$と，ゼロベクトル$\zero \in \V$の組$\braket{\V,+,\zero}$は，このモノイダル圏$\braket{\VecK,\oplus,\{\zero\}}$におけるモノイド対象です。結合律は$v + (w + x) = (v + w) + x ~(\forall v,w,x \in \V)$を意味しており，単位律は$v + 0 = v = 0 + v ~(\forall v \in \V)$を意味しています。
モナド
モナドの定義
モナドは，モノイド対象の特別な場合として次のように定義できます。
（モノイダル圏としての）自己関手の圏$\braket{\cC^\cC,\b,1_\cC}$（ 第4回の記事 を参照のこと）のモノイド対象$\braket{T,\mu,\eta}$をモナドとよぶ。
モノイド対象の定義を用いてより直接的な定義に書き換えると，次のようになります。
関手$T \colon \cC \to \cC$と自然変換$\mu \colon T \b T \nto T$（積とよぶ）と自然変換$\eta \colon 1_\cC \nto T$（単位元とよぶ）の組が次の二つの条件を満たすとき，モナドとよぶ。
(1)結合律：$\mu \c (1_T \b \mu) = \mu \c (\mu \b 1_T)$
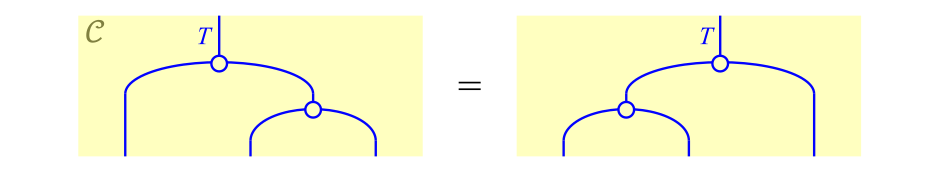結合律
(2)単位律：$\mu \c (1_T \b \eta) = 1_T = \mu \c (\eta \b 1_T)$
単位律
なお，線はすべて関手$T$を表している（線のラベル「$T$」は適宜省略している）。
まとめ
モノイド対象という観点からモナドの定義を紹介しました。圏論では，結合律と単位律というモノイド的な規則がしばしば登場します。この観点では，モナドとはモノイド的な振る舞いをする自己関手のことだといえるかもしれません。次回の記事では，モナドの例を紹介します。
