文献あり

【ストリング図で学ぶ圏論 #9】普遍射と随伴・極限・カン拡張

216

はじめに

今回の記事では，普遍射について紹介します。普遍射を用いると，前回の記事で述べた随伴に加えて極限とカン拡張とよばれる概念を統一的に扱えます。

本連載の目次

#1：圏の定義と具体例
#2：関手と自然変換
#3：垂直合成と水平合成
#4：モノイダル圏
#5：モナドとは自己関手の圏におけるモノイド対象のこと
#6：モナドの例
#7：随伴
#8：関手を表す線の順序の交換
#9：普遍射と随伴・極限・カン拡張（この記事）
#10：ホム関手のストリング図（前編）
#11：ホム関手のストリング図（後編）
#12：米田の補題

普遍射

対象$c \in \cC$と関手$G \colon \cD \to \cC$を任意に選ぶ。ある対象$u \in \cD$とある射$\eta \in \cC(c,Gu)$が存在して，任意の$a \in \cC(c,Gx)$（$x \in \cD$も任意）について

!FORMULA[6][-2028207690][0] $a = G\ol{a} \c \eta$ $$\tag{1}\label{eq:univ}$$

（ただし黒丸は$\eta$）を満たす$\ol{a} \in \cD(u,x)$が一意に存在するとき，組$\braket{u,\eta}$を$c$から$G$への普遍射とよぶ。

式\eqref{eq:univ}を$\braket{u,\eta}$の普遍性とよぶことにします。

補足1：

図式における「$\exists !$」は，そのすぐ右側にあるブロック（今回の場合は$\ol{a}$）が一意に存在するという意味です。なお，その後の「一意に存在する」という文言は冗長ですが，気にしないでください。

補足2：

詳しくは述べませんが，式\eqref{eq:univ}の図式を「上下反転」させたような式を満たすものとして，$G$から$c$への普遍射も同様に定義できます。

随伴

普遍射と随伴には次のような関係があることが知られています（拙著Nak-2025で証明しています）。

関手$G \colon \cD \to \cC$が各$c \in \cC$について$c$から$G$への普遍射$\braket{u_c,\eta_c}$をもつと仮定する。このとき，$Fc = u_c$ $~(\forall c \in \cC)$を満たし，$\eta \coloneqq \{ \eta_c \}_{c \in \cC}$が単位であるような随伴$\braket{F,G,\eta,\varepsilon}$が一意に存在する。

式\eqref{eq:univ}より，普遍射$\braket{u_c,\eta_c}$は次式のように表せます（ただし黒丸は$\eta_c$）。

!FORMULA[29][1034219598][0]の普遍性 $\braket{u_c,\eta_c}$の普遍性 $$\tag{2}\label{eq:univ_adj}$$

前回の記事で導入した単位$\eta$の表記を用いれば，普遍射$\braket{u_c,\eta_c}$は次式で表されます（なお，$Fc = u_c$です）。

単位!FORMULA[34][1118736778][0]を用いた普遍射!FORMULA[35][1034219598][0]の表記単位$\eta$を用いた普遍射$\braket{u_c,\eta_c}$の表記 $$\tag{3}\label{eq:adj}$$

補足1：

この命題により得られる関手$F$と自然変換$\eta$を用いて随伴を定義することも可能です。この定義は第7回の記事で述べた随伴の定義と同値であることが知られています。

補足2：

ここでは$G$の左随伴が普遍射を与えることを述べましたが，式\eqref{eq:univ_adj}の図式を「上下反転」させれば$F$の右随伴が普遍射を与えることを示せます。

（余）極限

関手圏$\Func{\cJ}{\cC}$を考えます。$D \in \Func{\cJ}{\cC}$から対角関手$\Delta_\cJ \colon \cC \to \Func{\cJ}{\cC}$への普遍射を，$D$の余極限とよびます。ただし，$\Delta_\cJ \coloneqq \Endash \b {!}$です（第8回の記事で述べました）。具体的には，任意の$\alpha \in \Func{\cJ}{\cC}(D,\Delta_\cJ c)$（$c \in \cC$も任意）について

!FORMULA[48][-190502657][0]の普遍性 $\braket{d,\eta}$の普遍性 $$\tag{4}\label{eq:univ_colim}$$

（ただし黒丸を$\eta$とおく）を満たす$\ol{\alpha} \in \cC(d,x)$が一意に存在するとき，組$\braket{d,\eta}$が$D$の余極限です。この図式が式\eqref{eq:univ}に対応しています。第8回の記事で述べたような線の入れ替えを行うと，式\eqref{eq:univ_colim}は次式のようにも表せます。

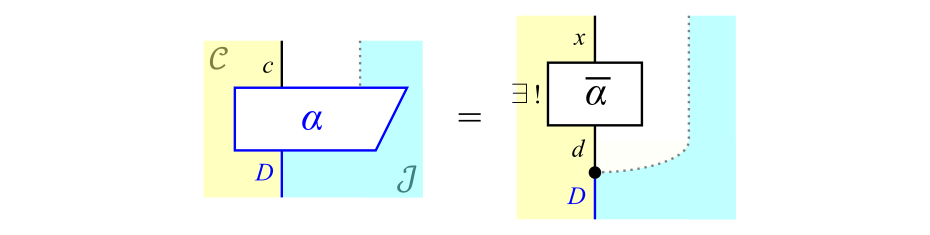$式\eqref{eq:univ_colim}の別表記$ 式\eqref{eq:univ_colim}の別表記

とくに随伴と普遍射との関係を用いると，$\cJ$から$\cC$への任意の関手が余極限をもつことは，対角関手$\Delta_\cJ$の左随伴（$\colim$と書きます）が存在することと同値であることを示せます（証明は割愛します）。このような随伴があるとき，式\eqref{eq:adj}と同様に$D$の余極限は次式のようにも表せます。

!FORMULA[59][36740][0]の余極限!FORMULA[60][-190502657][0] $D$の余極限$\braket{d,\eta}$

ここで，$\colim D = d$を満たすように関手$\colim$を選べます。

補足：

余極限と同様に，式\eqref{eq:univ_colim}の図式を「上下反転」させれば$D$の極限を定義できます。

カン拡張

2個の関手$K \colon \cC \to \cD$と$F \colon \cC \to \cE$を考えます。$F \in \Func{\cC}{\cE}$から$\Endash \b K \colon \Func{\cD}{\cE} \to \Func{\cC}{\cE}$への普遍射を，$K$に沿った$F$の左カン拡張とよびます。具体的には，任意の$\alpha \in \cC(F,H \b K)$（$H \colon \cD \to \cE$も任意）について

!FORMULA[72][931722263][0]の普遍性 $\braket{L,\eta}$の普遍性 $$\tag{5}\label{eq:univ_Kan}$$

（ただし黒丸を$\eta$とおきます）を満たす$\ol{\alpha} \in \cC(L,H)$が一意に存在するとき，組$\braket{L,\eta}$が$K$に沿った$F$の左カン拡張です。この図式が式\eqref{eq:univ}に対応しています。余極限の場合と同様に線の入れ替えを行うと，式\eqref{eq:univ_Kan}の別表記として次式が得られます。

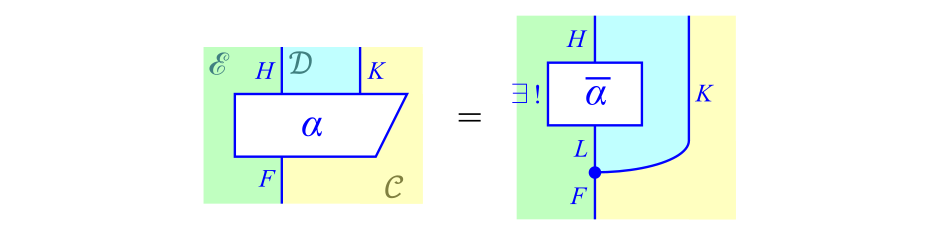$式\eqref{eq:univ_Kan}の別表記$ 式\eqref{eq:univ_Kan}の別表記

とくに随伴と普遍射との関係を用いると，任意の$F \colon \cC \to \cE$について$K$に沿った$F$の左カン拡張が存在することは，関手$\Endash \b K$の左随伴（$\Lan_K$と書きます）が存在することと同値であることを示せます（証明は割愛します）。このような随伴があるとき，式\eqref{eq:adj}と同様に$K$に沿った$F$のカン拡張は次式のようにも表せます。

!FORMULA[86][36957][0]に沿った!FORMULA[87][36802][0]の左カン拡張!FORMULA[88][931722263][0] $K$に沿った$F$の左カン拡張$\braket{L,\eta}$